巧借平几知识 优化解几运算

张玉红

(浙江省桐庐富春高级中学，311500)



巧借平几知识优化解几运算

张玉红

(浙江省桐庐富春高级中学，311500)

高考中有些解析几何问题, 若用坐标思想选择代数方法解答,往往思路清晰，但运算量大，难以进行到底.若从平面几何的角度来审视, 分析题中几何量之间的关系,认清问题的本质,挖掘其中隐含的平面几何背景,合理转化,往往会化难为易,收到出奇制胜的效果．现以各地高考试题为例加以说明,以期对同学们有所帮助．

一、利用两点之间线段最短求解

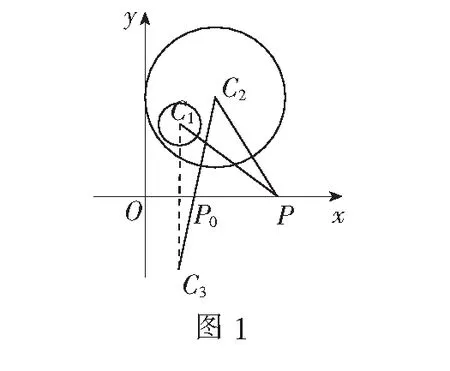
例1(2013年重庆卷)已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1和圆C2上的动点,P是在x轴上的动点,则|PM|+|PN|的最小值为()

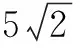
二、利用直角三角形和等腰三角形的性质求解

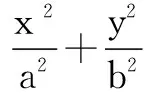
三、利用平行线分线段成比例定理求解

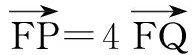
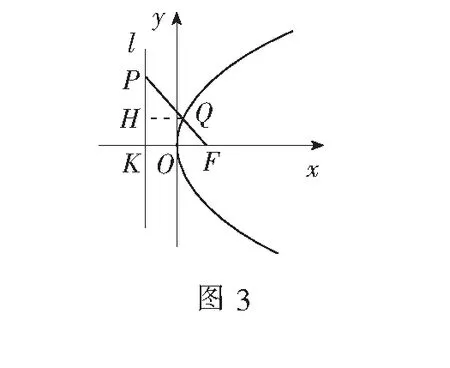
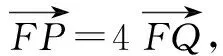
四、利用三点共线求解

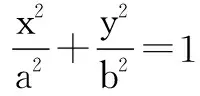
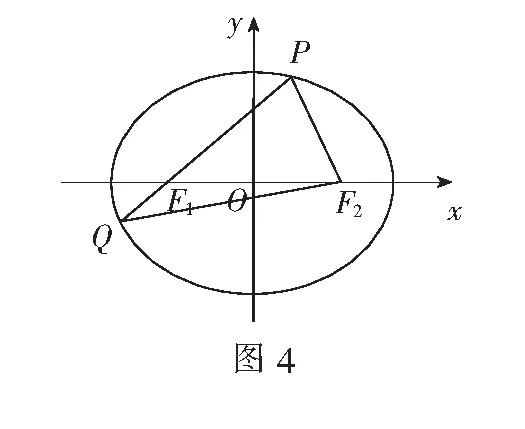
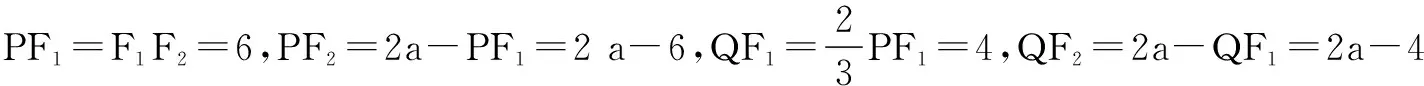
五、利用内角平分线定理求解

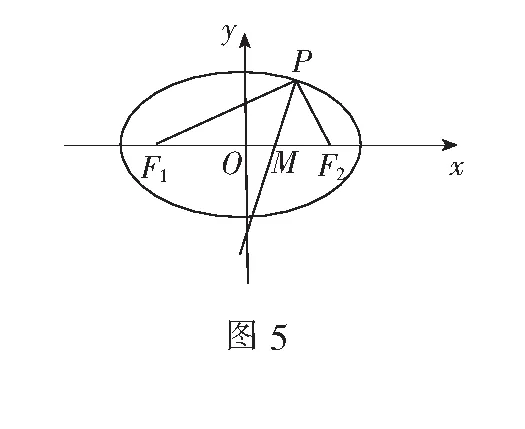
(1)求椭圆C的方程；

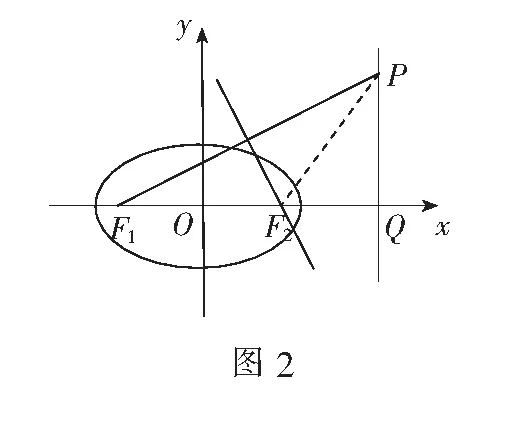
(2)点P是椭圆C上除去长轴端点外的任意一点,联结PF1,PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围.

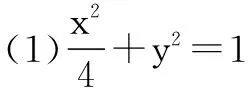
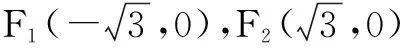
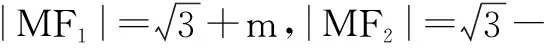
∵PM平分∠F1PF2,

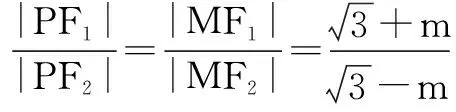
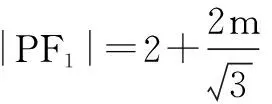
六、利用三角形中位线定理求解

例6(2009年全国卷)已知直线y=k(x+2)(其中k>0)与抛物线C:y2=8x相交于点A,B,点F为抛物线C的焦点,若|FA|=2|FB|，试求k的值.

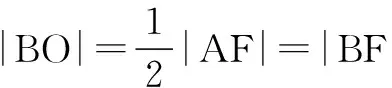
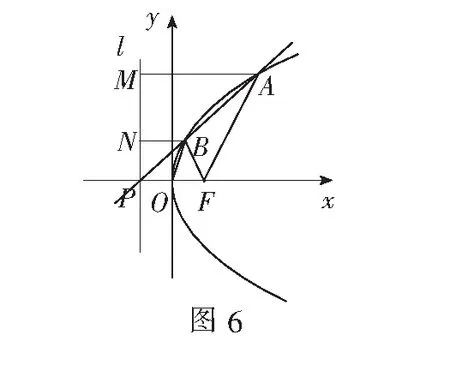
七、利用圆的性质求解

(1)求椭圆的离心率；

(2)求直线AB斜率；

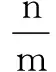
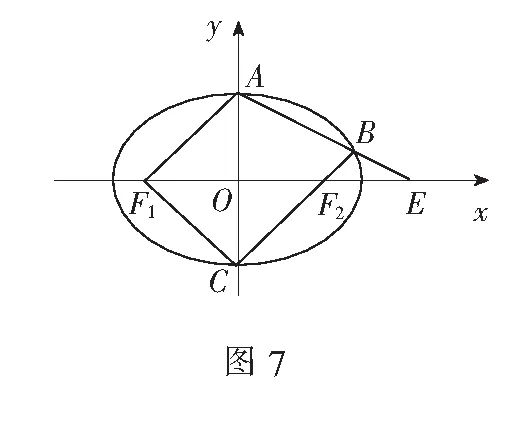
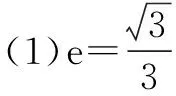
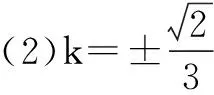
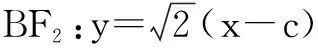
八、利用三角形相似性质求解

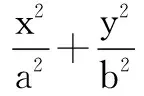
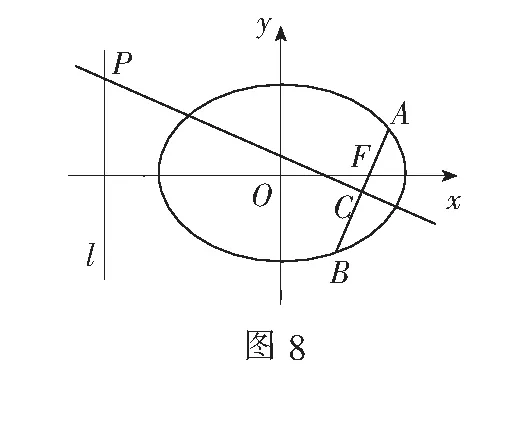
(1)求椭圆的标准方程.

(2)过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.

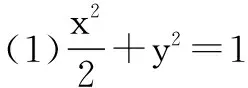
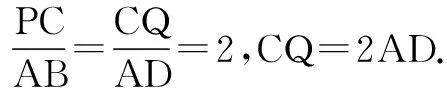
从以上例题的分析与解答不难看出:在处理解析几何问题时,充分利用图形的几何特征和曲线自身特点,结合平面几何知识,就可避开繁难的代数运算,达到简洁求解的目的．

○解题思路与方法○