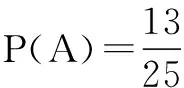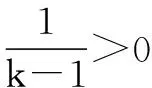浅议概率问题的常见错误

周文国

(江苏省张家港中等专业学校，215600)



○学习指导○

浅议概率问题的常见错误

周文国

(江苏省张家港中等专业学校，215600)

要学好概率，首先必须准确理解和把握概率论的有关概念，掌握其本质内涵，否则会产生这样或那样的种种错误.兹分类例说如下.

类型1不能区分 “非等可能”与“等可能”

例1抛掷两枚骰子,求所得的点数之和为6的概率.

错解抛掷两枚骰子,出现的点数之和为2,3,4,…12共11种基本事件,故所求概率

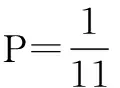
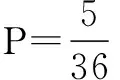
类型2不能区分“互斥”与“对立”

例2把红、黑、白、蓝4张纸张牌随机分给甲、乙、丙、丁4个人,每个人分得1张,事件“甲分得红牌”与“乙分得红牌”是______事件.

错解对立事件.

分析本题错误在于把“互斥”与“对立”混同.要准确解答这类问题,则需要弄清楚对立事件与互斥事件的联系与区别:(1)两个事件互斥只表明这两个事件不能同时发生,即至多只能发生其中一个,但可以都不发生,而两事件对立表示它们有且只有一个发生；(2)两事件对立,必定互斥,但互斥未必对立;(3)互斥的概念适用于多个事件,但对立概念只适用于两个事件.

正解事件“甲分得红牌”与“乙分得红牌”是不能同时发生的两个事件,这两个事件可能恰好有一个发生,也可能两个都不发生,因此它们为互斥但不对立事件.

类型3不能区分“互斥”与“独立”

例3甲投篮命中率为80%,乙投篮命中率为70%,每人投篮3次,两人都恰好命中2次的概率是多少?

错解设“甲恰好投中两次”为事件A,“乙恰好投中两次”为事件B,则所求事件为A+B,且

P(A+B)=P(A)+P(B)

=C23×0.8×0.2

+C23×0.72×0.3

=0.825.

分析事件A、B是独立事件.互不影响，可同时发生，因而它们不互斥.本题错误的原因是把相互独立事件同时发生的事件当成了互斥事件.

正解设“甲恰好投中两次”为事件A,“乙恰好投中两次”为事件B,且A、B相互独立,则两人都恰好投中两次为事件A·B,于是

P(A·B)=P(A)·P(B)

=C23(0.82×0.2+0.72×0.3)

=0.169.

类型4混淆“条件概率”与“积事件的概率”

例4袋子中有6个黄色,4个白色的乒乓球,作不放回抽样,每次任意取一球,取两次,求第二次才能取到黄色球的概率.

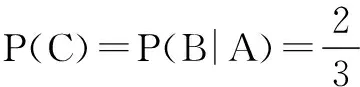
分析本题的错误在于没有弄清楚P(B|A)与P(AB)的含义.P(AB)表示在样本空间S中,A与B同时发生的概率,而P(B|A)表示在缩减的样本空间中,作为条件的A已经发生的条件下事件B发生的概率.

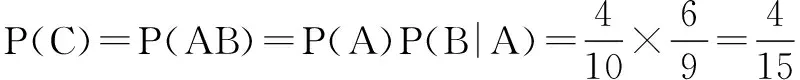
类型5不能区分“有序”与“无序”

例5从10件产品(其中3件次品)中,一件一件地不放回任意取4件,求4件中恰有1件次品的概率.

分析该题错在计算所有等可能结果的个数是用排列的方法,即考虑了抽取的顺序,而计算事件A所包含结果个数时用组合的方法,即没有考虑抽取的顺序.

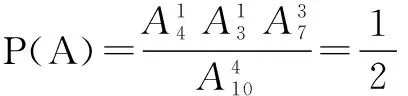
正解2从组合的角度考察问题，有

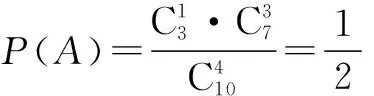
类型6忽视 “无放回抽取”与“有放回抽取”

例6从含有2件正品a1、a2和一件次品b的的三件产品中每次任意抽取一件,每次取出后不放回,连续取2次,记“取出的两件中恰好有一件次品”为事件A；如果将“每次取出后不放回”换成“每次取出后放回”,连续取2次,记“取出的两件中恰有一件次品”为事件B,求P(A)与P(B).

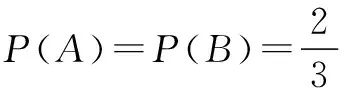
分析本题错在混淆“每次取出后不放回”与“每次取出来后放回”，其样本空间有很大不同.从3件产品中不放回地抽取2件和有放回抽取2件的基本事件都不是很大,可以一一列举出来.

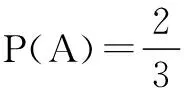
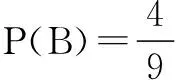
类型7忽视古典概型的有限性

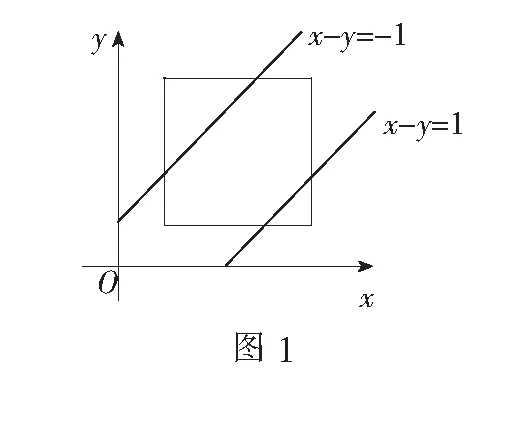
例7甲、乙两人玩数字游戏,先由两人在心中各想一个整数,分别记为x、y,且x、y∈[1,5],若|x-y|≤1,则称甲、乙两人“心有灵犀”,求甲、乙二人“心有灵犀”的概率.

错解设甲、乙二人“心有灵犀”为事件A,由于x、y∈[1,5],且|x-y|≤1,如图1,由几何概型得到概率公式,得

.

分析本题没有注意x、y的取值是整数,忽视了古典概型的有限性.