一道高考题求解视角探索
2016-06-12张艳宗马喜君
张艳宗 马喜君
(浙江省海盐元济高级中学,314300)
一道高考题求解视角探索
张艳宗马喜君
(浙江省海盐元济高级中学,314300)
一、试题呈现
(2015年浙江高考题)若实数x,y满足x2+y2≤1,则|2x+y-2|+|6-x-3y|的最小值为______.
二、试题解析
这是2015年浙江省高考数学理科卷的第14题,问题要求的是在约束条件(实数x,y满足x2+y2≤1)下,以x,y为变量的二元函数(|2x+y-2|+|6-x-3y|)的最小值.问题将绝对值和函数最值问题结合起来,题干新颖,表述简洁,背景深刻,命题方法不落俗套.由于此题涉及二元函数的最值,且又有绝对值做“伪装”,很多学生考后反映求解此题时无从下手,而且平时老师所教的求函数最值的方法在考场上又用不上,因此,此题成为了学生高考中的一只“拦路虎”.那么这个试题到底难在何处?如何突破?我们通过分析试题的特点,探索了求解这个问题的四个视角,希望给教师的教和学生的学带来有益的启发.
三、试题解决的视角
为了行文方便,设F=|2x+y-2|+|6-x-3y|.
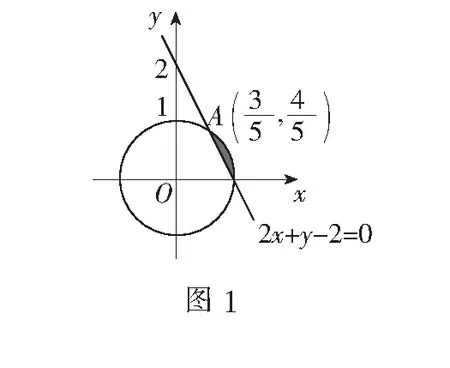
方法1如图1,直线l:2x+y-2=0将单位圆面x2+y2≤1分为两部分:
(1)当2x+y-2>0时,F=|2x+y-2|+|6-x-3y|=x-2y+4,问题转化为求目标函数z=x-2y+4在阴影区域及其边界上的最小值.由线性规划知识可求得F>3.
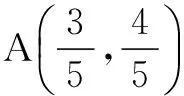
评注这种解法的最初想法在于去掉绝对值,而这是碰到绝对值问题时最容易想到的一种思考方法,思路比较自然.如果我们注意到这种解法中等号成立的条件,那么我们还可以有下面更简单的解法.
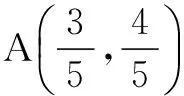
评注这种解法之所以成功的前提在于我们知道F取最小值时,点(x,y)必在直线2x+y-2=0上.
2.不等式视角
分析最值问题尤其是含绝对值的最值问题通常可以借助绝对值不等式的性质、柯西不等式等重要不等式进行求解.在求解时,要注意取到最值时的条件.
方法1对于任意实数a,b,|a|+|b|≥|a+b|,当且仅当ab≥0取等号;|a|+|b|≥|a-b|,当且仅当ab≤0取等号.因此,我们有:
(1)当x2+y2≤1时,易知6-x-3y>0;当2x+y-2>0时,
F≥|(2x+y-2)+(6-x-3y)|
=|x-2y+4|.
①
由于x2+y2≤1,不妨令x=rcosθ,y=rsinθ,其中0≤r≤1,0≤θ≤2π,则
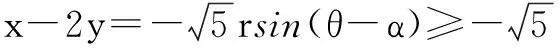
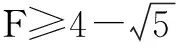
(※)
(2)当2x+y-2≤0时,F≥|(2x+y-2)-(6-x-3y)|=|3x+4y-8|.
②
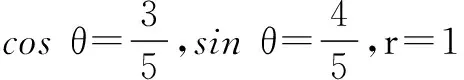
评注利用绝对值不等式减少绝对值个数也是解决此类问题时的一种常规方法,在选用|a|+|b|≥|a+b|还是|a|+|b|≥|a-b|需要分别讨论;此外还要注意使用绝对值不等式时的取等号条件.在求解① 、② 的最小值时,由x2+y2≤1的条件进行三角代换,是非常自然的思路,但求解时易忽视对2x+y-2>0时F>3的证明.
方法2由上面的分析可知,我们只需求当2x+y-2≤0时,F=8-3x-4y的最小值.为了避免三角代换,结合约束条件x2+y2≤1,我们可以利用待定系数法,借助基本不等式进行凑配,求得F的最小值.由基本不等式,我们有x2+a2≥2ax,y2+b2≥2bx(这里a,b是待定的正常数),从而
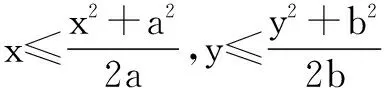
因此,F=8-3x-4y
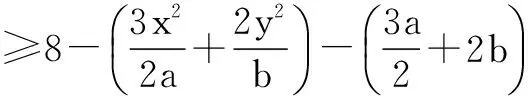
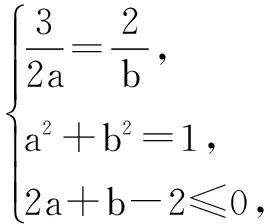
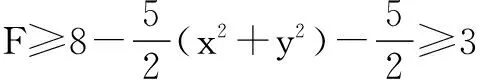
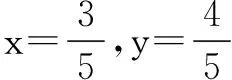
评注此处通过待定系数法使用基本不等式,实现了把自变量从一次到二次的转化(即向已知条件靠拢).另辟蹊径,给人以美的享受,也是学生容易掌握的一种方法.
方法3为了求当2x+y-2≤0时,F=8-(3x+4y)的最小值,由x2+y2≤1,我们可以直接利用柯西不等式进行解决.由柯西不等式我们有
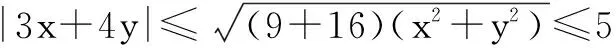
即3x+4y≤5,所以F≥3.由式② 及柯西不等式取等号条件,当且仅当
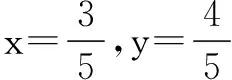
评注在② 式的最小值的求解过程中,利用柯西不等式建立了x,y的一次式与x,y的二次式之间的不等关系,与前面的三角代换相比,柯西不等式更直接、简洁、巧妙.
3.函数与方程视角
分析在处理多元变量最值问题时,可将函数看成是某一变量的函数,其他字母视为参数,利用函数的单调性、最值等性质逐个减少变量,达到“消元”的目的.另外,“代入消元”也是一种常见的消元方式.因此,求当2x+y-2≤0时,F=8-3x-4y的最小值,我们还有如下的思考途径:
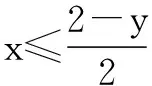
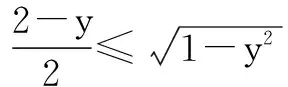
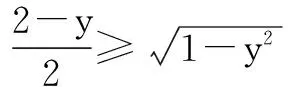
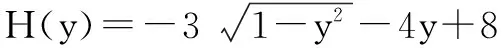
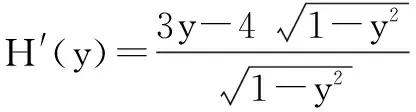
当-1≤y≤0时,H′(y)<0,H(y)在[-1,0]上递减;
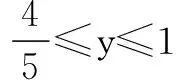
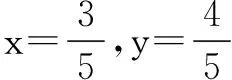
评注将多元函数的最值问题转化为一元函数的最值问题,借助不等关系转化,体现了转化与化归的思想在解题中的应用.
评注通过代入消元,建立了关于d的不等关系,体现了函数与方程的思想.由不等式有解的必要条件我们得到了判别式大于等于0,所以,在求出d的最小之后需要进行检验.
4.解析几何视角
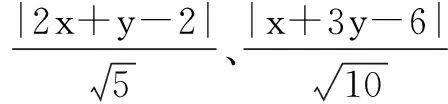
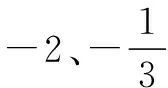
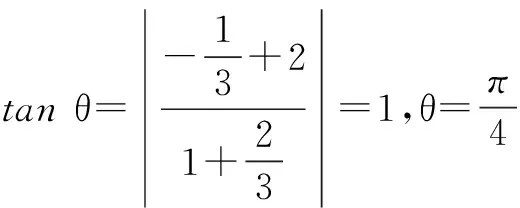
令点P(x,y)是x2+y2≤1所表示区域上的一点,PN⊥l1,PM⊥l2,则
F=|2x+y-2|+|6-x-3y|
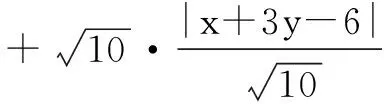
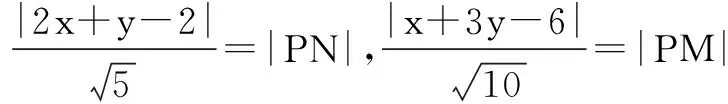
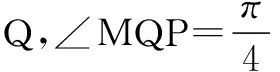
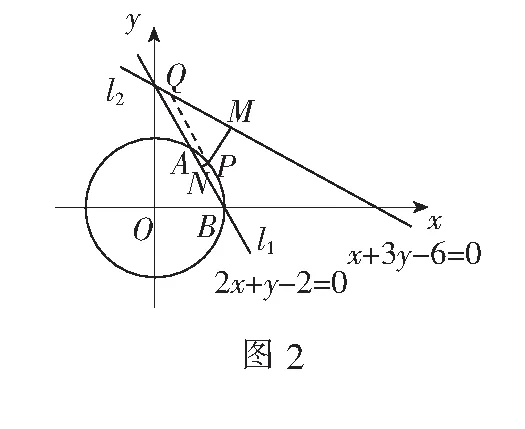
评注从上面的解法我们可以看出,此题的几何背景即圆盘上一点到两条直线的距离和.