关于“导数在研究函数中的应用—单调性”的教材比较及教学改进

樊　蓉

(江苏省扬州中学,225002)



○教学研究○

关于“导数在研究函数中的应用
—单调性”的教材比较及教学改进

樊蓉

(江苏省扬州中学,225002)

前不久,笔者参加了2015年本市高中数学优质课比赛.参赛的内容是“导数在研究函数中的应用——单调性”的第一节课.现谈谈对这节课的的教材比较和教学改进的一点拙见,以期抛砖引玉.

一、教材比较，同课异构

1.人教版A版选修2-2中1.3.1函数的单调性与导数

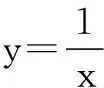
2.北师大版选修2-2中1.1导数与函数的单调性

① 问题提出:从导数f ′(x)和函数的单调性都是刻画函数的变化的共性中直接提出问题:导数与函数的单调性之间有何关系?② 实例分析:研究一次函数、指数函数、对数函数、二次函数的导数及其单调性；③ 抽象概括:导函数的符号与函数的单调性之间的关系.

3.湘教版选修2-2中4.3.1利用导数研究函数的单调性

4.苏教版选修2-2中1.3.1单调性

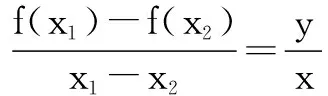
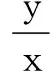
二、教学改进，提升效果

由于高中学生知识的局限性,导数和函数单调性的关系不能加以严格证明.为了让学生能够形成完整的认知结构,各版本教材在立足各自的教学侧重点和保证前后知识的连贯性的基础上,处理本节内容的方式各有特色.但笔者认为，从学生的角度出发,还有两个不容忽视的地方需要完善:第一,在引入课题环节中,基于学生在高一已经学习过如何判断函数的单调性,那现在为什么还要再用导数来研究函数的单调性?第二,在探究新知环节中,本节课基于教材内容的限制,对导数和函数的单调性的关系只能通过几何直观探索,但是如何能自然地、不生硬地过渡到几何的直观探索上呢?下面，笔者在分析各版本教材的基础上,对本节上述两点在引入课题和探究新知这两个环节上用一系列的问题串作了一个教学设计的改进.

1.引入课题

问题1通过前面对导数的学习,我们知道导数作为函数的变化率刻画了函数变化的趋势(上升或下降),那么联系函数的性质想一想还有什么也可以用来刻画函数变化趋势?(单调性)

问题2过去我们怎么判断函数单调性?(图象法、定义法)

学生活动1试讨论函数f(x)=x-lnx的单调性.

设计意图笔者通过设计一个用函数单调性定义不能解决的问题,来吸引学生注意力的同时,可以不知不觉地引导学生按照既定目标,追求新知识.

教学启示现代认知心理学认为:思维的本质在于问题的情境,恰当的问题情境不但可以激发学生的学习兴趣,启发学生的思维,更重要的是能让学生学会如何思考和学习.所以，教师应密切联系学情,结合学生的认知特点,精心创设问题情境,营造思考的氛围,激发学生探求新知的欲望和动机.

2.探究新知

在图象法和定义法实施都比较困难的情况下,寻求其他方法.

问题3用定义判断单调性时,对任意x1，x2∈I,x1

这种形式看成斜率说明什么?

说明函数在该区间上单调递增时,该区间上任意两点连成的割线的斜率恒为正，反之也成立.

问题4割线的斜率可以反映曲线的平均变化趋势,当其中一点无限逼近另一点时,割线就成了该点处的切线.切线的斜率反映的是曲线的瞬时变化趋势.若该点处切线的斜率为正或负,从图象变化趋势上看说明什么?

说明函数在该点处呈上升或下降的趋势.

如果函数在区间(a,b)内的每一点处的变化趋势都相同,那么函数在该区间上整体变化趋势如何,单调性又如何呢?

学生活动2利用多媒体动画观察函数y=x2的图象,研究每一点处切线的斜率与单调性的关系.

以函数y=x2图象为例,定义域为R,在区间(-∞,0)内任一点处的切线斜率为负,每一点处的变化趋势保持一致,都是下降趋势,故函数图象呈下降趋势,函数单调递减;在x=0处的切线斜率为0(要提醒学生不研究某一点处的单调性,但若在区间(a,b)内每一点处的切线斜率为0,如常值函数,则无单调性);在区间(0,+∞)内任一点处的切线斜率为正,每一点处的变化趋势保持一致,都是上升趋势,故函数图象呈上升趋势,函数单调递增.

若函数在区间(a,b)内的的每一点处呈上升(下降)趋势,则函数图象整体呈上升(下降)趋势,函数单调递增(减).由此可见，在区间(a,b)内的切线的斜率决定了函数的图象变化趋势,也就是函数的单调性.即函数在区间(a,b)内的每一点处的切线的斜率大于零,函数单调递增;在区间(a,b)内的每一点处的切线的斜率小于零,函数单调递减.

而导数的几何意义就是切线的斜率.

所以一般地,对于可导函数y=f(x),x∈(a,b),如果f ′(x)>0,那么f(x)为该区间上的增函数;如果f ′(x)<0,那么f(x)为该区间上的减函数.

问题5在区间(a,b)内,若函数f(x)是增函数,能否推出f ′(x)>0?

不能.函数f(x)=x3在区间R上单调增,但是f ′(x)=3x2≥0,其中f ′(0)=0，所以f ′(x)>0是函数单调增的充分不必要条件.进而若函数f(x)在区间(a,b)内是增函数，则f ′(x)≥0,且f ′(x)在区间(a,b)的任意子区间上都不恒为0.

设计意图从学生实际出发,遵循最近发展区原理,应充分利用学生已有的知识储备，不能生搬硬套.笔者首先利用函数的单调性的定义,加以变形,让学生联系到割线的斜率,再由逼近的思想,转化为研究切线的斜率,由切线的斜率引申为研究函数的单调性，最后得出导数与函数的单调性的关系.

教学启示皮亚杰强调:“教师的工作不是教给学生什么,而是努力构建学生的知识结构,并用种种方法来刺激学生的欲望,这样,学习对于学生就是一个主动参与的过程了.”每节课上都有阻挡学生自学自懂的“结”，一个真正有责任感的教师,不应刻意去示范自己完美打开这个“结”的过程,而应从学生的角度出发,引导学生自主探索,自己解“结”,最终获得知识、增长解决问题的能力、提升思维水平.

在新课程的背景下,利用教材的最高境界是“得其意,忘其形”.要想提高课堂效率,提升教学品质,这就需要我们在备课时钻研教材,比较教材,博采众长,多交流,多反思.从学生已有的认识经验和思维水平出发,顺应学生的认知习惯和认知方式,设计适合学生的教学形式,构建生动有效的数学课堂.

教参中指出本节课的教学目标是:借助几何直观探索并了解函数的单调性；通过初等方法与导数方法在研究函数性质过程中的比较,体会导数方法在研究函数性质中的一般性和有效性,同时让学生感受和体会数学自身发展的一般规律.但是在以往的课堂教学过程中,我们往往单纯追求训练学生运用导数来研究函数的单调性,没有重视为什么要用导数来研究函数的单调性,忽略了学生的心理状态,使得用导数研究函数的单调性缺乏主观愿望上的心理需求,造成被动式的接受.为此，笔者在备课的过程中查阅了不同版本教材对这节课教学的设计,感受“同课异构”的魅力,力求能将利用导数来研究单调性的缘由挖掘得更加深入,能充分调动学生的积极性,将课堂效率最大化.