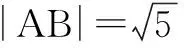“圆”来如此精彩

江志杰

(福建省惠安第三中学，362100)



“圆”来如此精彩

江志杰

(福建省惠安第三中学，362100)

本文拟通过一些典型例子,谈谈构建圆辅助解题的若干途径，以供读者参考.

一、紧扣圆的基本定义

我们知道,平面内到定点(圆心)的距离等于定长(半径)的点的轨迹是圆,因此有关涉及定点、定长或等长的问题往往可以构造辅助圆来解决.

例1平面内向量a,b,c满足|a|=|b|=2,|c|=1,(a-c)·(b-c)=0,求|a-b|的取值范围.

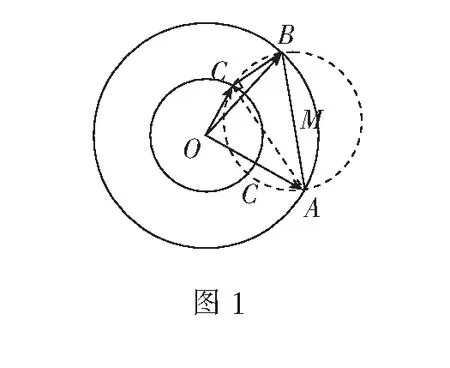
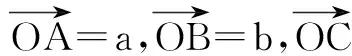
这里值得一提的是圆还有另外一种“定义”——阿波罗尼斯圆的定义:平面内到两个不同定点A,B的距离之比为常数λ(λ≠1)的点的轨迹是圆(若λ=1,则点的轨迹是线段AB的中垂线).这种圆的“定义”在教材习题中有涉及,但并未引起大家注意和重视,因而对符合该定义条件的点的轨迹，很多人往往不知道联想起圆，请见下例.

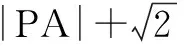
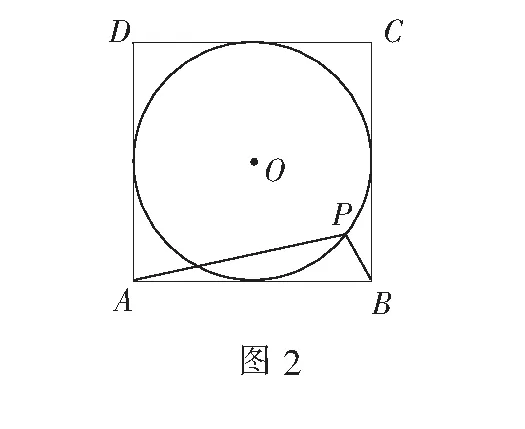
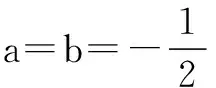
如图3，可得

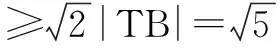
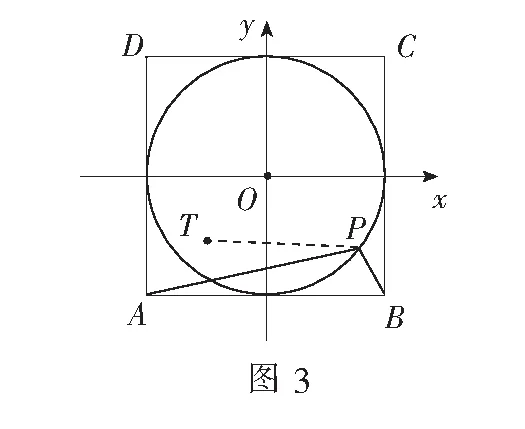
评注上述解析其实是逆用圆的阿波罗尼斯定义,找到圆内符合相关条件的定点,从而实现问题的化解.

二、抓住垂直的典型特性

例3已知实数a,b,c成等差数列(a,b不全为零),点A(0,-3)在直线ax+by+c=0上的射影为点M(如图4),若点N(2,3),则|MN|的最大值为______.

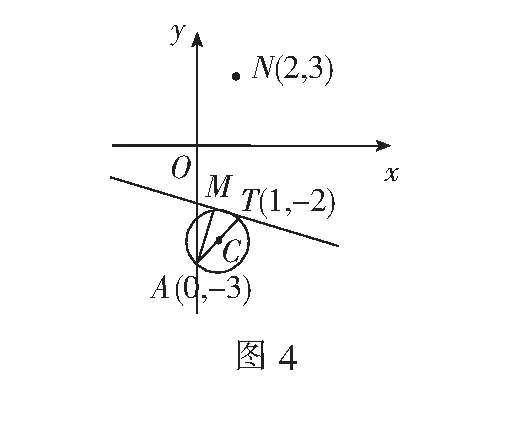
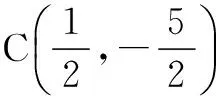
三、利用直线与圆的位置关系

我们知道,当圆心C到直线l的距离d分别满足:d>r、d=r和d

例4在坐标平面内与点A(1,2)距离为1,且与点B(3,,1,)距离为2的直线共有______条.

四、创设圆周角定理的运用情境

在圆中,同弧所对的圆周角相等，据此说明,若三角形的某边及其对角确定,则该边所对的顶点必在其外接圆上运动.

例6在∆ABC中,若∠A=60°,BC=2,则∆ABC的面积的最大值为______.

五、配凑圆方程的形式结构

圆的方程是关于变量x,y的二元二次方程形式(不含xy的项),且x2,y2的系数相同.某些高中数学问题中的等量关系经过适当变形配凑后,往往具备了圆的方程结构,于是自然地运用圆的有关知识找到化解问题的途径.

例9在区间[0,π]上,求函数f(x)=3cosx+2-|3sinx-1|的零点个数.

构造辅助圆解题是数形结合、转化化归思想的强烈展现,它将抽象复杂的数学问题形象化、具体化,解答过程极具数学魅力,超凡脱俗的解法总能给人清新别致的美感.当然,其关键还是要求我们善于捕捉隐含于问题中与圆有关的信息,把握问题的本质特征,方能拓宽解题思路和思维空间.