高中数学解题教学中的“度”与“悟”
2016-05-14吴健
吴健
摘要:解题教学是高中数学教学的重要内容,是培养学生分析、思维、计算能力的主要途径。讲与练是解题教学的两个有效手段,懂与会是教学目标的两个层次,尽管“教之道在于度,学之道在于悟”是人尽皆知的至理名言,但如何把握讲与练之“度”?怎样达成懂与会之“悟”?这两个问题却着实难住了不少师生,且看本文作者有何见解。
关键词:解题教学;讲与练;懂与会;一题多解;解题反思
中图分类号:G633.6 文献标识码:A 文章编号:1992-7711(2016)05-075-2
如果说“问题”是数学的心脏,那么“解题”就是数学的灵魂。解题教学自然是数学教学中最重要的内容之一。教之道在于度,学之道在于悟。章建跃先生在《数学教育心理学》中指出“有效教学的精髓应是培养学生的数学悟性”,然而在平时的教学中,如何把握教之“度”,从而促进学之“悟”已然成为许多老师纠结的一项课题,本文就这一问题谈谈个人的一丝看法。
一、讲与练之“度”
讲与练是解题教学的双翼。毫无疑问,解题教学中教师需要做“慢镜头”式的示范和讲解,学生则需要在思维的参与下顺畅听懂,在及时的练习中加以模仿,在不断的模仿中逐渐理解,在理解的基础上熟练运用,在运用的过程中领悟本质。这就是我们常说的“精讲多练”的内涵。至于具体到一堂课,究竟讲多长时间、练多长时间,不好一概而论。一般而言,学生基础差、能力弱的,课堂上可能就要多讲一点,反之则可以少讲一点。同样的道理,困难的问题课堂上要多讲一点,容易的问题课堂上就少讲一点;知识方法形成阶段多讲一点,巩固阶段就少讲一点。讲的最低要求是学生能够“听懂”,衡量是否“听懂”的标准是会不会“模仿”,这也是“练”的前提条件。
讲的关键在于解剖、暴露解法形成的思维过程,而不只是充当一个“熟练的演绎者”呈现完整的解题过程。
波利亚在“怎样解题表”中给出了一个宏观解题程序:弄清问题、拟定计划、执行计划、检查答案。具体地,我们可以把解题过程分解为以下的一串问题:
①它是一个什么范畴的问题?要解决什么问题?即“目标”是什么?
②现有哪些材料(条件)?有没有“潜在”的、“隐含”的条件?从题目的叙述中获取“符号信息”,从题目的图形中获取“形象信息”等。
③有哪些工具?条件与结论之间有什么联系?从已经学过的相关概念、定理、公式、基本模式和解题经验中提取。
④还缺少(需要)什么?能否以现有的条件,在工具的助推下满足这个需求?
⑤在相关工具的作用下,从条件到结论,是否形成了一个和谐、缜密的逻辑结构?
⑥结论是否完备、纯粹?
上述过程的顺利实施既需要充分的知识储备、基本的经验积累,也需要丰富的联想、机智的策略。
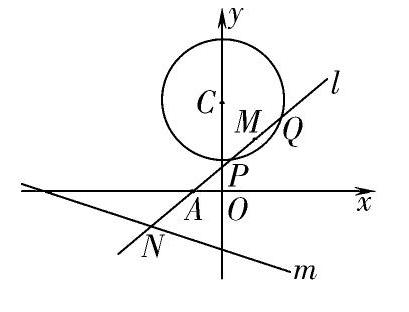
例1 已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于P、Q两点,M是PQ中点,l与直线m:x+3y+6=0相交于N,求AM·AN的值。
讲解:
Q1:这是一个什么问题?——解析几何中的“直线和圆”的位置关系。
Q2:解析几何的本质是什么?——借助坐标系,用代数的方法解决几何问题。
Q3:“直线和圆”的位置关系中最关键的量是什么?——圆心到直线的距离。
Q4:本题要解决什么问题?——起点相同、方向相反的两个向量的数量积。
Q5:求两个向量的数量积有哪些办法?——a·b=|a|·|b|·cos
Q6:本题宜选择哪个办法?——注意到在平面直角坐标系中,A点的坐标已知,只要求出M,N两点的坐标,即可用坐标运算求AM·AN。
Q7:本题还有哪些条件?M,N两点的坐标是否可求?怎么求?——注意到N点是直线l,m的交点,而直线m的方程已知,只需有直线l的方程,即可通过解方程组求得N点坐标,又直线l过点A,故可以设直线l的斜率(关注斜率不存在的情况)。M点是直线l被椭圆截得的弦的中点,在有直线l方程的条件下,可以通过解方程组,结合韦达定理求出M点坐标。
Q8:是否可以顺利实施?——
讲解题,追求的是方法形成的过程顺理成章、自然流畅,学生感同身受、跃跃欲试;而不是显示老师的功力神奇,总有巧妙的方法横空出世,让学生心悦诚服、顶礼膜拜,然后再进行牵强附会的解释、一招一式的归类。讲解题,就是引导学生奔着目标有序前进。
二、懂与会之“悟”
“上课听起来全懂,自己做的时候不会”是数学学习中普遍存在的现象,困扰着很多学生和家长,甚至也困扰着部分教师。这其中可能有老师讲的原因,即所谓讲的不得法、不到位,但更重要的原因是“懂”和“会”根本就是学习过程中的两个相距遥远的阶段,一个是学习的起点,一个是学习的终点,其间隔着几乎全部的学习过程,这个过程就是“悟”。所谓“悟”一定不是老师讲了几道例题之后跟学生说“你们去悟吧”这么简单。“悟”是在听懂的基础之上,在练习中模仿、模仿中理解,理解后运用、运用中反思,这么一系列思维活动所产生的结果。学生的悟需要有对象、有素材,这就是老师的讲;学生的悟需要有载体、有行动,这就是练习中的模仿、尝试、思考;学生的悟需要有过程、有空间,这就是练习中的理解、运用、反思。教师讲的太少,学生悟的素材就单薄,悟的结果就难免片面、肤浅;教师讲的太多,学生悟的空间就被挤压,难免导致思维固化、流于模仿。
解题反思是悟的核心过程,是学生对知识方法吸收内化的一个环节,是学习活动的一个高级阶段。什么时候反思?反思什么?怎么反思?我想可以从以下几个方面指导学生进行解题反思。
①对解题结果的反思。解题结果是否回答了题目的设问?解题结果是否和实际问题相吻合?推导的过程中是否改变了变量的范围?逻辑上有没有漏洞?讨论的范围是否完备?有没有遗漏什么条件、限制?等等。对解题结果的反思能使学生的思维更加严谨,同时也是解决“会而不对、对而不全”这个老大难问题的有效办法。
②对解题过程的反思。题目涉及到的知识点有哪些?它们是怎么联系起来的?解答的切入点在哪?关键点在哪?警戒点(易错的地方)在哪?还能用什么方法解(一题多解)?有哪些题也是这样做的(多题一解);条件可以变变吗?设问可以改改吗?我们不必要求学生对每一道题都做如此这般的大动作,但也绝不能每一道题都做完就丢。
“一题多解”对于促进学生沟通知识点之间的联系,对于培养学生思维的开阔、灵敏、深刻、创新,即提升学生的思维品质,对于激发学生的学习兴趣,对于充分发挥一道题的教学功能等方面确有其价值。解题教学中虽不必刻意追求“一题多解”,但也不能以“问题解决”为唯一目标,而应该让自然生动的各种解法竞相呈现。在上例中,Q8之后,可以继续:
Q9:上述解答中,求M,N两点坐标的过程运算量较大,特别是求M点的坐标。能否回避M点的坐标?——由Q5知道,用符号运算和图形运算都有可能。
Q10:如果选择符号运算,注意到AM和AN方向相反,只需要求出它们的模即可求得数量积。求|AN|仍需要N点的坐标,但求|AM|可以由“垂径定理”结合“勾股定理”实现——因为M是PQ的中点,所以|CM|即为C到直线l的距离,|CM|=|k-3|k2+1,
有|AC|=10,所以|AM|=10-(k-3)2k2+1=|3k+1|k2+1;而|AN|=5k2+1|1+3k|,
所以AM·AN=|AM|·|AN|·cosπ=-5。
Q11:如果选择图形运算,那么需要考虑向量AM能否“拆分”成坐标比较容易求的若干个向量的和(差)呢?——注意到CM⊥AM,不难想到将AM“拆分”成AC+CM(垂直关系是在研究向量数量积时,进行拆分的一个“节点”)。
其实例还有一条“幽僻”的路,甚至可以回避N点的坐标:连结CA并延长交直线m于B(见下图),则有|AB|=510,直线CA的方程:3x-y-3=0,可见CA⊥m,所以三角形AMC和三角形ABN相似,得:|AM|∶|AB|=|AC|∶|AN|,|AM|·|AN|=|AB|·|AC|=5,
所以,AM·AN=|AM|·|AN|·cosπ=-5。这个方法看似简洁明快、无限风光,但是,它来的实在太突兀、太玄妙(怎么想到连结CA、怎么想到CA⊥m、怎么想到……),没有模仿的可能、没有举一反三的可能、没有任何启发意义,这一类奇思妙想的解法,我一直认为仅供欣赏,所谓平平淡淡才是真。此外,这个方法的关键知识点是相似三角形,已经完全背离了解析几何的本质,失去了作为一道解析几何题的价值。“多解”还是“一解”,不是选题和讲题的关键,选题要看题目是能否体现概念的本质,体现重要的思想方法;讲题要让思维充分暴露、学生全程参与、过程自然流畅、解法水到渠成。
③对解题规律的反思。某一章节的问题、某一类型的问题,其求解方法往往有其规律性。
解题反思需要空间,课堂要舍得“留白”为课堂反思提供空间,课后不布置过多的作业为课后反思提供空间。
“老师领进门,修行在个人”。“领”与“修”密不可分,“领”的得法,方能“修”成正果。教学的法与度,涵盖了教学艺术的全部,非本文所能尽述;即便是数学解题的教学,也涉及知识的广度、题目的难度、课堂的密度、设计的坡度等,很难穷尽;只希望能引领学生活跃在他们现有能力的最近发展区,实现他们潜力的最大发挥。学生的悟性并非与生俱来,需要在教学中让他们有鲜明生动的感受,引导他们去触及数学中某些本质的东西,以臻通透之悟,发挥无限创造。
