带电粒子在磁场中运动题型的解题体会
2016-12-12占仟豪
占仟豪
摘 要: 带电粒子在磁场中运动规律的题目在高考题型中难度属中等偏上,但只要掌握了一定的规律方法,倘若遇到这一类型题目就能轻易解决。
关键词: 带电粒子 磁场运动 解题反思
一、对运动轨迹的研究是解题的关键
这类题型的解题步骤大体分为四步:“一点、二向、三半径、四圆心”。
1.具体来讲,首先找到运动轨迹起始的点,这一步一般来讲较为简单,这里不做赘述。
2.这里的“向”包括粒子运动方向和受力方向两方面。运动方向较为简单,包括固定方向和根据需要变化两种。粒子受力的方向一般是通过右手定则判断的,具体方法为:伸出左手,让磁感线从掌心穿过,四指指向粒子运动方向,大拇指方向即为正电荷受力的方向(即负电荷受力反方向)。做到这一步时可以适当放慢速度,否则一旦稍不留神搞错了方向,小则失去原本到手的分数,大则陷入题目越解越难的尴尬境地,影响全局。
3.判断半径的方法根据题目的不同是多样的。传统的求法是根据带电粒子在磁场中运动的半径公式:r=m*v/(q*B),这里如果式中的未知量都已被告知或已求得,不需要过多犹豫。但也有许多灵活多变的半径解法,如根据轨迹上部分点求得轨迹从而得到半径、根据题目要求达到的目的调整半径大小而求得的临界值等,大都只要求应试者较高的几何直觉和分析能力。
4.最后一步较为简单,只需根据已求得的轨迹上某点、半径、粒子运动和受力方向得到圆心。
得到粒子运动轨迹后,再通过带电粒子在磁场中运动规律的最常用两个公式,T=2*pi*m/(q*B)和r=m*v/(q*B),剩下的问题大都可以迎刃而解。
二、解题过程中要注意的问题
1.由于带电粒子受力的方向或速度大小不定,通常会造成问题的多解。这里用一个常见的例题说明:
在一匀强磁场B中,有与磁场平行的相距d两平行平板,长L,一质量为m,带电量为+q的带电粒子平行于板沿下板垂直于磁场射入,问以多大的速度,粒子才不会撞到板上?(如图)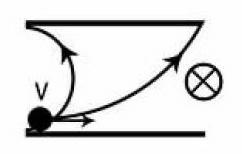
像这类题目,只需要考虑粒子运动的各种可能,并画出轨迹即可,切忌因题目过于简单而忽略一种情况。
2.对于多磁场组合或轨迹不确定的较为复杂的磁场题目,最佳办法就是将每一步的粒子运动轨迹都画出来(有时只需要考虑临界情况),一步步检查粒子的运动是否会被改变或被阻断,进而解决题目。这里给出一个例子:
质量为m,电荷量q的带正电粒子,以与边界成任意角度的相同速率射入磁感应强度为B,宽度为L的匀强磁场区域。为使所有粒子都不能穿越该磁场,求粒子的最大速度。(如右图)
解析:显然,本题的关键是找出临界条件,即发现速率相同的条件下,最容易穿越磁场的是沿磁场下边界向左射入的粒子。如果它对应的半径r=L/2(对应的轨迹圆弧如图中实线所示),将恰好到达磁场上边界,那么沿其他方向射入磁场的粒子必然不能穿越该磁场。
三、经常用到的知识技巧
1.注意粒子运动的对称性。这一点明显体现在圆形磁场中,典型的像“沿半径射入沿半径射出”。由于此类题目的这个特点较为明显,这里不做赘述。
2.注意运用三角形、圆形等几何知识做题。因为粒子圆轨道的特殊性,轨道多与直角三角形有关,而且圆本身有很多特殊性质,有时通过几何知识极易求得需要的量。这里给出一个例子:
质量m,电荷量q的带正电粒子,以速度v沿与磁场的水平直径MN平行的方向射入磁感应强度为B,半径为r的圆形匀强磁场区域,已知m*v/(q*B)>r,为使粒子在磁场中经历时间最长,入射点P到MN的距离应是多少?(如右图)
解析:设粒子在磁场中轨迹长为l,粒子运动经历的时间t=θ,与m/(B*q)成正比,又有θ=l/R与l成正比,由于轨道半径R大于磁场半径r,粒子在磁场中的轨迹是劣弧,在同圆中,劣弧越长对应的公共弦也越长。因此射入、射出点的连线应是磁场圆的直径。做出辅助线如图,tanα=tanθ/2=r/R,P到MN的距离h=r*sinα可求。
3.注意磁场的重复性和粒子运动的周期性。乍看上去很复杂的题目往往与周期有关,如果所给磁场具有较高的重复性或区域相似性,可考虑周期运动,通过研究一个或几个周期的运动从而得到整个运动过程。
一个典型的例子就是电磁场复合的回旋加速器,这里只做提示,不做过多说明。
以上这些是我在高中物理学习中总结的一些规律,具有局限性和片面性,这里仅做参考,若有不足或错误,望补充改正。
