巧用构造法证明不等式*

●谢益飞　(柯桥中学　浙江绍兴　312030)



巧用构造法证明不等式*

●谢益飞(柯桥中学浙江绍兴312030)

摘要:不等式在中学数学中处于重要地位，但不等式的证明却是一个难点．巧妙运用构造法证明不等式往往能够化繁为简、化难为易．本文介绍了运用构造法证明不等式的几种常用方法．

关键词:基本不等式;方程;函数;数列;几何图形;向量

在数学解题中，不能直接运用逻辑推理一步一步地导出必要条件而得出问题的结论时，可以跳出原来问题所设置的圈子，从新的角度用新的观点观察、分析、解释对象，别开生面地依据题设条件的特点，用已知条件中的元素为“元件”，用已知数学关系式为“支架”，在思维中构造出一种新的数学形式，或者直接构造出有关结论，使原问题中隐晦不清的关系和性质在新构造中清楚地展现出来，从而简捷地解决问题，这种解题思想称为构造．构造法有积极的和可借鉴的地方，历史上很多著名数学家，如欧几里得、欧拉、高斯、拉格朗日等人，都曾经用“构造法”成功地解决过数学难题．

构造法属于非常规思维，用构造法解题常使数学解题由难变易．不等式的证明问题是中学数学的一个难点，本文举例说明运用构造法证明不等式的几种常用方法．

1　构造基本不等式

很多不等式可以利用题设条件构造相应的基本不等式再利用有关性质进行证明．

例1设|a|，|b|，|c|均小于1，求证:

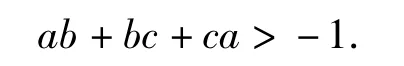
证明由条件|a|＜1，可构造不等式1+a＞0，同理可构造1+b＞0，1+c＞0，于是

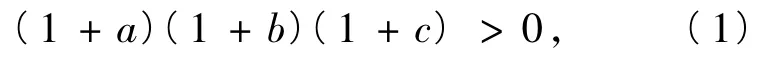
同理可得

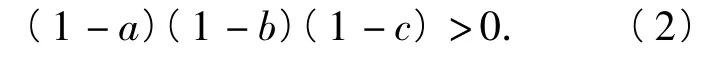
将式(1)展开得

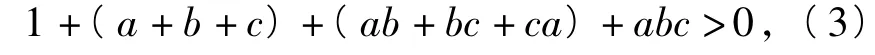
将式(2)展开得

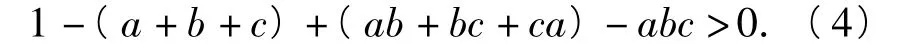
即

2　构造方程

有的不等式可以从题设或结论的外形结构作形似联想，构造出方程关系，使问题实现转化，从而获得证明．

证明由结论b2≥4ac的结构特征联想到Δ= b2－4ac≥0，从而构造一元二次方程

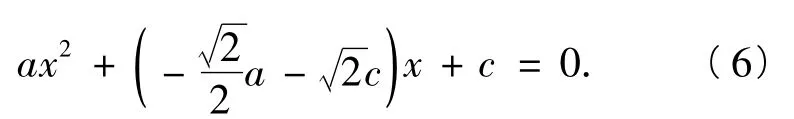
评注此题也可根据结论的特点，将题设条件2边平方得

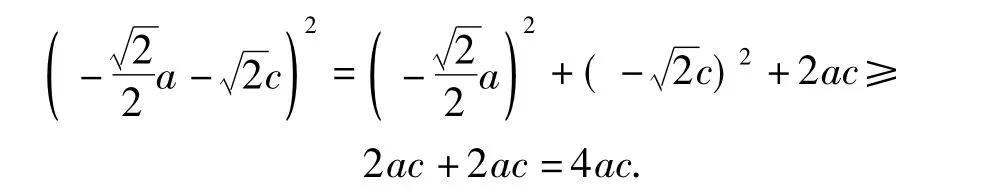
3　构造函数

有的不等式用普通方法很难证明，若巧妙构造函数，运用函数思想，则能迎刃而解．例3已知x，y，z∈(0，1)，求证:

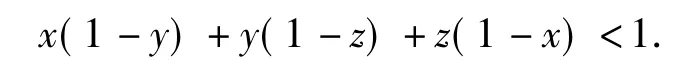
(第15届俄罗斯数学竞赛试题)

证明构造函数

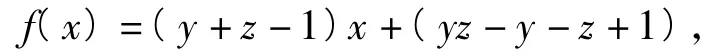
因为y，z∈(0，1)，所以

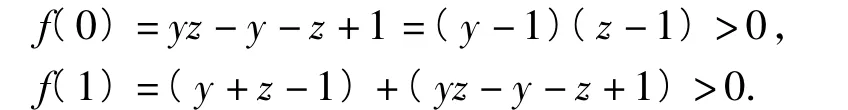
而f(x)是一次函数，其图像是直线，又x∈(0，1)，故恒有f(x)＞0，即(y+z－1)x+(yz－y－z+1)＞0，整理可得x(1－y)+y(1－z)+z(1－x)＜1．

评注此题条件、结论均具有一定的对称性，然而难以直接证明，构造函数简单快捷．

例4已知a，b为实数，并且e＜a＜b，其中e是自然对数的底，证明:ab＞ba．

证明当e＜a＜b时，要证ab＞ba，即证blna＞alnb，只需证构造函数(其中x＞e)，求导得，因为当x＞e时，lnx＞1，所以y'＜0，从而函数在(e，+∞)上是减函数，又e＜a＜b，故，即ab＞ba．

评注该题构造函数，并运用了导数的性质判断函数的单调性，从而证明不等式．

4　构造数列

相当多的数学问题，尤其是证明不等式，尝试“构造数列”能产生意想不到的效果．

例5对一切非零自然数n，求证:

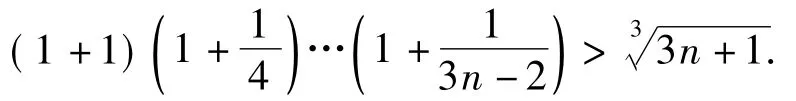
证明构造数列{an}，使其通项为

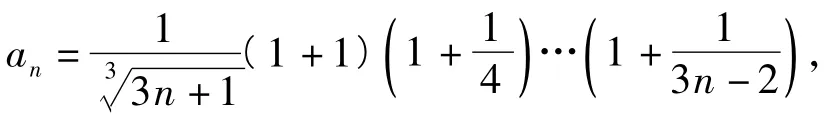
则

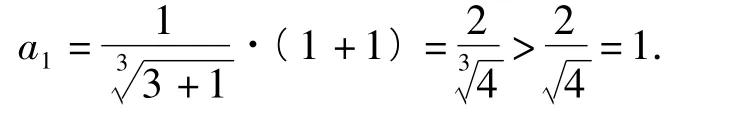
因为

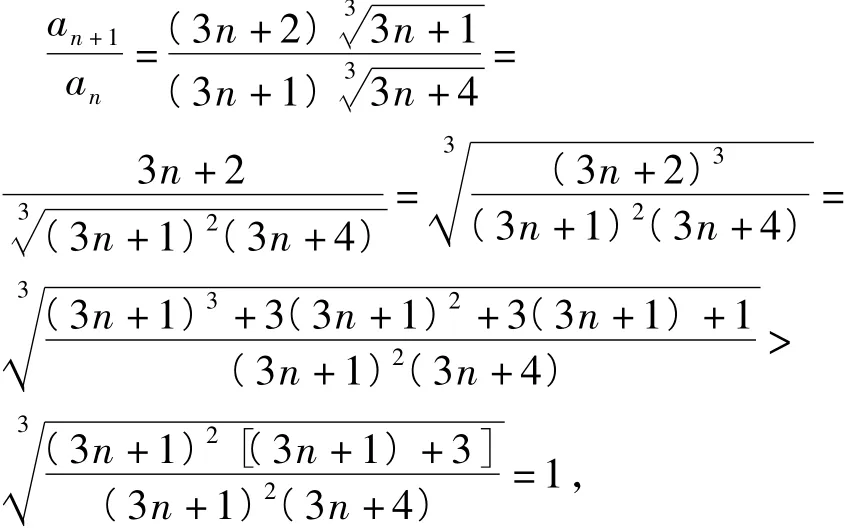
所以an+1＞an(其中n∈N*)，从而对一切自然数n，都有an≥a1＞1，即

评注与自然数有关的不等式证明，最常规的方法是数学归纳法和放缩法，但数学归纳法往往过程较繁，放缩法盲目性较大，通过构造数列的方法可使证明过程更加简洁明快．

5　构造几何图形

若要证明的不等式中的数量关系有明显的几何意义，则可以通过某种方式与几何图形建立联系，构造图形，将题设中的数量关系直接在图形中体现，然后在构造的图形中寻求结论．

例6如果x1，x2的绝对值不大于1，求证:

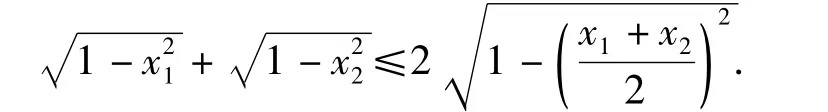
证明在直角坐标系内作单位圆，⊙O的方程为x2+y2=1．如图1，取OM1=x1，OM2=x2，作N1M1⊥x轴交⊙O于点N1，作N2M2⊥x轴交⊙O于点N2，则取M1M2的中点M，显然

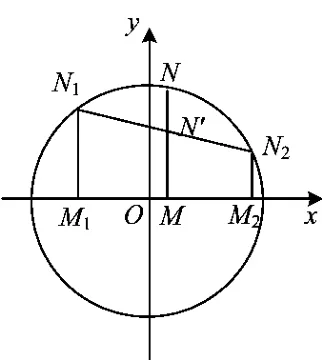
图1

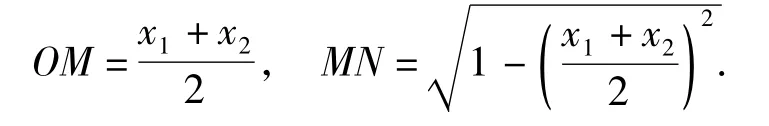
设MN交N1N2于点N'，由梯形的中位线定理知

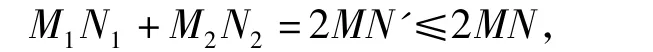
即

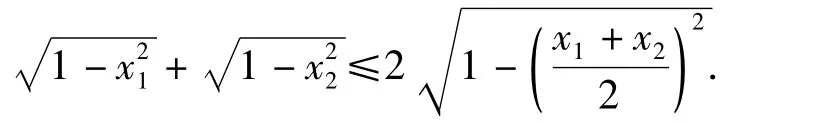
6　构造向量

代数、几何、三角函数中的很多问题都可以利用向量来解决，不等式的证明问题有时也可以引入向量来解决．

例7设a，b，c，d为非零实数，求证:

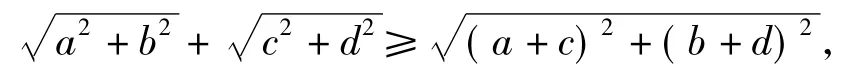
并说明等号成立的条件．

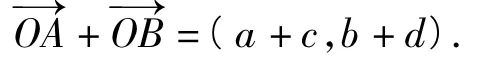
由向量的三角形法则知

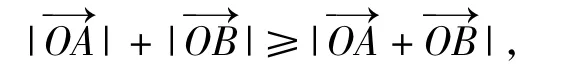
评注类似可证明

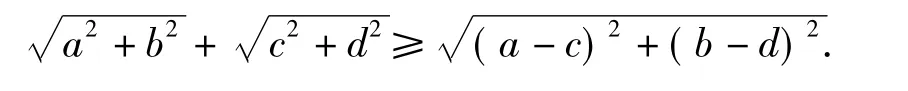
作者简介:谢益飞(1983－)，男，浙江绍兴人，中学一级教师，研究方向:数学教育．

修订日期:*收文日期:2016-01-29;2016-02-29．

中图分类号:O122．3

文献标识码:A

文章编号:1003－6407(2016)04-16-02