数形结合思想在解题中的应用

2016-03-14曾润展

考试周刊 2016年4期

曾润展

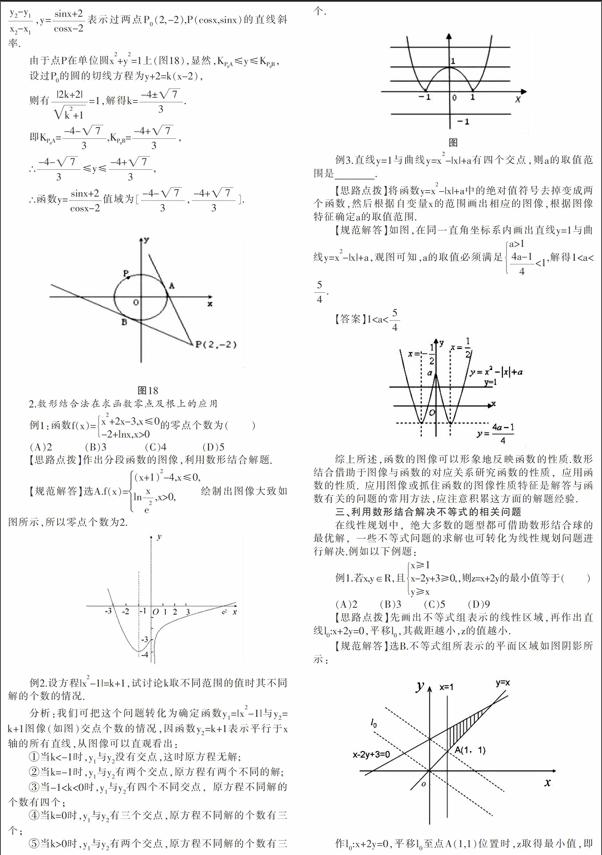
摘要：数形结合是数学解题中常用的思想方法，是解答高考数学试题一种常用方法与技巧，是根据数量与图形之间的关系，认识研究对象的数学特征寻找解决问题方法的一种数学思想.数学中两大研究对象“数”与“形”的矛盾统一，是数学发展中的内在因素，数形结合贯穿于数学发展中的一条主线，巧妙运用“数形结合”思想解题，可以化抽象为具体，效果事半功倍.

关键词：数形结合思想几何图形数量关系解决问题

数学内容丰富多彩，其解题思路灵活多变，很多题目的解法并不唯一.同一道题，因为选择的方法不同往往繁简差异很大，所以能否选择恰当的方法进行求解至关重要.数学的两大元素是数与形，它们彼此关系紧密，常常结合在一起，内容上互相联系，方法上互相渗透，在整个数学中的地位举足轻重.数形结合在数学解题中的应用的广泛性是大家有目共睹的.对于很多或者简单或者复杂的数学问题，我们可以引入图形，利用数形结合进行处理，从而使繁琐的数的问题转化为直观的图形.下面我就利用一些高考题及某些相关题目谈谈数形结合是数学解题中的应用.

一、集合中的数形结合

1.利用数轴解决集合的有关运算和集合的关系问题

如：当几个集合的解集是不等式形式，要求它们的交集或并集时，经常借助于数轴，把不等式的解集在数轴表示出来，通过数轴观察它们的交集或并集，这样比较直观.

综上所述，数形结合思想贯穿于整个数学学习中，将其利用得好能有效简化数学运算过程，轻松获得解题思路，提高解题能力.

应用数形结合思想，就是要充分考查数学问题的条件和结论之间的内在联系，既分析其代数意义又揭示其几何意义，将数量关系和空间形式巧妙结合，寻找解题思路，使问题得到解决.

那么，怎样才能更好地利用数形结合进行数学解题呢？我认为主要应做到以下几点.

1.深刻领会数学概念，熟练掌握数学基础知识.

2.认真审题，最大限度地挖掘题目中存在的各种条件.

3.必须准确作图.准确作图往往是良好思路的开端，有时候甚至直观地给我们正确的答案，而不精准的作图有时会对解题造成某种误导.

4.注意培养各种解题能力.

要在解题中很好地利用数形结合不是简单地记住数学概念与作用便能达到要求，必须在平常的解题中注意各种数学能力的培养.比如：运算能力，逻辑推理能力，空间想象能力，以及良好的记忆力.只有各种数学解题能力提高了，才能在数学解题中真正灵活地利用数形结合思想.

参考文献：