畸形波作用下半潜式平台的极限生存能力评估

李志富，任慧龙，李 辉

（哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

畸形波作用下半潜式平台的极限生存能力评估

李志富，任慧龙，李 辉

（哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

极限海浪可能对海洋平台的安全造成极大的威胁，故合理地评估平台在此海况下的运动响应和系泊缆索的动张力响应对平台设计具有重要意义。文章首先利用新波理论和随机海浪理论建立了畸形波入射波模型。然后利用间接时域方法和非线性有限元法分别建立了平台主体运动和系泊缆索动力响应的求解方程，并根据导缆孔的平衡方程建立了平台主体和系泊缆索的时域耦合运动方程。最后深入分析了某半潜平台在畸形波作用下的运动响应和系泊缆索的动张力响应，对平台的极限生存能力进行了评估。

畸形波；半潜式平台；耦合响应；非线性有限元；极限生存能力

0 引 言

海洋浮式平台所处工作环境复杂多变，海浪、大风、急流等时常发生，极大地限制了平台的正常作业。尤其是恶劣海况下不时出现的畸形波，对海洋平台的安全性造成了极大的危害。因此，研究畸形波作用下的半潜式平台的运动响应具有重大的意义。

1991年Tromas[1]从概率角度出发提出了用于模拟极限波面升高的新波理论，但是该方法由于略去了随机波高，使得所模拟的极限波面升高在最大值发生时刻附近很快便衰减为零，与实际的恶劣海况下出现畸形波的波面形状有较大的差别，因此本文利用随机海浪理论对其进行了修正，提出了“随机新波理论”。对于平台和系泊系统的耦合运动响应，有很多学者进行了研究[2-6]。对于浮式平台的全耦合计算主要有频域耦合计算和时域耦合计算，但是考虑到水动力和缆索等非线性因素的影响，较为可靠的手段是采用时域耦合方法。

本文首先介绍了基于海浪谱进行海浪模拟的新波理论和随机海浪理论，并利用随机海浪理论对新波理论模拟极限海况时的不足进行了合理修正，建立了随机新波理论。其次在时域内建立了平台与系泊缆索的耦合动力模型，该动力模型能够有效地计及系泊缆索几何非线性和材料非线性。最后基于同一海浪谱，分别根据随机海浪理论和本文所建立的修正后的新波理论建立了随机波浪入射波模型和畸形波入射波模型，并深入分析了某半潜式平台在畸形波作用下的运动响应和系泊缆索的动张力响应，对该半潜式平台在极限海况下的生存能力进行了评估。

1 畸形波数值模拟

1.1 新波理论

将畸形波波面升高看作是N个线性规则波的叠加：

将海洋波浪看成是一个平稳的、各态历经的随机过程，波面升高的条件概率分布近似服从高斯分布。波面升高的最大值ηα发生于 （x0，t0），则畸形波波面升高的联合条件概率分布可以写为：

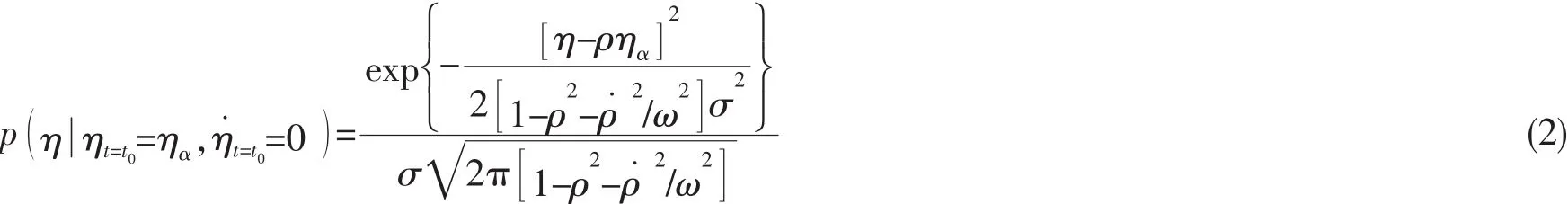
式中：

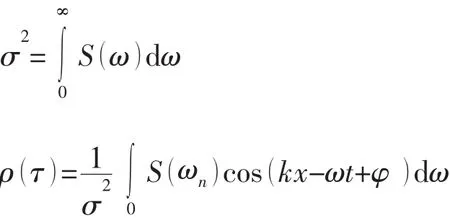
通过求解（2）式的最大值，最终可以推导出极限波面升高的表达式：

上式右端第一项为最可能波面升高，第二项为波面升高的随机部分。

1.2 随机海浪理论

大量实测资料证明，自然界中的随机海浪在很长一段时间内具有高斯正态分布的特征，是一个平稳的、各态历经的随机过程。对于随机海浪，一般用海浪谱方法进行研究。目前，工程界中常用的深水海浪谱主要有Neumann谱、P-M谱、ITTC谱以及JONSWAP谱。

本文采用JONSWAP海浪谱，其表达式：

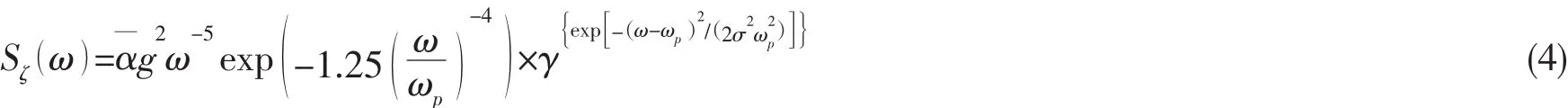
设定最大波高发生的节点 （x0，t0）=（100 m，200s）时，忽略随机波高部分，由（3）式和（4）式模拟得到的极限波面升高如图1所示。

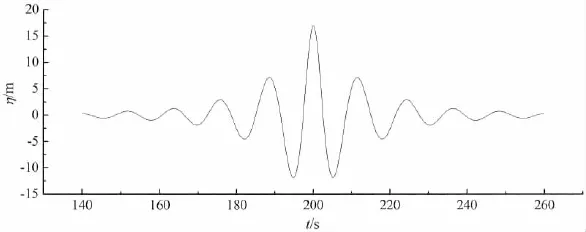
图1 新波理论模拟的畸形波Fig.1 Freak wave elevation based on the new wave theory

由图1可以看出，由于忽略了波高中的随机部分，使得最大波高很快便衰减为零，与大部分所测得畸形波波面时历不相符。由于频域计算为线性系统，因此忽略随机部分对于平台耦合响应的最大值并没有影响。但是对于平台的时历耦合响应，由于记忆效应的存在，最大波高附近的波浪形式对于最大波高处的响应会产生一定的影响，因此忽略波高的随机部分便不再合理。

1.3 随机新波理论

为解决利用新波理论所模拟的极限波面升高快速衰减的问题，本文利用随机海浪理论对最可能波高中的随机波高的部分予以了修正。

随机海浪理论模拟的波面升高：

用（5）式来表达（3）式中的随机波高部分，所模拟的极限波面升高如图2所示。

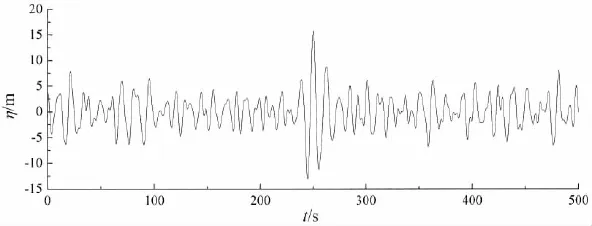
图2 随机新波理论模拟的畸形波Fig.2 Freak wave elevation based on the random new wave theory

由图2可知，利用本文修正后的新波理论所模拟的恶劣海况下出现畸形波的波面升高历程，在距离最大波面升高位置一定距离以后逐渐趋于稳定的随机波动形式，与图1相比更符合实际测得畸形波出现的海况。

2 平台耦合运动方程

2.1 平台主体运动方程

对于绕射问题的时域求解，本文主要通过间接方法进行计算，即首先求解频域波浪干扰力的频率响应函数，然后利用卡明脉冲响应的做法求得时域波浪激励力Fwave（t）：

式中：hF（t）为波浪激励力脉冲响应函数，HF（iω ）为波浪激励力频率响应函数。

对于辐射问题的时域求解，通过延迟函数将频域内的波浪辐射力转化为带卷积积分形式的时域波浪辐射力，形式如下：

式中：K（t）为时域延迟函数，μ（∞）为频率趋于无穷时的附加质量。

在计算时域波浪辐射力时，由延迟函数计算公式（10）可知，为了求得时域延迟函数，必须计算整个频率范围内的阻尼系数，为避免过大的数值误差，本文采用了半数值半解析的方法进行了计算[7]。

由时域波浪激励力和辐射力可以建立平台主体的时域运动方程：

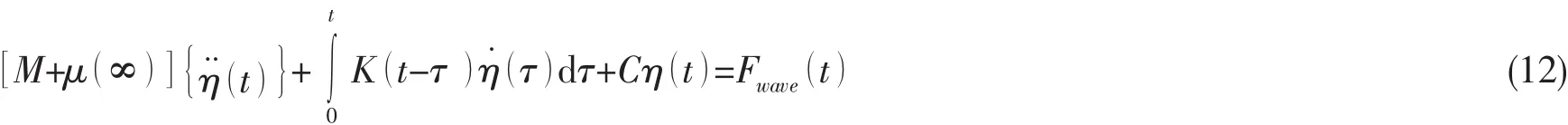
2.2 系泊缆索运动方程

对于系泊缆索动力响应的计算，本文主要采用了非线性有限元方法[8]。缆索微段在重力、浮力、流力、张力和惯性力的作用下保持平衡，其动力控制方程如下式：

式中：W为缆索净重力，T为缆索张力，I为缆索惯性力，F为流体对缆索微段的作用力。

对于整个系泊缆索，其着链点处的运动应与浮体在该处的运动相同，链锁底端的位置应为常值，即：

将系泊缆索离散为两节点的杆单元，并利用系泊缆索的动力控制方程和边界条件，最终可以得出用于T.L.格式的矩阵求解方程，即：

2.3 平台耦合运动方程

建立时域耦合运动方程的关键在于构造导缆孔处的平衡方程，其形式如下：

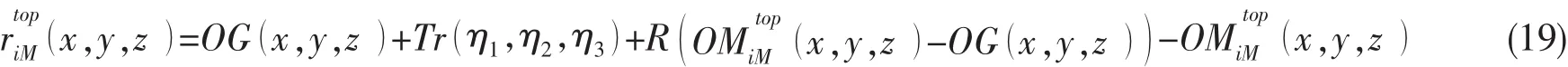
系泊缆索作用于浮式平台主体的总力可以写为：

系泊缆索作用于浮式平台主体的总力矩可以写为：

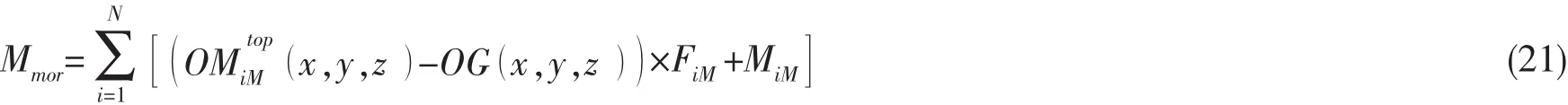
则浮式平台系统的时域耦合运动方程可以写为：

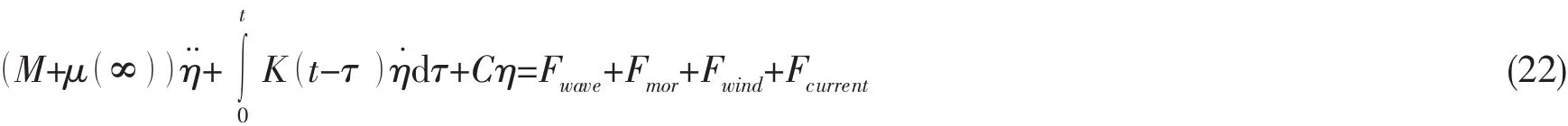
式中：Fwave为波浪激励力，Fmor为锚泊系统顶端节点张力。

3 畸形波作用下半潜平台动力响应

3.1 入射波波面升高

海浪谱采用JONSWAP谱，海浪谱相关参数如表1所示，分别根据随机海浪理论和本文所建立的修正后的新波理论建立了随机波浪入射波模型和畸形波入射波模型，波面升高如图3所示。

表1 入射波模拟参数Tab.1 Simulation parameters of the incident waves

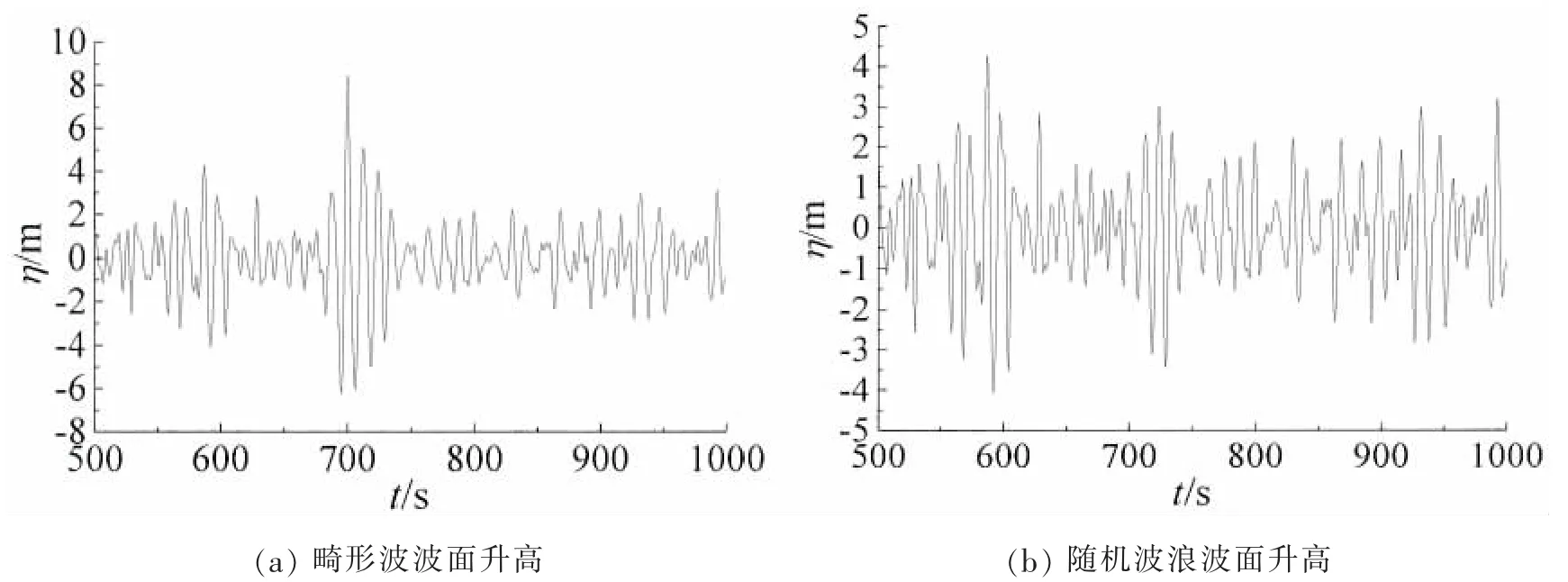
图3 入射波波面升高Fig.3 The incident wave elevations

由图3可知，在基于同一能量谱的前提下，利用本文所建立的畸形波入射波模型所得出的最大波面升高（8.52 m）比根据随机海浪理论建立的入射波模型所得出的最大波面升高（4.26 m）要大得多。因此利用本文所建立的修正后的新波理论建立的入射波模型来评估平台的极限生存能力较随机海浪理论更为合理。

3.2 平台及系泊缆索耦合动力响应

根据基于修正后的新波理论所建立的畸形波入射波模型（图3），计算了某半潜式平台在该入射波作用下的运动响应和系泊缆索的动张力响应。平台主体水动力模型如图4所示，平台和系泊缆索的结构参数及系泊缆索的布置形式如表2、表3和表4所示。

由于该半潜式平台具有两个对称面，且四根系泊缆索对称布置，因此本文选取了0°、45°、90°三个典型的浪向进行了计算。因为海洋平台的极限生存能力取决于整个模拟时间段内的平台摇荡运动的最大值和系泊缆索张力响应的幅值，故本文分别给出了各浪向角下平台的垂荡、横摇、纵摇和各锚链的动张力响应。

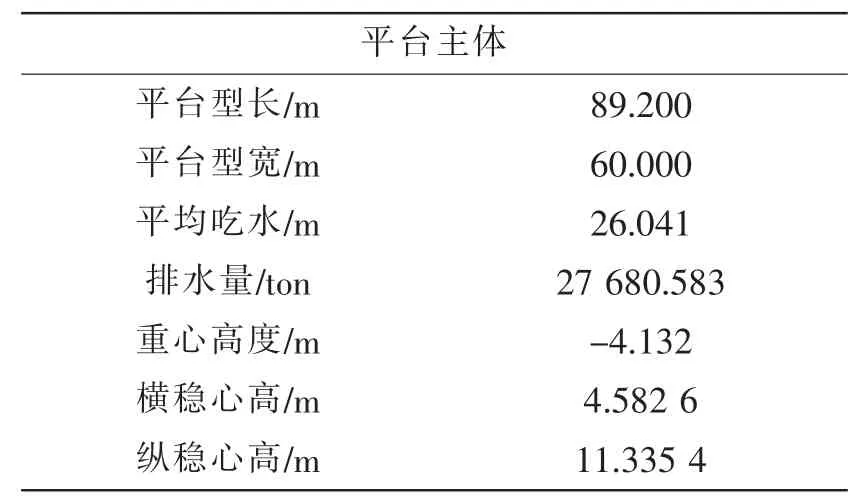
表2 平台主体结构参数Tab.2 Properties of the semi-submersible platform

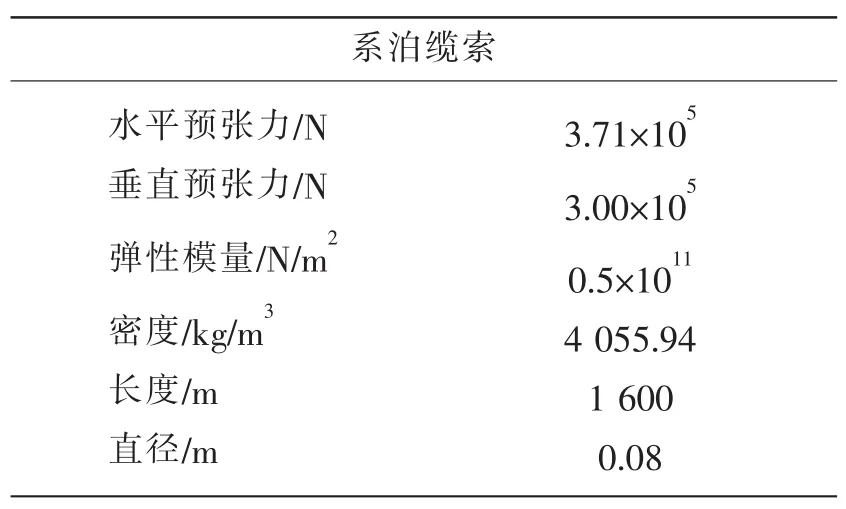
表3 系泊缆索相关参数Tab.3 Properties of the mooring cable

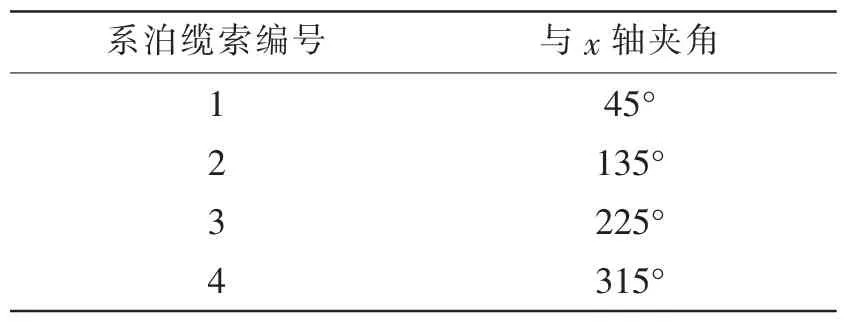
表4 系泊缆索与x轴夹角Tab.4 The angles between mooring lines and x axis

图4 平台主体水动力计算模型Fig.4 Panel distribution on the semi-submersible platform

由于所模拟的极限海况的最大波高出现在700 s，因此本文给出了垂荡、横摇、纵摇和各锚链的动张力响应在690～740 s之间的时历曲线（图5～11）。由图5可知，当浪向角为0°时，平台的垂荡运动响应最大，为4.22 m。由图6可知，当浪向角为90°时，平台的横摇运动响应最大，为0.08 rad。由图7可知，当浪向角为0°时，平台的纵摇运动响应最大，为4.22 m。由图8可知，当浪向角为90°时，1#系泊线的动张力响应出现最大值，为8.89×105N。由图9可知，当浪向角为45°时，2#系泊线的动张力响应出现最大值，为12.13×105N。由图10可知，当浪向角为0°时，3#系泊线的动张力响应出现最大值，为11.13×105N。由图11可知，当浪向角为90°时，4#系泊线的动张力响应出现最大值，为8.01×105N。且各响应的最大值出现的时刻均晚于最大波高出现的时刻（700 s）。

锚泊线的断裂将直接导致平台的倾覆，因此锚泊线的最大张力是平台极限生存能力的重要指标，对于本文中的计算模型，锚泊线的最大张力发生于2#系泊线，为12.13×105N，产生于入射波浪向为45°时的海况。

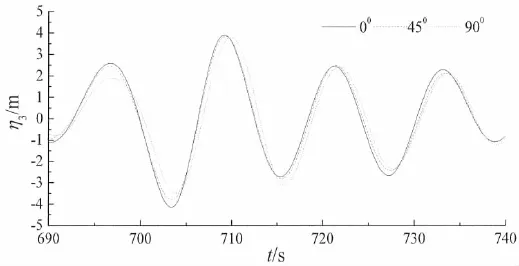
图5 平台垂荡运动响应Fig.5 Heave response of the platform

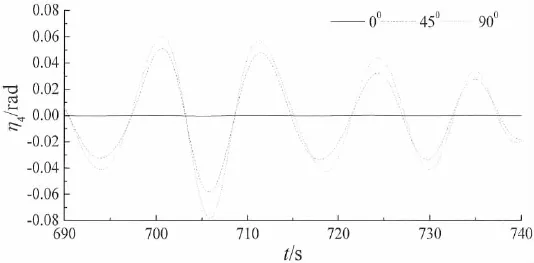
图6 平台横摇运动响应Fig.6 Roll response of the platform

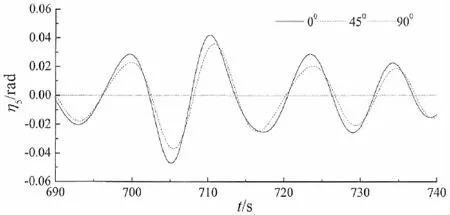
图7 平台纵摇运动响应Fig.7 Pitch response of the platform

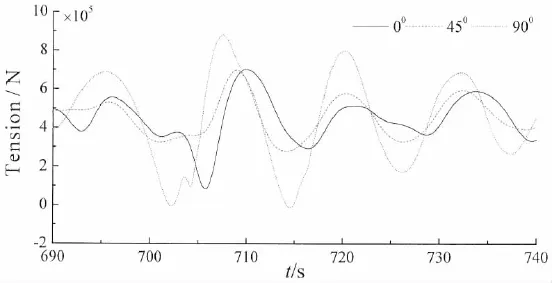
图8 1#系泊缆索动张力响应Fig.8 Tension response of the 1#mooring cable

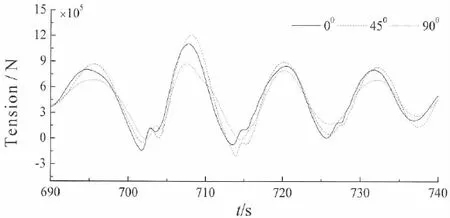
图9 2#系泊缆索动张力响应Fig.9 Tension response of the 2#mooring cable

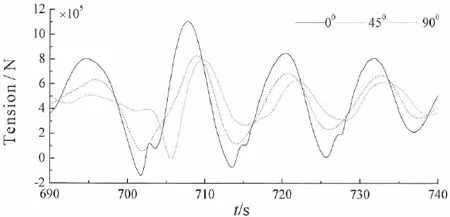
图10 3#系泊缆索动张力响应Fig.10 Tension response of the 3#mooring cable

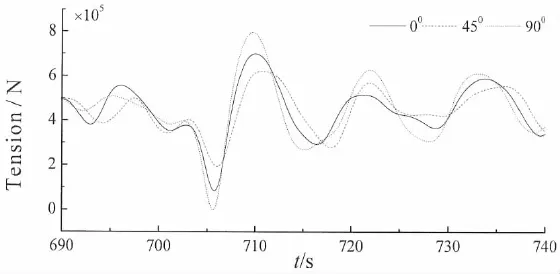
图11 4#系泊缆索动张力响应Fig.11 Tension response of the 4#mooring cable

4 结 论

利用本文所提出的修正随机新波理论能够较好地模拟畸形波的波面升高，解决了新波理论在模拟畸形波波面升高快速衰减的问题；采用间接时域方法和非线性有限元方法建立的浮体和系泊缆索的耦合运动模型可以有效地进行耦合动力响应分析；浮体运动响应对入射波方向的变化不敏感，但是系泊缆索的动张力响应对入射波方向的变化较为敏感；运动响应和动张力响应的最大值出现的时刻均晚于最大波高出现的时刻；对于本文的计算模型，2#系泊线的张力响应最大值最大，为12.13×105N，发生在浪向角为45°时的海况。

[1]Tromas P S,Anaturk A,Hagemeijer P.A new model for the kinematics of large ocean waves application as a design wave [C]//Proc.1st Int.Offshore and Polar Engineering Conference(ISOPE).Edinburgh：[s.n],1991.

[2]李彬彬,欧进萍.深吃水多立柱平台的运动响应分析[J].中国造船,2010,51(2)：107-116. Li Binbin,Ou Jinping.Motion analysis of a deep draft multi-spar platform[J].Shipbuilding of China,2010,51(2)：107-116.(in Chinese)

[3]肖 越,王言英.浮体锚泊系统计算分析[J].大连理工大学学报,2005,45(5)：682-686. Xiao Yue,Wang Yanying.Computational analysis of moored floating-body[J].Journal of Dalian University of Technology, 2005,45(5)：682-686.(in Chinese)

[4]孙金伟,王树青.系泊模式对Spar平台运动性能的影响[J].中国海洋大学学报,2010,49：147-153. Sun Jinwei,Wang Shuqing.Study on motion performance of deepwater spar platform under different mooring methods[J]. Periodical of Ocean University of China,2010,49：147-153.(in Chinese)

[5]王兴刚,孙昭晨,梁书秀.深水Spar平台在不规则波中的运动响应[J].中国造船,2011(2)：16-24. Wang Xinggang,Sun Zhaochen,Liang Shuxiu.Motion responses analysis of moored spar platform in irregular waves in deepwater[J].Shipbuilding of China,2011(2)：16-24.(in Chinese)

[6]周素莲,聂 武,白 勇.深水半潜式平台系泊系统设计研究[J].船舶力学,2010,14(5)：495-502. Zhou Sulian,Nie Wu,Bai Yong.Investigation on mooring system design of a deepwater semi-submersible platform[J]. Journal of Ship Mechanics,2010,14(5)：495-502.(in Chinese)

[7]Cao Yusong.A procedure for evaluation,assessement and improvement of added mass and radiation damping of floating structures[C].OMAE,2008-57275.

[8]Yang Mindong,Teng Bin.Static and dynamic analysis of mooring lines by nonlinear finite element method[J].China O-cean Engineering,2010,24(3)：417-430.

Safety of semi-submersible platform under extreme waves

LI Zhi-fu,REN Hui-long,LI Hui
(Department of Ship Building,Harbin Engineering University,Harbin 150001,China)

The extreme waves may be a great threat to the offshore platforms,so the accurate prediction of the motion and tension response under extreme waves is of great importance.In this paper,the incident freak wave model was constructed by the random wave theory and new wave theory.The dynamic equations of the floating offshore structures and mooring cables were established by the indirect time-domain method and non-linear finite element method,respectively.And,the coupled motion equation was built based on the‘equilibrium equations of fairlead points’.Finally,the coupled response of semi-submersible platform under freak waves was analyzed,and the extreme safety of the platform was evaluated.

freak waves;semi-submersible platforms;coupled response; non-linear finite element method;extreme safety

U661.4

：Adoi：10.3969/j.issn.1007-7294.2016.05.010

1007-7294（2016）05-0591-09

2015-12-16

国家973基金资助项目（2011CB013703）；国家自然科学基金资助项目(51279034)

李志富（1990-），男，博士研究生，E-mail：lizhifu@hrbeu.edu.cn；任慧龙（1965-），男，教授，博士生导师，E-mail：renhuilong@263.net。