基于恒定陡度聚焦波模型的分析与讨论
2020-02-22郭骞隶谷汉斌
郭骞隶,谷汉斌
(1.浙江海洋大学,舟山 316000;2.宁波大学 土木与环境工程学院,宁波 315211)
聚焦波一般也叫极端波、疯狗浪、怪波等。它是指海洋上突然出现的一种波高很大的情况,一个波列过程中,最大波波高是次大波波高的两倍以上。它对海洋结构物、海洋工程、海上船舶等具有巨大的危害。因此,聚焦波的模拟及其特性研究在海洋水动力学、海洋工程应用等方面具有重要价值和意义[1]。物理上,有四种方式产生聚焦波[2],即波流相互作用、波与海底相互作用、波波相互作用和风波相互作用。本文只考虑波波相互作用。对于波波相互作用产生聚焦波,理论上有两种方式[2],一种是利用不规则波的生成方式,它需要不同波浪频率成分很长的叠加时间,才可能出现这种聚焦波,主要特点是出现时间或地点不确定;另一种是相位速度调整的方式,本文就介绍这种方式,它的各个组成波同时在特定时间点和特定位置到达峰值。波波相互作用的聚焦波研究的基础是Longuet-Higgins[3]的不规则波模型;它采用线性叠加原理,通过调整相位使各组成波在某一个时间和某一地点聚集起来,形成聚焦波。近年来,聚焦波问题是一个研究热点。Schaffer研究了实验室如何产生聚焦波。Fochesato[4],Yan 和 Ma[5],Turnbull[6],NIGN D Z[7],Bai和Eatock Taylor[8]等,通过数值波浪水池模拟生成聚焦波以及聚焦波与结构的相互作用。聚焦波模型是物理和数值模拟产生聚焦波的基础,Kway J H L等[9]在1998年提出了应用恒定振幅谱的方式产生聚焦波。
在波聚焦的过程中,波的振幅实际上是任意的,它们既可以恒定为常数,也可以假设它们与对应的波数成反比[2]。本文中使用的恒定陡度方式与恒定振幅谱[9]相比能够得到一个良好的破碎聚焦波,而一般在实际工程中聚焦波通常都是破碎的。并且恒定陡度方式与采用频谱理论模拟聚焦波不同,它不需要知道谱型、有效波高、特征周期等参数;只需要恒定陡度和频率范围,按色散关系由水深确定波数,再确定波幅,就可以获得聚焦波的表达式。本文通过改变水深、组成波频率范围、中值频率和恒定陡度,得到对应的恒定陡度形成的聚焦波,分析了聚焦波的特征和规律。这些特征和规律有助于采用该方式快速获得需要的聚焦波。
1 基于恒定陡度形成聚焦波
Longuet-Higgins给出了不规则波的波面过程表达式
(1)
式中:an和ωn分别为各个组成波的振幅和角频率;εn是随机数,取值在(0,2π)范围内,在此基础上人们把波浪看成定常随机过程,可以看作不同组成成分的余弦波叠加而成。任意时间和位置的波面过程表示为[10]
(2)
式中:N为组成波的个数;ai为组成波的波幅;ωi为组成波的角频率;ki为组成波的波数;φi为组成波的初始相位。组成波的频率和波数满足色散关系
(3)
假定波浪在指定时刻t=tf时聚焦于指定位置x=xf,各组成波在该处叠加,则要求各组成波的初相位应满足
φi=-kixf+ωitf+2mπ,m=0,±1,±2,…
(4)
将φi代入到式(2)中,令m=0,这时任意位置处的波面过程η(x,t)为
(5)
在式(5)中ai和ki是未知量,这是需要来解决的关键。Sriram等[2,9,11]假定单个组成波的波幅ai与波数ki的乘积为常数,并定义此常数为恒定陡度Si,采用振幅增益常数Ga来表示单个余弦波的恒定陡度Si,Ga表示为
Ga=Si/π=aiki/π=c
(6)
c表示常数;意味着各组成波具有相同的振幅增益。因此,一旦频率范围确定,采用等区间分割,很容易给出各组成波的频率,相对应的波幅ai与波数ki就可以求得。而聚焦波的恒定陡度S是所有组成波的恒定陡度Si的求和,即
(7)
当设定好Ga后,就可以方便地求出与之对应的圆频率ωi、波数ki与振幅ai,由式(5)表示出聚焦波随空间和时间的变化。
按照上述方式,确定聚焦波频率范围(最高频和最低频)、恒定陡度S(也可以用Ga代替)和水深,计算出聚焦波波面过程;然后研究水深、组成波频率范围、中值频率和恒定陡度对聚焦波波形的影响。
2 聚焦波波形
为了便于分析研究,依据频率的高低分成了低频和高频两种情况,进行了不同参数变化情况下大量的计算。低频适用于实际海洋环境、高频适用于实验室试验。但这里没有考虑波浪破碎的问题,实际上当波面陡度达到一定程度,波面从波峰处开始破碎;这个问题留待以后研究,本文不予讨论。
2.1 低频情况
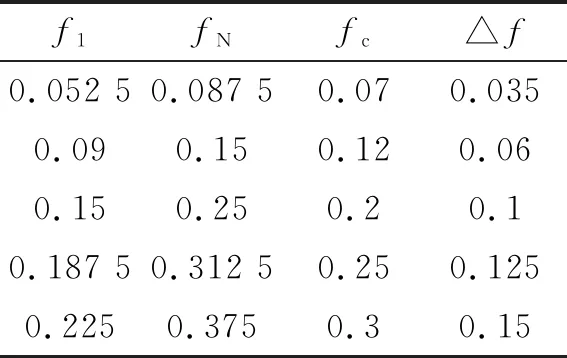
表1 不同fc的低频聚焦波参数
实际海洋环境中,波浪周期在几秒到十几秒之间。本文参照东海海域波浪周期范围3~15 s[12]作为聚焦波实际波浪周期取值范围,把周期换算成频率,按色散关系2πL=T2gtan(2πd/L),求得组成波波长,再计算组成波波数;选取其中5个频率中值fc(fN=fc+△f/2),分别为0.07 Hz、0.12 Hz、0.2 Hz、0.25 Hz、0.3 Hz;并以此计算聚焦波波形。计算时聚焦时间取100 s、聚焦位置取0 m,组成波个数N取为32。为了研究水深影响,考虑5个水深分别为8 m、15 m、20 m、30 m、45 m。设f1为频率范围的起始频率,fN为频率范围的终止频率,△f=fN-f1为聚焦波的频率组成范围。在△f/fc=0.5和Ga=0.002不变的情况下,分别进行5个水深的计算。参数取值见表1。
图1是水深8 m时恒定陡度谱模型理论计算的波面时间过程,其他水深时波形类似,只是幅值不同;图2给出不同水深情况下,最高波面峰值的变化;当fc较小时(如0.07 Hz),最高波面峰值随水深增大显著增大;当fc较大时(如0.3 Hz),最高波面峰值随水深增大不明显;同一水深情况下,fc越小,最高波面峰值越大。所有这些组次,最高波面峰与次高波面峰值的比值接近于1.58。

图1 不同fc的低频聚焦波波面过程线
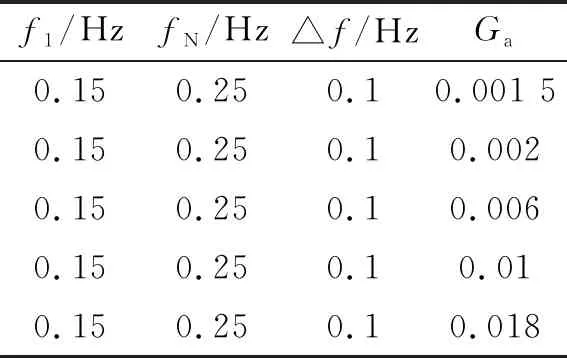
表2 不同Ga的低频聚焦波参数
Sriram设置参数Ga范围为0.001 5~0.006[2],本文为探讨Ga对波形影响规律,选择覆盖Sriram设置的范围,便于应用。具体范围0.001 5~0.018,并在水深8 m、15 m、20 m、30 m、45 m的情况下,进行了聚焦波波形计算,此时聚焦时间100 s、聚焦位置为0 m,组成波个数N为32。计算中△f/fc=0.5,其他参数见表2。
图3为计算的聚焦波波面时间过程线,同一水深情况下,Ga越大,最大波面峰值越大。图4给出最大波面峰值与水深的关系,同一水深情况下,Ga越大,最大波面峰值越大;同一Ga情况下,水深越大,最大波面峰值越大;当Ga值较小(0.002)时,最大波面峰值随水深增加不显著;而当Ga值较大(0.018)时,最大波面峰值随水深增加显著增大。最大波面峰值与次高峰值之比接近常数1.58。

图3 不同Ga的低频聚焦波波面过程线
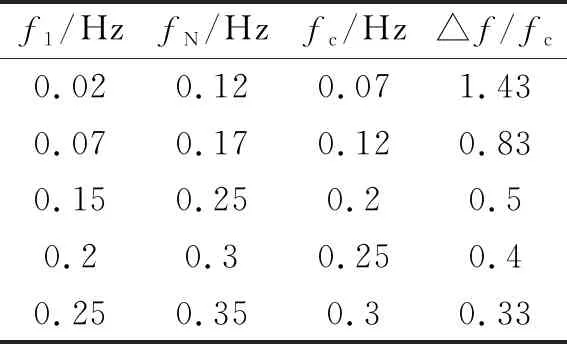
表3 不同△f/fc的低频聚焦波参数
当fc分别为0.07 Hz、0.12 Hz、0.2 Hz、0.25 Hz、0.3 Hz,△f取0.1,Ga取0.002,其他参数见表3。计算聚焦时间100 s、聚焦位置0 m,组成波个数N为32,水深分别为8 m、15 m、20 m、30 m、45 m。
图5为水深8 m时聚焦波波面过程线。参数fc越小(如0.07 Hz),最高波面峰值越高,次高波峰位置越远离最高波峰,它们之间产生的波面起伏越多;fc越大(如0.3 Hz),最高波面峰值越低,最高波面峰与次高波面峰离得越近。其他水位与8 m水深情况类似,只是最高波面峰值随水深增大而增大(图6)。
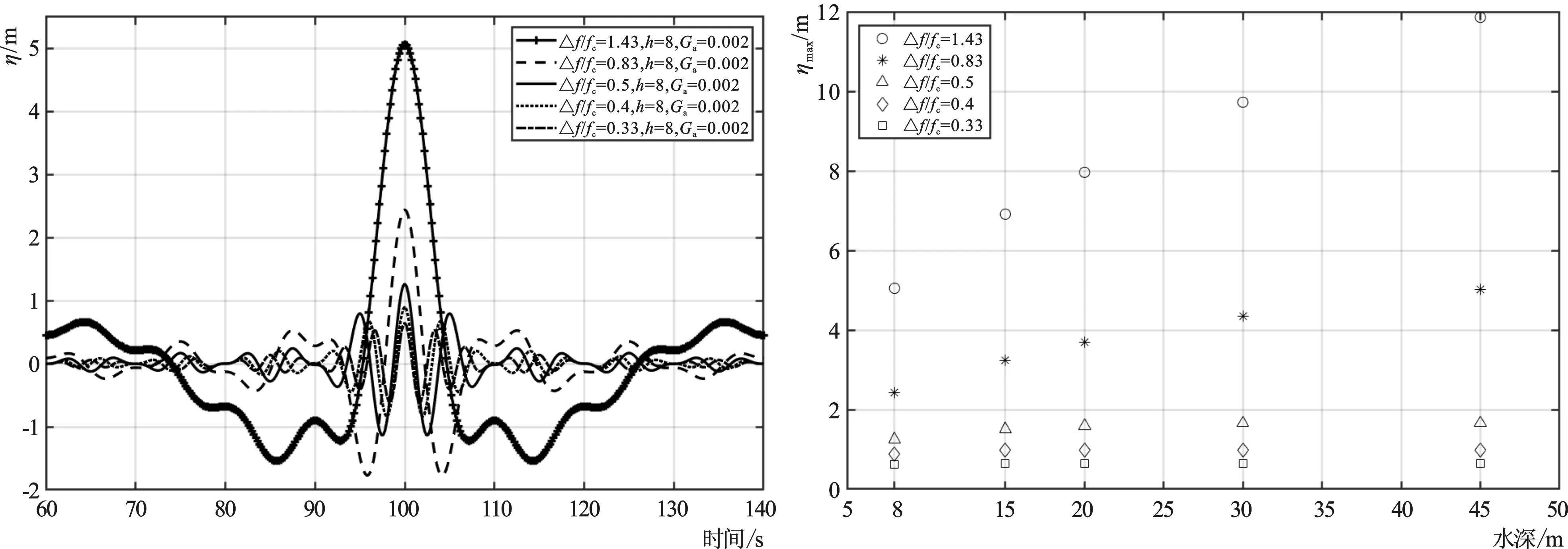
图5 不同△f/fc的低频聚焦波波面过程线

图7 最高峰与次高峰比值和Δf/fc关系图
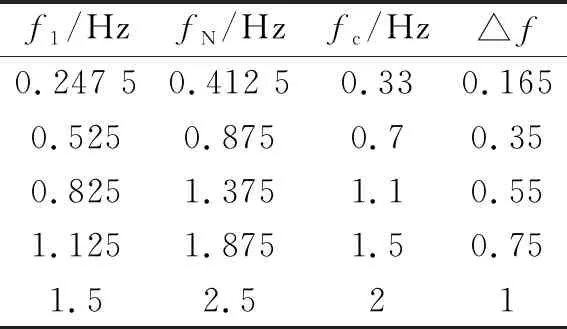
表4 不同fc的高频聚焦波参数

表5 不同Ga的高频聚焦波参数
在聚焦波的研究中,最高波面峰值与次高波面峰值能反映它与海洋结构物相互作用的激烈程度,本文通过修改参数,如Ga分别为0.002、0.01、0.018;水深分别为8 m、20 m、45 m生成波面过程,分析了最高波面峰值与次高波面峰值的比值变化。结果发现,最高波面峰值与次高波面峰值的比值变化与水深和Ga无关;最高波面峰值与次高波面峰值的比值与Δf/fc有关(图7)。从图7可以看出,不同其他参数情况下,最高波面峰值与次高波面峰值的比值随Δf/fc的变化一致;这个变化呈一定规律性,即当Δf/fc<0.81或Δf/fc>0.94时,最高波面峰值与次高波面峰值的比值随Δf/fc的增大而增大,当0.81<Δf/fc<0.94时,最高波面峰值与次高波面峰值的比值随Δf/fc的增大而减小。导致这一变化规律的原因可以从图5观察得知,Δf/fc<0.81时,聚焦波形相对比较规则,最高波面峰值与次高波面峰值的比值较小,最大值接近5,次高波面峰值出现的位置离最高波面峰值位置较近;当Δf/fc>0.94时,次高峰出现位置与最高峰位置的距离越来越远,两峰值之间有比较多的波面起伏,最高波面峰值与次高波面峰值的比值可以很大;在当0.81<Δf/fc<0.94时波形处于上述两种情况的过渡状态,最高波面峰值与次高波面峰值的比值在4~5之间。
2.2 高频情况
由于实验室波浪周期一般在0.5~3 s,水深相对较浅,选择聚焦波频率中值fc分别为0.33 Hz、0.7 Hz、1.1 Hz、1.5 Hz、2 Hz,水深分别为0.3 m、0.5 m、0.7 m、0.9 m、1.2 m等情况进行了计算、观察和分析。计算聚焦时间100 s、聚焦位置为0 m,组成波个数N为32。参数取值见表4。
图8是水深0.3 m时恒定陡度谱模型理论计算的波面时间过程,其他水深波形类似,只是幅值不同;图9给出不同水深情况下,最高波面峰值的变化;与低频聚焦波相似,当fc较小时(如0.33 Hz),最高波面峰值随水深增大显著增大;当fc较大时(如2 Hz),最高波面峰值随水深增大不明显;同一水深情况下,fc越小,最高波面峰值越大。最高波面峰值与次高波面峰值之比仍接近于1.58。
在高频时参数Ga范围与低频一致,在不同水深0.3 m、0.5 m、0.7 m、0.9 m、1.2 m下,进行了聚焦波波形计算。此时,聚焦时间100 s、聚焦位置为0 m,组成波个数N为32。计算中Δf/fc=0.5,其他参数见表5。
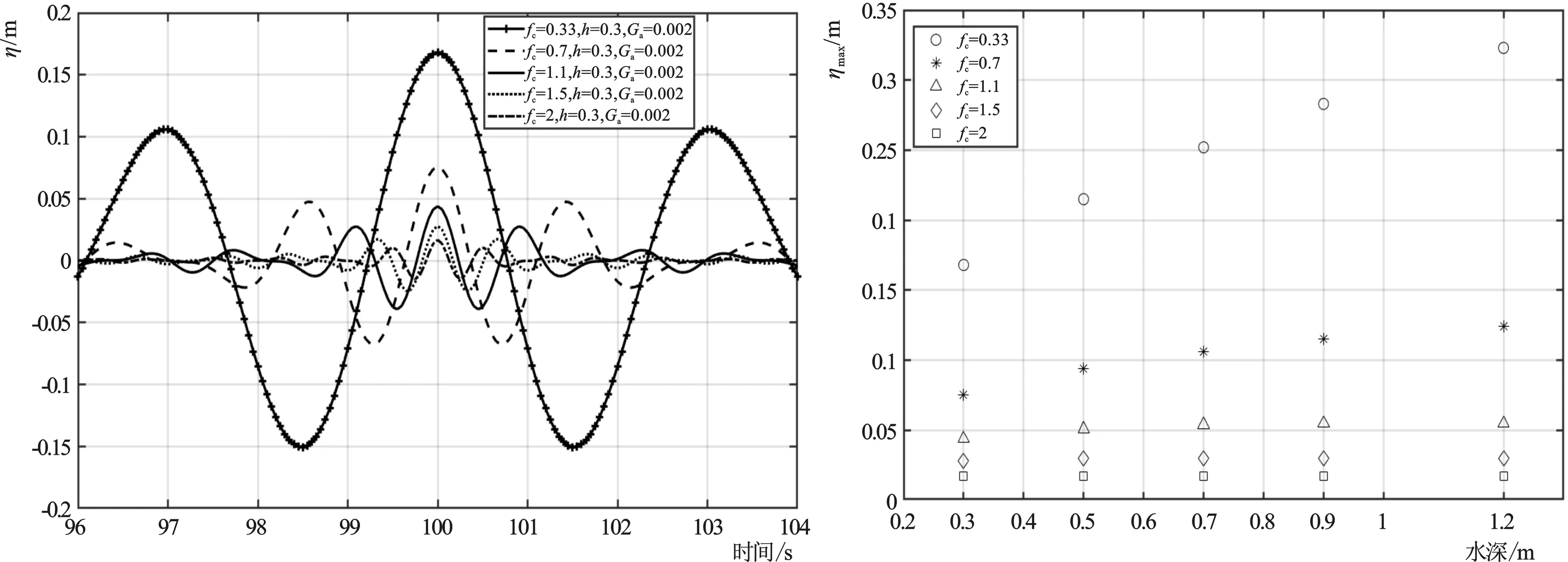
图8 不同fc的高频聚焦波波面过程线
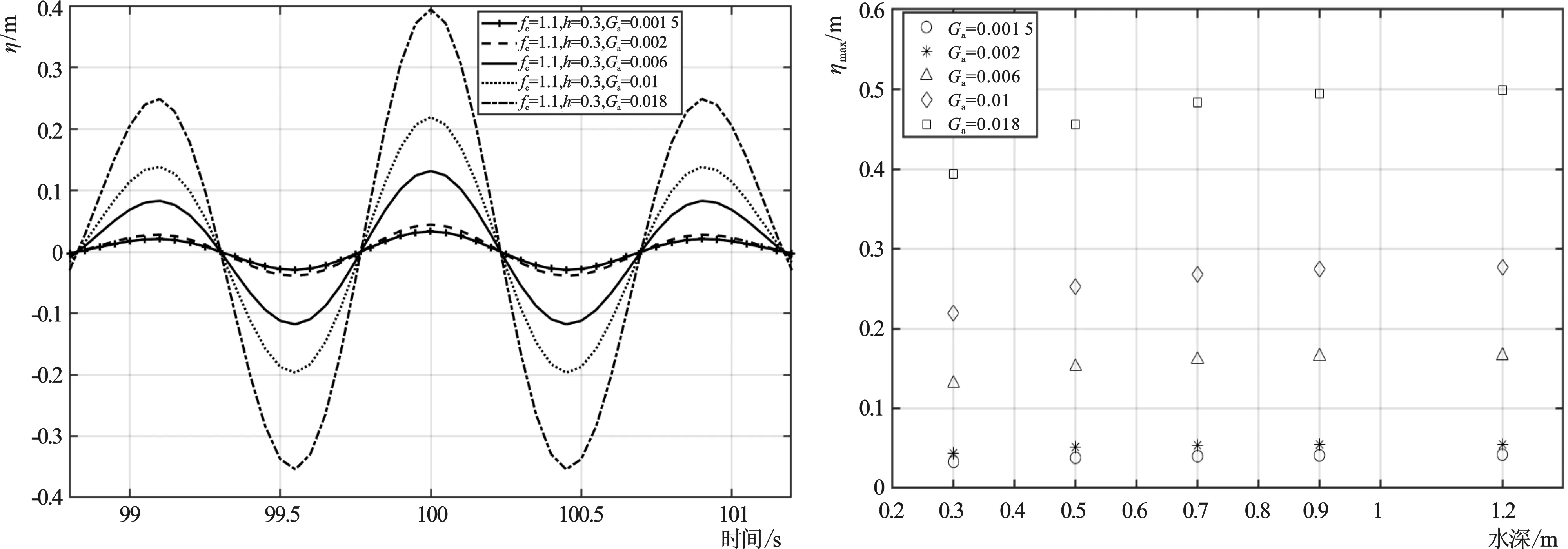
图10 不同Ga的高频聚焦波波面过程线
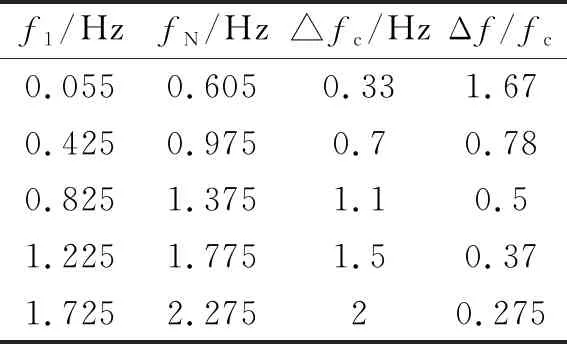
表6 不同Δf/fc的高频聚焦波参数
图10为计算的聚焦波波面时间过程线,同一水深情况下,Ga越大,最高波面峰值越大,这与低频情况下也一致。图11给出最高波面峰值与水深的关系,同一Ga情况下,水深越大,最高波面峰值越大;当Ga值较小(如0.002)时,最高波面峰值随水深增加不显著;而当Ga值较大(如0.018)时,最高波面峰值随水深增加显著增大。最高波面峰值与次高波面峰值之比仍接近1.58。
当Δf/fc在0.275~1.67变化时,Δf取0.55,Ga取0.002,其他参数见表6,fc分别为0.33 Hz、0.7 Hz、1.1 Hz、1.5 Hz、2 Hz。计算聚焦时间100 s、聚焦位置为0 m,组成波个数N为32,水深与前面高频组次相同。
图12为水深0.3 m时聚焦波波面过程线。与低频相似,当参数fc越小(如0.33 Hz),其波面最大峰值越高,波面变化越剧烈;fc越大(如2 Hz),波面最大峰值越低,最大峰值与次峰值离得越近。其他水位情况类似,只是最大峰值随水深增大而增大(图13)。
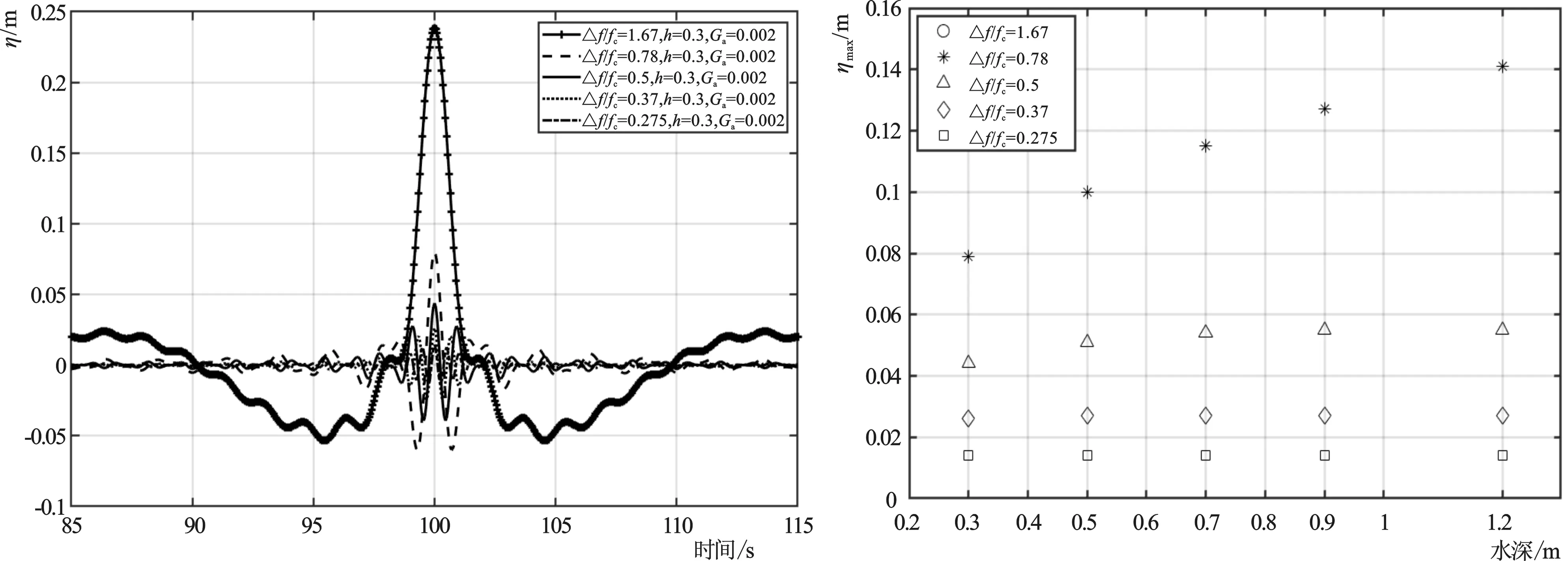
图12 不同Δf/fc的高频聚焦波波面过程线
最高波面峰与次高波面峰的比值变化与水深和Ga无关,与Δf/fc关系同低频情况一致见图7,这里不再赘述。
3 总结
本文分析了利用恒定陡度方式构建聚焦波的方法,分低频和高频两种情况,在不同频率、水深条件下,计算观察了波面形状,分析了最高峰值与次高峰值的比值。观察分析表明,无论高频和低频,最高波面峰值的变化为:当fc较小时最高波面峰值随水深增大显著增大;当fc较大时,最高波面峰值随水深增大不明显;同一水深情况下,fc越小,最高波面峰值越大。Ga越大,最大波面峰值越大。最高波面峰与次高波面峰的比值变化与水深和Ga无关;与Δf/fc有一定规律性,当Δf/fc<0.81或Δf/fc>0.94时,最高波面峰值与次高波面峰值的比值随Δf/fc的增大而增大,当0.81<Δf/fc<0.94时,最高波面峰值与次高波面峰值的比值随着Δf/fc的增大而减小。至于考虑波浪破碎的情况,有待进一步研究。
