采用数值计算和OrcaFlex软件对缆索张力函数的分析
2019-05-11张大朋白勇姬芬芬徐显明朱克强
张大朋,白勇,姬芬芬,徐显明,朱克强
1.浙江大学建工学院,浙江杭州 310058
2.青岛汉缆股份有限公司,山东青岛 266102
3.宁波大学海运学院,浙江宁波 315211
缆索已经被广泛应用于各种海洋工程中,如海洋系泊系统、深拖系统、ROV 系统[1-2]。缆索函数表征了缆索的形态,为缆索的设计和分析提供了直观的物理概念。由于缆索运动是非线性的,且作用于缆索上的流体动力也是随着时间不断变化的,所以它只能通过数值计算来近似求解[3]。本文分别运用数值计算的四阶龙格库塔法和OrcaFlex 软件的凝集质量法对缆索函数进行分析计算,得到两组不同流速下的曲线并对其进行了对比分析。
1 缆索的二维定常理论
规定缆索是匀质的,将其入水点看作上端,在船舶拖带下,以定常水平速度移动,缆索完全处于由水平运动方向和垂直方向构成的平面内。缆索的自由端连接被拖物体,受到定常作用力[4]。为计算方便做了以下3 点假设:其一,缆索是完全挠性的,只有缆索张力;其二,作用于缆索某一单元的水动作用力,仅取决于该缆索元相对于流的角度;其三,不受相邻缆索元影响,拖曳缆索时的自由面影响可以忽略。
作用于微元上的外力必须与微元两端所受的内部张力平衡,其中外力包括水动作用力和重力,设P(φ)和Q(φ)为外力沿缆索元长度在切向和垂向方向上的分量,T 为缆索的轴向张力;φ 为缆索元与水平方向的夹角;s为缆索元轴向方向的长度。力的平衡关系见图1。

图1 缆索元的受力分析
可以得到,缆索元在长度方向上缆索角和张力的变化为:

如图2 所示,为方便选取坐标系,由原点至缆索的任一点积分可以得到某一点处的张力,但是实际做法是从原点开始积分较为方便,原点上的缆索角已知为90°,设该处的张力Δ1为已知,可以得到点(x,z)处的张力T:


图2 缆索坐标系
设R 为缆索元所受的阻力。当R 垂直于流时,可以得到上述积分的无因次形式:
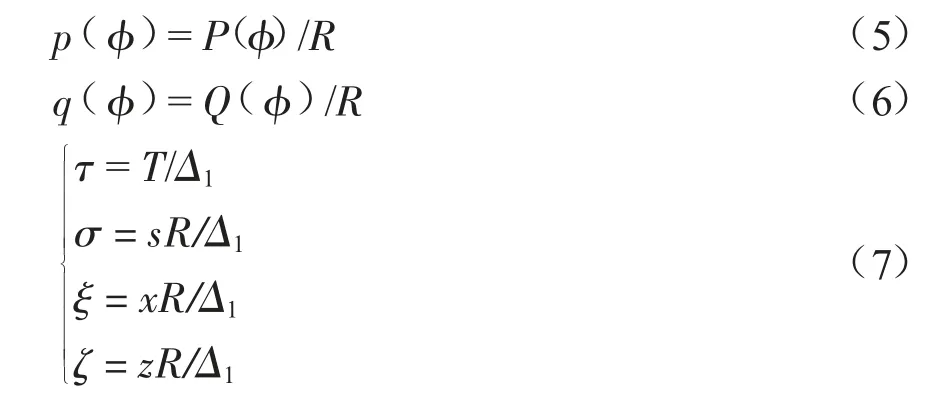
式中:τ 为张力函数。
2 确定缆索函数的一种实用方法
缆索分为轻型缆索和重型缆索,当水中重力W 远小于流体阻力R 时,为轻型缆索;反之,则为重型缆索。μ 为摩擦系数,当其值为1时,阻力完全由缆索与水的摩擦效应产生,这时称缆索接近理想状态。对于重型缆,除了摩擦系数μ 为1 的理想状态外,其他情况必须借助数值计算才能得到缆索张力函数,缆索元作用力分量示意如图3 所示,G(φ)、F(φ)为外力沿缆索元长度在切向和垂向的分量。

图3 缆索元作用力分量
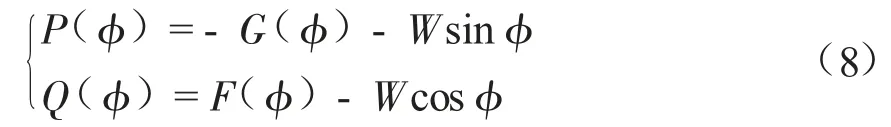
其无因次形式为:
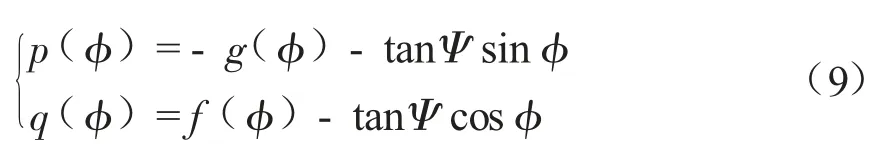
式中:f(φ)=F(φ)/R、g(φ)=G(φ)/R 均为无因次流体动力载荷系数;Ψ 为重力角,可定义为:

式中:W 为缆索元的水中重力。

式中:CR为阻力系数,ρ 为水的密度,d 为缆索直径,V 为对流速度。
假定摩擦阻力不受压力分布的影响,它的作用力方向与流向一致,与缆索角无关。这样载荷函数可记为:
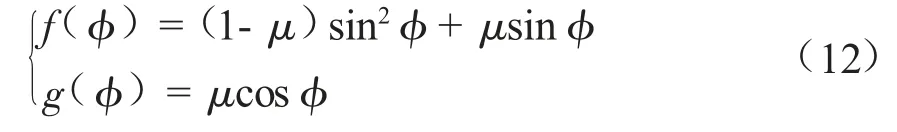
不同的缆索与水接触所产生的摩擦力不同,摩擦力的大小与摩擦系数μ 相关。典型缆索的CR和μ 值如表1 所示。

表1 典型缆索的CR 和μ 值
对于重型缆而言,除了μ=1 的理想状态外,必须借助数值积分才能求得缆索函数。已知张力函数为:
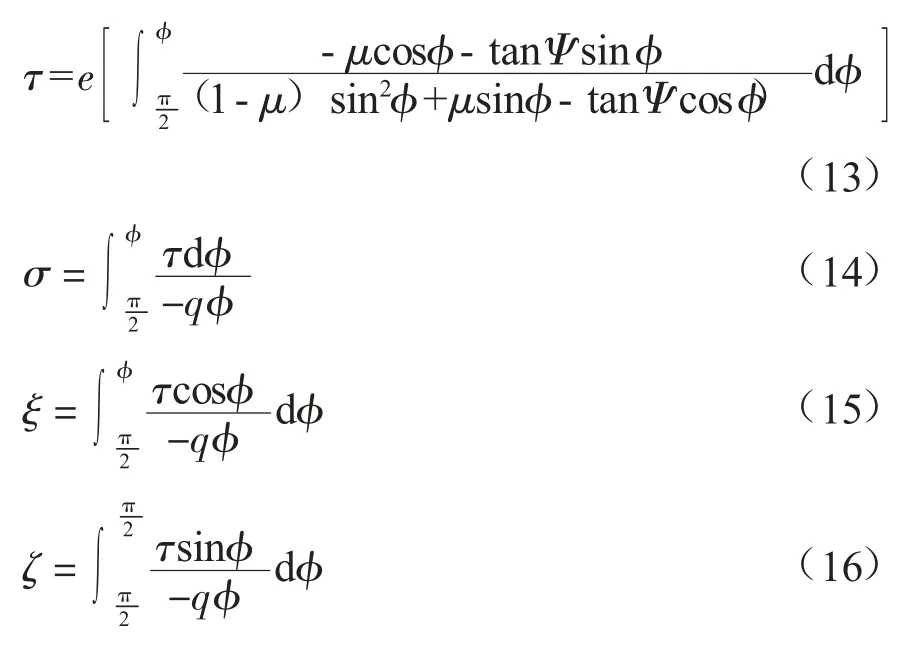
令μ=0.5,用四阶龙格库塔法分别计算重力角Ψ 等于2°、4°、6°、8°和10°时的张力函数,结果见图4。

图4 重型缆索的张力函数
当重力角一定时,张力函数在缆索角较小时曲线较陡,但随着缆索角的增加曲线越来越平缓,最后在缆索角为90°时曲线值趋近1。当缆索角一定时,重力角越大张力函数曲线就越陡,如图4 所示,当重力角增大时,曲线会变得越来越陡。当摩擦系数一定时,重力角越大张力函数值就越大。
3 缆索函数分析
3.1 案例分析
缆索模型示意如图5 所示。

图5 缆索模型示意
缆索:直径d=0.012 m,单位长度质量m=0.132 kg/m,轴向阻力系数Cn=1.2,切向阻力系数Ct=0.007 6,拖船速度V=2 m/s,缆索摩擦系数μ=0.05。
拖体:为规则的圆柱形状,圆柱高=1 m,体积=0.61 m3,质量=700 kg。
模型:用悬链线模拟缆索,用3D 浮标单元模拟拖体。采用凝集质量法进行建模,把缆索视为有限个微段,每个微段的质量和流体作用力等均凝集在使用线性或非线性弹簧连接的节点上[5]。被离散为凝集质量模型的缆索[6]由若干个分段和节点组成,其中分段为连续、无质量的,节点处于各分段终点处且集中了两个相邻分段各一半的质量,力和力矩都作用于节点上,这也正是OrcaFlex 软件对缆索张力建立模型的数学基础[7-12]。
在确定φ0后,在某一p(φ)及q(φ)分布下,可求得与物体相连点上缆索张力函数,于是原点处的张力Δ1=T0/τ0。不同流速下数值计算与OrcaFlex 模拟结果的对比见图6。缆索角越小,两条曲线的契合度越低;但随着缆索角的增加,两种方法计算得出来的曲线契合度越高。如图6 所示,在一定流速下随着缆索角的增加,两种方法所得曲线间差值越来越小,当缆索角在1.1 ~1.2 rad 时,差值最小,两曲线的契合度达到最高。
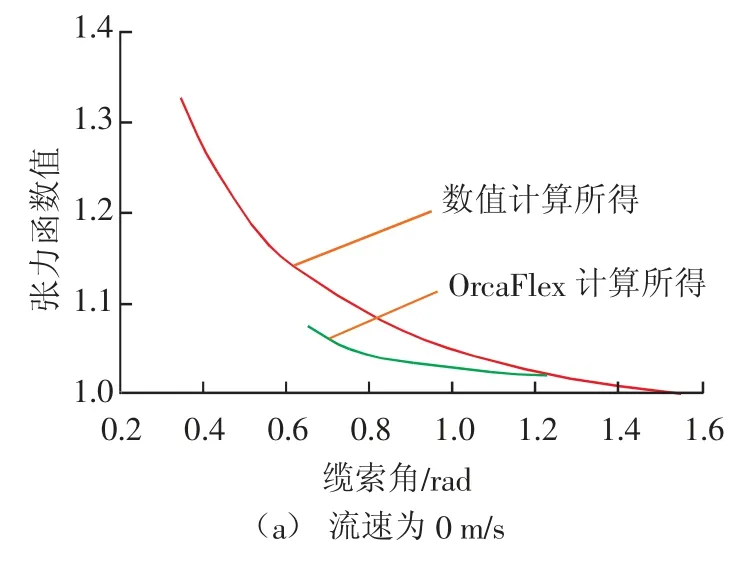

图6 不同流速下数值计算与OrcaFlex 模拟结果对比
随着流速的增加,两条曲线的契合度增加;当流速为1 m/s、缆索角为0.6 rad 时,两曲线差值为0.021;当流速为0 m/s、缆索角为0.6 rad 时,两曲线值差值为0.064。所以,当流速越大时用OrcaFlex 模拟得到的张力函数曲线与数值计算得到的曲线更为接近。由图6 可以看出,数值计算和软件模拟误差很小,所以OrcaFlex 软件能够代替数值计算来模拟缆索函数。
图6 所示的数值计算和OrcaFlex 模拟所得的缆索角范围不同,这是由于数值计算是为了计算简便将缆索反向延长得到最大缆索角为90°(1.57 rad),这时由原点至缆索的任一点积分可以得到某一点处的张力,但是实际做法是从原点开始积分较为方便。同时又能把缆索延长,得到最小缆索角。为了尽可能地把实际缆索角包络在内,最小缆索角设定为0.35 rad。也就是说数值计算就是得到一条范围尽可能大的张力函数曲线,然后再确定最小缆索角和最大缆索角。
3.2 缆索函数的用途
缆索函数完全规定了缆索的形态,对给定的缆索作用力分布可按数值积分求值。分析缆索系统的实际做法可归纳成下列过程。
缆索的一些特征是已知的,如缆索直径d、单位长度缆索的水中重力W、垂向阻力系数CR等,给定的拖速下,被拖物体的垂向力和阻力可以用Morison 方程估算得到。在确定φ0后,在p(φ)及q(φ)分布下,可以得到与物体相连的点上缆索函数值τ0、σ0、ξ0和ζ0,于是原点处的张力:

式中:T20=Δ2+D2,cot φ0=D/Δ,T0为与物体相连点处的张力;Δ 为拖体的垂向力;D 为阻力。可以求得拖体相对于原点的位置,如(s0,x0,z0)。
因此,在给定的计算状态的情况下,可以确定缆索的几何形状和张力及拖体相对于原点的位置。
4 结论
(1)可以用OrcaFlex 软件解决缆索张力函数问题,避免了复杂的数值计算。
(2)在摩擦系数一定时,重力角越大张力函数值就越大,因此在实际工程中适当减小缆索的重力可以减小缆索张力,这对实际生产具有很大的参考意义。
(3)缆索函数可为缆索的设计和分析提供直观的物理概念,而OrcaFlex 软件可以较为准确地模拟缆索函数,所以在工程实践中可以运用OrcaFlex 软件对缆索进行设计和分析。
(4)缆索函数可表征拖体和缆索的特性,且可预测拖曳的性能。
