SHPB入射波相似律与整形技术的试验与数值研究
2022-03-27王江波李汶峰任文科王晓东李继亮高光发
王江波, 李汶峰, 任文科, 王晓东, 李继亮, 高光发
(南京理工大学 机械工程学院,南京 210094)
分离式霍普金森压杆(split Hopkinson pressure bar,SHPB)[1]自从建立以来,被广泛应用于混凝土[2]、陶瓷[3]、金属[4]、岩石[5]、复合材料[6]、聚合物[7-8]和泡沫材料[9]等的动态力学响应测试,可获得材料在102~104s-1应变率范围内的应力应变曲线。为了确保试验结果的准确性,试验过程中需要满足恒应变率加载及试件内部应力均匀等基本条件。
在大多数情况下,常规的梯形入射脉冲无法满足恒应变率变形的要求,同时还会产生一系列高频分量的应力波,每一个频率分量的应力波在传播时由于速度不同,会导致入射波形发生弥散效应[10],这种现象不仅会影响试验时的动态应力平衡,而且有可能会掩盖材料本身的力学特性。因此,为了能得到更准确的试验数据,需要对入射波的波形进行修正,研究表明主要有改变撞击杆的形状[11]、使用预加载杆技术和脉冲整形器技术[12]。由于前两种方法有很多弊端如撞击杆形状加工困难、很难实现恒应变率加载等,所以波形整形器就成为应用最广泛的脉冲整形技术,它是通过对入射波形的调整来改变反射波形,其原理是在撞击杆和入射杆端面之间放置一个片状材料,只要选取适当的材料和尺寸,就可以最大程度减小SHPB试验中波形的弥散效应,同时可以实现动态应力平衡和恒应变率加载等要求。
由于波形整形器使用简单,能对入射波形进行有效的整形,故很多学者都对此进行了研究。Frew等[13-14]基于材料体积不可压缩和均匀变形理论,得到了整形器的分析模型,并利用整形器技术进行了岩石、玻璃陶瓷和钢的SHPB试验,结果表明,使用整形器后,试件处于动态应力平衡状态,试验的大多数时间具有恒定的应变率,还可以通过调整整形器尺寸控制入射波的上升持续时间,分析模型与试验结果一致,同时还可以预测试件应力平衡和恒应变率持续时间。Naghdabadi等[15]进行了整形器对入射波影响规律的试验研究和数值仿真,给出了不同材料SHPB试验时整形器尺寸的选择准则。Bagher Shemirani 等[16]使用紫铜整形器进行了混凝土材料的SHPB杆试验,并对试验过程中动态应力平衡、恒应变率状态进行了分析,并且给出撞击杆长度和速度对入射波形的影响规律。
从以上分析可知,学者们只是针对某一口径SHPB装置或特定材料进行了整形器对入射波构形的影响规律研究,而关于使用整形器的入射波构形是否满足相似律的研究未曾出现。研究此问题可将不同杆径SHPB装置的入射波整形技术及理论进行统一,并且对新型SHPB装置的设计具有非常重要的科学意义。基于此,本文利用量纲分析理论研究了使用整形器的SHPB入射波形构形是否满足严格的几何相似律,并根据试验和数值模拟结果对此进行了验证,然后基于直径为14.5 mm的SHPB装置研究了整形器直径、厚度以及撞击杆长度和速度对入射波形的影响规律,最后,通过对各影响因素的定量分析,得到了对入射波构形的两个重要拐点T1和T2的无量纲表达式。
1 量纲分析
整形器为紫铜材料,由于在试验过程中整形器的塑性应变远大于弹性应变,加载过程中整形器的弹性加载时间远小于塑性加载时间,因此在量纲分析中不考虑整形器的弹性阶段,即可以忽略整形器的杨氏模量和泊松比,则其应力应变曲线可以近似等效为线性硬化模型。设整形器的塑性硬化模量为E0,屈服强度为σs,密度为ρs,厚度为h,直径为d。假设SHPB装置杆直径为Db,撞击杆长度为Lb,撞击速度为v,密度为ρb,杨氏模量为Eb。当SHPB杆装置的长度远大于直径时,我们可认为其满足一维应力假设,故可以不考虑杆材料的泊松比。因此,我们可以给出入射杆中测量点截面上的应力函数表达式
σ=f(Eb,ρb,Lb,Db;E0,σs,ρs,h,d;v,t)
(1)
基于量纲分析理论,我们选择质量(M),长度(L)和时间(T)作为基本量纲,式(1)中所有参数的量纲列于表1中。
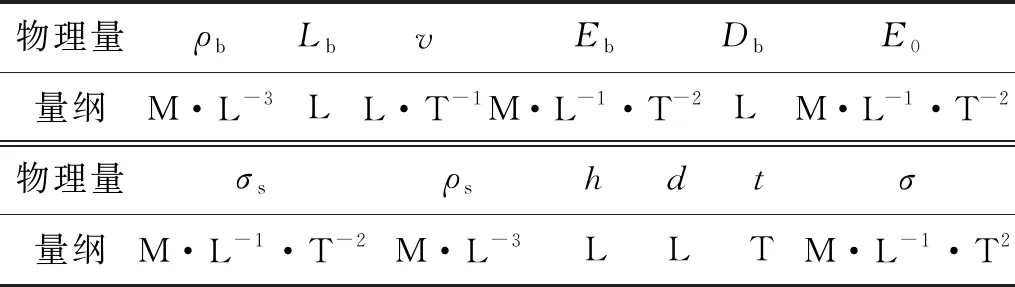
表1 杆和整形器参数的量纲
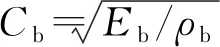
(2)
如果没有使用整形器时,撞击杆的直径和撞击速度对无量纲应力并无影响,可以忽略式(2)中与整形器参数无关的前两项,同时由于整形器的厚度很小,不考虑应力波在整形器中的传播时间,即忽略整形器的惯性效应,则可以不考虑密度的影响,则可以得到
(3)
式中:σ*=ρbCbv/2;t*=Lb/Cb。缩比模型中杆材料和整形器与原模型相同时,即可得到
(4)
式中:下标m为原模型;p为缩比模型。
因此,对于撞击杆速度v相同时,要使使用整形器的SHPB入射波构形满足几何相似律,则必须有
(5)
2 试验研究和数值模拟
2.1 试验方法
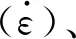
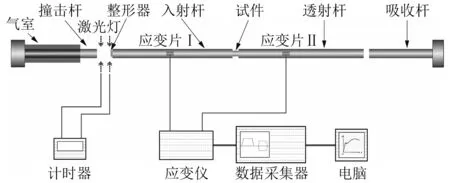
图1 SHPB装置系统示意图
(6)
式中:Ab为杆的横截面积;As和Ls为试件的横截面积和长度
为了验证SHPB装置的相似律问题,以及后续研究整形器对入射波形的影响规律,试验选用常用直径为14.5 mm的SHPB装置,该装置撞击杆、入射杆和透射杆的规格尺寸,如表2所示。

表2 SHPB装置中杆的尺寸和材料
整形器材料的选取与待测试件材料的性能相关,一般选用紫铜、黄铜等材料,在加载过程中其应力应变关系可以近似为线性硬化模型。本文主要针对金属、高聚物等一些延性材料SHPB试验时整形器尺寸的选取进行研究。采用合适材料和尺寸的整形器不仅可以减小试验过程中波形弥散对试验结果的影响,而且可以实现试件内部的动态应力平衡和试验过程中的恒应变率加载。
2.2 数值模拟模型
2.2.1 整形器材料力学参数
选取T2紫铜作为整形器材料,为了整形器仿真材料模型的准确性,对紫铜材料进行了准静态压缩试验。紫铜试件准静态压缩的应力应变曲线,如图2所示。根据相关标准可以测得其屈服强度、杨氏模量、以及塑性切线模量,同时利用密度计测量了其密度,如表3所示。
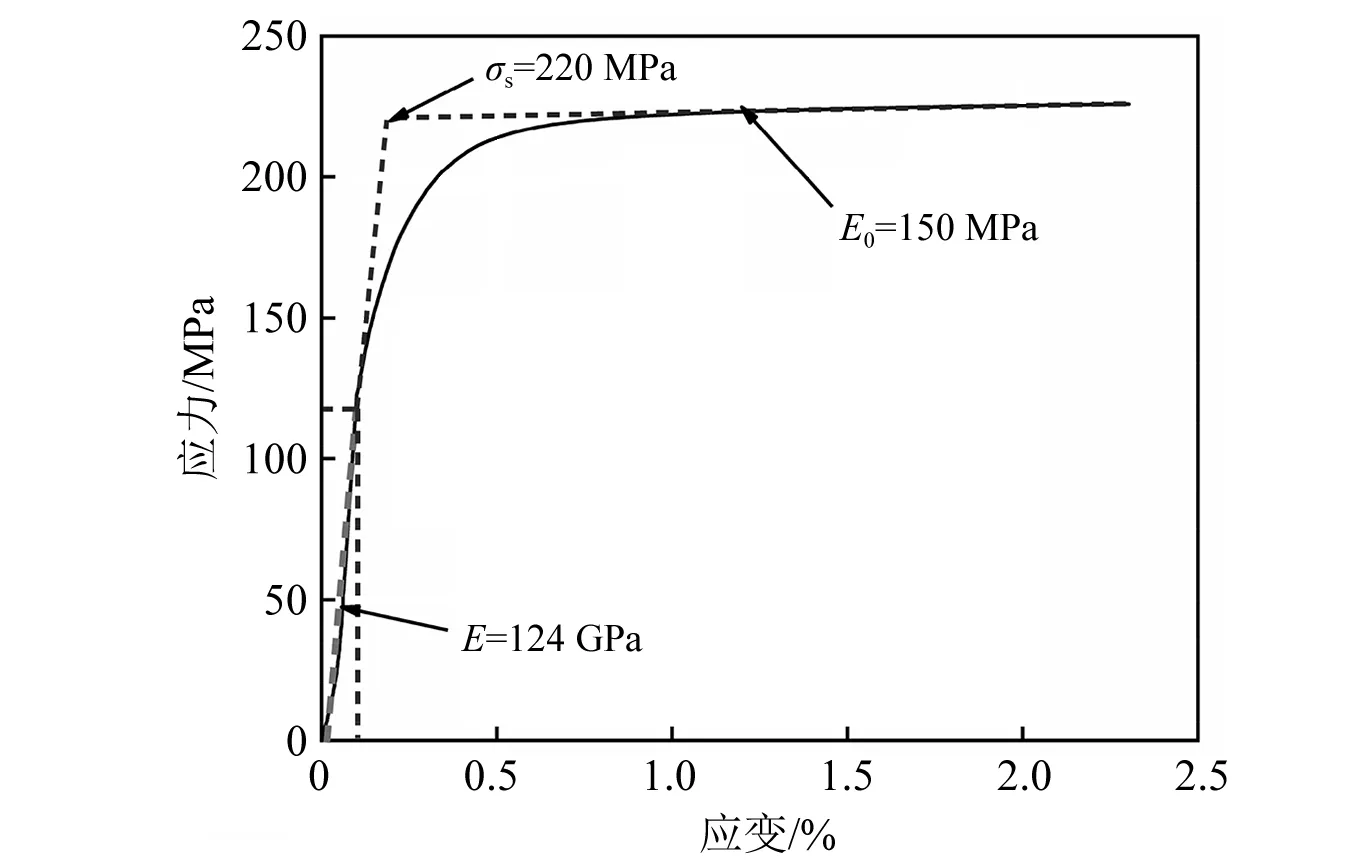
图2 紫铜材料应力应变曲线及各参数的计算

表3 紫铜整形器的主要力学参数
2.2.2 数值仿真几何模型
利用有限元软件ABAQUS对使用整形器的SHPB试验进行了数值仿真,模型包括撞击杆、整形器和入射杆。本文主要研究整形器对入射波的影响规律,故在建模过程中忽略了透射杆。由于整形器尺寸较小,为了保证杆与整形器接触端网格尺寸相匹配,杆的有限元模型采用过渡网格划分方法。因此杆的仿真模型包括细化网格区(Ⅰ)、过渡网格区(Ⅱ)和粗化网格区(Ⅲ)。
以直径为14.5 mm的SHPB装置为例,其有限元模型如图3所示。模型中细化网格区域长度为30 mm,过渡网格区域长度为20 mm。同时,为了排除网格尺寸对数值模拟结果的影响,细化区的网格为边长为0.1 mm的正方形,过渡区网格为边长为0.725 mm的正三角形,粗化区网格为0.725 mm×1.450 mm的长方形。

图3 ABAQUS软件中模型的建立及网格的划分
在整个试验过程杆始终处于弹性状态,因此数值仿真模型中入射杆和撞击杆采用弹性模型,其主要参数如表4所示(整形器材料采用双线性模型,其主要参数已列于表3)。

表4 仿真模型中杆材料的力学参数
根据文献[17]对铜试件SHPB研究中界面摩擦因数的研究并对此进行了微调,整形片与撞击杆接触的一端未添加润滑剂,数值仿真中设置摩擦因数为0.12;而整形片另一端与入射杆通过润滑剂粘住,摩擦系数为0.03,同时对无整形器SHPB试验也进行了数值仿真,模型中各部分的接触定义为面-面接触。有无整形片试验与仿真的对比图,如图4所示。从图4可知,两者之间有着很好的重复性,因此可以说明仿真模型和材料参数是准确可靠的。

图4 撞击杆速度为16 m/s时有无整形器的入射波形试验和仿真对比图
3 SHPB试验入射波相似律的验证
为了验证量纲分析中SHPB试验的几何相似性,基于直径为14.5 mm的SHPB装置,开展了不同缩比尺寸的SHPB试验和数值仿真研究,具体方案如表5所示。原模型中(几何缩比为1)撞击杆长度为400 mm,整形器的厚度为0.8 mm,直径为8 mm,缩比模型与原模型材料相同且撞击杆速度也相同为16 m/s,几何缩比分别为1.5和0.5。

表5 SHPB装置的缩比试验与数值仿真几何参数
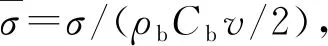
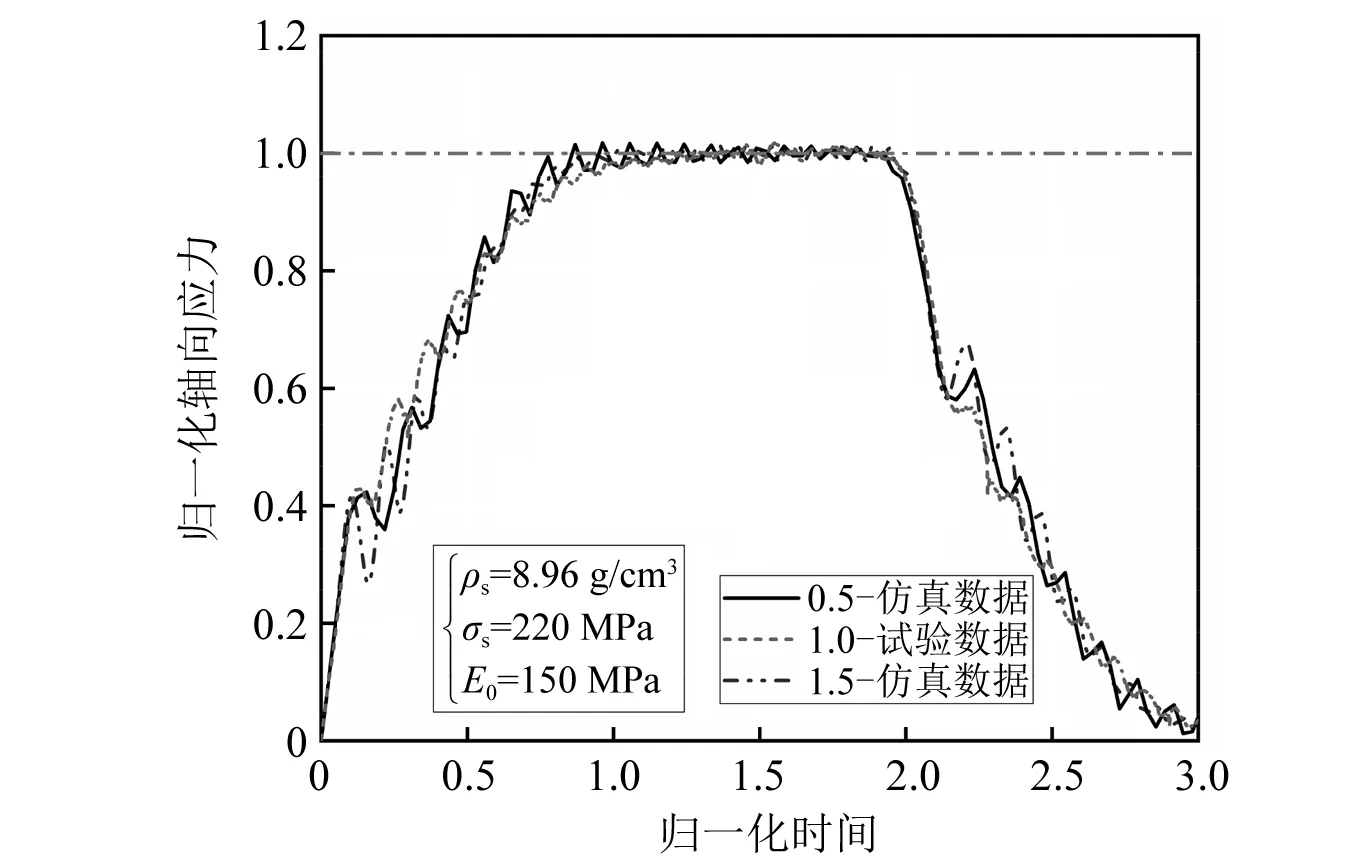
图5 SHPB试验中入射波的几何相似性试验与数值仿真结果
根据SHPB试验相似律量纲分析的结果和图5中不同缩比模型的入射波形,当原型中杆和整形器材料与缩比模型完全相同,且撞击速度相同时,入射波的无量纲正应力与无量纲时间之间的关系图即无量纲入射波形基本相同,说明考虑整形器的SHPB试验满足几何相似律,同时验证了量纲分析的准确性。因此,当不同直径的装置满足SHPB试验中的两个基本假设后,后续研究整形器对入射波的影响规律可以适用于任何口径的SHPB装置。
4 整形器和撞击杆参数对入射波形的影响
对于入射波的整形问题,一般只考虑加载阶段,波形的卸载部分对试验基本没有影响,因此可以不考虑入射波形卸载部分。SHPB试验中有无整形器典型的入射波形,如图6所示。从图6可知,我们可以发现,使用整形器的入射波形可以分成两个关键节点和三个加载区域,分别为:Ⅰ.弹性加载区域,即试验时整形器处于弹性变形的阶段;Ⅱ.塑性加载区域,即试验时整形器为塑性变形的阶段;Ⅲ.刚性加载区域,即整形器完全塑性变形后直至波形加载结束。
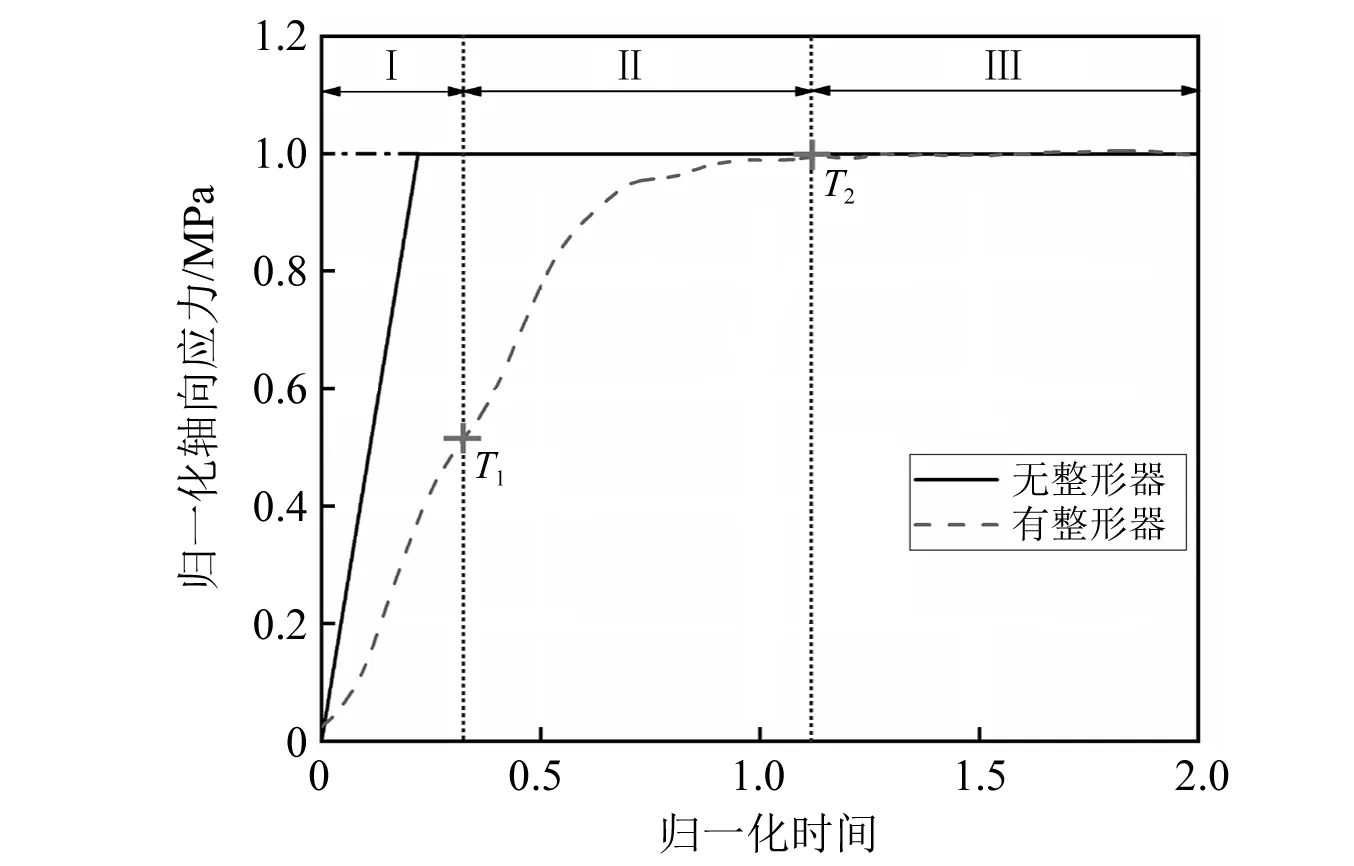
图6 入射波形中的关键拐点和加载区域
由于脉冲整形技术中影响入射波构形的因素较多以及试验时所处应力场的复杂状况,所以很难给出整形后入射波形的具体方程式。因此,本文根据整形器在其工作时所处的应力应变状态,对其尺寸对入射波构形两个重要拐点T1和T2的影响规律进行了具体分析。事实上,整形器对入射波构形的整形就是改变T1和T2拐点的位置以及两拐点之间曲线的形状(见图6中Ⅱ区域),然后根据待测试件的力学性能调整入射波的构形使试验在恒应变率加载下进行。然而,图6中Ⅱ区域波形很难给出具体的表达式,故我们对其起点和终点进行了具体的分析,为SHPB试验时整形器的选取提供一定的参考作用。
当考虑某个影响因素对入射波某一点无量纲应力的影响时,可以忽略掉变量时间的影响,因此,类似于第1章中的量纲分析,我们得到入射波特定点的无量纲应力表达式为
(7)
后续研究中针对式(7)中各因素对入射波两个拐点T1和T2的影响进行了具体的分析。
4.1 整形器直径对入射波形的影响
基于直径为14.5 mm的SHPB装置,进行了一系列不同直径整形器的SHPB试验和数值仿真。其中,撞击杆的速度为16 m/s,撞击杆长度为400 mm,整形器的厚度为0.8 mm。SHPB试验中使用不同整形器直径时的入射波形图,如图7所示。
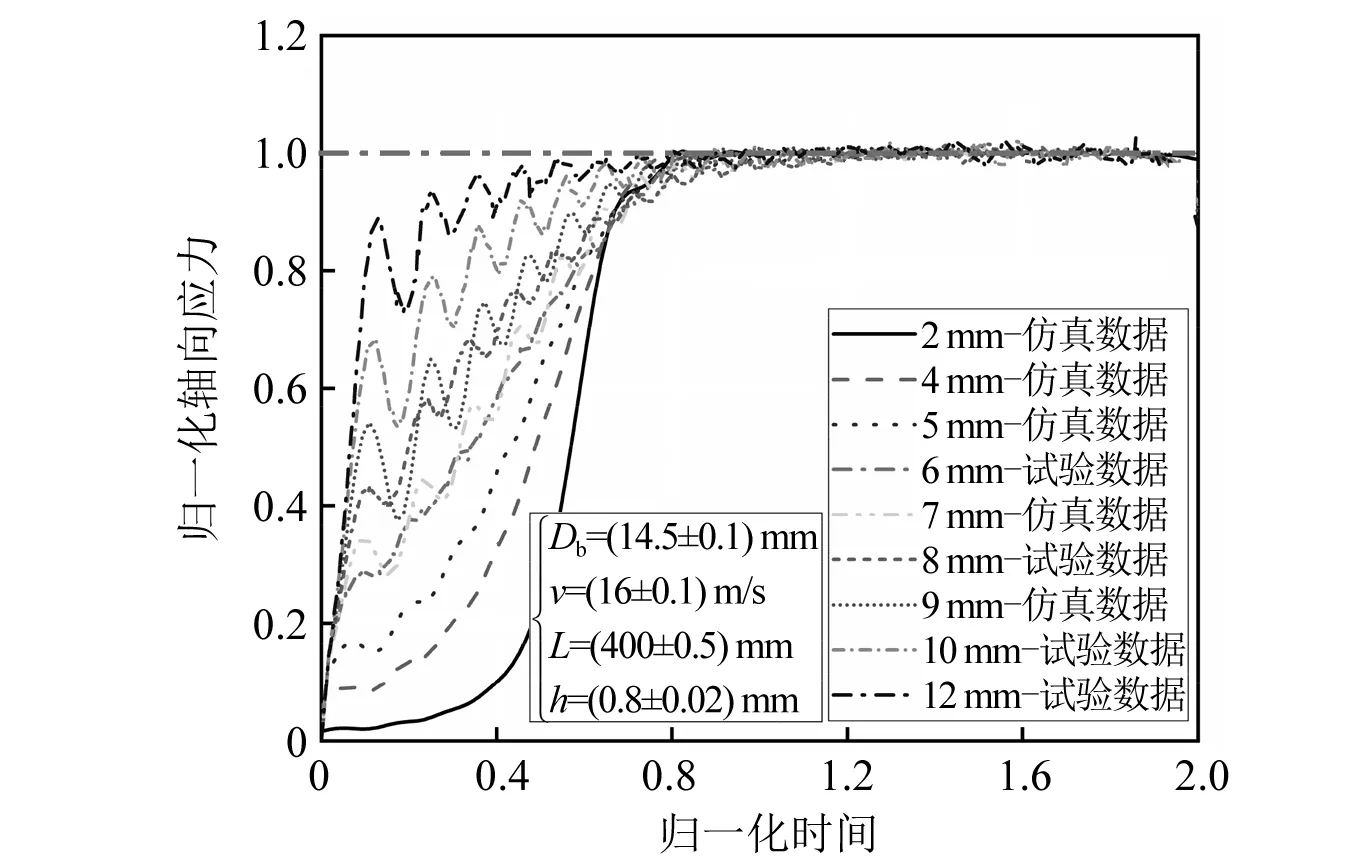
图7 不同整形器直径对应的入射波形图
从图7可知,当整形器厚度和撞击杆速度不变时,入射波的T1拐点随着整形器直径的增大而增大,这是由于随着整形器直径的增大,整形器压缩过程中到达其屈服点时的面积也随之增大,而在加载过程中,整形器和杆端面的轴向力相等,所以导致入射波的T1拐点无量纲应力逐渐增大,同时T1拐点对应的无量纲时间也变大;但整形器直径对T2拐点没有明显的影响,即整形器直径主要影响塑性加载区域Ⅱ的起始点,对其终点没有影响。
4.2 整形器厚度对入射波形的影响
为了分析整形器厚度对入射波形的影响,开展了不同整形器厚度的SHPB试验和数值仿真,整形器的直径为8 mm,撞击杆长度和速度同4.1节,试验和数值仿真结果如图8所示。
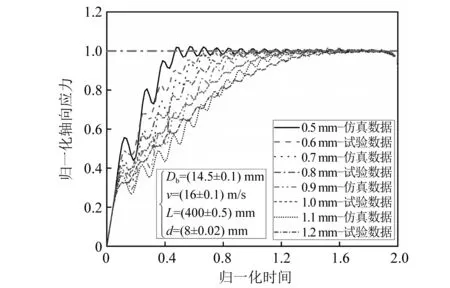
图8 不同整形器厚度对应的入射波形
当整形器厚度从0.5 mm增加到1.2 mm时,入射波形的T1拐点无量纲应力和无量纲时间也随之减小,这是由于压缩过程中整形器到达屈服点(入射波形的T1拐点)时,整形器的厚度越大,其对应的当前横截面积越小,又因为试验过程中整形器和入射杆轴向力相等,故导致T1拐点无量纲应力降低。而T2拐点的无量纲时间随着整形器厚度的增加逐渐增大,波形的塑性加载上升沿逐渐变缓,其原因是整形器在受压过程中为均匀变形,随着厚度的增加,其达到整形器完全塑性变形时所需的时间更长,故会导致入射波形的上升沿时间变长,即T2拐点右移。
4.3 撞击杆长度对入射波形的影响
在SHPB试验中,入射波的脉冲持续时间与撞击杆的长度有关,为研究撞击长度对入射波形的影响,进行了不同撞击杆长度的SHPB试验与数值模拟,其中撞击杆速度为16m/s,整形器直径和厚度分别为8 mm和0.8 mm,数值仿真和试验结果如图9所示。
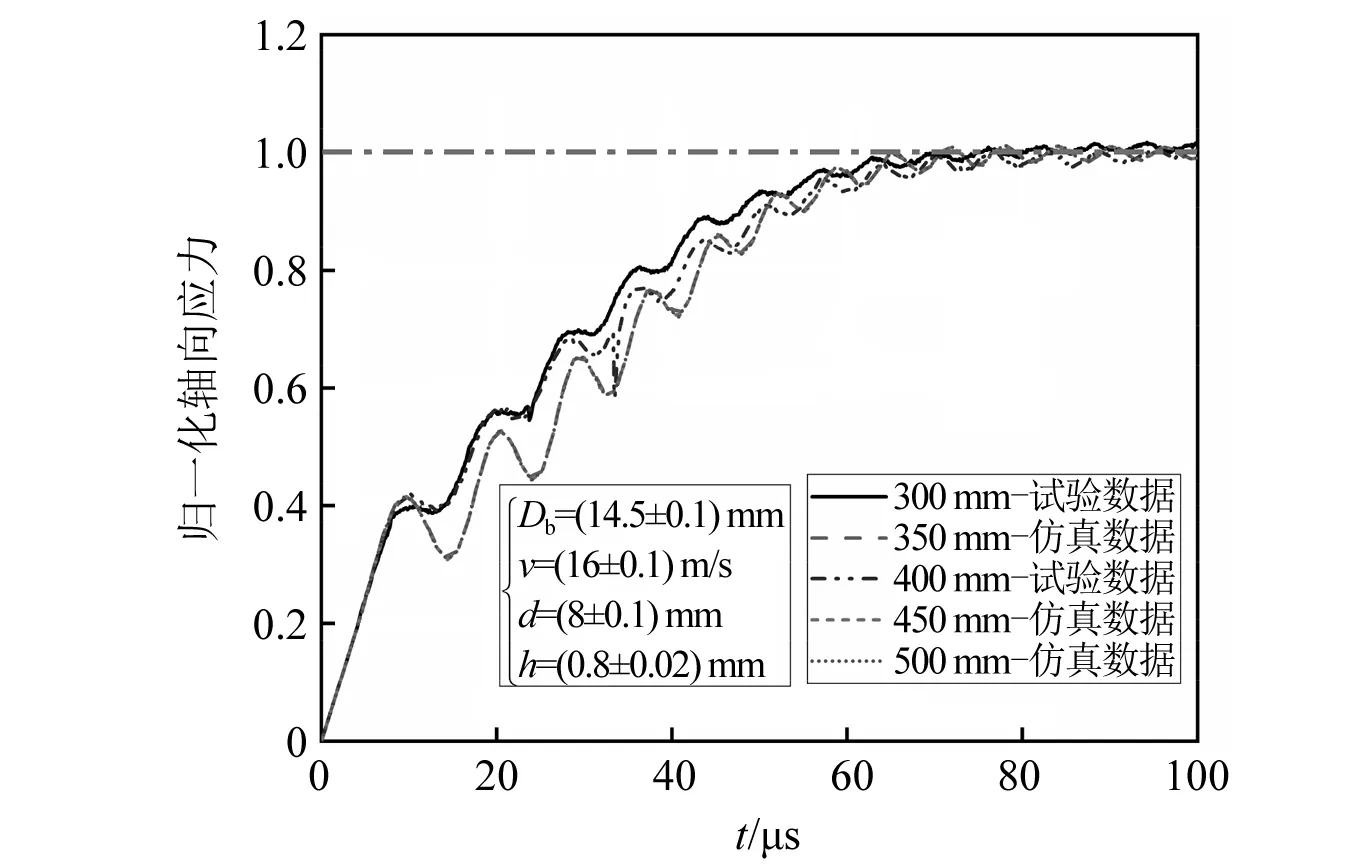
图9 不同撞击杆长度的入射波形
从图9可知,当撞击杆的能量足够大时,即入射波形存在刚性加载区域Ⅲ,整个上升沿阶段不同撞击杆长度的入射波形基本一致,不同撞击杆长度下的弹性加载区域Ⅰ和塑性加载区域Ⅱ重合,故当撞击杆动能足够时,撞击杆长度对入射波的两个关键拐点T1和T2没有影响,也就是说,撞击杆长度对于整形器的整形可以忽略。而当撞击杆动能较小时,入射波应力未达到理论应力峰值就会出现卸载情况,但对于整形器尺寸和撞击杆速度相同而撞击杆长度不同对应的入射波,其波形与存在刚性加载区域的入射波形加载区域Ⅰ和Ⅱ重合,这与Naghdabadi研究中的结论一致。
4.4 撞击杆速度对入射波形的影响
SHPB试验中撞击杆的速度对试件的应变率有着直接的影响,一般来说,撞击杆的速度越大,试验时的应变率就越高,故研究撞击速度对入射波整形规律的影响就显得很重要,撞击速度分别为8~20 m/s时对应的入射波形,如图10所示。其中整形器的直径和厚度保持不变,分别为8 mm和0.8 mm,撞击杆的长度为400 mm。
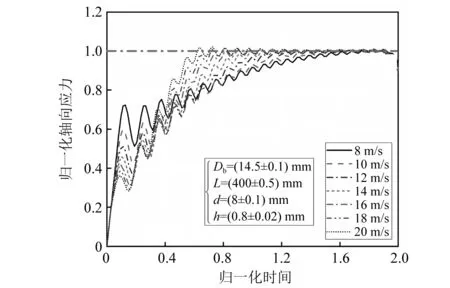
图10 不同撞击杆速度对应的波形图
根据波动力学理论,不同撞击速度的入射波应力峰值为σ*=ρbCbv/2,即随着撞击速度的增加,入射波的应力峰值也逐渐增大。对入射波形进行无量纲化后,随着撞击速度的增大,入射波形的T1拐点的无量纲应力逐渐减小(见图10),这是由于在对应力进行无量纲化时除以理论应力峰值导致的,实际上入射波T1点应力值大致相等;入射波形的T2拐点的无量纲时间随着撞击速度的增大逐渐减小,主要原因是因为撞击速度高时导致整形器的变形速率加快,导致其完全塑性变形的时间减小,故T2拐点的无量纲时间逐渐减小。
4.5 T1拐点的定量分析
对于入射波形T1拐点的取法,具体如下:根据图4中试验和仿真的对比结果可知,两个波形在T1点附近的交叉点约为入射波形第一个波动部分的中点,故为了统一试验和仿真中T1点的取法,统一采用入射波形第一个震荡部分的中点为T1点。根据4.1节~4.4节的分析可知,整形器的直径和厚度以及撞击杆的速度都会对T1拐点有一定的影响,而撞击杆的长度对其没有影响,同时,假设式(6)中的三个影响因素σs/σ*,d/Db,h/Lb,是相互解耦的,则式(7)可以变为
(8)
因此,为了得到T1拐点的无量纲应力表达式,根据图7、图8和图10得到了入射波形的T1拐点的无量纲应力与各无量纲参数的对应关系,如图11所示。从图11可知,T1拐点的无量纲应力σs/σ*与无量纲直径d/Db呈二次函数关系,与速度有关项σs/σ*和整形器无量纲厚度呈线性关系,因此我们对此分别进行了多项式和线性拟合,可以得到T1拐点的无量纲应力表达式为(0<σ/σ*<1)
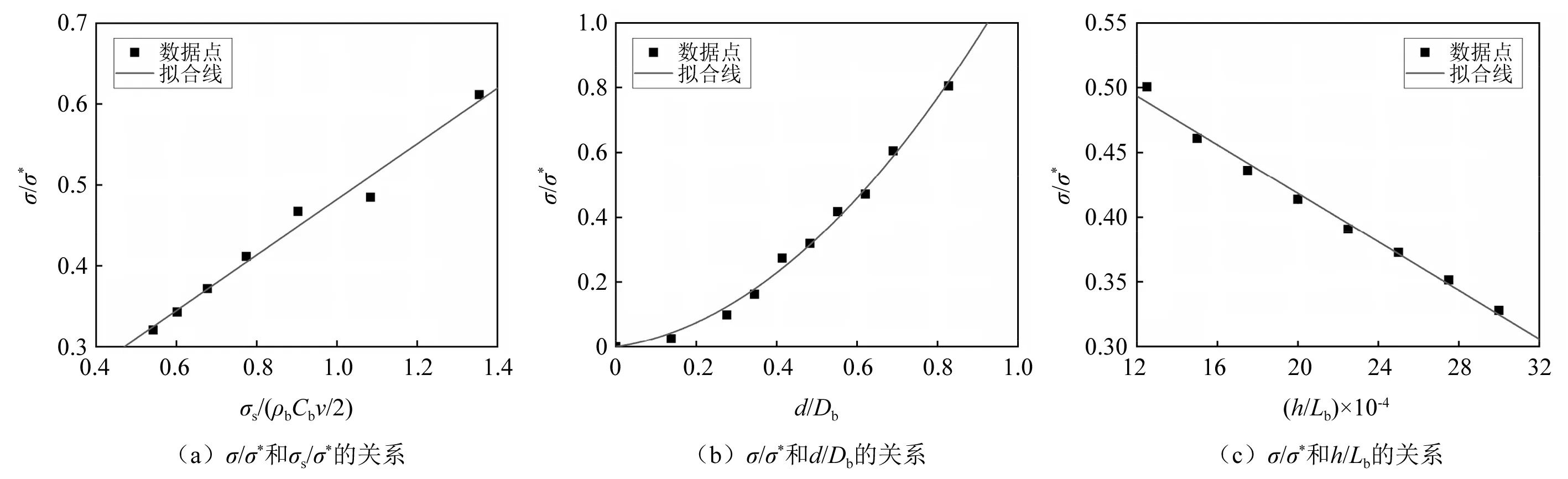
图11 T1拐点无量纲应力与各影响因素的关系
(9)
对于坐标系中的一点,要想确定其准确位置,需要纵坐标和横坐标来共同确定,故得到入射波T1无量纲时间与式(7)右边的三种无量纲参数的对应关系,如图12所示。同样也对此进行了拟合,得到T1拐点的无量纲时间表达式
图12 T1拐点无量纲时间与各影响因素的关系
(10)
4.6 T2拐点的定量分析
对于入射波形T2拐点的确定,由于其理论无量纲应力值为1,故选取T2时即入射波形的震荡部分中点为1时的点为T2点。T2拐点的影响因素主要有整形器的厚度和撞击杆的速度,撞击杆的长度和整形器直径对其的影响可以忽略不计,因此式(7)中的K(d/Db)为常数,而T2拐点的无量纲应力都为1,故只考虑无量纲时间t/t*与影响因素h/Lb和σs/σ*的定量关系。T2拐点无量纲时间与各影响因素的对应关系图,如图13所示。发现无量纲时间与两个影响因素都呈线性关系,同样认为无量纲参数h/Lb与σs/σ*是相互解耦的,并对此过程进行了线性拟合,得到T2拐点的无量纲时间表达式(0 图13 T2拐点无量纲时间与各影响因素的关系 (11) 综上所述,入射波T1拐点的无量纲应力和时间可由下面方程组计算 (12) 入射波T2拐点的无量纲应力和时间的表达式如下 (13) 基于直径为14.5 mm的SHPB装置,利用量纲分析理论对考虑整形器的SHPB试验的相似律问题进行了研究,在此基础上,分析了整形器直径和厚度、撞击杆长度和速度对入射波形的影响规律,根据量纲分析的结果,得到了入射波形两个重要拐点T1和T2的无量纲应力和时间的定量表达式,主要有以下结论: (1)假设SHPB装置的原模型和缩比模型中撞击杆和整形器材料相同且满足物理相似,当撞击杆的速度保持不变时,考虑整形器的SHPB装置满足严格的几何相似律。 (2)使用整形器的SHPB试验可以延长入射波的上升沿时间,T1拐点的无量纲应力σ/σ*随着整形器无量纲直径d/Db的增大而变大,但随着撞击杆速度v和整形器无量纲厚度h/Lb的增大而逐渐减小;T2拐点的无量纲时间与整形器无量纲厚度h/Lb呈正比,与速度呈反比;撞击杆的长度主要影响入射波的持续时间,对入射波的上升沿没有影响。 (3)SHPB试验脉冲整形技术是产生一个与待测试件应力响应(透射波形)相似的入射波形,同时入射波形的T1拐点与反射波平台段的起始点呈正相关,当试验应变率增大时,应增加整形器的直径和撞击杆的速度;T1拐点的无量纲应力σ/σ*和无量纲时间t/t*与影响参数σs/σ*,d/Db和h/Lb分别呈线性、二次函数和线性关系;T2拐点的无量纲应力σ/σ*始终为1,无量纲时间t/t*与σs/σ*无量纲参数h/Lb与σs/σ*都是呈线性关系的。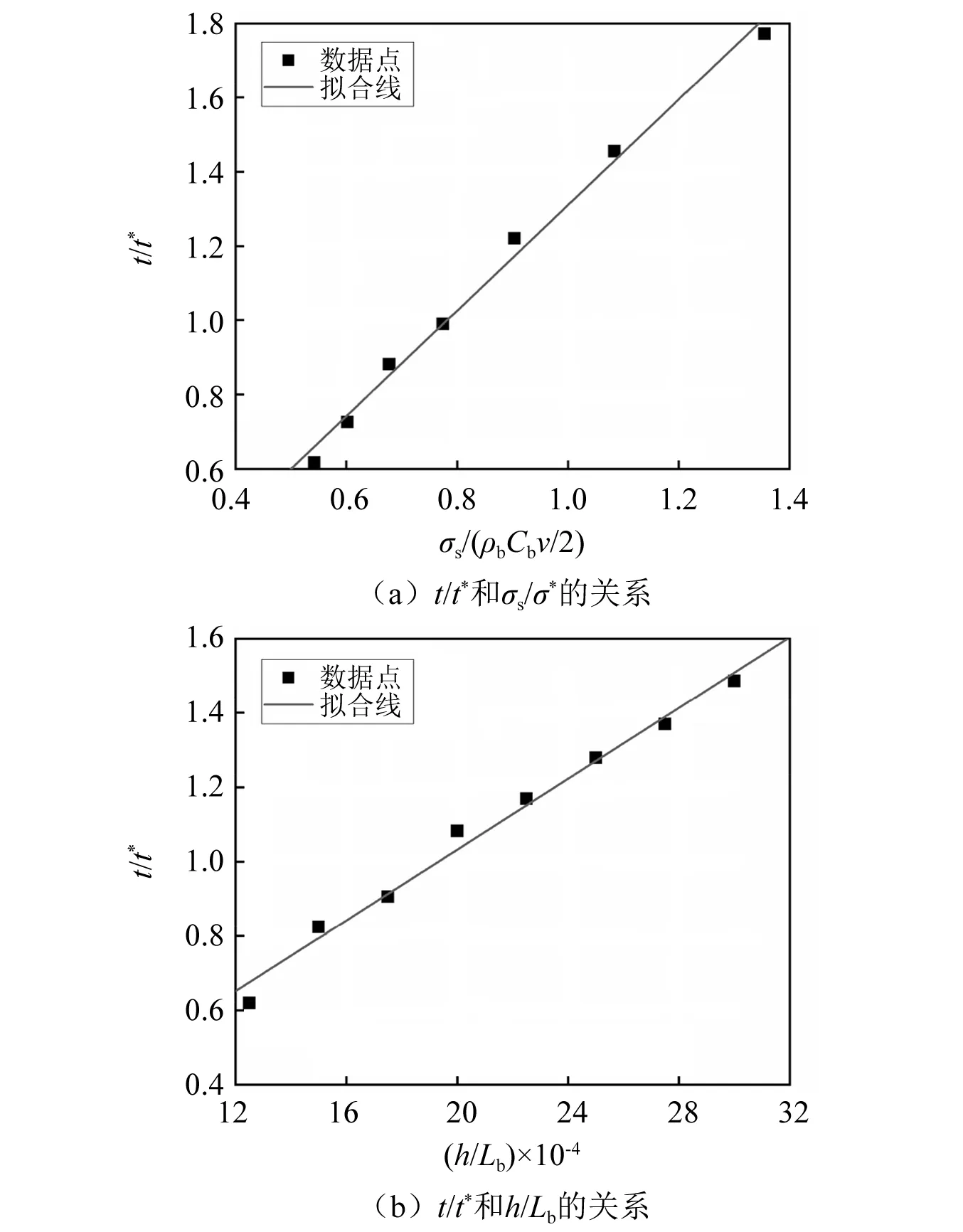
5 结 论
