海洋缆索对水下航行器的动态响应
2019-11-19张大朋章浩燕朱克强
张大朋,白 勇,章浩燕,朱克强
(1.浙江大学 建筑工程学院,杭州 310058;2.宁波大学 海运学院,宁波 315211)
有缆ROV(水下机器人)可以安全有效地到达海洋深水区域进行作业,是开展深海勘探的重要工具。本文结合作者之前的研究成果[1],对缆索三维几何形态模型进行了研究。所用缆索三维动态偏微分方程模型为Albow模型[2],通过对缆索动态偏微分方程在时间和空间上离散化处理,将无法确定缆索单元长度的问题转化为缆索单元可确定问题,并采用有限差分法进行了求解,得到航行器直航状态下缆索的几何形态结果,以及回转状态时缆索的几何形态结果。通过将计算结果与实验值进行对比分析,发现计算结果基本在允许误差范围内,说明建立缆索动态模型对航行器运动状态进行预测是可行的。这种计算模型不但可以避免声纳监测横摇速度及纵荡速度的盲区问题,而且可以较为精确地预测航行器的运动[3]。
1 缆索的三维模型
1.1 三维模型坐标系建立
如图1所示,建立三套坐标系,即地面坐标系(i,j,k),缆索局部坐标系(τ,n,b),航行器运动坐标系(iv,jv,kv)。
航行器的运动坐标系与地面坐标系之间的关系可表示为如下
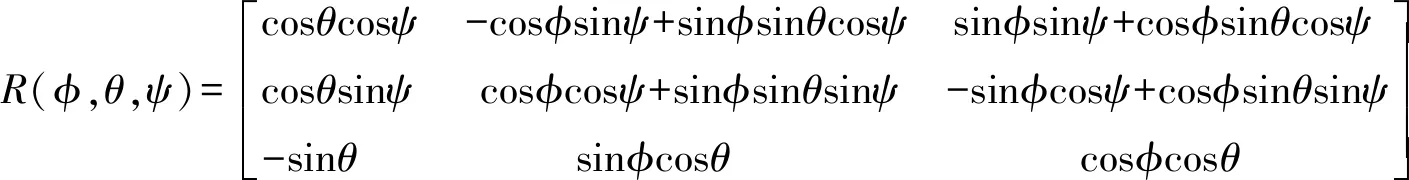
(1)
式中:(φ,θ,ψ)分别为水下航行器的横摇角、纵摇角和艏摇角。
缆索的局部坐标系与地面坐标系之间的关系可以用下式表示
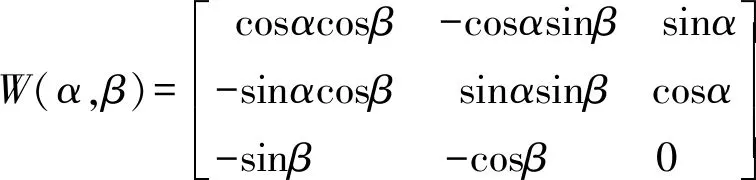
(2)
缆索局部坐标系与航行器运动坐标系之间的关系为
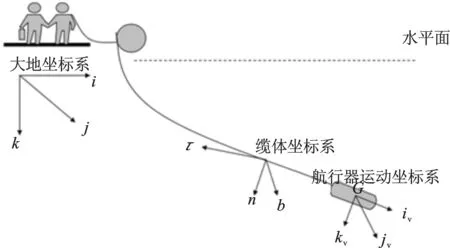
图1 三维模型坐标示意简图Fig.1 The schematic of the three-dimensional model
(3)
式中:(α,β)为如果让整体坐标系与局部坐标系重合,由整体坐标系到缆索局部坐标系需要绕坐标轴旋转的角度。
1.2 缆索三维模型动力方程
y(s,t)=[TVτVnVbαβ]T
(4)
方程(4)代表缆索的几何形态,其中,t表示水下航行器运动时间,s表示弧长,T表示缆索内部张力,Vc=[VτVnVb]T表示缆索某点处的速度向量。因此,缆索的动态方程可以用以下偏微分方程表示
(5)

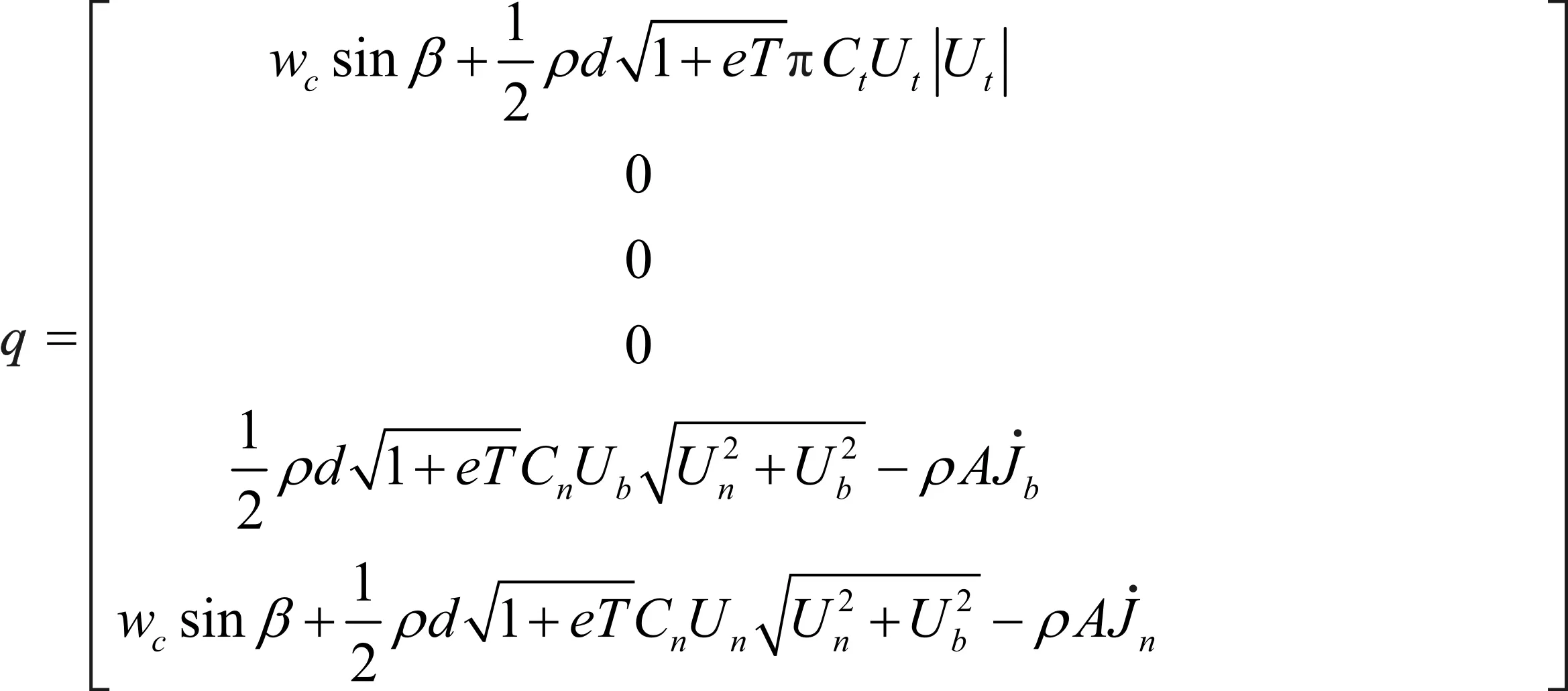
式中:ρ为流体密度,kg/m3;m是单位长度缆索的质量,kg/m;A是缆索未伸长前的横截面积,m2;m1为单位长度缆索实际质量,m1=m+ρA,kg/m;wc为水中缆索单位长度的重量,N/m;e为1/EA;ct为切向拖曳力系数;cn为法向拖曳力系数;d为缆索拉伸后的直径,m;J为局部坐标系下流体的顺势速度,J=[Jτ,Jn,Jb]T,m/s;U为缆索的相对速度,U=[UτUnUb]T,U=Vc-J,m/s。
1.3 缆索三维模型动力方程边界条件
缆索与水下航行器连接端的三个边界条件
Vc(0,t)=WT(α,β)R(φθψ)(V+Ω×rc)
(6)
由于岸上卷筒对缆索的作用力主要是切向力,因此卷筒与缆索连接端运动速度的法线方向和副法线方向的速度分量均为零,因此第四及第五个边界条件如下所示
Vn(St,t)=0Vb(St,t)=0
(7)
卷筒与缆索连接端的第六个边界条件表示为
(8)
1.4 缆索对航行器的作用力
初始时刻,拖点处航行器所受缆索的作用力及力矩为T(0,t),Γf(0,t)。航行器所受缆索作用力,在航行器运动坐标系中可以表示如下
(9)
拖点处航行器受缆索的作用力矩,在航行器动态坐标系中,缆索拖点处由缆索引起的力矩可以表示为
(10)
1.5 缆索三维模型求解过程
求解缆索的动态偏微分方程的数值方法有很多,由于本系统中缆索长度并非定值,而是受到滚筒和航行器的控制,随着航行器的移动,缆索的浸水量在不断变大。本文主要采用有限差分法进行求解,最后通过将计算结果与实验结果及其他算法结果进行对比,来说明有限差分法对求解缆索动态偏微分方程的优势。
首先假设缆索的浸水初始长度为0,Sτ表示τ时刻缆索的长度。缆索的浸水总长的求解方程可以表示如下
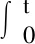
(11)
t=k+1时刻,即将入水的缆索单元的近似动态偏微分方程,下面对缆索偏微分方程进行有限差分求解。
边界条件
Vc(S0,tk+1)=WT(α(S0,tk+1),β(S0,tk+1))R(φ,θ,ψ)(V+Ω×rc)
(12)
Vn(Sk+1,tk+1)=0
(13)
Vb(Sk+1,tk+1)=0
(14)
(15)
总结以上求解过程可知,运用有限差分法通过Matlab求解缆索三维动态方程的步骤总结如下:
(1)设定步长及计算总时间。
(2)设定计算的初始值,本文中初始时刻时,浸水缆索的长度为0,此刻,由于卷筒出缆端还未出缆,因此初始时刻卷筒出缆端与航行器连接端一致。由此,将代入缆索的初始形态即中求解。
(3)设定边界条件,由于本文中所用缆索有两个连接端,即缆索与水下航行器尾端的连接处(拖点),以及缆索与岸上卷筒的连接端。因此,在求边界条件时,两个连接端的边界条件都要考虑。
(4)确定每段缆索元的长度。
2 缆索三维模型案例分析
2.1 直航案例
本案例中所述缆索为轻质等浮力缆索,首端连接在航行器的尾部(作为拖点),拖点在航行器运动坐标系中表示为rc=(-0.5,0,0);尾端与卷筒相连(作为放缆端),卷筒直径约为0.2 m,并假设卷筒放缆端保持松弛状态,即此处缆索张力为零,那么在放缆处,卷筒与缆索的滑动摩擦力产生的力矩为Γf=0。缆索的相关参数及流体的相关参数见表1。

表1 直航案例中缆索与流体参数表Tab.1 Parameters of cable and seawater
航行器前进过程中直航运动
u=1 ,v=w=0,p=q=r=0及θ=φ=ψ=0
(16)
拖点处缆索张力的大小随St变化而变化,进一步分析,可以从浸水缆索总长得到关系式St=t。因此,拖点处缆索张力求解方程式可以近似表示为
(17)
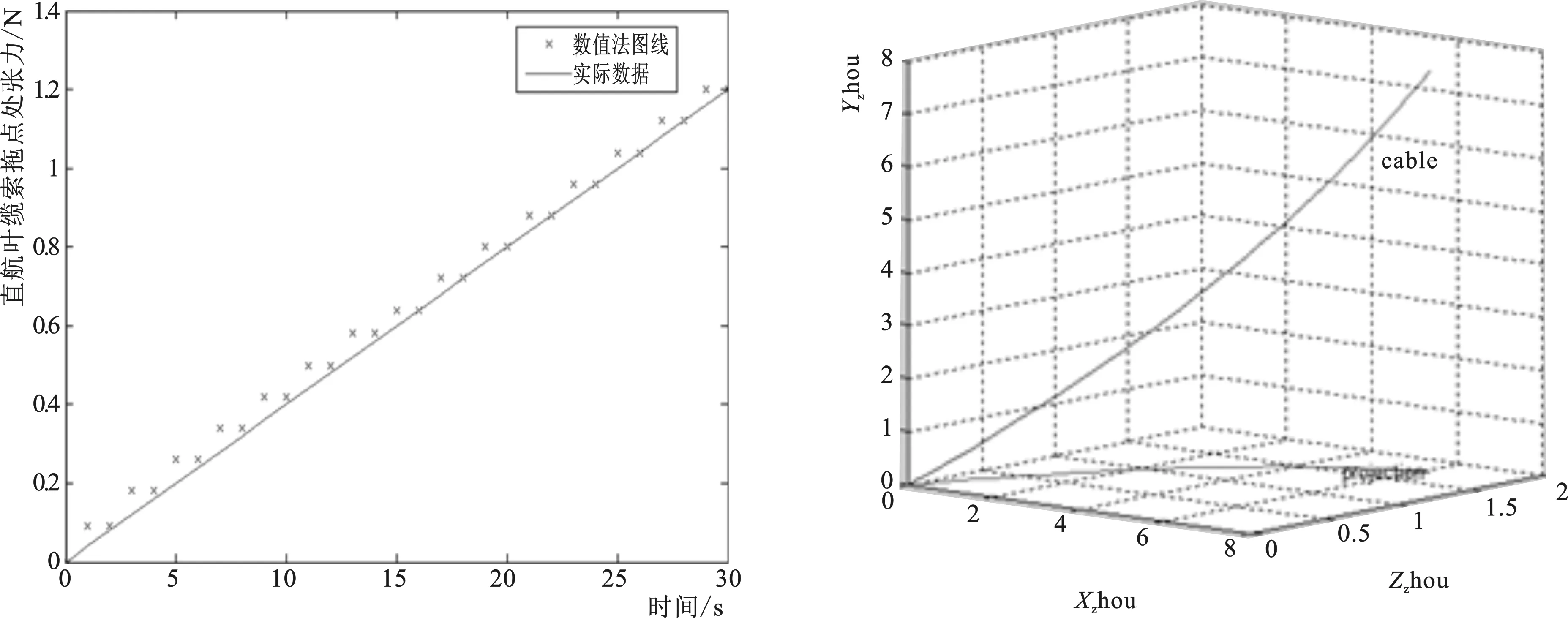

2-a 直航情况下缆索内部张力变化图2-b 直航情况下缆索几何形态图图2 直航时的响应结果Fig.2 The dynamic response of the model during direct sailing
由图2-a可知,在初始时刻,航行器拖点处的缆索张力为0,且张力大小随着航行器运动时间推移呈线性增长趋势。据此可推断,航行器的驱动力在直航过程中,需要不断增大,否则无法保持航行器匀速直航运动状态。从张力的增长方式上看,直航情况下,拖点处缆索的张力随时间推移线性增长,可以据此来求得一段时间内缆索内部最大张力,从而为拖曳过程中航行器直航时间、距离及升沉限制提供依据。同时,在设计有缆ROV系统时,应充分考虑缆索对航行器的动态影响,并根据直航过程中缆索的几何形态来预测航行器的运动状态,从而指导航行器作业。
观察图2-b可知,直航情况下,缆索的几何形态y(Sk+1,tk+1)在X-Y-Z地面坐标系中近乎呈一条直线。这说明,在航行器以某一确定速度直航时,可保证缆索水下构型不发生弯扭及缠绕,而呈现近乎直线的状态。

表2 回转运动参数Tab.2 Parameters of the turning process
2.2 回转案例
为了求得航行器回转运动时,缆索的几何形态。其中,缆索的具体参数、计算时所用时间步长及基本假设与直航情况相同。航行器回转运动时的运动参数如表2所示。

图3 回转运动缆索形态俯视图Fig.3 The configuration of the cable during turning process

数据来源回转运动开始沉深(m)回转运动终点沉深(m)绝对差值(m)最低沉深(m)实验值10.0510.137.452.49有限差分模型11.9711.148.233.21
表3中的实验值是将实验测得的一系列数据求均值得到的。从表3与图3中实验值与模拟值的数据对比可以看出,运用有限差分模型得到的开始沉深、终点沉深及最低沉深与实验值的误差较小,均在有效范围之内。由此可见,建立缆索回转运动模型来预测航行器的运动,是有效的,避免了实时监测过程中对横摇及垂荡速度监测的盲区[4-6]。这里需要指出的是,由于升沉运动的方向使得其在升沉方向的附连水质量较大,这就导致其实验时受到的水的阻尼力较大,因此也就导致了实验值和有限差分模型计算出的最低沉深差别较大,除此之外,水的黏性也是造成沉深的实验值和仿真值有一定差异的一个原因。如果对实验中水流的相关参数进行进一步调整的话,可进一步减小误差。
3 结论
根据计算结果可确定浸水缆索的几何形态[7-14], 这对实际的工程实践有很强的指导意义。仿真结果告诉我们:
(1)在设计有缆ROV系统时,应充分考虑缆索对航行器的动态影响,并根据直航过程中缆索的几何形态来预测航行器的运动状态,从而指导航行器作业。
(2)在航行器以某一确定速度直航时,可保证缆索水下构型不发生弯扭及缠绕,而呈现近乎直线的状态。
(3)由于浸水缆索的长度随着时间推移在不断增长,那么缆索单元的数目也将随着拖曳时间的推移在不断增多,所以无法单纯地将缆索切分为定长度定数目的缆索单元。然而,目前由于有限差分法只能在确定每个缆索单元的长度后才能进行求解,因此,在采用有限差分法时,需要首先确定缆索元的长度。这也是本文的不足,后续将对本研究方法进行进一步优化。
