构建有理函数逼近式的一种新方法*
2016-04-14孙定浩赵长春
孙定浩,赵长春
(1.北京控制工程研究所,北京100190;2.北京圣业科技发展有限公司,北京100190)
构建有理函数逼近式的一种新方法*
孙定浩1,赵长春2
(1.北京控制工程研究所,北京100190;2.北京圣业科技发展有限公司,北京100190)
为超越函数提出一种构建有理函数逼近式的方法.与Pad'e法不同,这种新方法利用超越函数的值与其逼近式的值相互逼近这个条件,较少地依赖超越函数的泰勒展开式.以两个超越函数为例,叙述了用这种方法构建的逼近式与Pad'e逼近式的不同.用这种方法构建了一系列适合在单片机上运行的超越函数的有理函数逼近式.
有理函数逼近式;Pad'e逼近式
0 引 言
实时计算超越函数的值,在机器人﹑实时图像处理和实时语言处理等技术领域均有广泛的应用.硬件实现超越函数计算的算法有查表法﹑基于查表的多项式结合法﹑有理函数逼近法等.可根据允许的最大相对误差﹑允许的计算时间和占用存储空间这3个因素适当选用.
本文讨论有理函数逼近法.文献[1-2]叙述了用Pad'e法构建有理函数逼近式(以下简称“逼近式”)的基本思想.
这表明,对于一个超越函数f(x),首先要把它展开成泰勒级数至“尽可能多的项”,然后才能用这种方法;并知,当要求逼近的最大相对误差愈小,则要求f(x)的泰勒级数展开到愈高的幂次.这一要求,当面临一个较为复杂﹑未知其泰勒展开式时,颇感不便.
更重要的是,Pad'e法[1-2]只注意超越函数f(x)与其逼近式两者泰勒展开式“尽可能多的项”相同,忽视了可以利用f(x)与其逼近式两者的值“相互逼近”这一条件.笔者认为,从实用考虑,在构建逼近式时,可利用这个条件来降低为减少逼近式最大相对误差而要求将f(x)展开到更高幂次的依赖(相对误差的定义:f(x)的真值与逼近式的值的差,与逼近式的值的比值).
本文提出一种构建逼近式的方法:
(1)它只利用超越函数f(x)的f(0)、f(1)(0) (当f(1)(0)=0时则需f(2)(0)),以这些值构建一个给定形式的,但包括了一个或多个待定常数的逼近式(式(3)),称为“一次逼近式”.
(2)再令x在某一点或多点上,f(x)与其逼近式的值相等,以确定这个逼近式中的待定常数.
(3)验算所得逼近式在给定的x区间[0,1]的最大相对误差,若不满足设定的值,则改变前次设定的一点或多点,重复上述过程.当断定不能找到这样的一点或多点,则转移到更高次的逼近式(式(16)或式(27)),重复类似的搜索过程.
我们将本文构造的逼近式分为3个层次,分别称为一次﹑二次﹑三次逼近式,现说明如下.
1 一次逼近式
超越函数f(x)的泰勒级数的一般形式为
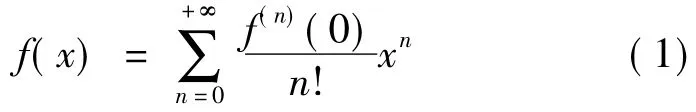
将给定的f(x)的泰勒展开式中实际存在(f(n)(0)≠0)的前四项(其后诸项x幂次的增量均为k)表示成

其中f(0)为常数项,m为f(m)(0)≠0的最低幂次,k为m幂次以后再次出现f(m+k)(0)≠0的x的幂次的增量.将f(0)﹑m﹑f(m)(0)和k作为f(x)的4个特征参数.
用这4个特征参数构建一个新的函数,它由f(0)和x的有理函数式之和组成,用符号表示:

其中A、B为待定常数.
(1)对于基本的对数函数、三角函数和反三角函数,可设A=1.在x区间[0,1]选定一点x0(根据表3(a),这个x0一般在0.7~1之间).按前述方法令
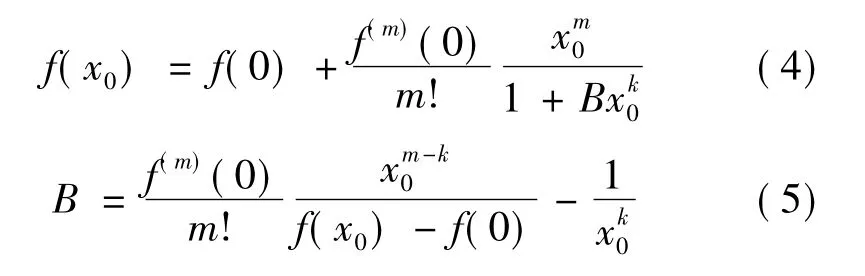
将A、B代入式(3)得.在x的给定区间,以一定步长逐点验算的相对误差.表3(a)的结果表明,可以搜索到一个x0值,使的最大相对误差max|Er|<1%.
(2)对于指数函数ex以及其他用式(5)未能得到max|Er|<1%的函数,可将式(3)中A、B均作为待定常数.选定两点x0,x1(根据表3(a),这个x0,x1一般在0.7~1之间).令

将式(6)、(7)联立求解得A、B值代入式(3)得.按上述相似的搜索法,一般能找到最大相对误差小于1%的逼近式.
例1

得知f(0)=0,m=1,f(1)(0)=1,k=1.将这些值代入式(3)(不包括f(2)(0),f(3)(0))得

搜索得到x0=0.8代入式(5)得B=0.451 3,此时式(9)的最大相对误差小于1%.
用Pad'e法构建f(x)=ln(1+x)的有理函数逼近式(用Rm,k(f(x))表示这类逼近式,其中m是逼近式中分子多项式的幂次,k是分母多项式的幂次)R1,1(ln(1+x)),则需f(0)=0,f(1)(0)=1,f(2)(0)=-1,构成的逼近式为

若用Pad'e法构建R2,1(ln(1+x)),则还需要f(3)(0)=2,构成的逼近式为
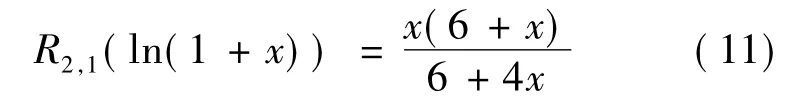
表1示出式(9)~(11)各自的相对误差,用符号Er{…}表示.结果表明,以本文方法所得的逼近式(9)的最大相对误差最小.
例2
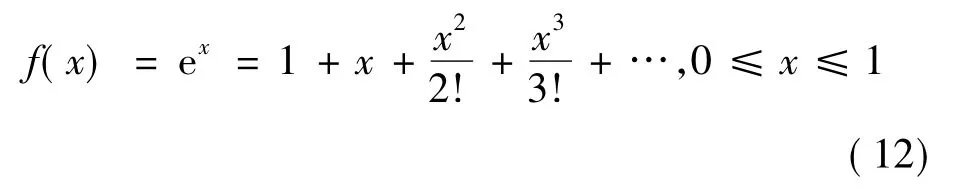
式中,f(0)=1,m=1,f(1)(0)=1,k=1.按式(3)构建的一次逼近式为
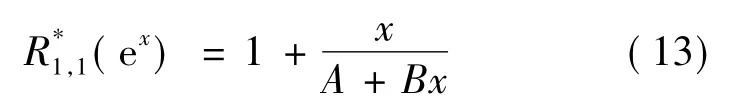
x在区间[0,1],搜索到x0=0.7,x1=0.9,求得A= 0.949 2,B=0.369 5时,式(13)的最大相对误差小于1%.

表1 相对误差(式(9)~(11))Tab.1 Relative errors
若用Pad'e法构造逼近式R1,1(ex),需要f(0)= 1,f(1)(0)=1,f(2)(0)=1.
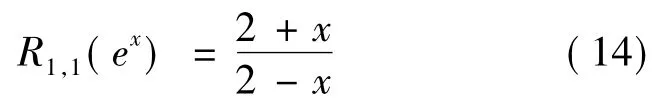
若用Pad'e法构造逼近式R2,1(ex),还需要f(3)(0)=1.

表2示出式(13)~(15)各自的相对误差.结果表明,以本文方法所得的逼近式(13)的最大相对误差最小.

表2 相对误差(式(13)~(15))Tab.2 Relative errors
表3(a)示出本文构建的一系列超越函数f(x)的一次逼近式;表3(b)列出在单片机At89c52(晶振24 MHz)上的执行时间.

表3(a) 一系列适用于单片机的超越函数的一次逼近式,0≤x≤1Tab.3(a) An approximation of transcendental function,0≤x≤1

表3(b) 函数f(x)及其一次逼近式的执行时间Tab.3(b) The execution time forf(x)and its one time approximation
2 二次逼近式

其中A、B、C为待定常数.其构造原则和一次逼近式相同.
令A=1,在x区间选择两点x0、x1,令
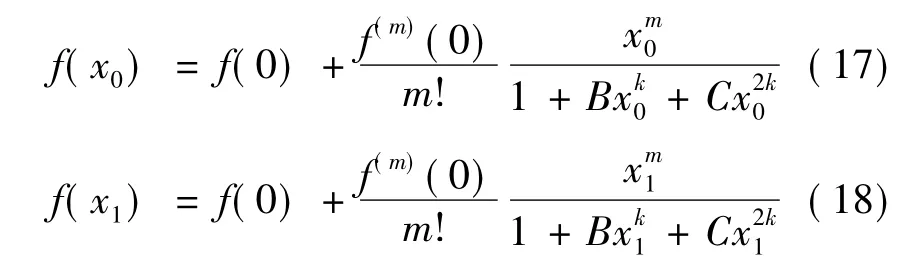
联立求解得出B、C表达式代入式(16)(A=1)得.按上述相同的搜索法,一般能找到最大相对误差约0.1%的逼近式.
当A也作为待定常数,则需选择3点x0、x1、x2,对x2建式(19)

将式(17)、(18)(令其分母中常数1改为A)与式(19)联列,解此3个未知数的线性代数方程组得A、B、C的值.
例3
针对式(8),设A=1,则二次逼近式为
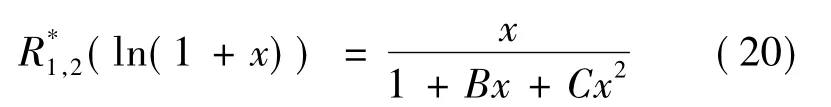
搜索到x0=0.45,x1=1时,得到B=0.490 7,C=-0.049 02,可使逼近式(20)的最大相对误差小于0.1%.
用Pad'e法构建R1,2(ln(1+x)),则需知

用Pad'e法构建R2,2(ln(1+x)),则还需知f(4)(0)= -6.

表4示出式(20)~(22)各自的相对误差,逼近式(20)的最大相对误差最小.
例4
针对式(12),按式(16)(令A=1)得

搜索到x0=0.6,x1=1时,得到B=-0.498 7,C= 0.080 7,可使逼近式(23)的最大相对误差小于0.01%.
用Pad'e法构建R1,2(ex)),则需知f(0)=f(1)(0)=f(2)(0)=f(3)(0)=1.

用 Pad'e 法 构建R2,2(ex),则 还 需 知f(4)(0)=1.
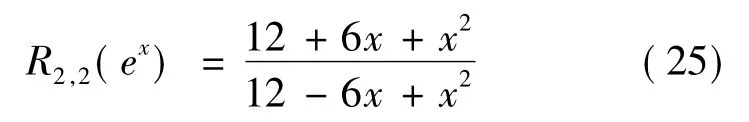
表5示出式(23)~(25)的相对误差.式(23)的最大相对误差最小.

表4 相对误差(式(20)~(22))Tab.4 Relative errors
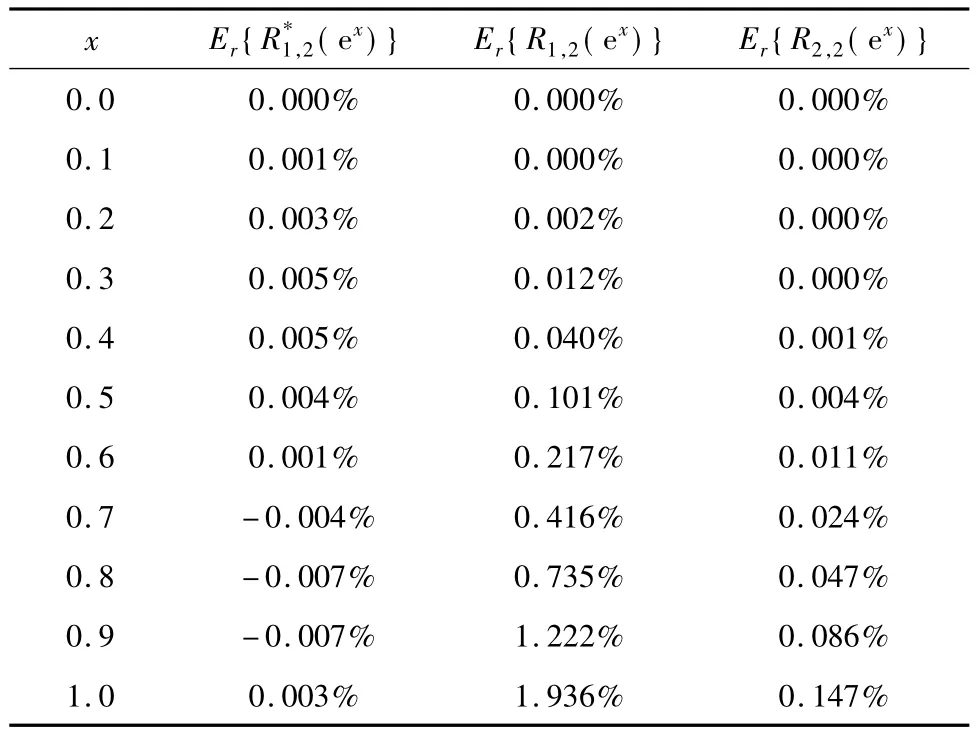
表5 相对误差(式(23)~(25))Tab.5 Relative errors
3 三次逼近式
式(2)可改写成

将式(26)中括号内的幂级数,用式(16)来逼近,得
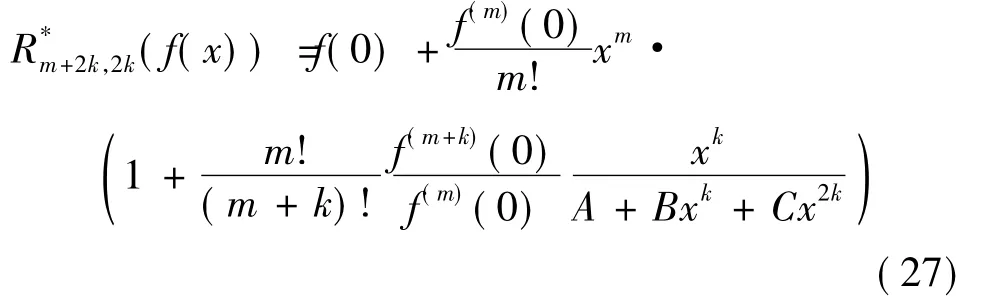
其中A、B、C为待定常数.
令A=1,现作以下推导.
按前述方法,在x区间[0,1]内选择两点x0、x1,令
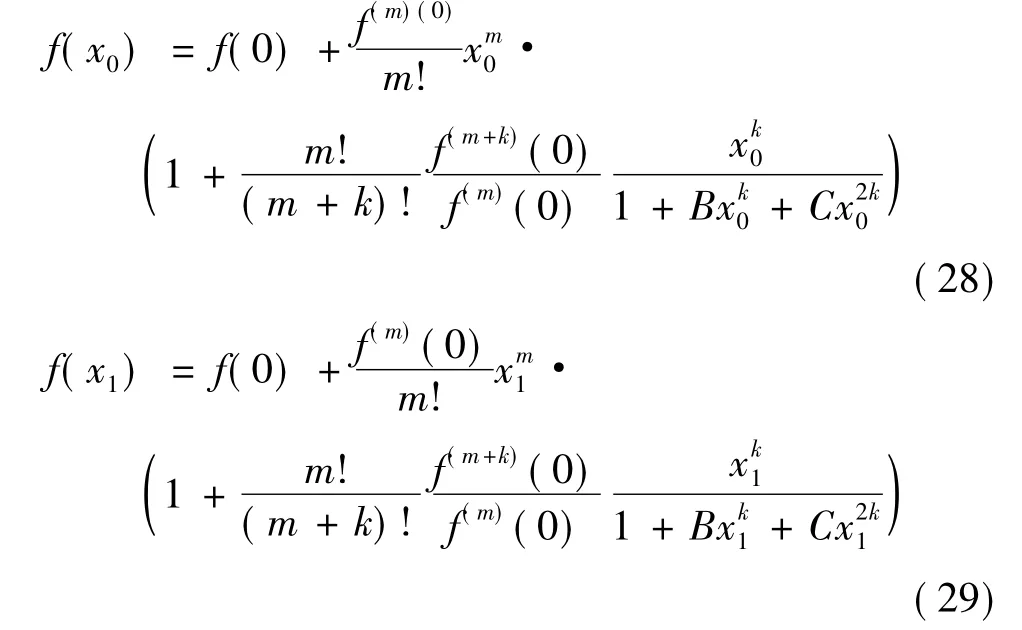
联立求解得出B、C代入式(27)(A=1)得.用上述相同的搜索法,一般能找到最大相对误差约0.01% 的逼近式.
当A也作为待定常数,则搜索3点x0、x1、x2,按前述方法得3个线性方程,解此方程得A、B、C,从而确定三次逼近式.
例5
针对式(8),取f(0)=0,m=1,f(1)(0)=1,k= 1,f(2)(0)=-1,由这些值构建A=1的三次逼近式(27)得

搜索到x0=0.65,x1=1,得到的B=0.658 1,C= 0.028 6,可使式(30)的最大相对误差约0.01%.
用Pad'e法构建R3,2(ln(1+x)),则需知f(0)=0,f(1)(0)=1,… ,f(5)(0)=24.

R3,2(ln(1+x)))的最大相对误差为0.027%.
表6示出式(30)、(31)的相对误差值.式(30)的最大相对误差比式(31)的小.
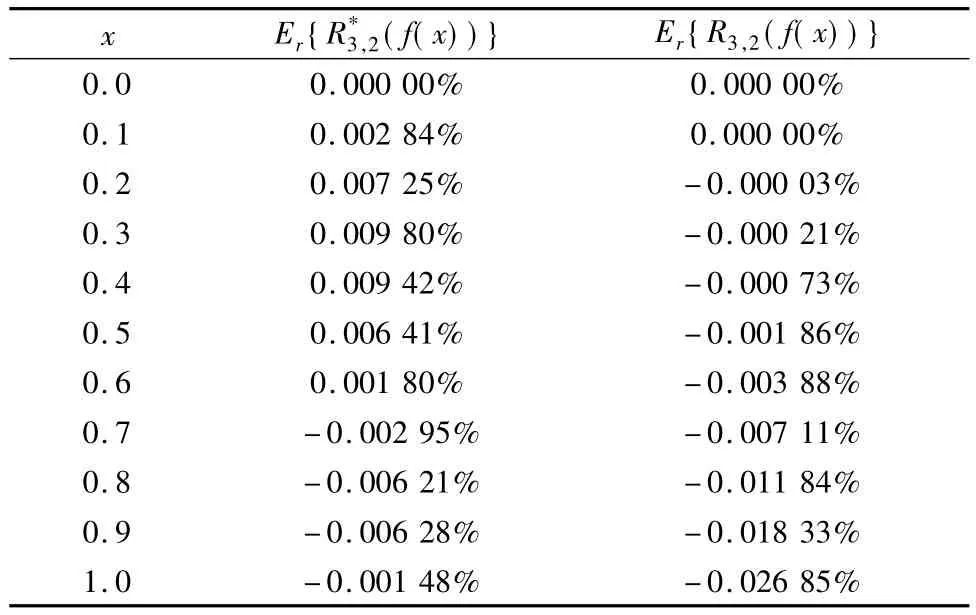
表6 相对误差(式(30)、(31))Tab.6 Relative errors
例6
针对式(12),取f(0)=1,m=1,f(1)(0)=1,k=1,f(2)(0)=1,由这些值构建A=1的三次逼近式得

搜索到x0=0.6,x1=1,B=-0.334 3,C=0.030 4,可使三次逼近式(32)的最大相对误差约0.000 8%.
由文献[1]知用 Pad'e[1]法构建R3,2(ex)和R2,3(ex),需知f(0),f(1)(0),…,f(5)(0)的值.

表7示出(32)~(34)的相对误差.式(32)的最大相对误差最小.
4 复合超越函数举例
文献[3]给出下列复合超越函数的泰勒展开式.
例7

式(35)的f(0)=e,m=2,f(2)(0)=-e,k=2由这些值构建A=1的一次逼近式,

表7 相对误差(式(32)~(34))Tab.7 Relative errors
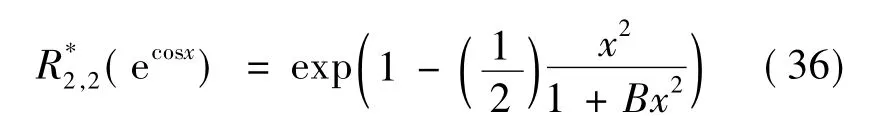
搜索到x=1,得到B=0.356 8,可使式(36)的最大相对误差约0.15%.
用Pad'e法构建R2,2(ecosx)需用到f(0)=e,f(2)(0)= -e,f(4)(0)=4e.

表8示出式(36)、(37)的相对误差.式(36)的最大相对误差比式(37)的小.
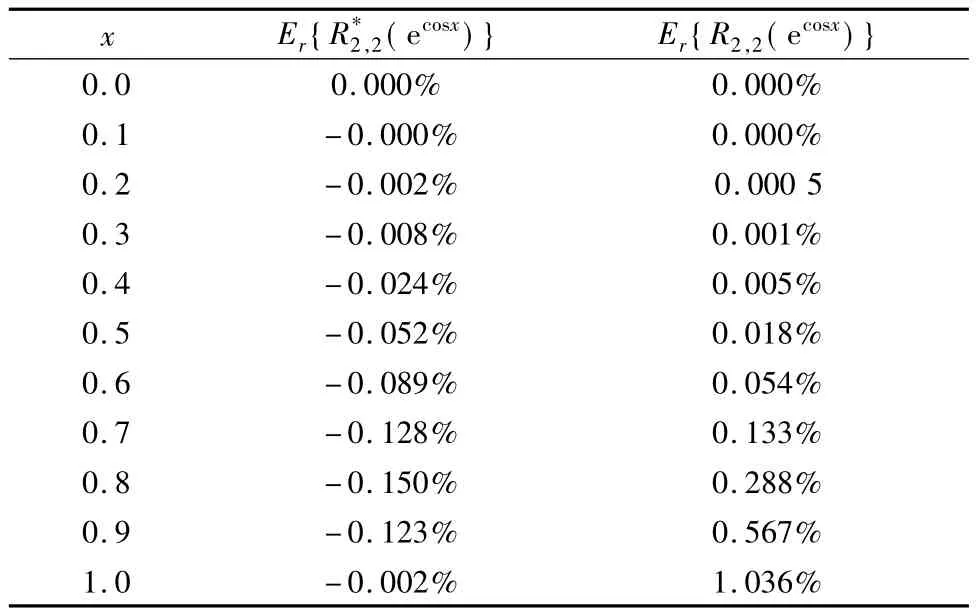
表8 相对误差(式(36)、(37))Tab.8 Relative errors
例8

由式(38)知


对式(39)括号内幂级数用A=1的式(3)逼近,得搜索到x0=1时,由式(5)所得的B=-0.279 3可使式(40)的最大相对误差约0.05%.
用Pad'e法构建R4,2(ln(cosx))得

表9示出式(40)、(41)的相对误差值.式(40)的最大相对误差比式(41)的小.
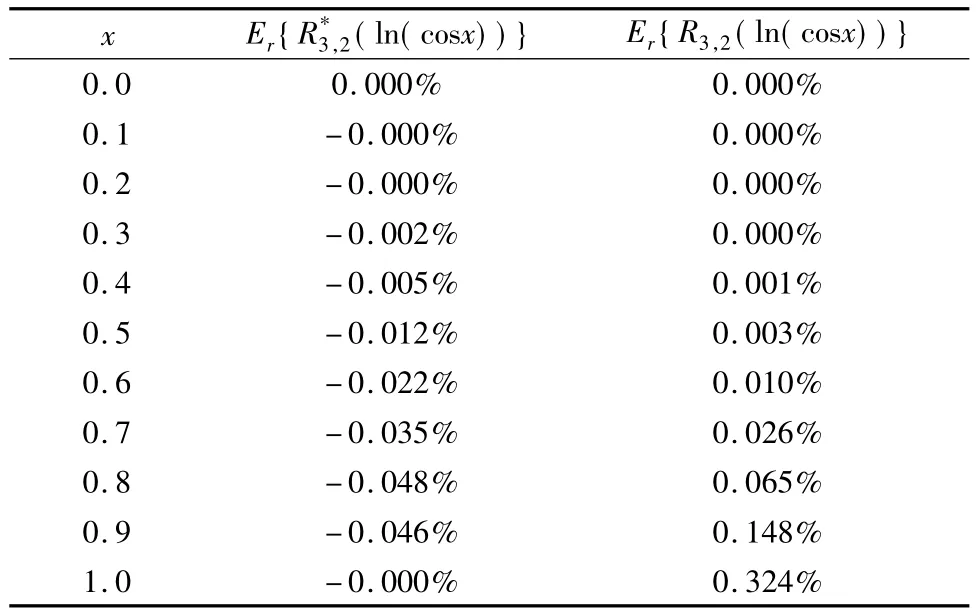
表9 相对误差(式(40)、(41))Tab.9 Relative errors
5 结束语
本文表3及8个举例说明,在构建有理函数逼近式时利用超越函数f(x)与其逼近式的值“相互逼近”这一条件,可减少推导f(x)更高阶的导数,计算其在x=0的值;并使所得的逼近式的最大相对误差更小.
可按不同方式利用“相互逼近”这一条件.本文设x在一点或多点上误差等于零.实际上,也可设误差等于某个值;或以其它方式利用这一条件.
构建有理函数逼近式已有近百年的历史,拥有丰富的内容.笔者谨以此文供读者参考.
[1]徐献瑜,李家楷,徐国良.Pad'e逼近概论[M].上海:上海科学技术出版社,1990:1-30.
[2]切尼E W.逼近论导引[M].徐献瑜,译.上海:上海科学技术出版社,1981:192-230.
[3]《数学手册》编写组.数学手册[M].北京:高等教育出版社,1979:225-231.
A New Kind of Method for Constructing Rational Function Approximations
SUN Dinghao1,ZHAO Changchun2
(1.Beijing Institute of Control Engineering,100190;2.Beijing Shengye Science and Tech.Development Co.Ltd,100190)
A new kind of method for constructing the rational function approximations for transcendental functions is provided.Differing from Pad'e method,the new method utilizes the conditions which the values of the transcendental function and its approximation approximate each other,less depending the Taylor expansion of the transcendental function.Taking both of transcendental functions for examples,the differences between the approximations derived with the method and Pad'e approximations are discussed.Using the method,we construct a series of approximations suitable to operate on microcontroller.
rational function approximation;Pad'e approximation
O174.41
:A
:1674-1579(2016)01-0057-06
10.3969/j.issn.1674-1579.2016.01.011
孙定浩(1934—),男,高级工程师,研究方向为电功率变换技术;赵长春(1976—),男,工程师,研究方向为电功率变换技术.
*十二五民用航天资助项目.
2014-12-20
