基于ESO的可重复使用飞行器积分滑模控制器设计*

刘贺龙，何英姿，2，刘高同，陈上上

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190; 3.北京卫星环境工程研究所，北京100094)

基于ESO的可重复使用飞行器积分滑模控制器设计*

刘贺龙1，何英姿1，2，刘高同3，陈上上1

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190; 3.北京卫星环境工程研究所，北京100094)

考虑参数不确定和外界干扰对姿态控制的影响，开展基于扩张状态观测器(ESO，extended states observer)的可重复使用飞行器姿态控制研究.首先，对飞行器运动模型进行描述，在合理假设条件下，得到面向控制器设计的纵向和横侧向姿态模型;其次，分别针对纵向和横侧向姿态模型设计积分滑模控制器(ISMC，integral sliding mode control);然后，引入ESO对耦合作用、参数不确定及外界干扰进行估计，并在控制器中进行补偿;最后，六自由度仿真结果表明，本研究给出的控制策略能够实现对给定制导指令的稳定跟踪，确保安全再入飞行.

可重复使用飞行器;积分滑模;扩张状态观测器

0 引 言

可重复使用飞行器［1］再入过程具有大空域、大包线的特点，整个再入过程必须严格满足热流、动压及过载约束，同时，外界环境的扰动及飞行器参数变化导致再入过程变的更为复杂，给控制器的设计及再入过程的实现带来极大难度.

在可重复使用飞行器研究中，采用划分内外双环控制策略，Shtessel［2］针对飞行器的再入模式，基于滑模理论对其姿态控制问题进行研究.Tian等［3］考虑飞行器的非线性耦合特性、参数不确定和外界扰动因素等影响，设计了时变高阶滑模并结合虚拟控制输入，在避免控制抖振的同时，实现了高精度跟踪;文献［4］针对可重复使用飞行器姿态控制问题，Tian等采用双环结构，分别设计了内外环控制器和干扰观测器，并通过控制分配获得舵面指令，结合实时轨迹优化策略，实现了制导控制一体化.在ESO的研究中，Shao等［5］考虑有界不确定影响，将TLC和自抗扰控制(ADRC，adaptive disturbance rejection control)结合，分别针对姿态环和姿态角速率环设计ESO并分析估计误差;Song等［6］采用非线性分数阶PID控制器结合ESO的策略设计了兼具良好稳定性、动态性能和鲁棒性的控制器，但是对ESO估计的精度有待进一步分析.ESO并不能对所有信号实现渐近估计，Zheng等［7］从ESO带宽的角度，对估计误差进行了分析;Yang等［8］进一步从微分方程解的角度对ESO的估计精度进行了探讨.采用传统根轨迹设计方法，纵向通道与横侧向通道解耦的控制策略已在X-43飞行器中得到了应用［9］，在飞行环境更加恶劣的再入过程研究中也有涉及［10］.

本文采用纵向通道与横侧向通道分别设计控制器的控制策略，给出形式简洁且不失控制精度与鲁棒性的控制器.首先，对可重复使用飞行器再入姿态模型进行面向控制建模;其次，根据给定的制导指令，分别针对纵向模型和横侧向模型设计滑模面，并据此滑模面，分别得到纵向和横侧向通道的控制律，采用ESO对系统的“总不确定”进行估计，并在控制律中进行补偿，以降低控制器设计的保守性，减小边界层厚度，提高跟踪精度;最终，以可重复使用飞行器X-33为被控对象，在Matlab中搭建仿真平台，六自由度仿真结果表明，本文提出的控制算法实现了对给定制导指令的高精度跟踪，对外界扰动具有良好的抑制作用.最后，给出本文结论.

1 预备知识和问题描述

一般单输入单输出系统可表示为:

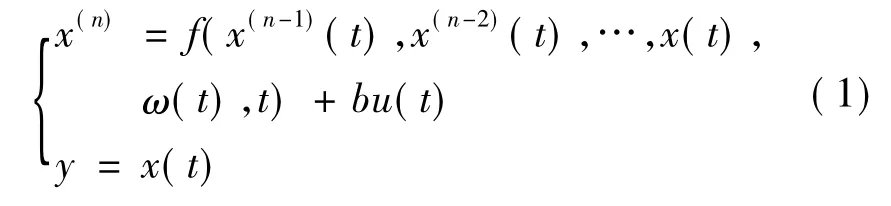
其中，n为系统阶数，y为输出，u为输入，b为常数，ω(t)为外部扰动，f(·)为不确定或系统干扰.

1.1 积分滑模控制(ISMC)及其性质

对系统(1)，易知系统相对阶为n.设输出量为存在.定义误差变量e=y－yr，基于误差变量，积分滑模面定义为

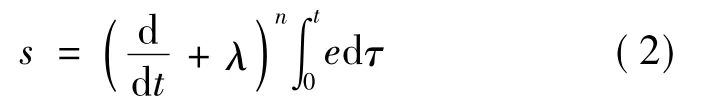
其中，λ为正的常数.为抑制抖振，往往引入边界层，用饱和函数替代符号函数，此时跟踪误差是最终有界且与边界层厚度成正比;积分滑模在滑模面的设计中引入了误差变量的积分，能够减小跟踪误差，获得更高的控制精度.同时，类似于PID算法中积分项的作用，过大的积分作用导致暂态过程较差，需合理选择参数.

1.2 扩张状态观测器(ESO)及其性质

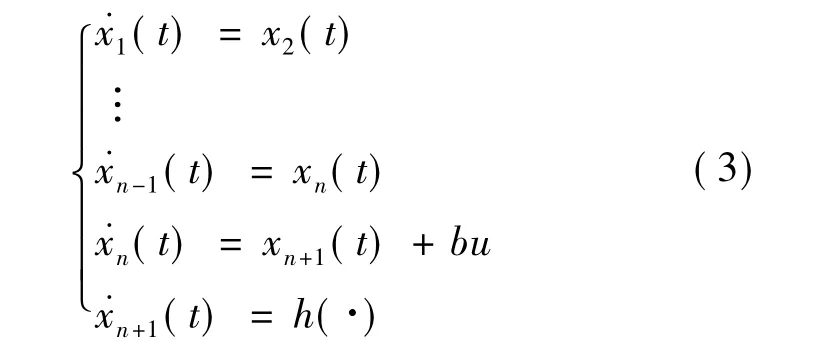
用于估计不确定系统(1)的状态和扩张状态的扩张状态观测器给出如下:

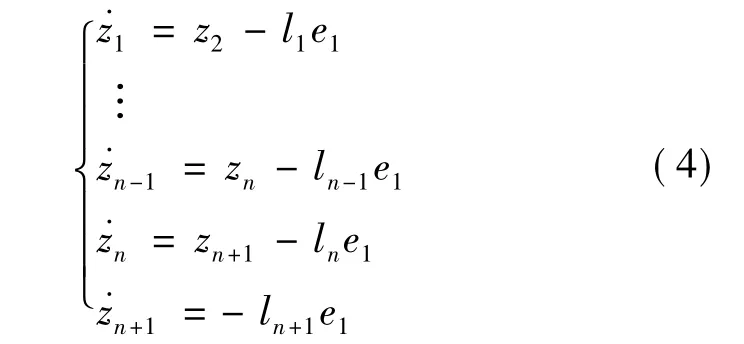
其中，e1=z1－y，li(i=1，2，…，n+1)为观测器的增益，选择合适的增益，即有zi→xi(i=1，2，…，n+ 1).Zheng等［7］指出，若ESO的增益选择为pn+1+l1pn+…ln+1=(p+ω0)n+1的特定形式，ω0为观测器带宽，则ESO的观测误差有界;Yang等［8］又进一步证明，ESO对常值不确定及扰动的观测误差能够渐近收敛到零;对正弦不确定及扰动，ESO观测误差的界与信号带宽幅值及观测器增益相关;对斜坡形式的不确定及扰动，ESO观测误差为常值，与信号变化率正相关.

1.3 问题描述

再入过程是一个复杂的过程，可重复使用飞行器六自由度模型由描述轨迹运动的平动运动方程(5)～(10)和描述姿态运动的转动运动方程(11)～(16)构成［1，4］，其中可执行的制导指令由平动运动方程求解获得，转动运动方程用来进行控制器设计，实现对给定的制导指令的稳定跟踪.

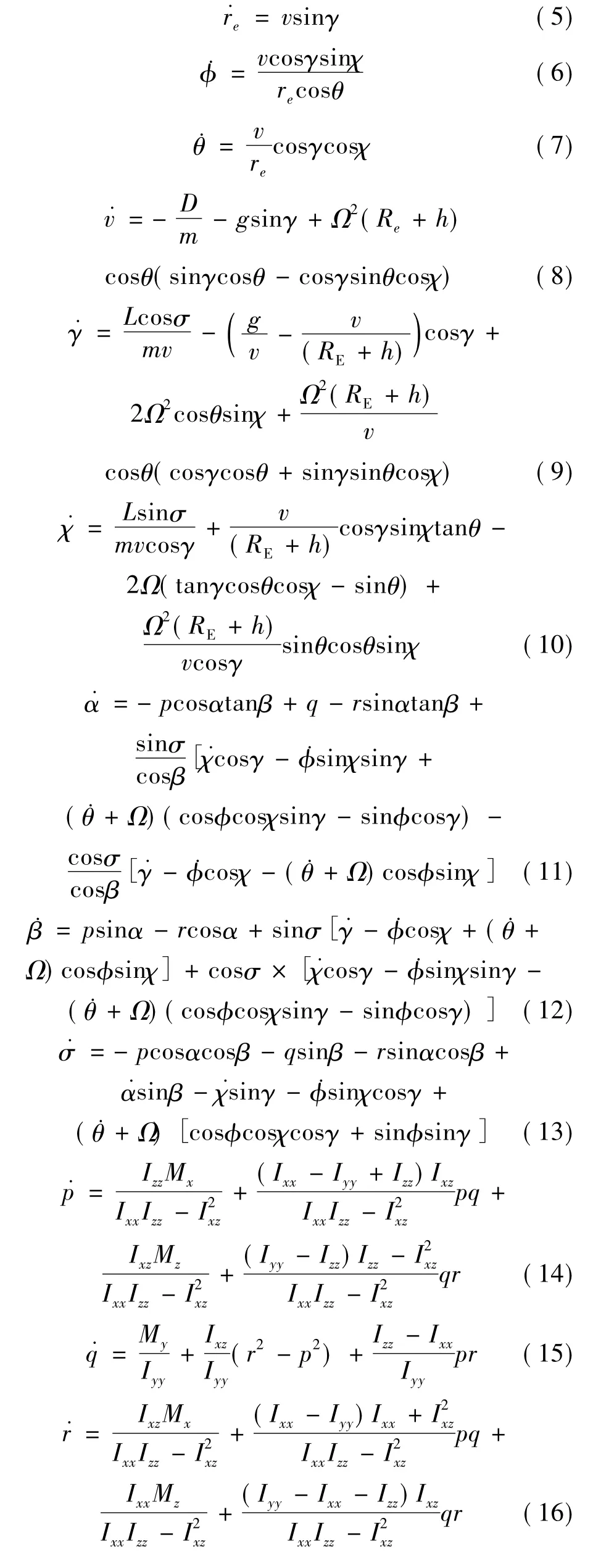
其中:re，φ，θ，v，χ，γ分别表示地心距、经度、纬度、速度、航向角和航迹角;α，β，σ表示攻角、侧滑角和侧倾角;p，q，r分别表示滚转角速率、俯仰角速率和偏航角速率;m表示飞行器质量;Iij(i=x，y，z，j=x，y，z)表示转动惯量;表示引力加速度;μ表示地球引力常量;Ω为地球自转角速度;L和D分别表示升力和阻力，表达式略.

给定该参考信号分别为αref、βref、σref，定义飞行器姿态角的偏差分别为eα=α－αref，eβ=β－βref和eσ=σ－σref.控制目标为:

2 控制器设计

2.1 面向控制建模

实际飞行过程中，地球的自转角速率要远小于飞行器动态，不妨令Ω=0;根据飞行器的动力学及运动学特性可知，飞行器的姿态变量是短周期变量，轨迹变量是长周期变量，在姿态运动方程(11)～ (16)中，可以认为，;再入过程中，一般要求飞行器的侧滑角保持在零值附近，故β=0;针对X-33飞行器面对称的特点，设Iij=0，(i≠j);再入过程中，飞行器受到转动惯量参数不确定ΔIii和干扰力矩ΔMi的影响，转动惯量和控制力矩表达式分别为Iii=Iii0+ΔIii和Mi=Mi0+ΔMi，i=x，y，z，Iii0表示转动惯量标称值，Mi0为待设计控制力矩.飞行过程中，飞行器性能高度依赖于攻角［9］，为此，首先将横侧向动态对纵向的影响忽略，在参数不确定和外界干扰存在的条件下，经过简化得到面向控制器设计的纵向动力学方程:

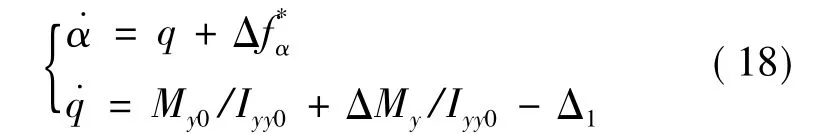
面向控制器设计的横侧向动力学方程:

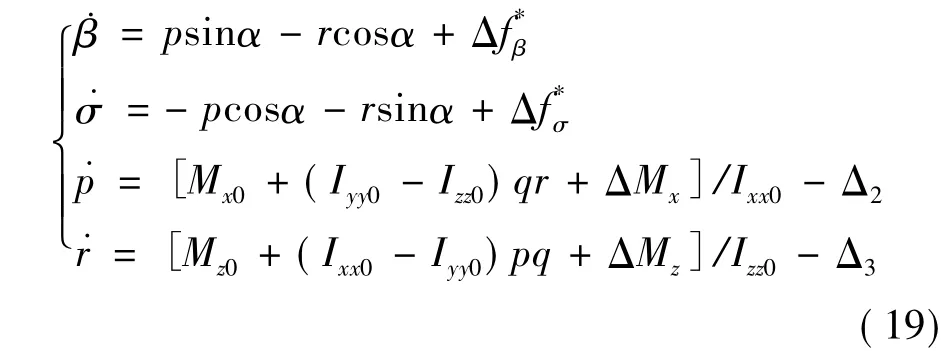
2.2 积分滑模控制器及ESO设计

根据输入输出线性化理论，以姿态角为输出，以控制力矩为输入，相对阶rα=rβ=rσ=2.

对纵向通道，给出如下积分型滑模面:

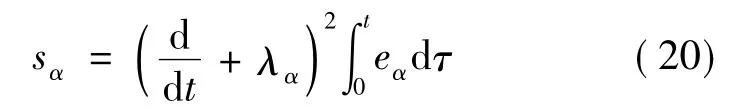
对式(20)求一次导数得:

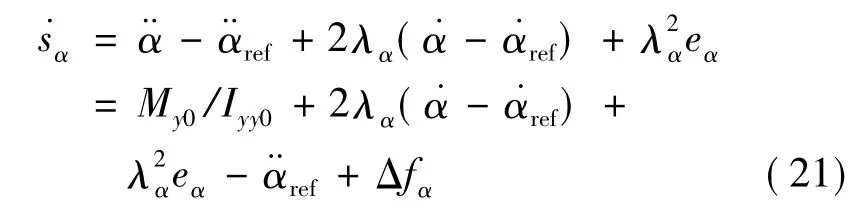
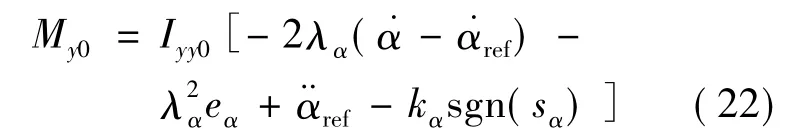
kα是正的常数，当选择增益kα足够大时，在控制律(22)的作用下，使得如下滑动条件成立:

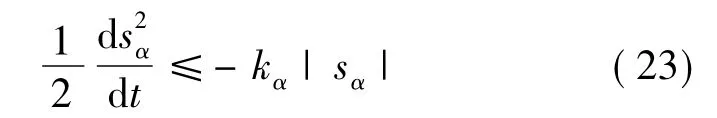
根据横侧向通道的侧滑角偏差和侧倾角偏差，给出如下积分型滑模面:

分别对滑模面(24)、(25)求一次导数得

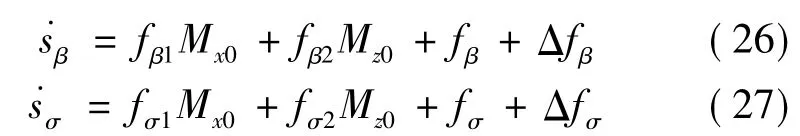
其中，λβ，λσ是正的常数.各符号表达式为:

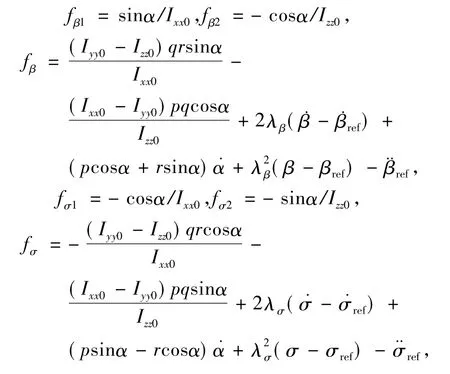
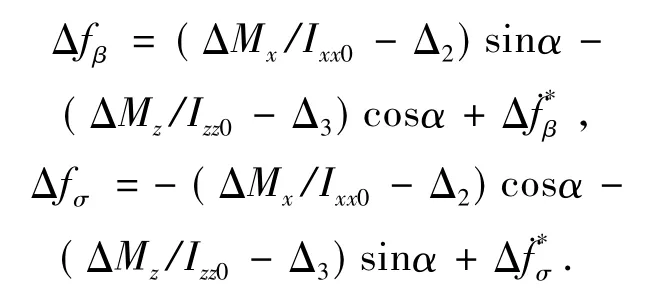
Δfβ，Δfσ表示不确定，且，κβ和κσ均为正的常数.选择横侧向通道控制律:

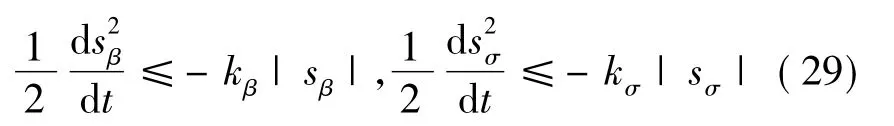
再入过程中，飞行器的姿态运动会受到外界扰动及参数不确定影响，同时，在上述采用分通道策略设计积分滑模控制器的过程中，简化过程额外引入了不确定项.控制器设计过程中，单一依靠滑模控制抑制不确定因素及外界扰动，会导致严重的抖振现象;若以饱和函数来代替符号函数，大的不确定会导致边界层增大，进而导致跟踪误差变大.若不对以上因素的影响进行抑制，会严重影响飞行器的再入过程，甚至导致控制失效.

系统(21)、(26)、(27)可改写为如下形式:

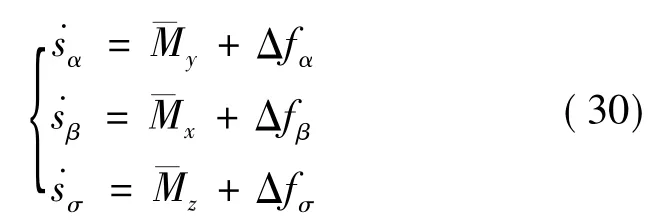
对系统(21)、(26)、(27)，有如下表达式:

那么，针对不确定系统(31)状态和不确定的观测器形式为:

通过选择合适的观测器增益lj1和lj2，就能够很好的估计出作用于系统(31)的不确定影响，且zj2→hj，故zj2→Δfj.

基于扩张状态观测器对系统(21)，(26)，(27)中不确定的估计，再入飞行器纵向通道的控制律如下所示:

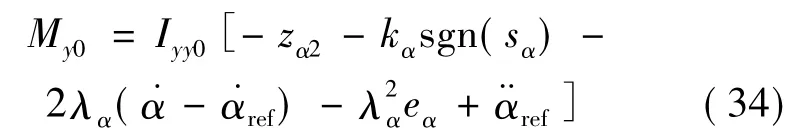
横侧向通道的控制律为:

在不影响系统稳定性的前提下，为避免控制抖振现象，将控制律中的符号函数替换为饱和函数sat(sj/ηj)，其中，ηj代表边界层厚度，是正的常数.

3 仿真分析

3.1 仿真参数设置

在仿真研究中，为更好的验证本文所提出控制策略的有效性，基于文献［11］的工作设计再入制导指令及再入制导律，进行可重复使用飞行器再入段六自由度仿真.初始再入姿态 α0=12.6°，β0=－11.4°，σ0=－28.6°，初始再入姿态角速率p0=q0=r0=0，仿真过程中，参数不确定为 ΔIxx= 0.1Ixx0，ΔIyy=0.1Iyy0，ΔIzz=0.1Izz0;干扰力矩表达式如下:

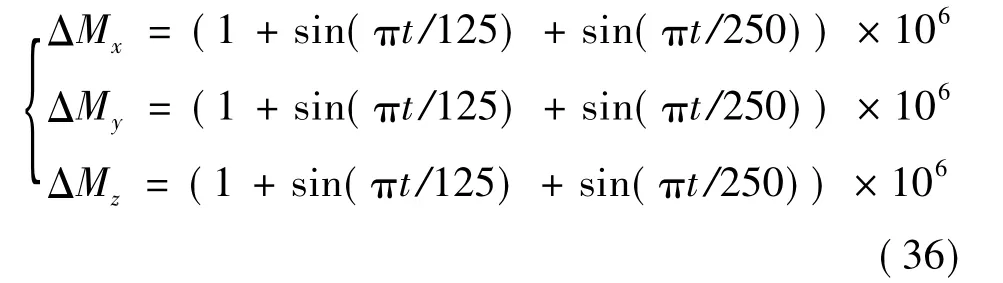
控制器及扩张状态观测器参数设定如下:

不引入扩张状态观测器时，kα=1.5，kβ=1.5，kσ=1.5，ηα=0.1，ηβ=0.1，ησ=0.1.

引入扩张状态观测器时，kα=1.5，kβ=1.5，kσ=1.5，ηα=0.005，ηβ=0.005，ησ=0.005;lα1=lβ1=lσ1=2.5，lα2=lβ2=lσ2=4.

3.2 仿真结果分析

利用本文提出的控制策略，通过六自由度再入仿真，结果如图1～4所示.其中，图1～2为不加ESO的仿真情况，由图1结果可以看出，本文所提出的纵向通道与横侧向通道分别进行控制器设计的策略，能够较好地跟踪姿态角指令，实现飞行器再入.控制器能够在较快时间实现对制导指令的跟踪;图2表明，由于系统不确定及通道间耦合的影响，需要增大饱和函数的边界层，引起一定的跟踪误差，ISMC对制导指令的跟踪效果较为一般.

引入ESO后，飞行器姿态角跟踪曲线如图3所示.从图3可以看出，结合ESO的ISMC很好地实现了对给定制导指令的跟踪，图4表明，引入ESO后，各姿态角的跟踪精度都有了较大程度的提升:攻角跟踪误差|eα|≤2×10－6(°)，侧滑角跟踪误差|eβ|≤7×10－5(°)，侧倾角误差|eσ|≤2.8×10－4(°)，这比ISMC的控制精度提高了至少3个数量级.ESO提升了控制器的性能，基于ESO的ISMC应用于可重复使用飞行器再入过程具有优异的控制精度及鲁棒性.

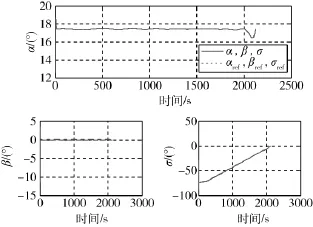
图1 不加ESO的姿态跟踪曲线Fig.1 Attitude tracking curves without ESO

图2 不引入ESO的姿态跟踪误差Fig.2 Attitude tracking errors without ESO

图3 引入ESO的制导姿态跟踪曲线Fig.3 Attitude tracking curves with ESO

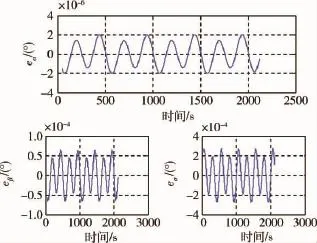
图4 引入ESO的姿态跟踪误差Fig.4 Attitude tracking errors with ESO

4 结 论

本文考虑参数不确定和外界未知扰动对可重复使用飞行器再入姿态控制的影响，采用积分滑模滑模方法(ISMC)和扩张状态观测器(ESO)技术，开展通道解耦的再入姿态控制研究.本文首先分析了再入模型并进行简化处理，得到面向控制器设计的动力学模型，在此基础上设计积分滑模控制器;然后，为估计并补偿耦合影响、参数不确定及外界扰动，对不确定系统进行增广并设计扩张状态观测器.最后，对再入飞行器六自由度模型的仿真结果表明，本研究提出的控制策略很好实现了对给定制导指令的稳定跟踪，完成了再入飞行任务.

［1］田栢苓.高超声速飞行器再入轨迹设计与制导控制方法研究［D］.天津大学.2011.

［2］SHTESSEL Y，HALL C，JACKSON M.Reusable launch vehicle control in multiple-time-scale sliding modes［J］.Journal of Guidance Control and Dynamics，2000，23(6):1013-1020.

［3］TIAN B，FAN W，ZONG Q，et al.Nonlinear robust control for reusable launch vehicles in reentry phase based on time-varying high order sliding mode［J］.Journal of The Franklin Institute，2013，350(7):1787-1807.

［4］TIAN B，FAN W，ZONG Q.Integrated guidance and control for reusable launch vehicle in reentry phase［J］.Nonlinear Dynamics，2015，80(1-2):397-412.

［5］SHAO X L，WANG H L.Active disturbance rejection based trajectory linearization control for hypersonsic reentry vehicle with bounded uncertainties［J］.ISA Transaction，2015，54:27-38.

［6］SONG J，WANG L，CAI G，et al.Nonlinear fractional order proportion-integral-derivative active disturbance rejection control method design for hypersonic vehicle attitude control［J］.Acta Astronautica，2015，111:160-169.

［7］ZHENG Q，GAO L Q，GAO Z Q.On stability analysis of active disturbance rejection control for nonlinear timevaring plant with unknown dynamics［C］//Proceedings of the 46thIEEE Conference on Decision and Control.New York:IEEE，2007:3501-3506.

［8］YANG X X，HUANG Y.Capabilities of extended states observer for estimating uncertainties［C］//American Control Conference.Hyatt Regency Riverfront，2009: 3700-3705.

［9］BAHM C，BAUMANN E，MARTIN J，et al.The X-43A hyper-X mach 7 flight 2 guidance，navigation and control overview and flight test results［C］//AIAA/CIRA 13thInternational Space Planes and Hypersonics Systems and Technologies.Washington D.C:AIAA，2005:1-23.

［10］JEE G，SHARMA K K，RAO K K，et al.Evolution of attitude control law of an Indian reentry launch vehicle［J］.International Journal of Advances in Engineering Sciences and Applied Mathematics，2014，6(3-4): 148-157.

［11］TIAN B，ZONG Q.Optimal guidance for reentry vehicles based on indirect Legendre pseudospectral method［J］.Acta Astronautica，2011，68(6):1176-1184.

ESO-Based Integral Sliding Mode Control Design for Reusable Launch Vehicle

LIU Helong1，HE Yingzi1，2，LIU Gaotong3，CHEN Shangshang1
(1.Beijing Institute of Control Engineering，Beijing 100190，China;2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China;3.Beijing Institute of Spacecraft Environment Engineering，Beijing 100094，China)

Considering the effects of parametric uncertainties and external disturbances on reentry phase，an attitude controller for reusable launch vehicle(RLV)is developed.Firstly，the dynamic model is described.Longitudinal and lateral attitude dynamic models are obtained for controller design under some proper assumptions.Secondly，integral sliding mode controllers(ISMCs)are designed for both of longitudinal and lateral model.Thirdly，coupling effects，parametric uncertainties and external disturbances are estimated by introducing the extended states observer(ESO)，which can be compensated in the controller.At last，numerical simulation for the six degree of freedom reusable launch vehicle is conducted.Results demonstrate that the proposed controller can track the guidance command steadily and accurately，which guarantee a safe reentry flight.

reusable launch vehicle;integral sliding mode;extended state observer

TP273

:A

:1674-1579(2016)01-0031-06

10.3969/j.issn.1674-1579.2016.01.006

刘贺龙(1988—)，男，博士生，研究方向为飞行器控制和空间操作;何英姿(1970—)，女，研究员，研究方向为控制理论与控制工程;刘高同(1986—)，男，工程师，研究方向为空间环境模拟技术;陈上上(1982—)，男，博士生，研究方向为飞行器控制.

*国家自然科学基金资助项目(61403030).

2015-08-15