一类不确定快时变系统的确保性能鲁棒自适应控制*

李公军

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

一类不确定快时变系统的确保性能鲁棒自适应控制*

李公军1，2

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

本文研究了一类一阶不确定快时变系统的确保跟踪性能控制问题.通过引入一个状态变换，将带性能约束的控制问题转化为无约束问题，提出一个鲁棒自适应控制律.该控制律除能确保原系统满足给定的性能约束外，还使得新的状态变量的最终界只和某些控制器参数有关.由于控制器参数已知，因此本方法对该最终界有较好的估计.数值仿真验证了该方法的有效性.

时变系统;快时变参数;鲁棒自适应控制;外部干扰;确保性能控制

0 引 言

当被控对象处于复杂多变的环境中，系统的不确定参数不再是定常或者慢时变的.例如，大型充液航天器在远地点点火阶段，随着推进剂的大量消耗，系统的特性发生较大的变化，此时，系统的某些参数是未知且时变的［1］;高超声速飞行器在下压段飞行时，短时间内动压的变化可达数百倍［2］，是一个典型的快变不确定系统.因此，研究不确定快时变系统的控制问题变得很有实际意义.

关于不确定快变系统的研究，鲁棒控制是常用的方法［3］.鲁棒控制需要知道不确定的界，它可以确保对这个界内的所有不确定都有期望的性能.近年来，针对快变不确定系统，一些自适应控制方法［4-7］也陆续被提出.其中，文献［4-6］要求时变参数及其变化率有界;文献［7］针对一类参数任意快变系统(指:时变参数变化率的上界无法事先限定)，利用浸入与不变流形(I＆I)的设计方法，设计控制器使得在参数估计值有界的条件下，闭环系统状态全局收敛到零.由于自适应控制方法是利用输入输出数据辨识系统的不确定参数，当存在较大干扰时，干扰的存在会极大地影响参数辨识的准确性，导致系统性能变差甚至不稳定.因此，文献［4-7］很难推广到存在有界干扰的情况.

对于那些存在有界外部干扰且控制增益快时变的系统，如果不确定的界未知时，研究成果很少.此时需要将鲁棒控制与自适应控制的思想结合起来，其中自适应控制用来估计不确定的界.在这方面，文献［8］提出了一个确保跟踪性能的鲁棒自适应控制器.该方法通过选取合适的状态变换，使得只要新的状态变量有界，即可实现确保跟踪性能的控制目标［9-11］.然而，仅仅确保新的状态变量有界是不够的，应该尽可能确保所引入的新的状态变量具有较好的性质，例如渐近稳定性或者最终界充分小.这是因为尽管从原系统来看，跟踪性能约束得到满足，但从新的状态变量所描述的系统来看，如果控制器仅仅保证新的状态变量以及其它所有信号有界，系统内部仍然没有达到满意的性能.例如，文献［8］的方法只是确保了新的状态变量以及其它所有信号是一致最终有界的，而且，最终的界正比于高频增益的下界.由于高频增益的下界未知，这个最终界也是未知的，因此不能有好的估计.因此，文献［8］的结果仍然很保守.

基于上述分析，本文考虑一类一阶不确定系统的确保跟踪性能控制问题，其中，时变参数(包括控制增益)和外部干扰只需要是有界的，不需要知道它们的界，因此它们可以是快变的.受文献［8］启发，本文也引入了一个坐标变换，将带性能约束的控制问题转化为无约束控制问题.在此基础上，本文提出了一个鲁棒自适应控制律.该控制律不仅确保原系统具有期望的性能，还能使新的状态变量所描述的系统具有良好的性能.具体地，对于新的状态变量所描述的系统，该控制律不仅确保系统所有信号都是有界的，而且新的状态变量的最终界只和某个控制器参数有关，与系统的参数无关.由于控制器参数都是已知的，本文的方法可以较好地估计这个界的大小.此外，通过适当选取控制器参数，还可以使新状态变量的最终界具有期望的性能.

1 问题描述和预备知识

1.1 问题描述

本文考虑如下一阶快时变系统

其中，x∈R，u∈R，y∈R分别为状态，输入和输出，t为时间，θ(t)为不确定的时变参数，f(t，θ(t)，x)和g(t，θ(t)，x)为未知光滑函数.

对系统(1)，作如下假设:

假设1.函数f(t，θ(t)，x)满足

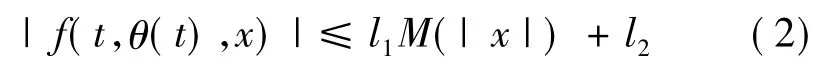
其中M(x)为已知光滑函数，满足M(|x|)≥0，l1和l2为未知正常数.

假设2.控制增益g(t，θ(t)，x)的符号已知，且不变号.另外，g(t，θ(t)，x)有界.不失一般性，假设

这里，b1和b2是未知正常数.

注1.从假设1可以看出，本文考虑的对象除了包含参数不确定外，还包含有界外部扰动.

注2.从假设1和2可以看出，对系统中的不确定参数，仅要求它是有界的，对它的变化情况并没有作任何限定.因此，本文的对象可以是快变的.

用yr(t)表示输出参考曲线，对其作如下假设:

假设3.yr(t)以及它的变化律(t)都是已知、光滑、有界的.

令

表示系统的输出跟踪误差.

本文的控制目标是:在假设1～假设3满足的条件下，针对被控对象(1)，设计控制律u，使得闭环系统的所有信号是全局有界的，同时，输出跟踪误差εy(t)始终满足如下约束:

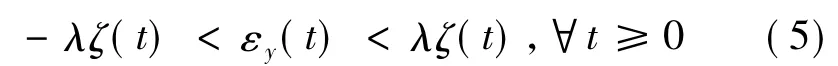
这里，λ为已知正常数，满足0＜λ≤1;ζ(t)表达式为:式中，a为正常数，ζ(0)＞ζ(∞)＞0.

注3.式(5)表明输出跟踪误差εy始终界于曲线λζ(t)和－λζ(t)之间.因此，通过合理选择 λ和ζ(t)可以确保输出跟踪误差εy满足期望的性能指标，例如超调大小、动态响应时间以及稳态误差等.

1.2 预备知识

在文献［8］中，作者引入一个坐标变换，将带性能约束的控制问题转化为无约束控制问题.下面进行简要介绍.

式(5)等价于

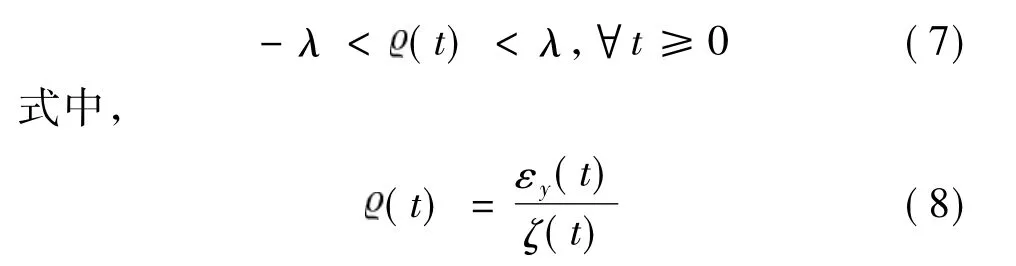
选取如下坐标变换:

容易知道，(1)当＞－λ，且 →－λ时，z→－∞;当

＜λ，且→λ时，z→+∞;(2)当z→0时，εy→0.

注4.当接近±λ时，也即输出跟踪误差εy接近式(5)定义的边界时，z将是无穷大.因此，如果设计控制律u，确保z是有界的，那么输出跟踪误差εy将始终满足约束(5).此外，如果z充分小，那么εy也将充分小.下一节就利用这个思想，设计控制器确保z是有界的.

2 主要结果

根据注4，本节将设计一个鲁棒自适应控制器，确保z和闭环系统的其他信号都是有界的，而且z的最终界只与控制器参数有关，与系统参数无关.因此，通过调节控制器参数，可使得z的最终界充分小.

需要说明的是，式(10)～(20)是在输出跟踪误差εy始终满足式(5)的前提下得到的.后续的引理1中，严格的稳定性分析表明:当初始状态满足式(5)的约束时，本文的方法可以确保输出跟踪误差εy始终满足式(5).

在式(9)中，对z求导，并将式(8)代入，得

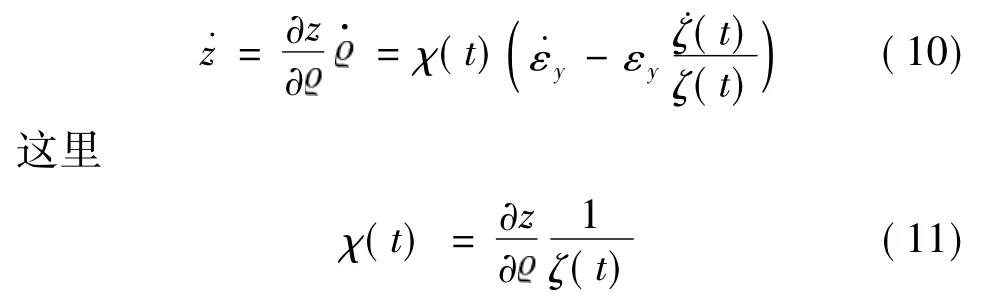
根据式(6)和式(9)，可知当εy满足式(5)时，有χ(t)＞0成立.

将式(4)代入式(10)中，并结合式(1)，得

其中，k＞0为正常数，F(t，θ(t)，x)定义如下:

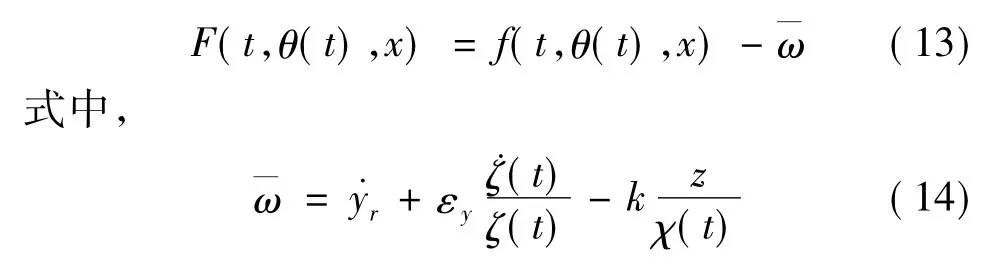
利用假设1，可知

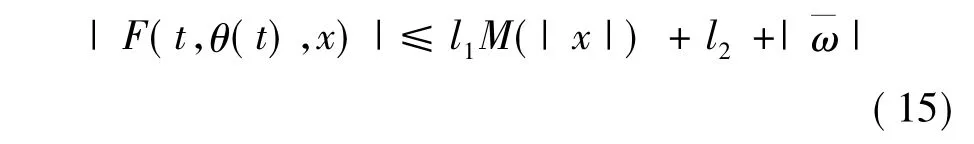
针对系统(12)～(15)，设计如下控制律和更新律

其中，sat(·)为饱和函数，定义如下:

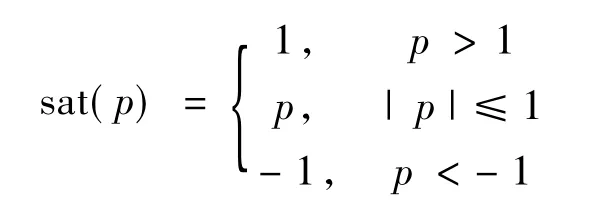
ε＞0和γi＞0(i=1，2，3)是设计参数.zΔ定义如下:

它可以看作是z到集合{z:|z|≤ε}的距离.

选取如下的Lyapunov函数:其中，zΔ在式(20)中定义，b1在假设2中定义，(i=1，2，3)定义如下:

这里，l1和l2在假设1中定义.

有如下的引理:

引理1.在假设1～假设3满足的条件下，针对被控对象(1)，设计控制律(16)和更新律(17)～(19).对任意的k＞0，γi＞0(i=1，2，3)，ε＞0以及满足式(5)的任意初始值x(0)，我们有如下结论:

(I)z有界;

(II)对所有的时刻t，均有

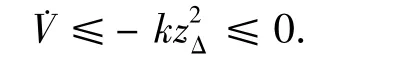
证明.首先，由于微分方程解的连续性，当初始状态x(0)满足式(5)的约束时，至少存在一个小的时间段，系统仍然满足约束;然后，证明在这个时间段内，由于控制的作用，系统不仅满足约束，而且不会靠近约束的边界.再利用微分方程解的延拓定理，可知整个时间段上系统都满足约束.

由于初始状态x(0)满足式(5)的约束，根据微分方程解的连续性和唯一性(参考［12］中的引理1)，存在一个时刻τmax＞0，使得当t∈(0，τmax］时，x(t)满足式(5)的约束.因此，在t∈(0，τmax］时间内，式(12)、(16)～(19)都是成立的.

由式(12)、(16)～(19)组成的闭环系统可知:当系统轨线位于区域|z|≤ε内，即zΔ=0时，(i= 1，2，3)保持不变.因此，李雅普诺夫函数也保持不变.即

在区域|z|≤ε外，也即zΔ≠0时，计算李雅普诺夫函数V沿闭环轨线式(12)，式(16)～(19)的导数，并注意到以及式(15)，有

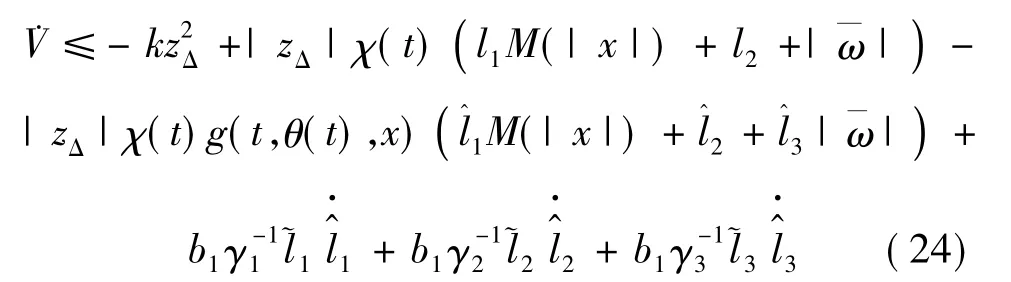
根据式(17)～(19)，χ(t)＞0和假设1，可知对所有的t∈(0，τmax］，均有(t)＞0(i=1，2，3)成立.因此，利用g(t，θ(t)，x)≥b1将式(24)进一步放缩

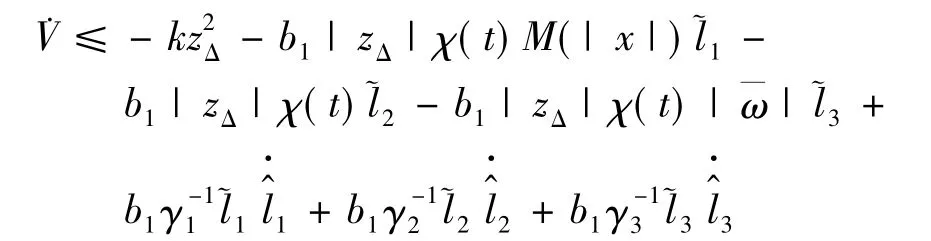
将式(17)～(19)代入式(24)，得

结合式(23)，可知当t∈(0，τmax］时，无论何种情况，均有

成立.式(25)表明V在t∈(0，τmax］上是有界的.又根据式(21)V的表达式，可知zΔ(t)在t∈(0，τmax］上也是有界的.再根据式(20)，可知z(t)在t∈(0，τmax］上是有界的.根据解的延拓定理(参考［12］中的引理1)，重复上述分析，可知在整个时间区间t∈(0，∞)上，z(t)都是有界的.因此，引理1的第一条结论是正确的.

进一步，由于在整个时间区间t∈(0，∞)上，z(t)都是有界的，因此，在整个时间区间t∈(0，∞)上，x(t)始终满足式(5)的约束.于是，闭环系统式(12)、(16)～(19)可拓展到整个时间区间上，也即在整个时间区间t∈(0，∞)上，闭环系统式(12)、(16)～(19)都是有定义的.相应地，式(25)的结论也可以拓展到整个时间区间上.因此，引理1的第二条结论也是正确的.

在引理1的基础上，我们得到如下定理:

定理1.在假设1－假设3满足的条件下，针对被控对象(1)，设计控制律(16)、(17)～(19).对任意的k＞0，γi＞0(i=1，2，3)，ε＞0以及满足式(5)的任意初始值x(0)，我们有如下结论:

(I)输出跟踪误差εy满足式(5)所给的约束;

(II)闭环系统的所有信号是全局有界的;

(III)存在正常数T*(ε)，使得当t＞T*时，有

成立.

证明.(I)根据引理1，可知z是有界的.根据注4，z的有界性确保了输出跟踪误差 εy(t)始终满足式(5)的约束.因此，结论(I)成立.

(II)x的有界性.由于εy(t)始终满足式(5)，显然εy(t)是有界的.再利用式(4)以及假设3，可知y，也即x是有界的.

l^i(i=1，2，3)的有界性.根据引理1，可知对所有的时刻t，均有

因此，V是有界的.根据式(21)中V的表达式，可知(i=1，2，3)是有界的.再根据式(22)，可知(i= 1，2，3)有界.

u的有界性.u的定义见式(16).首先证明的有界性，它的定义见式(14).由于z有界，根据式(9)，可知存在正常数μ，使得

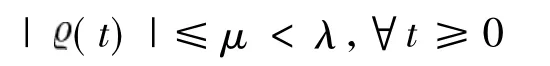
根据式(11)，易知存在正常数κ1和κ2，使得

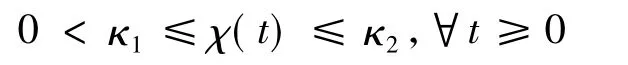
(III)考虑式(12)，根据χ(t)的有界性，F(t，θ(t)，x)的有界性，g(t，θ，x)的有界性(假设2)，u的有界性以及z的有界性，可知式(12)的右边是有界的，也即是有界的.根据式(20)zΔ的定义，在区域|z|≤ε内，zΔ≡0，因此≡0;在区域|z|≤ ε外，易知因此，的有界性确保了也是有界的.

对式(26)两边积分，得

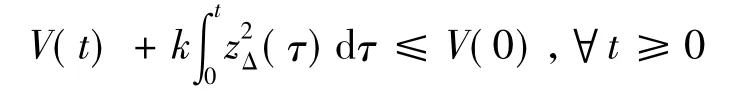
可知zΔ是平方可积的.同时有界，根据Barbalat引理［13］，可知zΔ→0，t→∞.因此，存在T*(ε)＞ 0，使得当t＞T*时，有.进一步，根据式(20)zΔ的定义，可知.因此，结论(III)成立.

注5.从定理1可以看出，本文的方法不仅确保输出跟踪误差满足给定的约束，同时，新的状态变量的最终界只与控制器参数ε有关，与原系统的参数无关.由于ε是已知的，因此我们可以较好的估计这个最终界.

3 数值仿真

下面通过一个例子来验证本文方法的有效性.

考虑如下对象:=θ1(t)x+θ2(t)u+d(t)，x(0)=2.这里θ1(t)=3+8sin(10t)，θ2(t)=10+ 7sin(10t)，d(t)=0.1sin(10t)+0.2.根据θ1(t)，θ2(t)的表达式可以看出，这两个参数都是快时变的.控制器设计的时候，我们不知道θ1(t)，θ2(t)以及d(t)的具体表达式，只知道|θ1(t)|≤12，2≤θ2(t)≤20以及|d(t)|≤0.5.根据式(1)～式(3)，可知l1=12，l2=0.5，b1=2以及M(|x|)=|x|.因此，

控制目标是跟踪如下参考系统的输出:

这里，参考系统的初始状态为［x1m(0)x2m(0)］=［0.50］，ω1=1，ξ1=0.95，um≡5.

关于跟踪误差的性能约束(见式(5)和式(6))，取ζ(0)=3，ζ(∞)=0.05，a=0.5以及λ=1.

仿真中，取k=10，ε=0.1，γi=10(i=1，2，3)，参数估计初始值取为

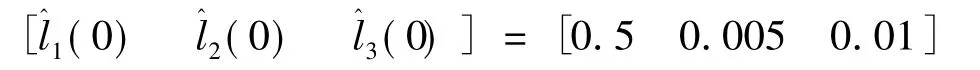
显然，参数估计初始值和真实值

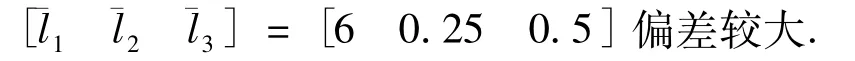
仿真结果如图1～4所示.从图1～4可以看出，系统的所有信号均是有界的，而且输出跟踪误差始终满足给定的约束.由于干扰的存在，系统到达稳态时，控制量也以一定的周期波动，也即控制律部分抵消了干扰的影响.因而本文的方法是有效的.

图1 输出曲线Fig.1 Output variables

图2 输出跟踪误差Fig.2 Output tracking errors

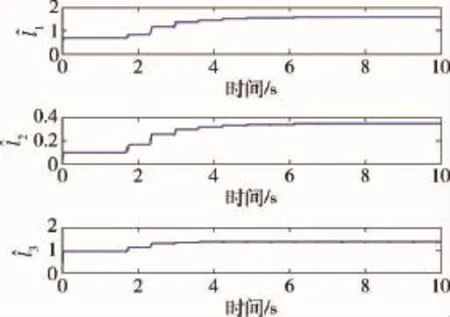
图3 参数估计值Fig.3 Parameter estimates

图4 控制量Fig.4 Control input

4 结论与展望

本文研究了一类存在有界干扰的快时变系统的确保性能跟踪控制问题.基于确保性能控制技术，通过引入一个状态变换，本文提出了一个确保跟踪性能的鲁棒自适应控制器.该控制器一方面确保了系统的输出跟踪误差始终满足给定的约束，另一方面还确保了这个新的状态变量所描述的系统也具有较好的性能.最后的仿真验证了本文方法的有效性.

当然，本文的结果仅仅针对一阶系统.后续的工作尝试将其推广到高阶系统.

［1］吴宏鑫，胡军，解永春.基于特征模型的智能自适应控制［M］.北京:中国科学技术出版社，2009.

［2］胡勇，徐李佳.基于一阶特征模型的一类快变系统的自适应控制［C］.第34届中国控制会议.北京:中国自动化学会控制理论专业委员会，2015.HU Y，XU L J.First-order characteristic model based on adaptive control for a class of systems with fast timevaring parameters［C］.The 34thChinese Control Conference.Beijing:Technical Committee on Control Theory，Chinese Association of Automation，2015.

［3］BARMISH B R.New tools for robustness of linear systems［M］.NewYork:Macmillan，1994.

［4］PUGA S，BONILLA M，MALABRE M.Singularly perturbed implicit control law for linear time varying SISO system［C］//The 49thIEEE Conference on Decision and Control(CDC).New York:IEEE，2010:6870-6875.

［5］PUGA S，BONILLA M，MALABRE M.Singularly perturbed implicit control law for linear time varying SISO system.part II:state observation［C］//The 50thIEEE Conference on Decision and Control and European Control Conference(CDC-ECC).New York:IEEE，2011: 1258-1263.

［6］ZHU Y，WEN C，SU H，et al.Adaptive modular control for a class of nonlinear systems with unknown timevarying parameters［C］//American Control Conference (ACC).New York:IEEE，2013:2631-2636.

［7］WANG L，ORTEGA R，SU H，et al.Stabilization of nonlinear systems nonlinearly depending on fast time-varying parameters:an immersion and invariance approach［J］.IEEE Transactions on Automatic Control，2015，60(2):559-564.

［8］WANG C，LIN Y.Decentralized adaptive tracking control for a class of interconnected nonlinear time-varying systems［J］.Automatica，2015，54:16-24.

［9］BECHLIOULIS C P，ROVITHAKIS G.Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance［J］.IEEE Transactions on Automatic Control，2008，53(9):2090-2099.

［10］KOSTARIGKA A K，ROVITHAKIS G.Prescribed performance output feedback/observer-free robust adaptive control of uncertain systems using neural networks［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B:Cybernetics，2011，41(6):1483-1494.

［11］BECHLIOULIS C P，ROVITHAKIS G.Robust partialstate feedback prescribed performance control of cascade systems with unknown nonlinearities［J］.IEEE Transactions on Automatic Control，2011，56(9):2224-2230.

［12］TEE K P，GE S S，TAY E H.Barrier Lyapunov functions for the control of output-constrained nonlinear systems［J］.Automatica，2009，45(4):918-927.

［13］SLOTINE J-J E，LI W.Applied nonlinear control［M］.Prentice-Hall Englewood Cliffs，NJ，1991.

Robust Adaptive Control for a Class of Uncertain Fast Time-Varying Systems with Prescribed Performance

LI Gongjun1，2
(1.Beijing Institute of Control Engineering，Beijing 100190，China;2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China)

A tracking control with prescribed performance is investigated for a class of uncertain one-order fast time-varying systems.Such control problem is firstly transformed into one without constraints by introducing a state transformation.Then，a robust adaptive controller is proposed.Our scheme can ensure not only that the systems satisfy the given performance constraints，but also the ultimate bound of the new state variable only depends on some control parameters.As the control parameters are known，this scheme can provide a good estimation of this bound.Finally，numerical simulations verify the validity of the proposed approach.

time-varying system;fast time-varying parameter;robust adaptive control;external disturbance;prescribed performance control

TP273

:A

:1674-1579(2016)01-0025-06

10.3969/j.issn.1674-1579.2016.01.005

李公军(1984—)，男，博士研究生，研究方向为高超声速飞行器控制研究.

*国家自然科学基金资助项目(61333008和61273153).

2015-08-20