二项式定理培优卷(B卷)
2018-05-31江苏省张家港职业教育中心校韩文美
■江苏省张家港职业教育中心校 韩文美
一、选择题
1.(a+b+c)9的展开式中,a2b3c4的系数为( )。
A.126 B.1260
C.1296 D.3024
2.(2x+x)4的展开式中x3的系数是( )。
A.6 B.12 C.24 D.48

A.7 B.6 C.5 D.4
4.已知(1+x)+(1+x)2+…+(1+x)n=a0+a1x+a2x2+…+anxn,若a0+a1+a2+…+an=30,则n=( )。
A.3 B.4 C.5 D.7
5.若(x+3y)n的展开式的系数和等于(3a+4b)10的展开式的二项式系数之和,则n的值为( )。
A.5 B.8 C.10 D.15
6.1.056精确到0.01的近似值为( )。
A.1.23 B.1.24 C.1.33 D.1.34
7.一串彩灯由灯泡串联而成,每串有20只灯泡,只要有1只灯泡坏了,整串灯泡就不亮,则因灯泡损坏致使一串彩灯不亮的可能性的种数为( )。
A.20 B.219
C.220D.220-1
8.已知实数x满足|x|<1,n是大于1的正整数,记a=(1+x)n+(1-x)n,则( )。
A.a<2nB.a>2n
C.a=2nD.a与2n的大小与n有关
9.( )。
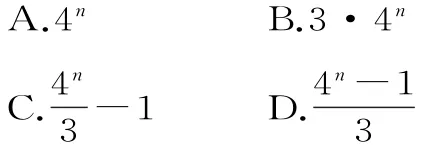
A.14 B.-14 C.42 D.-42
11.已知的展开式中常数项为1120,其中实数a是常数,则展开式中各项系数的和是( )。
A.28B.38
C.1或38D.1或28
12.已知(1-2x)6=a0+a1x+a2x2+…+a6x6,则|a0|+|a1|+|a2|+…+|a6|的值为( )。
A.1 B.64 C.243 D.729
13.在(1-x3)(1+x)10的展开式中,x5的系数是( )。
A.-297 B.-252
C.297 D.207
14.若n∈N*,(2+1)n=2an+bn(an,bn∈Z),则bn的值( )。
A.一定是奇数
B.一定是偶数
C.与n的奇偶性相反
D.与n有相同的奇偶性
15.9192被100除所得的余数为( )。
A.1 B.81 C.-81 D.9
16.数11100-1的末尾连续出现零的个数是( )。
A.0 B.3 C.5 D.7
17.已知=am+am+1+…+an(其中m,n∈Z,且0≤m<n),若
A.0
B.-2
C.(-1)n
D.n为偶数时值为0,n为奇数时值为-2
18.设P=1+5(x+1)+10(x+1)2+10(x+1)3+5(x+1)4+(x+1)5,则P等于( )。
A.x5B.(x+2)5
C.(x-1)5D.(x+1)5
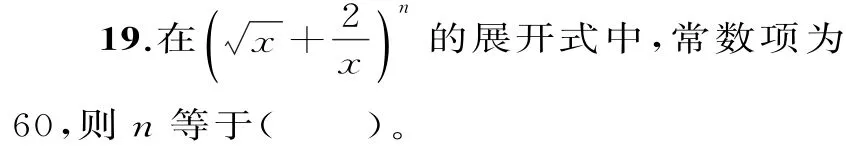
A.3 B.6 C.9 D.12

A.16 B.70 C.560 D.1120
21.设(2x-3)4=a0+a1x+a2x2+a3x3+a4x4,则a0+a1+a2+a3+a4=( )。
A.1 B.2 C.3 D.4
22.设n为自然数,则=( )。
A.-1 B.0 C.1 D.2n
23.在(1+x)3+(1+x)3+(1+3x)3的展开式中,x的系数为( )。
A.5 B.6 C.7 D.8
24.在(x2-2x+1)4的展开式中,x7的系数是( )。
A.8 B.7 C.-7 D.-8
25.在(4x-2-x)6的展开式中,常数项为( )。
A.14 B.15 C.16 D.17
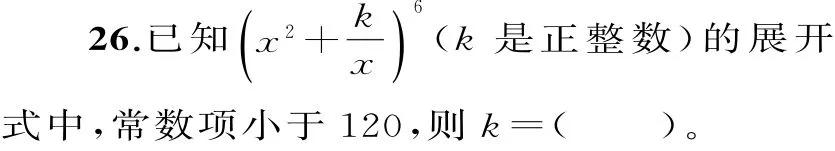
A.1 B.2 C.3 D.4
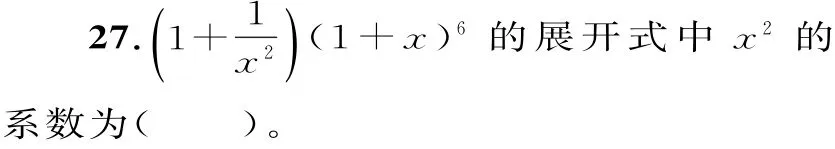
A.15 B.20 C.30 D.35
28.(x+y)(2x―y)5的展开式中x3y3的系数为( )。
A.―80 B.―40 C.40 D.80
29.已知(1+3x)n的展开式中含x2项的系数是54,则n=( )。
A.3 B.4 C.5 D.6
30.已知多项式(x+1)3(x+2)2=x5+a1x4+a2x3+a3x2+a4x+a5,则a4+a5=( )。
A.20 B.21 C.22 D.23
31.若(2x+3)4=a0+a1x+a2x2+a3x3+a4x4,则(a0+a2+a4)2-(a1+a3)2的值为( )。
A.1 B.-1 C.0 D.2

A.2 B.0 C.-1 D.-2

A.32 B.34 C.36 D.38
34.在(2x-3y)10的展开式中,奇数项系数和为( )。
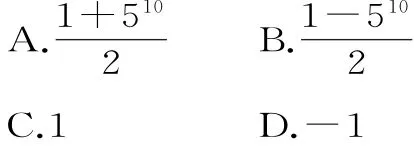
35.若第6项,设(1-3x)n=a0+a1x+a2x2+…+anxn,则a1+a2+…+an的值为( )。
A.254 B.255 C.256 D.257
36.若a1(x-1)4+a2(x-1)3+a3(x-1)2+a4(x-1)+a5=x4,则a2+a3+a4=( )。
A.12 B.13 C.14 D.15
37.若的绝对值之和为1024,则展开式中x的一次项的系数为( )。
A.12 B.-13 C.14 D.-15
38.由等式x4+a1x3+a2x2+a3x+a4=(x+1)4+b1(x+1)3+b2(x+1)2+b3(x+1)+b4,定义映射f:(a1,a2,a3,a4)→(b1,b2,b3,b4),则f(4,3,2,1)等于( )。
A.(1,2,3,4) B.(0,3,4,0)
C.(-1,0,2,-2) D.(0,-3,4,-1)
二、填空题
39.若(x+1)n=xn+…+ax3+bx2+cx+1(n∈N*),且a∶b=3∶1,那么n=____。
40.若(ax-1)5的展开式中x3的系数是-80,则实数a的值是____。
41.已知二项式(3x+2)n的展开式中所有项的系数和为3125,则此展开式中x4的系数是____。

44.若在二项式(x+1)10的展开式中任取一项,则该项的系数为奇数的概率是____。(结果用分数表示)
45.若(1+2)5=a+b2(a,b为有理数),则a+b=。
46.已知)n的展开式中各项系数的和是128,则展开式中x5的系数是____。(以数字作答)
47.设(x+1)4(x+2)5=a0+a1(x+3)+a2(x+3)2+…+a9(x+3)9,那么(a0+a2+a4+a6+a8)2-(a1+a3+a5+a7+a9)2=____。
48.已知(1+x)+(1+x)2+…+(1+x)n=a0+a1x+a2x2+…+anxn,若a1+a2+…+an-1=509-n,则n的值为____。
49.若(1-2x)2018=a0+a1x+a2x2+…+a2018x2018(x∈R),则(a0+a1)+(a0+a2)+(a0+a3)+…+(a0+a2018)=____。(用数字作答)
50.(x2-4x+4)5的展开式中x的系数是____。
51.今天是星期四,再过260天后的第一天是星期____。
52.计算某项税率,需用公式y=(1-5x)n(n∈N*),现已知y的展开式中各项的二项式系数之和是64,用四舍五入的方法计算当x=时y的值,若精确到0.001,其千分位上的数字应是____。
53.已知(1+x)n的展开式中,第2,3,4项的系数顺次成等差数列,则展开式中含x2的项的系数为____。

57.1+3+32+…+399除以4的余数为____。
三、解答题
58.已知(xlgx+1)n的展开式中,末三项的二项式系数和等于22,二项式系数最大项为20000,求x的值。
59.设(3x-1)6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0,求a6+a4+a2+a0的值。
60.若(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11,求:
(1)a1+a2+a3+…+a11;
(2)a0+a2+a4+…+a10。
61.(1)求使2n-1能被7整除的所有正整数n;
(2)证明:对于所有的正整数n,2n+1均不能被7整除。
62.在二项式(axm+bxn)12(a>0,b>0,m、n≠0)中有2m+n=0,如果它的展开式里最大系数项恰是常数项。
(1)求它是第几项;
(2)求的取值范围。
