借助函数零点巧求最值

☉山东省肥城市泰西中学 常芳源

借助函数零点巧求最值

☉山东省肥城市泰西中学 常芳源

利用导数研究函数的最值问题是高考常考题型之一，解答此类问题的基本策略是：先求函数的单调区间，进而求出函数的极值，再与区间端点的函数值进行比较，从而确定最值.但某些问题的求解中，最值存在的条件并不确定，如：在区间［a，+∞）内单调递减的函数，是不是就不存在最小值呢？此时就需要我们深入挖掘隐含条件来探究问题.其中函数的零点在问题的求解中起到了重要的作用，下面简举两例进行分析.

（Ⅰ）求f（x）的单调区间；

（Ⅱ）若f（x）在［0，+∞）上存在最大值和最小值，求a的取值范围.

说明：函数单调区间的求解，常伴随着对参数的讨论，分类的标准是先看最高次项的系数是否含有参数，若有，则分参数等于0、大于0、小于0三种情况.其次判断导函数的零点个数.当含有两个零点时，若两个零点的大小不确定，需要再次进行分类讨论.最后根据零点左右两侧导数符号的正负，得出函数的单调区间.

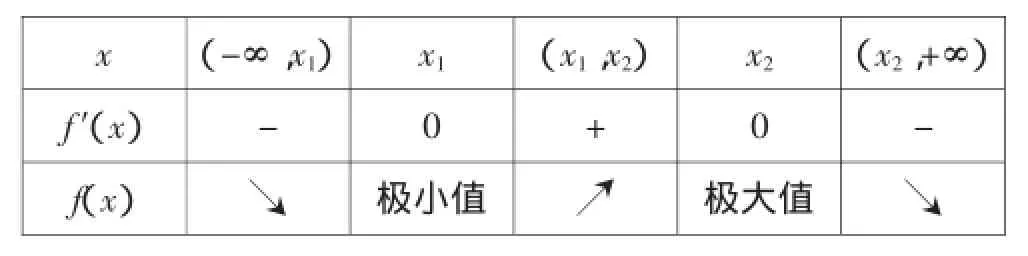
x（-∞，x1）x1（x1，x2）x2（x2，+∞）f′（x）-0+0-f（x）↘极小值↗极大值↘

③当a＜0时，f（x）与f′（x）随x的变化情况如下表：

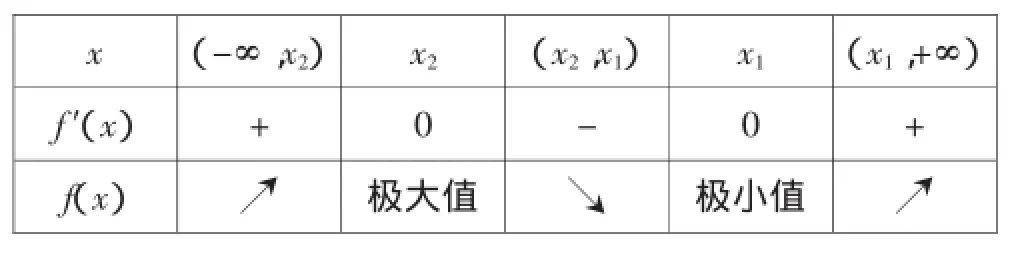
x（-∞，x2）x2（x2，x1）x1（x1，+∞）f′（x）+0-0+ f（x）↗极大值↘极小值↗

说明：最值问题的求解是以函数单调性为基础.第（Ⅰ）问已经判断出函数的单调区，故可在此基础上讨论函数的最值问题.

（Ⅱ）由（Ⅰ）知，a＝0时不符合题意.当a＞0时，由（Ⅰ）知，（fx）在（0，）内单调递增，在（，+∞）内单调递减，所以（fx）在（0，+∞）上存在最大值f（）＝a2＞0.

同理当a＜0时，易求得函数f（x）的最小值.因为函数在（-a，+∞）内单调递增，从直观上看，函数不存在最大值.挖掘隐含条件易求得函数的零点，且唯一.又易判断x0＜-a，所以函数在（-a，+∞）内不存在零点，而最小值f（-a）＜0，因此可判断在区间（-a，+∞）内，f（x）＜0恒成立.从而找到取得最大值的条件.

续解：设x0为（fx）的零点，易知，且当a＞0时，.从而x＞x时，（fx）＞0；x＜x时，（fx）＜0.00

若f（x）在［0，+∞）上存在最小值，必有f（0）≤0，解得-1≤a≤1.

所以当a＞0时，若f（x）在［0，+∞）上存在最大值和最小值，则a的取值范围是（0，1］.

当a＜0时，由（Ⅰ）知，f（x）在（0，-a）内单调递减，在（-a，+∞）内单调递增，所以f（x）在（0，+∞）上存在最小值f（-a）＝-1.

若f（x）在［0，+∞）上存在最大值，必有f（0）≥0，解得a≥1，或a≤-1.

所以当a＜0时，若f（x）在［0，+∞）上存在最大值和最小值，则a的取值范围是（-∞，-1］.

综上所述，a的取值范围是（-∞，-1］∪（0，1］.

至此问题得到圆满解决.再看下列：

（Ⅱ）当a＞0时，证明：存在实数m＞0，使得对于任意的实数x，都有|f（x）|≤m成立.

说明：本题第（Ⅰ）问较为基础，属于送分题.第（Ⅱ）问证明不等式恒成立，此类问题通常转化为求函数的最值问题，欲证|f（x）|≤m（m＞0）恒成立，即求不等式左边的最大值，但是因为有绝对值符号的存在，|f（x）|最大值的取得既可能是f（x）的最大值，也可能是f（x）的最小值，因此问题等价于求函数f（x）的最大值和最小值.

当x变化时，f′（x）与f（x）的变化情况如下表：

x（-∞，x1）x1（x1，x2）x2（x2，+∞）f′（x）+0-0+ f（x）↗极大值↘极小值↗

所以函数f（x）在（-∞，x1），（x2，+∞）上单调递增，在（x1，x2）上单调递减.

说明：函数f（x）在（-∞，x1），（x2，+∞）上单调递增，从表面上看不存在最大值和最小值.但挖掘隐含条件不难发现函数的零点为x＝1，且唯一存在，则函数在区间在（-∞，x1），（x2，+∞）上不存在零点.通过比较知x＝1在两极值点之间，因此结合函数的单调性可知极大值大于0，极小值小于0，进而得知在区间（-∞，x1）内，f（x）＞0恒成立，在区间（x2，+∞）内，f（x）＜0恒成立.所以函数f（x）的极大值即为函数的最大值，极小值即为函数的最小值.

说明：此时分别求出函数的极大值与极小值后，需要比较极大值与极小值的绝对值的大小关系，则较为困难，因此陷入解题误区.重新审视题目条件“当a＞0时，证明：存在实数m＞0，使得对于任意的实数x，都有|f（x）|≤m成立”，并不是要求m的取值范围，因此只要能够证明函数f（x）存在最大值和最小值即可，因此可按如下作答：

续解：记M＝max｛|f（x1）|，|f（x2）|｝，其中max｛|f（x1）|，|f（x2）|｝为两数|f（x1）|，|f（x2）|中最大的数.综上所述，当a＞0时，存在实数m∈［M，+∞），使得对于任意的实数x，不等式|f（x）|≤m恒成立.

通过上述两题的解答，不难发现题目条件中自始至终都没有提到零点，但最值存在条件的判定中零点的作用功不可没.因此解答此类问题时要全面考虑，单调区间、极值、零点不可偏废.Z