浅谈以形辅数在不等式教学中的设计

☉浙江省淳安中学 朱胜平

浅谈以形辅数在不等式教学中的设计

☉浙江省淳安中学 朱胜平

华罗庚先生对中学数学思想方法推崇至极的是数形结合思想，其认为能站在不同的视角审视同一个数学问题，是提高学生思维和开拓眼界最好的表现.众所周知，数形结合思想有以形辅数和以数解形两个不同的方面，一种是用几何的方式巧妙地解决代数问题，另一种是用代数方法运算几何问题的结论.从笔者多年教学经验来看，以形辅数对于学生思维的培养是发散的，其有助于灵活地转换视角思考问题；而以数解形却恰恰相反，用了更为全面的方式去解决几何问题，是全面性思维的一种体现，举一个例子，比如直线和圆的问题，从几何图形中思考往往只能想到一种情况、一个答案，但是从代数方式去解决，我们发现代数方法能非常全面地解决图形中没能作出的情况，这正是以数解形的优点.

那么如何对高一学生去渗透数形结合思想中的以形辅数呢？在新知教学中如何实施这一教学呢？教师如何去设计这样的课堂教学呢？带着这一想法，笔者以一元二次不等式的初高中衔接内容为本，进行一种设计与尝试.

一、设计前瞻

1.教学内容

本节课的内容承接了上一节课解一元二次不等式的基本内容，理解三个“二次”之间的关系.因此，巩固三个“二次”之间的关系和进一步掌握一元二次不等式解法非常重要.本节课用特殊到一般的方式，推导出任何情况下求解一元二次不等式的方法.

2.涉及思想

一元二次不等式贯穿整个高中数学，作为一个基础性的工具使用，解决大量的数学问题.在本单元中，第二课时将不等式各情况下的解法进行化归，掌握这些对快速求解不等式十分有帮助，并在这个过程中培养学生数学结合的思想.

3.设计思考

在第一节课的基础上，对一元二次不等式进行拓展，再通过对其化归，找到求解任何情况下一元二次不等式的基本方法.利用数形结合，让学生体会数学知识间的相互联系，明白不等式的问题也可以通过相应函数图像来解决.

二、设计目标

1.知识与技能视角

（1）进一步熟练掌握解一元二次不等式的解法；（2）巩固三个“二次”之间的关系，并利用这种关系求解相关问题，培养学生数形结合的应用意识.

2.过程与方法视角

（1）通过数形结合解决不等式问题；（2）在解决一元二次不等式过程中，让学生体会分类讨论的理解和应用.

3.情感态度价值观视角

激发学生学习数学的热情，培养其勇于探索、敢于创新的精神.

三、设计过程

（一）复习引入

问题1：一元二次方程、一元二次不等式与二次函数的关系？

①二次函数图像在x轴上方部分对应的x值为一元二次不等式大于0的解；

②二次函数图像与x轴的交点的横坐标是一元二次方程的根；

③一元二次不等式解集对应的端点是一元二次方程的根.

问题2：上一节课中，我们如何求一元二次不等式ax2+bx+c＞0（a＞0）的解集？

第一步：求对应方程ax2+bx+c＝0（a＞0）的判别式.

第二步：根据判别式求方程的根.

①若Δ＞0，则不等式的解集为｛x|x＜x1，或x＞x2｝；

②若Δ＝0，则不等式的解集为｛x|x≠x1｝；

③若Δ＜0，则不等式的解集为R.

（二）新课设计

例1已知方程4x2-4x＝15的解为-，，快速给出不等式4x2-4x＞15的解集.

设计意图：通过这道例题热身，再一次明确方程、不等式和函数之间的关系，做好复习并为下面做好铺垫，巩固学生求ax2+bx+c＞0（a＞0）的能力.

学生：回忆上节课表格内容，给出正确答案.

例2解不等式-6x2-x+2≤0和-2x2+x＜-3.

设计意图：第一课时所解的不等式二次项系数a＞0，在引导之下，让学生产生如何求解a＜0的疑问，丰富一元二次不等式的内容，也帮助学生扩散思维，并在类比和化归中自己探索出求解方法.

师生活动：

教师：提出问题.

学生：思考，类比解决或者转化问题.

师生：要求学生自己发现规律，发表自己的看法，老师引导整理出规范的步骤.

教师：上一节课，我们只接触了二次项系数a＞0的一元二次不等式的求解问题，想必也有同学对如何求解二次项系数a＜0的一元二次不等式有疑问.既然如此，我们一起来探究a＜0时的求解方法.

学生：探索研究，讨论交流.方法一：通过对不等式移项，将二次项系数a＜0的一元二次不等式转化成a＞0的形式，利用上节课的内容求解；方法二：类比上节课的方法，将a＜0时的函数图像画出，根据图像求解不等式的解集.

教师：对两种方法进行评价和肯定.方法一，利用了化归思想，一旦遇到一元二次不等式的题目都转化成a＞0的形式进行求解；方法二，利用类比a＞0的形式，通过对一元二次不等式、一元二次方程和二次函数的关系，进一步得到a＜0时的表格，巩固了三者关系的知识.为了方便理解和计算，教师引导学生采用第一种方法.

设计意图：这两节课接触的一元二次不等式一般都是二次项系数a＞0并且a为整数的类型，通过这题让学生充分理解化归的思想，并且在他们脑海中形成一种模式，即所有一元二次不等式都可以转化成a＞0且a为整数的形式进行求解.

教师：提出问题，让学生回答解题思路.

师生：讨论，在已有的认知基础上提出自己的想法.方法：将上述不等式转化成a＞0且a为整数的形式进行求解.

学生：原不等式为x2-2x-4＜0，再根据一般求解步骤求不等式的解集.

教师：根据刚才的几个题目，结合上节课的内容，请同学们整理出求一元二次不等式的一般步骤.

学生：①化，将不等式化成一般形式；②判，判断对应方程有没有根；③求，求出方程的根；④画，画出对应函数图像；⑤解，根据图像写出不等式的解集.

（三）拓展升华

练习1设m∈R，解关于x的不等式m2x2+2mx-3＜0.

设计意图：这是解含参数的不等式的题目.本节课的重点是将一元二次不等式进行推广，从a＞0的形式推广到a取任意值的情况.这题重点在于讨论m的取值，通过值的不同，结合二次函数图像求解.

师生活动：

教师：找学生板演，巡视课堂，答疑解惑.

学生：独立完成.

师生：共同批改板演学生的答案，同时指出可能出现的错误，提醒学生注意.

易错点1：忽略m＝0的情景，直接将不等式默认为一元二次不等式，忽略部分答案.

变式训练1：解关于x的不等式ax2-（2a+1）x+2＜0.

小结1：解含参数的一元二次不等式时，首先要讨论二次项系数，再根据一般步骤求解.

练习2若a＞0，则关于x的不等式x2-4ax-5a2＞0的解集是__________.

设计意图：同样是含有参数的练习题，但是本题的重点在于三个“二次”之间的关系，利用这种关系求解不等式的解集，特别要注意判断两个根的大小.

师生—共同讨论回忆三个“二次”之间的关系，并利用这种关系求解.

①方程x2-4ax+5a2＝0的根为：5a和-a；

②因为a＞0，所以5a＞-a，即x1＝-a，x2＝5a；

③a＞0，开口向上，则大致图像如右

图所示；

④根据图像可知，不等式的解集为｛x|x＜-a或x＞5a｝.

变式训练2：已知不等式ax2-bx-1≥0的解集为］，则不等式x2-bx-a＜0的解集为_________.

小结2：三个“二次”之间的关系十分紧密，讨论一元二次方程和一元二次不等式时，要利用相应的二次函数解决问题，关系如下：

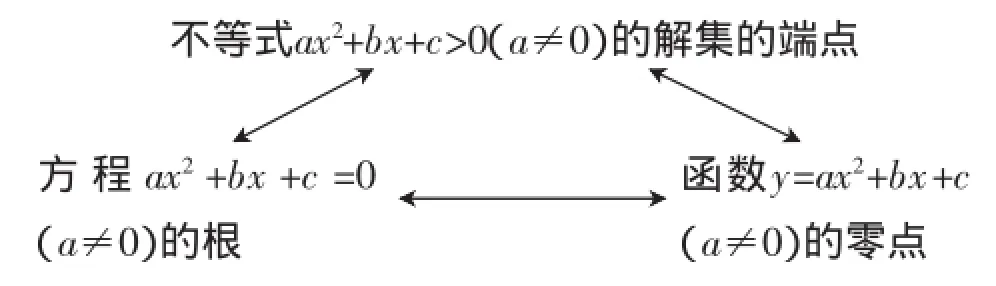
练习3若不等式ax2+2x-1＜0的解集为R，则实数a满足什么条件？

设计意图：本题暗含着恒成立的思想，通过数形结合，解得相应参数的取值范围.

师生：共同探讨a变化时，对应函数图像的变化.

①a＝0，对应函数为一次函数；

②a＞0，二次函数开口向上；

③a＜0，二次函数开口向下.

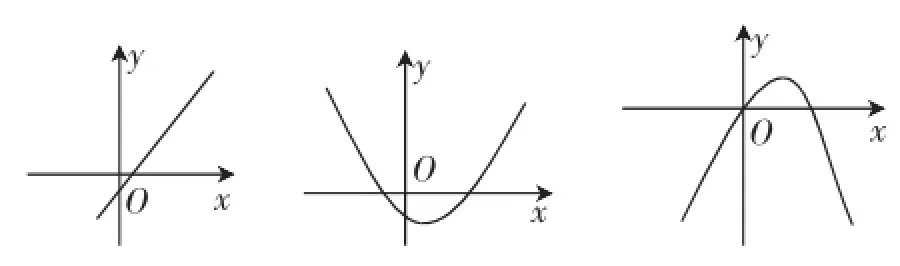
学生：通过上述三个图像，很容易得出只有a＜0符合条件.进而通过相应的三个图像求出满足条件的a的取值范围.（图略）

变式训练3：不等式（a-2）x2-2（a-2）x-4＜0恒成立，求a的取值范围.

小结3：求解简单的恒成立问题时，通过分析相应的函数图像可以求出所需要的式子，进而求解.数形结合是解决这类问题的最便捷的工具.

四、设计思考

本课是笔者以“以形辅数”作为指导思想设计的一堂新知教学课，从课堂初始提出的一元二次不等式开始，至始至终围绕着二次函数图像去思考如何解决不等式问题.从教学初始来看，笔者发现学生对于不等式、方程都是函数的特殊情形认知并不充分，没有完全将三者是一个统一体联系在一起，通过以形辅数的实践，学生渐渐认知要解决中学数学中最基本的一元二次不等式，主要问题是围绕图像展开的一种思考，与函数图像和x轴的交点（即方程的根有重要联系）.

在本课设计中，笔者处处请学生思考代数问题的解决是如何通过图像去展示的，从图像的角度去体会不等式是如何解决的，这种思想贯穿课堂教学的始终.从上述课堂教学也给笔者带来了一些小小的思索：

（1）图形直观性永远是解决问题最好的方式，从学生认知特点来看，直观依旧是其认知最好的方式，任何形态下能利用直观解决的问题，笔者始终坚持以形辅数；

（2）学生自学为主，教师为主导，通过传统的复习使学生温故而知新，拓宽了学生对一元二次不等式求解的系统认识；

（3）数形结合思想深入人心，根据三个“二次”之间的关系，通过对二次函数的分析，进一步求解一元二次不等式，尤其在含有参数的不等式中极为有用.

1.黄一燕.翻转课堂中数形结合教学设计模式研究［J］.数学教学与学习，2013（12）.

2.殷康康.不等式教学中以形辅数的运用与思考［J］.中学教研，2013（3）.Z