让高中数学课堂更有数学味道——一节《圆的切线问题》教学实录

☉湖北省武汉中学 蒋怡

让高中数学课堂更有数学味道
——一节《圆的切线问题》教学实录

☉湖北省武汉中学 蒋怡

我有幸参加了武汉市骨干教师课堂设计研修班的学习，能够和武汉市6位特级老师面对面学习交流，收获颇多.其中有着70岁高龄的数学特级教师田化澜一直教导我们：“数学课堂，老师一定要讲出数学的味，数学的道，数学的美.”数学的美我们体会颇多，一般反映在简明美、对称美、奇异美、序列美等方面.那“数学课堂的味道”又是什么？

结合数学的本质及数学教学的本质，我认为“数学的味道”应该体现数学的抽象性、推理性、探索性、问题性及数学语言表达等特点.我从教学实践中体会到，课堂上要具有数学味道，就应该把数学教学放在思想与意义的长河之中，不是单纯的数学知识与技能记忆的训练，而是通过数学教学，让学生在掌握知识和技能的过程中，学会用数学的思想方法思考，学会用数学的思维方式观察.那么，数学课如何上出“数学的味道”来呢？我以自己《圆的切线问题》一节课的课堂实录及教学反思，来和同行们探讨.

一、教学过程简录

1.问题引导，经历数学探索的味道

问题1：已知圆的方程是x2+y2=r2，求经过圆上一点M（x0，y0）的圆的切线方程.

（学生动笔，老师巡视，请一名已有解题思路的同学在黑板上完整解答.）

同学1：如图1，设所求直线方程的斜率为k，则点斜式写出直线方程为y-y0=k（x-x0），即kx-y+y0-kx0=0.①

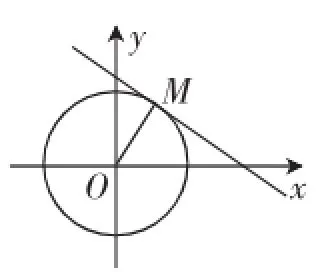
图1

化简整理②式得（r2-）k2+2x0y0k+r2-=0.

这位同学写到这儿，发现不容易求解k，一筹莫展.

同学2：这种求切线斜率方法太麻烦了，可以利用切点与圆心的连线与切线垂直，直接得到切线斜率为，所以经过点M的切线方程是，整理得x0x+y0y=+

因为点M在圆上，所以x0x+y0y=r2.

（不少同学在下面点头赞同）

教师：同学1是利用直线与圆相切的几何判定——圆心到直线的距离等于半径，用方程的思想求解k，因为方程中字母较多，求解k有一定的难度；同学2巧妙借助于圆上切点的性质，很快得到切线斜率，点斜式写出切线方程，很好.

问题2：虽然同学1的解答不是很简洁，但我在下面巡视时发现，这也是部分同学第一直观做法，同样解答到这儿的困难是求解k，你能帮助他们继续完成此题吗？

（给出2分钟思考后，我让解决了此问题的同学谈谈是怎么想的）

同学3：这个关于k的二次方程的系数与x0，y0，r有关，为了方便因式分解，我利用点M在圆上的条件代换得到

教师：这位同学很善于观察思考，利用等量代换减少方程中变元个数，使问题变得更清晰，易解答.

问题3：请同学们思考，以上同学解答过程严谨吗？

（立马有同学举手）

同学4：用点斜式写直线方程时，不含与x轴垂直的直线，所以还需分类讨论.他们求出的k=-，是在y≠0

0前提下解答的，当y0=0时，x0=±r，也适合x0x+y0y=r2，只有分类讨论后解答才算严谨的.

教师：非常好，这也是我们平时作业中的易错点，同学们要注意用点斜式写直线方程的局限性，要分斜率存在或不存在两种情况讨论，分类讨论也是数学中常见的一种数学思想.

问题4：切点与圆心的连线与切线垂直的条件，能否不用两直线斜率乘积为-1表示，进而也可以求出直线方程？

（学生纷纷回答，可以用向量的数量积为0来说明两直线垂直的关系，我于是请一个成绩中等学生回答）

同学5：这个题还可以用向量的方法来解决，更简洁！

如图2，设切线上任一点P的坐标为P（x，y），

所以x0·（x0-x）+y0·（y0-y）=0

故所求的直线方程为x0x+y0y=r2.

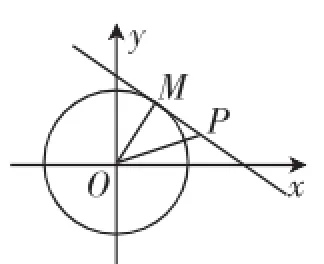
图2

教师：两直线垂直用直线的方向向量的数量积为0表示，其优点在于不用考虑直线的斜率是否不存在，这样可以避免分类讨论.这种解法的实质是利用直线l上任一点的坐标P（x，y）满足·=0的关系而得的.请同学们思考一下与有何关系？

问题5：是否还有解决问题1的方法？

得所求的直线方程为x0x+y0y=r2.

（同学们此时情不自禁喊，用向量数量积的几何意义解好简洁啊！）

教师：大家体会到了向量这个工具给我们解决问题带来的方便，很爽吧！它的实质还是数形结合，这是高中数学的一个重要的思想方法.大家再观察所得的直线方程，与圆的方程有无关联？

同学8：结构上很形似，圆中的x，y由二次变成了直线中的一次.

教师：大家可这样记忆过圆心为坐标原点的圆上一点的切线方程：将圆方程中的x2拆成x·x，其中一个x变成x0，y2拆成y·y，其中一个y变成y0，常数项不变.

请同学们思考，你能类比写出圆心不在原点，过圆上一点的圆的切线方程吗？

（趁热打铁，提出新的问题）

2.猜想验证，展现数学发展的味道

问题6：（1）若圆O的方程为标准方程（x-a）2+（y-b）2= r2，求过圆上一点M（x0，y0）的圆的切线方程；

（2）若圆O的方程为一般方程x2+y2+Dx+Ey+F=0（D2+ E2-4F＞0），求过圆上一点M（x0，y0）的圆的切线方程.

请同学们先类比猜想，再证明.

第一个问题同学们很快类比猜想出，过圆O：（x-a）2+（y-b）2=r2上一点M（x0，y0）的切线方程为（x0-a）（x-a）+（y0-b）（y-b）=r2，并利用·=r2得以证明.

第二个问题对切线方程猜想五花八门：

同学2：肯定不正确，因为这时x，y必须大于等于0.

同学3：猜想是x0x+y0y+Dx0+Ey0+F＝0，自己也不敢肯定，

教师：圆的一般方程中出现了x，y的一次项，不能类比x，y的二次项来猜测，那我们推导一下吧.你选择证明问题1的哪种方法？

教师：我们在这个问题中采用了先猜想，再论证的方法.数学猜想是推动数学理论发展的强大动力，是创造数学思想方法的重要途径.如欧拉猜想，哥德巴赫猜想，周氏猜测等等.这些猜想有的被验证为正确的，并成为定理；有的被验证为错误的；还有一些正在验证过程中.实现猜想的途径，可以是探索试验、类比、归纳、构造、联想等.当然，数学猜想是有一定规律的，如类比的规律、归纳的规律等，并且要以数学知识和经验为支柱，最后都要去验证它的正确性.正所谓“大胆地猜想，小心地论证”.

3.变式探究，体验数学思考的味道.

问题7：如图3，已知点M（x0，y0）为圆O：x2+y2=r2外一点，过点M作圆的切线MA，MB，其中A，B为切点，求切点弦AB所在的直线方程.

图3

（让同学们以小组形式讨论）

同学1：我们发现直线AB与直线OM垂直，直线AB的斜率好表示出来，但想求出A点坐标，有困难.借助于|MA|=|MB|的条件，联想将直线AB看作两相交圆的公共弦所在的直线.

再观察，知MA⊥OA，MB⊥OB，推出|MA|=|MB|.

所以A，B，M三点共圆.AB是以M为圆心，

半径为|AM|的圆与已知圆x2+y2=r2的公共弦.

同学2：还可以简单一点.由题意知MA⊥OA，MB⊥OB，

所以O，A，M，B四点共圆，且OM为此圆的直径，即圆O′：

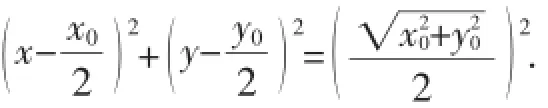
又AB为圆O、圆O′的公共弦，两圆方程相减，得切点弦AB所在直线方程为x0x+y0y=r2.

教师：同学们根据圆的切线长的性质，抓住了切点弦AB所在直线即为两相交圆的公共弦所在直线求解，很简洁.我在巡视时，看到有的同学也利用直线AB与直线OM垂直，得到直线AB的斜率，但想求出A点坐标，困难很大，能否对于A，B坐标设而不求，借助于问题1的结论求解呢？

同学3：设A（x1，y1），B（x2，y2），

由问题1结论得，切线MA方程为x1x+y1y=r2，切线MB方程为x2x+y2y=r2.

即A（x1，y1），B（x2，y2）两点坐标都满足关于x，y的二元一次方程x0x+y0y=r2，而过A，B两点的直线有且只有一条，因此，切点弦AB所在直线方程即为x0x+y0y=r2.

教师：这种直线与曲线相交，对于交点设而不求的方法确实不容易想到，这种方法我们在后面学习解析几何时要常常用到.我们发现点在圆外时，过此点作圆的两切线，所得到的切点弦方程与过圆上一点的圆的切线方程结论一模一样，很有意思吧.既然如此，我们能否另辟途径，求切点弦AB所在直线方程？

教师：这个联想不错，大家试试看.

（紧张思考与计算后，同学们脸上露出了笑容，我请一位同学讲讲做法）

同学5：连接OA，OB，OM，则MA⊥OA，MB⊥OB，且OM垂直平分AB.设AB与OM相交于T，任取直线AB上一点P，则在方向上的投影是|OT|.因为|OT|·|OM|= |OA|2=r2，所以·=r2，AB所在直线方程即为x0x+y0y=r2.

教师：我们再次感受到向量这个工具的强大，正因为存在着MA⊥OA，OM⊥AB这两种垂直关系，利用射影定理和向量数量积的几何意义才巧妙得到直线方程.

4.发散思维，挖掘出数学的内在味道

问题8：若M（x0，y0）是圆O：x2+y2=r2上一点，则直线x0x+y0y=r2与圆O：x2+y2=r2的位置关系如何？

教师：我改变点M与圆O的位置关系.

问题9：若M（x0，y0）是圆O：x2+y2=r2内一点，则直线x0x+y0y=r2与圆O：x2+y2=r2的位置关系如何？你能画出这条直线吗？

同学：因为点M（x0，y）0在圆x2+y2=r2内，所以满足+＜r2.

还可以知此直线与直线OM垂直，我在想这条直线位置能唯一确定吗？

教师：这个同学提出一个很好问题，大家想想，这条直线位置唯一确定吗？

同学：直线方程中x，y的系数和常数项已经给定，所以直线是唯一确定的.

（学生分组讨论，我参与其中，最后请作出图形的一组同学上台一边讲自己小组探索的过程，一边作出图形）

同学：我们从结论入手分析：P点肯定在与直线OM垂直的某一条直线l上，因为直线与圆O相离，所以连结OM，并延长交l于P点，·=|OM|·|OP|，要使得这个乘积等于r2，取圆x2+y2=r上一点A，则|OA|=r.我们也思考这个A点在圆的什么位置？我们连结AP，发现当AP⊥OA，且OM⊥AM时，恰好符合直角三角形的射影定理，这个位置的A点即为所求.

同学：我们的作图过程如下：连结OM，过M作OM的垂线交圆x2+y2=r2于A，B两点，过A作圆O的切线交OM的延长线于P，过P且与直线OM垂直的直线即为所求.

（掌声响起）

教师：我们的同学很聪明，在直接解决问题遇到困难时，采用了由果索因的分析法来找到解题思路.类比着

②若M（x0，y0）是圆Ox2+y2=r2外一点，则直线x0x+y0y= r2与圆O：x2+y2=r2的位置关系如何？你能画出这条直线吗？

同学：同理可知，直线与圆相交，这条直线就是过M点引圆O的两条切线，切点弦所在的直线即为所求.

教师：交换了问题1的条件和结论，又生成了一个新的命题.特别是要作出满足条件的直线，借助问题1的解决思路，抓住问题共性，形成了思维“回路”.同学们在解题时，要理清解题思路，生成解题方法，优化解题过程，弄清解题通法，发现解题巧法，形成解题体系.这样学习数学，才会觉得数学越来越有味道.

二、教学反思

新的课程改革已经实施了几年，高中数学课堂教学正经历着一场重大的转型，从“知识型课堂”向“智慧型课堂”转变，老师们也在课堂教学中花了不少心思.比如制作精美的课件，补充很多现实中的例子，分小组讨论学习等等，课堂形式是丰富了，学生学的是热闹了，时间长了却发现学生感兴趣的不是数学知识，而是补充的内容.教学效果并不是很好.教学中注重生活化，注重实践都如同是做一道菜所必须的调味品一般，我们应用的合理，处理的恰到火候了才好，但是不能喧宾夺主，数学课就该体现出数学的味道.我想我们要努力的方向是做到“适合”而非“迎合”.

因为我这节课是一节解题教学课，解题教学更能发展学生思维，所以我以训练学生的思维为主脉，以问题串、知识链展开.在解题教学的每个环节，无论是解题策略的形成阶段——思路的产生和方法形成，还是在类比迁移阶段——变式拓展和方法迁移，用问题引导学生独立思考，自主探究，“思考——反思——再思——迁移”一步步推进，激发了学生学习的热情，使学生经历“不得其解时的困惑——顿悟时的激动——突破时的愉悦”的过程，从中品味到思考的乐趣，发展了思维的能力，获得了数学的思想与方法.上完这节课后，许多同学反映有一种意犹未尽、欲罢不能的“味道”.我想这种有数学味道的课堂，才能有厚重感、力量感，才能让学生长信心、长才干、长睿智.

1.黄继红.圆的切线和切点弦方程［J］.数学教学，2009（8）：34-35.Z