数学解题中无处不在的导数

☉浙江省宁海县知恩中学 何起红

数学解题中无处不在的导数

☉浙江省宁海县知恩中学 何起红

近几年高考考试中，导数的运用越来越广泛，常常与函数、不等式、数列、三角函数等结合在一起，在考查导数的单调性、值域等的同时，充分考查学生对于导数的灵活应用.很多学生因为缺少研究导数应用，常常在考试中陷入思维定势，难以解决导数问题.本文在长期的教学实践中，积极探索导数在数学解题中的运用，力争给学生的解题提供一些方向和方法，培养其较好的分析和观察能力，提升其数学能力.

一、导数在解决不等式恒成立问题中的运用

不等式恒成立问题是函数与不等式综合问题的重要内容，也是体现导数工具性的重要应用，常见方法就是结合函数转化为求函数最值，其间用到的方法是直接研究函数，或求导研究等.

例1（2015年山东高考）设函数f（x）＝ln（x+1）+a（x2-x），a∈R.

（1）讨论函数f（x）极值点的个数，并说明理由；

（2）若∀x＞0，f（x）≥0成立，求a的取值范围.

解析：（1）略.

②若a＜0，令g（x）＝2ax2+ax+1-a，Δ＝9a2-8a，此时Δ＞0，令，此时x＞0，函数2f（x）在（0，x2）上递增，在（x2，+∞）上递减，不合题意，舍去；

14≥0，则＜a≤1.

综上所述，0≤a≤1.

点评：在解决这类问题时，要使解题方法更加灵活多样，思路更加清楚和合理，就必需在解题方法上多思考、多总结，加强对这类问题的总结与反思，不断提高自身综合能力和水平，促进自身综合素质的不断提高.

二、导数在“零点不可求”问题中的运用

在导数问题中，我们经常遇到导函数的零点不能求出，但是我们可以知道导函数的零点存在且唯一，这样我们可以通过假设导函数的零点（不必求出），即“设而不求”的方法来进行推理演算，达到解题目的.这样“设而不求”在导数问题中给我们赋予新的内涵，带来启发和灵感.

例2（2012年黑龙江高考）设函数f（x）＝ex-ax-2.

（1）求函数f（x）的单调区间；

（2）若a＝1，k为整数，且当x＞0时，（x-k）f′（x）+x+1＞0，求k的最大值.

解析：（1）当a≤0时，f（x）在R上是增函数；当a＞0时，f（x）在（-∞，lna）上是减函数，在（lna，+∞）上是增函数.

（2）不等式即为（x-k）（ex-1）+x+1＞0，即对 x∈（0，+∞）恒成立.

设h（x）＝ex-x-2，x∈（0，+∞），由（1）可知，h（x）在x∈（0，+∞）上是增函数.

又h（1）＝e-3＜0，h（2）＝e2-4＞0，所以h（x）在（1，2）上有唯一的零点x0.

当x∈（0，x0）时，g′（x）＜0，g（x）在（0，x0）上是增函数；

当x∈（x0，+∞）时，g′（x）＞0，g（x）在（x0，+∞）上是减函数.

所以在（0，+∞）上，g（x）min＝g（x0）.

由h（x0）＝0，得ex0-x0-2＝0，即ex0＝x0+2，x0∈（1，2），所以

因此，k≤2，整数k的最大值为2.

点评：此例中导函数的根虽然无法求出，但是确实唯一存在，充分利用“设而不求”，设出唯一的根，变换利用导函数为零的式子.

三、导数在研究三次函数与超越函数中的运用

对于三次多项式函数及表达式中含有多项式、指数、对数等的超越函数的考查是各类考题中常涉及的热点.对于这两类函数，无法直接作出其图像，因此对于性质的研究一般要借助导数，利用导数研究这两类函数的性质或其对应方程的根的问题.

故（fx）＝（fe）＝1.又（f1）＝0，x趋向0时，（fx）＜0，x趋

maxe向+∞时，f（x）＞0.

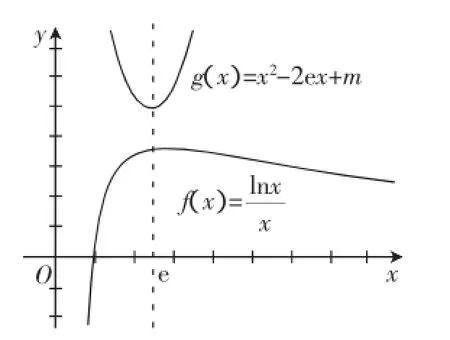
图1

由图像容易知道：

（1）当m-e2＞，即m＞e2+时，方程无解；

（2）当m-e2＝，即m＝e2+时，方程有一个根；

（3）当m-e2＜，即m＜e2+时，方程有两个根.

点评：①本题通过导数研究函数f（x）的图像形状，然后在同一坐标系中画出两个函数的图像，观察交点个数即为对应方程根的个数；②当然本题也可以令φ（x）＝f（x）-g（x），通过导数来研究φ（x）的图像，但那样较为麻烦，并且不容易进行；当然不管用哪种方法我们都要研究相应函数的图像，而对于图像，一般要借助导数来探讨出函数的单调性、极值并结合函数的其他特征来画出它的大致形状.

四、导数在一类创新题中的运用

分析近几年的高考题，由知识立意向能力立意转化，强化创新意识的考查，体现思维的发散性，注重知识的交汇，立意新颖、构思巧妙.导数的考查也从开始单纯基本知识的考查转化为综合能力的考查，题型和方法都在不断推旧出新.导数经常与不等式、新定义类题等题目一起考查.

1.导数与不等式

例4设f（x）＝lnx，g（x）＝f（x）+f′（x），证明：当0＜x＜1时，g（x）＜g（）.

点评：对于一些不等式的证明题，如果直接求解不易入手，就可以利用导数思想，通过判定函数的单调性，并由单调性判断函数的正负，使问题迎刃而解.本题利用了“构造”，应用好构造思想解题的关键是：一要有明确的方向，即以什么目的而构造；二是要弄清条件的本质特点，以便重新进行逻辑组合.

2.导数与新定义

例5（江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷）设f（x）是定义在（0，+∞）上的可导函数，且不恒为0，记（n∈ N*）.若对定义域内的每一个x，总有gn（x）＜0，则称f（x）为“n阶负函数”；若对定义域内的每一个x，总有［gn（x）］′≥0，则称f（x）为“n阶不减函数”（［gn（x）］′为函数gn（x）的导函数）.

而当a≤0时，g（1x）＝-1＜0显然在（0，+∞）上恒成立，所以a≤0.

（2）①先证f（x）≤0.

若不存在正实数x0，使得g2（x0）＞0，则g2（x）≤0恒成立，假设存在正实数x0，使得g2（x0）＞0，则有f（x0）＞0，由题意，当x＞0时，g2′（x）≥0，可得g2（x）在（0，+∞）上单调递增，当x＞x0时恒成立，即·x2恒成立，故必存在x1＞x0，使得（其中m为任意常数），这与f（x）＜c恒成立（即f（x）有上界）矛盾，故假设不成立，所以当x＞0时，g2（x）≤0，即f（x）≤0.

②再证f（x）＝0无解.

假设存在正实数x2，使得f（x2）＝0，则对于任意x3＞x2＞ 0，有，即有（fx）＞0，这与①矛盾，故假设3不成立，所以f（x）＝0无解.

综上得f（x）＜0，即g2（x）＜0.

故所有满足题设的f（x）都是“2阶负函数”.

点评：本题是新定义题，求解此类试题的关键在于寻找“类比”的对象，即将所求问题类比为所掌握的熟悉的试题类型，从而能够应用已有的思想方法进行求解.

五、导数在切线背景题中的运用

分析：本例题结构简单，清晰明了.很多学生遇到时，往往束手无策.原因之一是无法将题目条件转化为平时熟悉的模型，导致研究方向的不稳定.其实，仔细分析题中条件，过点（2，5）的直线和y＝g（x）曲线相切是一个很重要的条件.

当0＜x＜e时，Φ′（x）＜0；当x＞e时，Φ′（x）＞0.

所以Φ（x）在（0，e）上单调递减，在（e，+∞）上单调递增.

所以过点（2，5）可作两条直线与曲线y＝g（x）相切.

点评：此题需要学生对导数知识了如指掌，才能找到构造函数的基本条件，从而能轻松解决问题.

纵观近年来的高考题不难发现，利用“导数研究含有字母参数的函数的单调性、极值、最值、图像、零点等问题”的试题在高考中频频出现，而且试题的深度、广度和难度也在不断增大.试题都有一定的开发性，能有效考查学生对函数、导数、不等式和分类讨论思想方法的掌握程度、思维水平和综合能力，解题的关键是根据试题的特点，灵活运用，有时候需要多种分类融为一体，共同发挥作用.只有平时不断总结，才能提高解题能力.F