立足功能地位，突破教学难点——再谈“函数y=Asin（ωx+φ）的图像”教学

☉浙江省宁波市荣安实验中学 张润

立足功能地位，突破教学难点
——再谈“函数y=Asin（ωx+φ）的图像”教学

☉浙江省宁波市荣安实验中学 张润

众所周知，“函数y=Asin（ωx+φ）的图像”这节课的教学任务是“理解和掌握三角函数图像变换的法则”.根据教材（人教A版）的编排，本节课的教学通常都是沿袭“三步走”的教学思路.第一步：让学生动手利用“五点法”作y=Asin（ωx+φ）图像，比较y=sinx的图像，发现参数A，ω，φ在图像中所起的作用；第二步：通过例题解答，总结函数y=Asin（ωx+φ）图像变换的规律，比如，“左加右减，上加下减”的平移变换规律；第三步：从函数解析式的角度揭示图像平移、伸缩变换的一般法则，比如，平移变换“f（x）→f（x+φ）”，伸缩变换“f（x）→f（ωx）”.

我们姑且不去谈论“三步走”在操作层面上的孰是孰非，单从三角函数的功能地位——“刻画现实生活中周期现象的重要模型”来看，“三步走”的教学思路值得商榷.首先，参数“A，ω，φ”的现实意义没有得到具体体现，函数y=Asin（ωx+φ）只是作为函数y=sinx的变式而存在；其次，“周期现象的重要模型”也无从谈起，函数y= Asin（ωx+φ）只是作为研究图像变换规则的载体而已，这显然与y=Asin（ωx+φ）的功能地位相悖.由此可见，一直被广大教师所认可的“三步走”教学思路实际上是偏离了课程目标和教学主题.那具体该如何改进呢？

一、建立模型，感受函数的现实意义

相比y=sinx，用函数y=Asin（ωx+φ）来刻画“生活中的周期现象”更具一般性，它是一类“重要的数学模型”.按照教材的描述，“在物理中，简谐运动中单摆对平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系都是形如y=Asin（ωx+φ）的函数”.但遗憾的是教材（人教A版）并没有给出具体的建模过程，只是停留在“比较图像”的感性描述的层面上.这也是导致本节课教学“偏离主题”的原因之一.

（一）生活问题数学化

问题情境1：水车是我国古代发明的一种利用水力的灌溉工具，如图1，其外形酷似古代的车轮，省工、省力又省钱，现代农村还可以找到相关的实物.假定，在水流量稳定的情况下，水车上的每一个水筒都在作匀速圆周运动.我们就可以把水车抽象为如图2所示的图形，你能选择一个合适的函数模型来描述水筒（视为质点）的位置随时间的变化而变化的规律吗？

图1

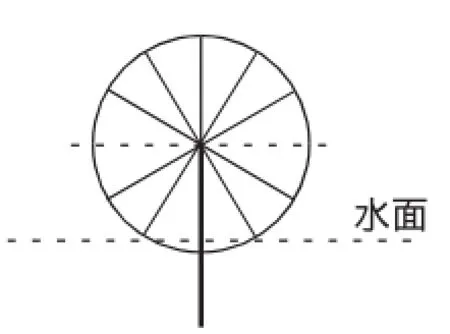
图2

水车转动最直接的效果就是导致水筒高度的变化，这也是数学建模的切入口.建模的第一步是建系，以过水车中心的直线为x轴，得到的模型会比较简洁，建立平面直角坐标系，如图3所示.

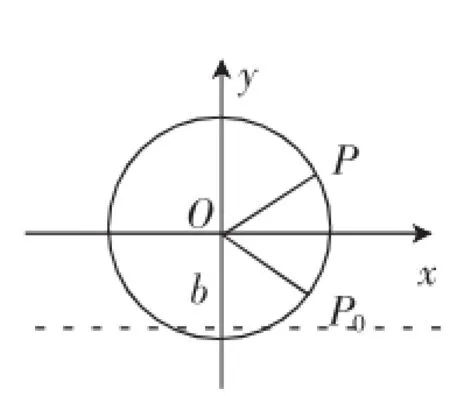
图3

（二）合理引入参数

要刻画质点高度的变化，还需要引入四个常量：水车的半径、水车中心距水面的高度，水车的旋转速度、质点的初始位置.表示这些量就需要引进相应的参数，设水车半径为R，水车中心距水面的高度为b；由于质点的高度跟水车旋转的角度有关，所以设水车转动的角速度为ω；设水车的初始位置为P0，所在半径的射线所对应的角的大小为φ.假设经过时间t后，质点运动到位置P，此时转过的角度为ωt，则质点的高度h可以表示为：h=Rsin（ωt+φ）+b，这就是刻画水筒位置随时间的变化而变化的数学模型.

教学实践表明，大部分学生能用已有的三角函数学习经验来认识水车作匀速圆周运动的问题，但对此类开放性的现实问题没有足够的实践经验，比如，如何选择坐标、如何引入参数、区分常量与变量等，这都需要教师给以有效引导，并要给充分的思考时间.经历了上述的数学建模过程，学生终于能够体会到函数y=Asin（ωx+φ）是刻画周期运动的重要模型，并且初步感受到了参数“A，ω，φ”的实际意义.

二、信息作图，探究参数对图像的影响

问题情境2：我们已经得到了水车转动的一个函数模型，根据已有经验，我们要画出它的图像，并通过图像研究性质.你觉得可以按照什么思路展开研究？

研究函数y=Asin（ωx+φ）的图像与性质，可以通过特殊到一般的思路展开，即先赋予参数“A，ω，φ”特殊值，然后再推广到一般的情况.借助几何画板软件，通过计算机模拟作图，学生可以直观地看到参数A，ω，φ对图像的影响：参数A决定图像的最高点与最低点，即振幅；参数ω决定图像的周期，即角速度；参数φ决定图像的起点，即初相.

借助信息技术研究函数图像，一是能够方便快捷地作出图像，化解了手工作图带来的困难（费时且不准确）；二是对参数进行动态赋值而实现“参数的变化对函数图像影响”的可视化；三是让学生通过自主操作，调动各种感官的作用，动静结合、手脑并用地认识匀速圆周运动中各要素对运动过程的影响，直观感知函数y= Asin（ωx+φ）的性质.这个为后面具体分析参数对图像的影响奠定了直观基础.

三、联系现实，揭示图像变换的规则

问题情境3：借助水车模型说明函数y=sin2x与y= sin（2x-）实际意义，并比较它们的异同点.

显然，这两个函数模型都是刻画半径为1，以2为角速度转动的水车上水筒高度的变化.但是，这两个水筒的起始位置不同，一个初相为0，另一个为-.

同时，借助信息技术作出这两个函数的图像，可以得到更加数学化的结论：两个函数周期相同、函数y= sin（2x-）的图像可以看成由函数y=sin2x的图像向右平移得到，这样就自然引出了本节课的重要内容——图像变换.在平时教学中，把函数y=sin2x的图像变换成函数y=sin（2x-）的图像，到底是平移还是个单位，一直是困扰学生的难点.现在，可以利用水车模型把这个问题向学生解释清楚.

由于两个水筒P，Q在同一水车作匀速圆周运动，在同一时间点上，水筒P始终与水筒Q相差弧度，也就是说，两个水筒相继经过圆上同一位置的时间差是一个定值.因为角速度为2，所以经过弧度只需用个单位时间.相应地，函数y=sin（2x-）的图像就可以看成是由函数y=sin2x图像向右平移个单位而得到.有了这个例题作铺垫，接下去就可以研究更加一般的结论.

问题情境4：借助水车模型说明函数y=sinωx与y= sin（ωx+φ）图像之间的关系.

两个水筒P，Q在单位圆上以相同的角速度ω旋转，初相差为φ，那么在转动过程中两者相继到达同一位置的时间差始终是个单位，它们的图像应该是相差个单位.

同理，也可以借助水车模型说明函数y=sinωx与y= Asinωx、函数y=Asin（ωx+φ）与y=Asin（x+φ）图像之间的关系，进而揭示图像变换的法则.如此一来，图像的平移、伸缩（横向伸缩、纵向伸缩）都可以找到对应的模型.

本课以三角函数的教学功能——“刻画现实生活中周期现象的重要模型”为切入口，创设现实问题情境，通过数学建模，不仅明确了函数y=Asin（ωx+φ）中各参数的实际意义，而且还揭示图像变换规则的实际背景，突破了教学的难点.整节课的设计依然遵循从特殊到一般、从具体到抽象的认识规律，先通过典型事例让学生观察，获得认识后再安排变式活动，最后引导学生归纳出一般结论.这显然比传统的“三步走”教学要科学合理得多.Z