一种改进的差分进化算法

丁晓阳， 李嵩华

(兰州财经大学 信息工程学院， 甘肃 兰州730020)



一种改进的差分进化算法

丁晓阳， 李嵩华

(兰州财经大学 信息工程学院， 甘肃 兰州730020)

摘要：针对基本差分进化算法收敛速度较慢的问题，将粒子群优化算法中的社会学习部分引入到差分进化算法中，提出一种改进的差分进化算法。该算法通过小概率随机变异操作增加种群的多样性和全局搜索能力；变异向量和个体向群体最优个体学习的结果进行交叉操作，利用最优个体指导进化过程，加快了算法的收敛速度，提高了优化精度。仿真实验结果表明，该算法具有更好的优化性能。

关键词:群体智能；差分进化算法；粒子群优化算法；随机变异；学习因子；多样性

MR subject classification: 68T05

差分进化算法(differential evolution，DE)是由Rainer Storn和Kenneth Price在1995年共同提出的一种采用浮点矢量编码在连续空间中进行随机搜索的优化算法[1]。DE原理简单，受控参数少，实施随机、并行、直接的全局搜索，易于理解和实现。近年来，在约束优化计算、模糊控制器优化设计、神经网络优化、滤波器设计等方面得到了广泛的应用。但是,与其他随机优化算法类似，DE仍存在着搜索停滞和早熟收敛等缺陷，因此，很多学者通过改进变异策略[2-10]、优化交叉策略[11-13]及引入其他算法的先进进化方式[14-17]对基本差分进化算法进行改进。例如，文献[2]提出一种用于求解0-1规划问题的二进制差分进化算法，该算法在进化过程中无需变异率，即可根据个体间的差异直接在离散域内进行变异。文献[3]设计了一个基于符号函数的多策略变异算子，用正负随机数代替原有的变异率，实现了两个方向上的随机搜索。文献[4]改进了差分进化算法的变异操作，采用随机选择的方式进行变异和扰动操作。文献[5]提出一种结合分阶段二次变异和混沌理论的改进差分进化算法。文献[6]提出自适应中心变异差分进化算法。文献[7]提出基于中心变异和自适应交叉概率的差分进化算法。文献[8]采用DE/rand/1和DE/best/2两种具有互补特性的差分变异算子，提出多种采用不同分配策略的新型差分变异算法。文献[9]提出一种基于新变异策略的动态自适应差分进化算法，该算法的变异策略中通过利用种群的全局最优解和目标个体的历史最优解引导种群搜索方向。文献[10]设计全局加速的变异算子，进而提出全局加速的自适应改进算法。文献[11]提出一种基于正交交叉算子的元胞差分进化算法。文献[12]将布尔逻辑运算中的异或算子引入到差分进化的变异算子中，以处理0-1整数变量，将基于正交实验设计的正交杂交算子和差分进化的杂交算子相结合，来增强差分进化算法的系统探索能力。文献[13]引进一种杂交差分进化算法，在约束条件的处理上采取动态改变惩罚力度的方法，提高了种群多样性，又保证收敛到全局最优解。文献[14]提出基于一种新的混合差分粒子群启发式优化算法的B2C电子商务物流配送优化方案。文献[15]提出一种具有人工蜂群搜索策略的差分进化算法，利用人工蜂群搜索策略对种群进行引导以帮助算法快速跳出局部最优点。文献[16]提出一种具有Pbest引导机制的适应性多策略差分进化算法，该算法设计了交叉概率控制参数库、变异尺度参数库及差分变异策略库。文献[17]提出一种基于云差分进化算法的约束多目标优化方法，通过云模型对差分进化算法的参数进行自适应处理。

以上改进算法中，缺乏对全局最优个体携带启发信息的有效利用，即由全局最优个体对其他个体的变异操作和交叉操作进行有效引导，以提高算法的有效性。为了增强DE的全局搜索能力，提高其收敛速度和优化精度，本文提出一种改进的差分进化算法(improved differential evolution，IDE)，通过对基本DE算法的变异操作和交叉操作的改进，增强了种群的多样性，同时有效利用群体最优个体的信息，提高了算法效率。最后通过仿真验证了改进的有效性。

1改进的差分进化算法

在基本的差分进化算法中，随机利用3个不同的个体进行变异和交叉，进行个体更新。这种方式较为简单，但个体的更新非常盲目，没有利用算法搜索中获得的最优个体的信息，降低了算法的效率。因此，在改进算法中，将粒子群优化算法中的社会部分引入到基本差分进化算法中，通过个体向种群最优个体Xg=(xg1，xg2，…，xgn)学习，从而使更新个体获得最优个体启发式信息，促进算法的收敛速度。

由于引入了全局最优个体这一启发式信息，随着算法的运行，个体具有向全局最优个体汇聚的趋势，从而使得个体趋同，种群多样性下降。为提高算法的全局搜索能力，通过对变异与交叉操作进行改进，增加种群的多样性和全局搜索能力。

1.1变异操作

在改进的差分进化算法中，通过对变异向量Vi进行小概率随机变异，增加种群的多样性和全局搜索能力。变异操作描述如下：

(1)

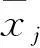
1.2交叉操作

在基本差分进化算法中，交叉操作把通过变异操作产生的变异向量Vi与父个体向量Xi进行交叉得到尝试向量Ui。在改进算法中，将粒子群优化算法中的社会学习部分引入其中，让当前个体Xi向群体最优个体Xg学习，将其结果与变异向量Vi交叉，通过利用群体最优值携带的启发式信息，提高算法的优化效率。交叉操作描述如下：

(2)

式中:CR为[0, 1]之间的常数，称为交叉常量;randj为[1,n]之间随机选择的整数;xgj为整个种群的最优个体Xg=(xg1，xg2，…，xgn)的第j维分量;c为学习因子，一般取c=2;xij+rand01×c×(xgi-xij)为社会学习部分，表示个体xi向种群最优个体Xg学习。图1为改进算法交叉操作示意图。

图1　改进算法交叉操作示意图

1.3选择操作

选择操作同基本差分进化算法。差分进化算法通过变异算子和交叉算子产生子群体之后，采用一对一选择算子将子个体与相应的父个体进行比较，较优个体保存到下一代群体中。选择操作可描述如下：

(3)

其中，f(Xi)为个体Xi的适应值。由于差分进化算法采用的是一对一竞标赛选择，因此该算法可以保证精英解(elitism)在进化过程中不会丢失。

1.4改进算法的流程图

流程图如图2所示。

图2　改进差分进化算法流程图

2仿真实验

2.1实验设计

分别用基本的差分进化算法DE1和本文提出的IDE求以下8个基准测试函数的最小值，进行对比实验，以评价改进算法的优化性能。

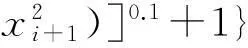
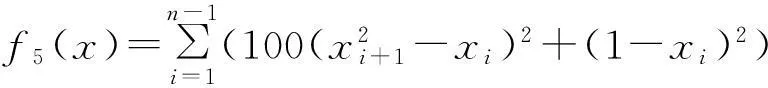
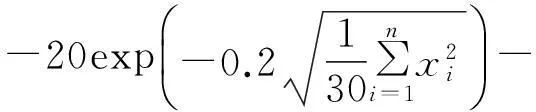
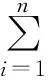
其中

yi=1+0.25(xi+1);n=30;

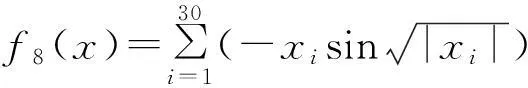
实验中，DE1与IDE的种群规模都设为50，并取F=0.5，CR=0.3，Pr=0.02(对f4函数取Pr=0.05)，c=2。各函数相关的实验参数如表1所示。

表1　用于测试改进算法的基准函数参数表

算法的性能评估采用如下方法：固定进化迭代次数，对每个函数的不同维独立运行30次，记录它们的平均最优值和标准差，以评估改进算法的性能。

2.2 实验结果及分析

表2为30次实验所得的两个算法求解不同维数的8个函数所得的平均值和标准差。可以看出，IDE对于3种不同维数的f1、f2、f5、f6、f7、f8函数以及20维和30维的f4函数求解的平均最优值都要优于DE，且标准差也更小(10维的f5函数和100维的f6函数IDE的标准差虽略逊于DE，但相差不多)；对于3种不同维数的f3函数以及10维的f4函数，用IDE求解的平均值和标准差，都要比DE差。这说明，总体上改进的差分进化算法求解精度较高，且较为稳定，要比基本的差分进化算法有更大的优越性。

表2　两种算法的实验结果

图3—10列出了函数f1—f8采用两种算法在求解实验所选取的各个函数的最高维时运行30次后得到的平均极值进化曲线，在图3—9中，纵坐标用函数平均极值的常用对数表示，在图10中，因f8函数的极值为负，纵坐标直接用函数的平均极值表示，各图中横坐标均为迭代次数。当函数值为0时，则对函数值均加上10-11作为截止值。从图中可以看出，除100维的f3函数外，IDE对于其余列出的7个函数都能比DE更快速地收敛于更好的解，这说明，改进的差分进化算法收敛速度较快且优化精度较高。

图3　100维的f1函数平均极值的进化曲线

图4 30维的f2函数平均极值的进化曲线

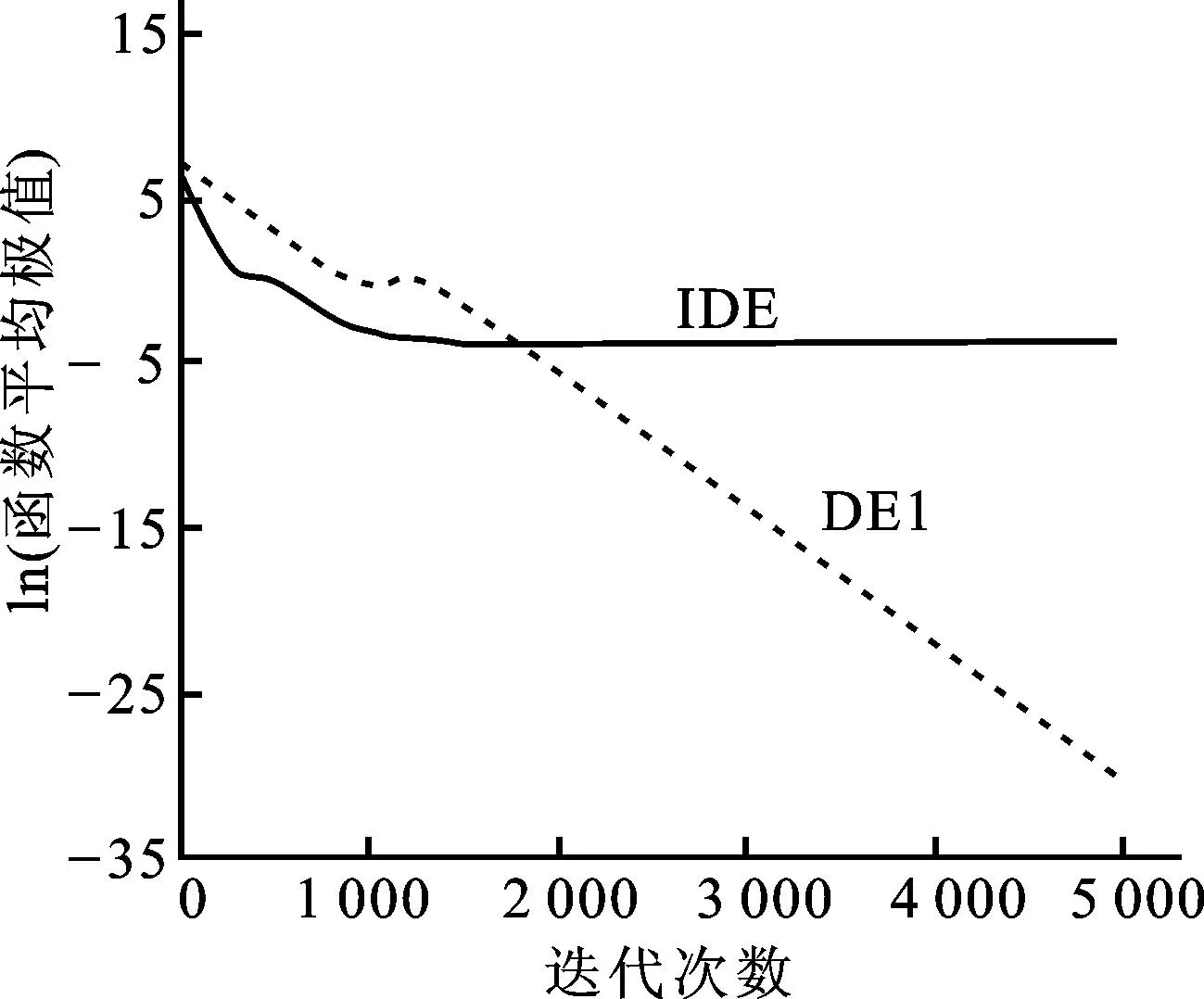
图5　100维的f3函数平均极值的进化曲线

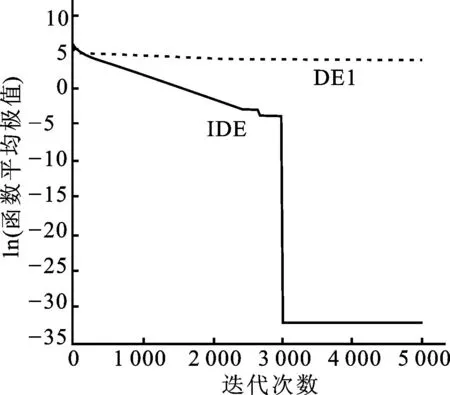
图6 30维的f4函数平均极值的进化曲线

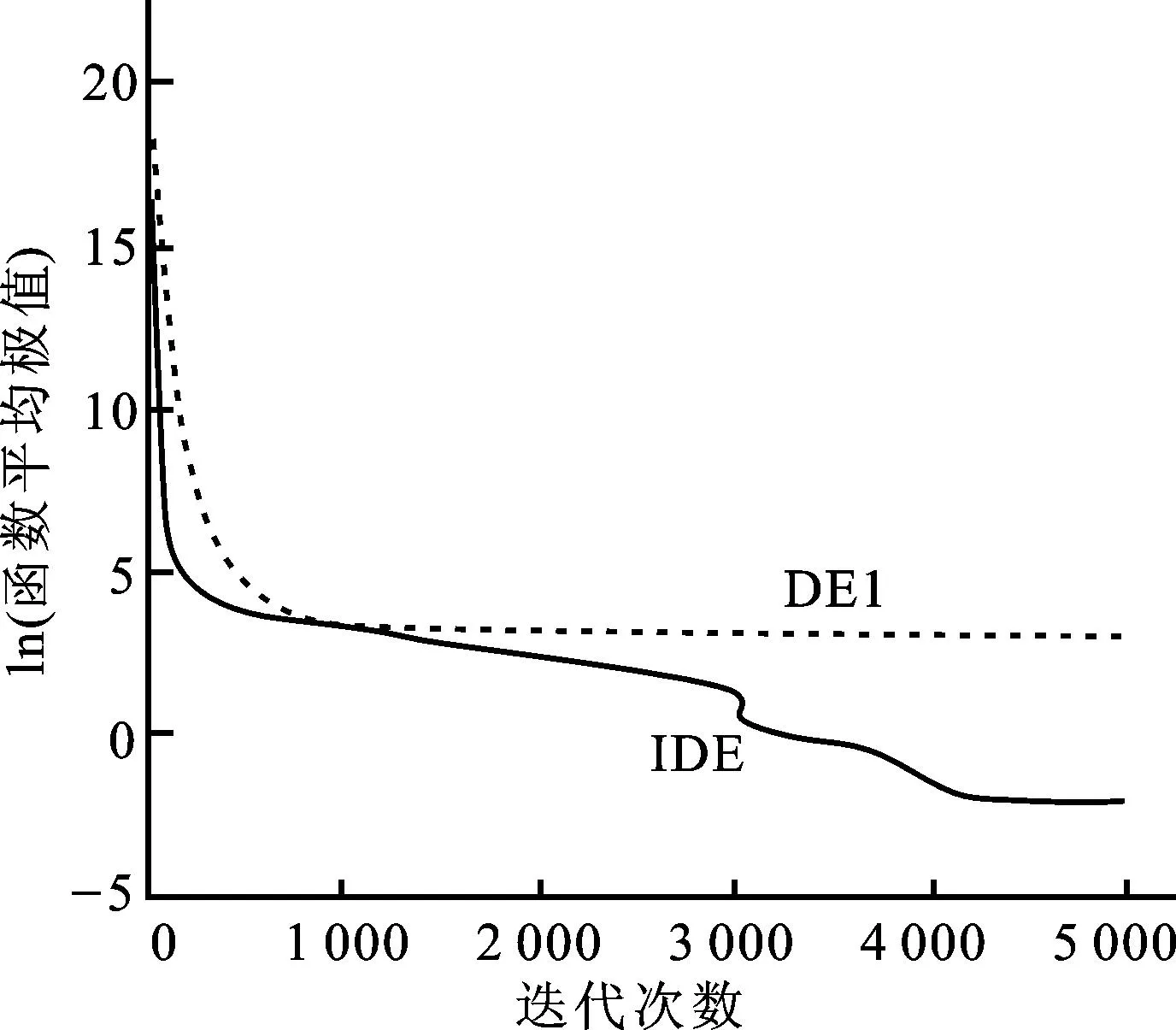
图7　30维的f5函数平均极值的进化曲线

图8 100维的f6函数平均极值的进化曲线

图9100维的f7函数平均极值的进化曲线

Fig.9Evolution curve of average extremes with

functionf7of dimension 100

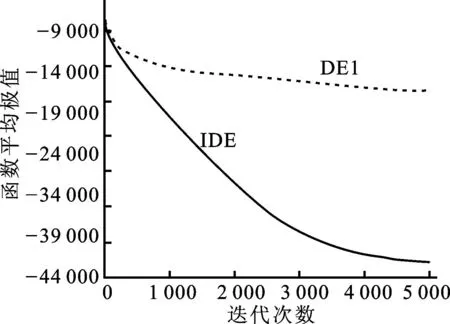
图10 100维的f8函数平均极值的进化曲线

3结论

为了提高基本DE算法的搜索效率，对基本差分进化算法进行了改进，提出了一种改进的差分进化算法。该算法在变异操作中通过以小概率引入随机个体，增加了种群的多样性。同时，针对新产生的个体，在交叉操作中增加了全局最优个体的启发式信息，以促进算法的收敛。最后，通过对8个benchmark函数的仿真实验，对算法进行了验证。

参考文献:

[1] STORN R, PRICE K. Differential evolution:a simple and efficient adaptive scheme for global optimization over continuous spaces[R].Berkley: International Computer Science Institute，1995.

[2] 孔祥勇,高立群,欧阳海滨,等. 无参数变异的二进制差分进化算法[J]. 东北大学学报(自然科学版),2014,35(4):484-488.

[3] 孔祥勇,高立群,欧阳海滨,等. 双向随机多策略变异的自适应差分进化算法[J]. 计算机集成制造系统,2014,20(8):1948-1958.

[4] 欧阳海滨,高立群,孔祥勇. 随机变异差分进化算法[J]. 东北大学学报(自然科学版),2013,34(3):330-334.

[5] 王筱珍,李鹏,俞国燕. 分阶段二次变异的多目标混沌差分进化算法[J]. 控制与决策,2011,26(3):457-463.

[6] 池元成,方杰,饶大林,等. 自适应中心变异差分进化算法及其在涡轮叶型优化设计中的应用[J]. 航空动力学报,2010,25(8):1849-1854.

[7] 池元成,方杰,蔡国飙. 中心变异差分进化算法[J]. 系统工程与电子技术,2010,32(5):1105-1108.

[8] 辛斌,陈杰,彭志红,等. 基于互补变异算子的自适应差分进化算法[J]. 东南大学学报(自然科学版),2009,39(s1):10-15.

[9] 毕晓君,刘国安,肖婧. 基于新变异策略的动态自适应差分进化算法[J]. 计算机研究与发展,2012,49(6):1288-1297.

[10] 孔祥勇,高立群,欧阳海滨,等. 求解大规模可靠性问题的改进差分进化算法[J]. 东北大学学报(自然科学版),2014,35(3):328-332.

[11] 丁青锋,郑国莘,杨柳. 基于反学习和正交交叉算子的元胞差分进化算法[J]. 北京邮电大学学报,2014,37(3):7-12.

[12] 张莉,李宏,冯大政. 求解混合整数规划的嵌入正交杂交的差分进化算法[J]. 系统工程与电子技术,2011,33(9):2126-2132.

[13] 初飞雪,吴长春. 成品油管道杂交差分进化法优化设计[J]. 哈尔滨工业大学学报,2009,41(5):241-244.

[14] 沈济南,梁芳,郑明辉. 一种新的混合差分粒子群优化算法及其应用[J]. 四川大学学报(工程科学版),2014,46(6):38-43.

[15] 黄玲玲,刘三阳,高卫峰. 具有人工蜂群搜索策略的差分进化算法[J]. 控制与决策,2012,27(11):1644-1648.

[16] 向万里,马寿峰,安美清. 具有Pbest引导机制的适应性多策略差分进化算法[J]. 模式识别与人工智能,2013,26(8):711-721.

[17] 毕晓君,刘国安. 基于云差分进化算法的约束多目标优化实现[J]. 哈尔滨工程大学学报,2012,33(8):1022-1031.

〔责任编辑宋轶文〕

第一作者： 段景瑶,女,博士研究生,主要研究方向为不确定性推理。E-mail:nancy-duan@163.com

An improved differential evolution algorithm

DING Xiaoyang, LI Songhua

(School of Information Engineering, Lanzhou University of Finance

and Economics, Lanzhou 730020, Gansu, China)

Abstract:In order to enhance the convergence rate of differential evolution algorithm (DE),an improved differential evolution algorithm (IDE) is proposed which introduced the social learning part of particle swarm optimization algorithm into itself. Firstly, the new algorithm improves the diversity of population and global searching ability by small probability random mutation operator. Then, the variation vector and the result which learns from the best individual in population are crossed. The evolutionary process is guided by best individual so that the convergence rate and the optimization precision of DE are improved.The simulation results show that the improved algorithm has better optimization performance.

Keywords:swarm intelligence; differential evolution algorithm; particle swarm optimization; random mutation; learning factor; diversity

基金项目：国家自然科学基金(11171200,11271237,61228350,6100546); 陕西省教育厅专项科研计划(14JK1050); 宝鸡文理学院院级重点项目(ZK14059)

收稿日期：2015-03-15

doi:10.15983/j.cnki.jsnu.2016.01.112

文章编号：1672-4291(2016)01-0007-07

中图分类号：TP181

文献标志码：A