夹角型纵振变幅杆的有限元设计

张海岛, 贺西平

(陕西师范大学 物理学与信息技术学院， 陕西 西安 710119)



夹角型纵振变幅杆的有限元设计

张海岛, 贺西平*

(陕西师范大学 物理学与信息技术学院， 陕西 西安 710119)

摘要：对夹角型纵振动变幅杆进行了有限元设计,计算了不同尺寸变幅杆纵振动谐振状态下的放大系数与纵振动位移分布。结果显示：放大系数主要受变幅杆输入杆与输出杆的长度及半径的影响,输入杆与输出杆间的夹角对放大系数影响不大。而纵振动位移分布与节点位置则受角度影响较大。加工了5个不同尺寸变幅杆并利用激光测振仪测量其振型与纵振动放大系数,测试显示纵振动可由输入端传递至输出端上,放大系数测试结果与有限元计算一致。

关键词:夹角；变幅杆；有限元；放大系数；位移分布

PACS: 43.38.+n

超声变幅杆以增加机械波能量密度的方式实现超声振动的放大,是超声振动系统的关键部件,在焊接、制造、切割、打孔等技术领域具有广泛的应用[1]。变幅杆在超声振动系统中起振幅放大和阻抗匹配的作用,因此变幅杆研究对提高超声振动系统性能有重要意义。文献[2-3]不仅对传统超声变幅杆,如圆锥型、指数型、悬链线型与阶梯型等进行了研究,还对近年新型的变幅杆进行了讨论。文献[4-5]将遗传算法与有限元结合,分别提出了贝塞尔曲线型变幅杆与B样条曲线型变幅杆,两种变幅杆与同尺寸悬链线型变幅杆相比其振幅比有较大提高。文献[6-7]利用变分原理,分别设计了放大系数为5、位移节点位于不同位置的变幅杆的形状。

变幅杆的设计方法也是研究人员关注的对象。常见的方法有传统解析法[8]、等效电路法、替代法、传输矩阵法、有限元法等[9]。文献[10]发现常见变幅杆的节点与应变极大点位置之和等于变幅杆一阶振型的谐振长度，这一结论有助于简化设计过程。

在纵振动超声技术中,换能器连接变幅杆,能量沿直线方向传播。实际应用中，往往需要改变纵振动传输方向,如弯曲管子内表面的清洗等问题。为此本文提出了一种新型的夹角型变幅杆，并对该型纵振变幅杆进行了有限元设计。计算了该型变幅杆纵振动谐振状态下的振型、放大系数与位移分布,研究了放大系数及位移分布与变幅杆尺寸的关系。利用激光测振仪实验测试了变幅杆的振型与放大系数。

1有限元设计及计算

夹角型纵振动变幅杆如图1所示,建立变幅杆有限元模型,变幅杆由输入杆Ⅰ杆与输出杆Ⅱ杆组成, Ⅰ杆轴线与x轴重合,原点位于两杆中心轴线的连接处,l、r为杆的长度和半径,θ为两杆间的夹角。ε为杆轴线上各点的纵振动位移,Ux、Uy为杆轴线上各点沿x轴、y轴方向的位移,下标1、2分别代表Ⅰ杆、Ⅱ杆中的变量。

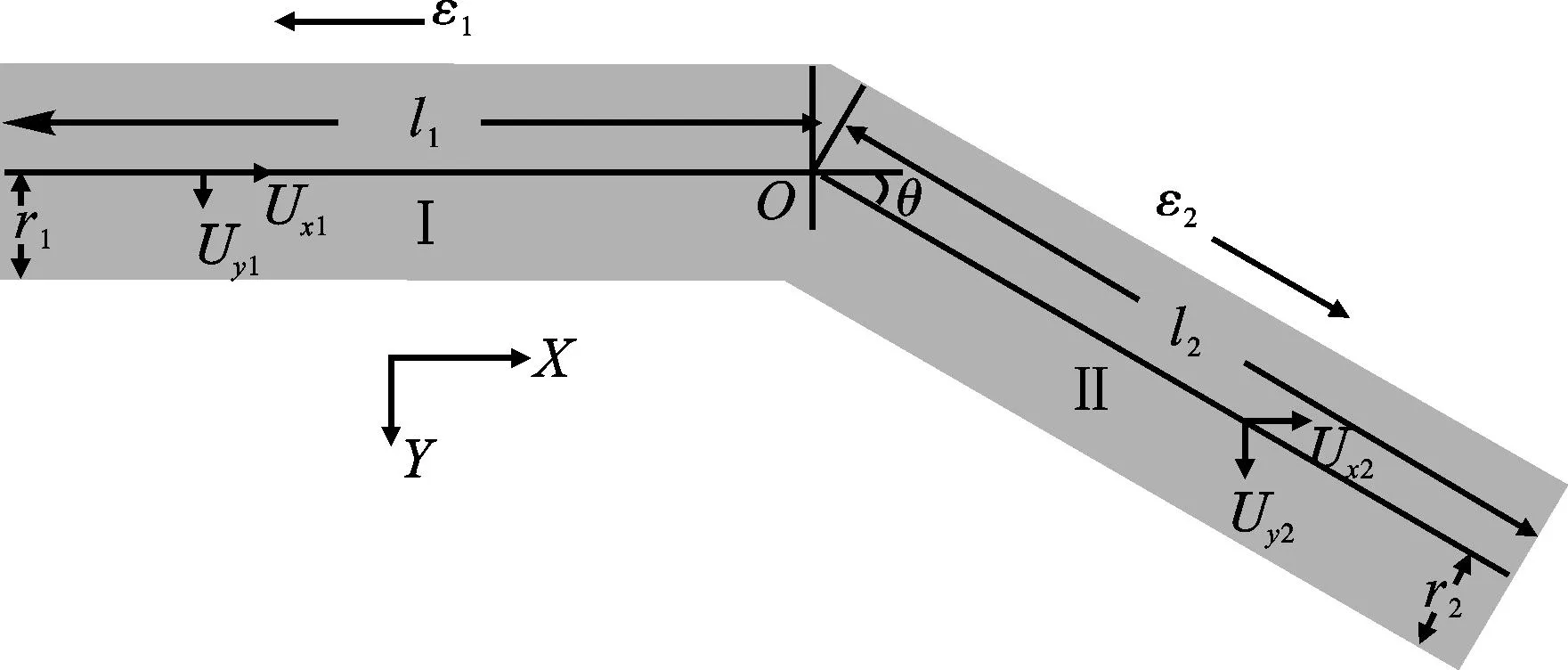
图1　夹角型纵振动变幅杆

1.1 纵振振型与放大系数

取材料为45#钢,其杨氏模量E=210×109N/m2,泊松比σ=0.269,密度ρ=7 800 kg/m3。有限元计算了表1中10种尺寸的变幅杆，图2示出了1#变幅杆的振型。

表1　变幅杆有限元计算结果*

*.fe为纵振动谐振频率,Me为放大系数的计算值。

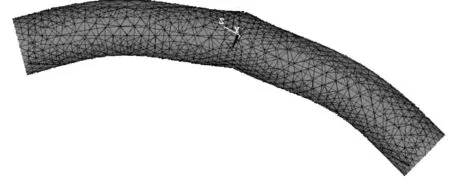
图2　1#变幅杆纵振动振型

1.2纵振动位移分布

有限元计算得到变幅杆在纵振谐振状态下轴线上各点沿坐标轴方向的位移Ux、Uy，利用以下两式可得到变幅杆沿轴线各点的纵振动位移:

ε1=Ux1,

(1)

ε2=Ux2cosθ+Uy2sinθ。

(2)

图3即为上式计算得到的1#杆的归一化纵振动位移分布曲线。

图3 1#变幅杆位移分布

通过有限元计算结果可知, 在两杆连接处沿坐标轴x、y方向的位移是连续的,即在原点处有

Ux1=Ux2,Uy1=Uy2。

但因为有夹角，式(1)、(2)计算得到的沿轴向方向上的纵振动位移在原点处不连续,即ε1≠ε2。计算表明，输出杆与输入杆尺寸相同时, 该纵振动位移在原点不连续的程度随两杆间夹角的增大而增大；当两杆间夹角不变,输出杆半径比输入杆小时,位移不连续的程度随输出杆半径的减小而增大；当两杆间夹角不变,输出杆长度比输入杆小时, 位移不连续的程度将减小。

2实验及讨论

加工了表1中的1#、4#、5#、6#和7#变幅杆。 与变幅杆相连的纵振动换能器工作频率为19.8 kHz。利用Polytec PSV-400扫描式激光测振仪测试换能器与变幅杆组成的振动系统,对变幅杆端面振动分布与放大系数进行了测量。放大系数测试结果如表2所示,表中下标e为有限元计算值,t为实验测试值,有限元计算频率与实验测试值的误差为Δ1=|(fe-ft)/ft|,误差值为4.39%~15.99%。有限元方法计算放大比与实验测试值的误差为Δ2=|(fe-ft)/ft|,误差值为0.47%~5.6%。有限元计算与实验测试结果一致。1#变幅杆输出端面振动分布如图4所示。图上半部分为变幅杆输出端面振动位移测试结果，下半部分为位移频率响应，其中标亮部分为振动系统纵振振型对应的频率。根据测试结果可知,在频率ft=19 953 Hz处纵振动经过变幅杆成功地传递到变幅杆输出端。

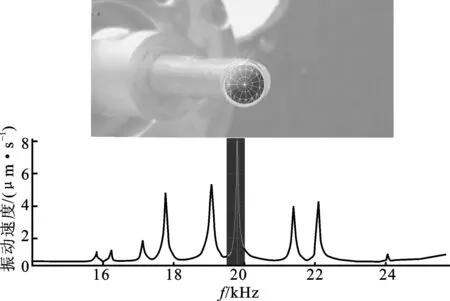
图4　1#变幅杆纵振振型,ft=19 953 Hz

根据表1所示的计算结果,变幅杆的纵振放大系数与输入杆及输出杆的相对尺寸相关。输入杆与输出杆尺寸相同时,放大系数为1,与两杆间夹角无关,如1#、4#与7#。输入杆与输出杆半径相同,当输出杆长度小于输入杆时,放大系数小于1,并且放大系数随角度的增大略微减小,如2#、5#与8#。当输出杆长度大于输入杆时,放大系数大于1,如10#；当输入杆半径大于输出杆半径时,变幅杆能起到振动放大作用,如3#、6#与9#，所以变幅杆的纵振放大系数与两杆的相对尺寸密切相关。

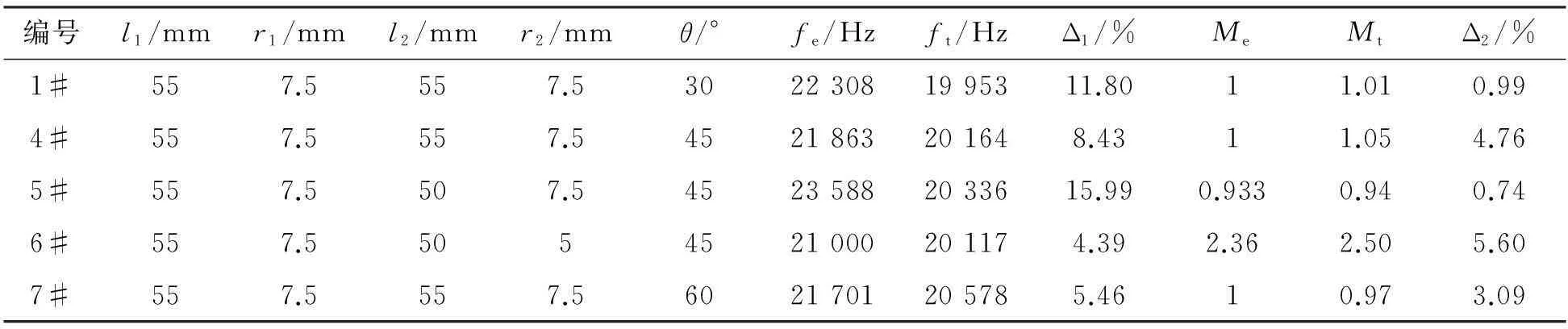
表2　变幅杆实验测试结果

进一步测试了激励电压与各变幅杆输出端位移与放大系数的关系。图5为1#变幅杆输出位移与激励电压关系图。可以看出,输出位移随电压增大基本呈线性增加。各变幅杆放大系数与激励电压关系如图6所示,结果显示放大系数随电压的增大基本保持不变。 测试表明变幅杆具有较好的线性输出特征。

图5　1#变幅杆输出位移与电压的变化关系

图6　不同变幅杆放大系数与电压的变化关系

3 结论

本文对夹角型纵振变幅杆进行了有限元设计,研究了纵振动放大系数及位移分布与变幅杆尺寸的关系,得到如下结论：

(1) 提出了夹角型纵振变幅杆并进行了有限元设计,实验测试表明变幅杆为纵振振型。

(2) 两杆的长度与半径是影响放大系数的主要因素,放大系数随输入杆长度减小或半径增大而增大,两杆间夹角对其影响较小。

(3) 变幅杆放大系数的有限元计算值与实验测试值基本一致。

(4) 在变幅杆的输入杆与输出杆的连接处纵振动位移不连续,不连续的程度随夹角的增大而增大,随输入杆长度的减小或输出杆半径的减小而增大。

(5) 测试输出位移及放大系数与激励电压的关系表明,变幅杆具有较好的线性输出特征。

参考文献：

[1] 林仲茂. 超声变幅杆的原理和设计[M]. 北京：科学出版社,1987.

[2] 贺西平,程存弟.几种常见形状函数超声变幅杆性能参量的统一表达[J]．陕西师范大学学报(自然科学版),1994,22(3):29-32.

[3] 汪彦军,贺西平,张频.超声变幅杆性能参数的计算机辅助设计[J]．应用声学,2007,26(3):181-184.

[4] WANG D A, CHUANG W Y, HSU K, et al. Design of a B zier-profile horn for high displacement amplification[J]. Ultrasonics, 2011,51(2):148-156.

[5] HUU T N, HAI D N,JUN Y U, et al. A nonrational B-spline profiled horn with high displacement amplification for ultrasonic welding[J]. Ultrasonics, 2014,54(8):2063-2071.

[6] IOAN C R, SERGIU T C, NICOLAE C C. Ultrasonic horns optimization[J]. Physics Procedia, 2010, 3(1):1033-1040.

[7] IOAN C R,MIHAIL I P, NICOLAE C. Experimental and numerical study on an ultrasonic horn with shape designed with an optimization algorithm[J].Applied Acoustics, 2015,95:60-69.

[8] ARTHUR G W. Acoustical impedance and the theory of horns and the phonograph[J].Proceedings of the National Academy of Sciences of the United States of America, 1919, 5(7):275-282.

[9] 贺西平, 高洁. 超声变幅杆设计方法研究[J]. 声学技术, 2006,25:82-86.

[10] 刘豆豆,贺西平,李家星.变幅杆位移节点和应变极大位置的关系[J].陕西师范大学学报(自然科学版), 2014,42(3): 48-51.

〔责任编辑 李博〕

第一作者： 乔晓阳，女，硕士研究生，研究方向为功率超声。E-mail:1207162657@qq.com

Design of angled longitudinal horn with finite element method

ZHANG Haidao, HE Xiping*

(School of Physics and Information Technology, Shaanxi Normal University,

Xi′an 710119, Shaanxi, China)

Abstract:A angled longitudinal horn is investigated through finite element method. The amplification factors and displacement distributions of the horns are calculated at their resonant frequency of longitudinal vibration. The calculated results show that amplification factor is mainly influenced by the length and radius of the horn, whereas the angle of the horn plays a little role. The longitudinal displacement is mainly depended on the angle of the horn. 5 different angled horns are manufactured and their vibration modes and amplification factors are measured by experiment with Polytec scanning vibrometer. It shows that the longitudinal vibration is successfully transferred to the output ports via the angled horn and the text values of amplification factors are compared with the finite elemental results.

Keywords:angle; solid horn; finite element method; amplification factor; displacement distribution

通信作者：* 林书玉，男，教授，博士生导师。E-mail:sylin@snnu.edu.cn.

基金项目：国家自然科学基金(11174192,11374200,11474192)

收稿日期：2015-01-29

doi:10.15983/j.cnki.jsnu.2016.01.215

文章编号：1672-4291(2016)01-0043-06

中图分类号:O426.2

文献标志码:A