新型夹心式压电陶瓷复合变压器的特性

乔晓阳, 林书玉

(陕西师范大学 物理学与信息技术学院，陕西省超声重点实验室，陕西 西安 710119)



新型夹心式压电陶瓷复合变压器的特性

乔晓阳, 林书玉*

(陕西师范大学 物理学与信息技术学院，陕西省超声重点实验室，陕西 西安 710119)

摘要：提出一种新型多层复合夹心式纵向极化压电陶瓷变压器,并应用等效电路方法对压电振子的机电特性进行分析，推导出输入电阻、共振频率、反共振频率和电压增益的解析解，得出并分析了变压器第一、第二共振与反共振频率、机电耦合系数及电压增益与变压器的长度、负载电阻的关系。研究表明，一阶机电耦合系数在特定尺寸上和特定负载上均有最大值；一阶电压增益只在特定尺寸上存在最大值。将计算所得的共振频率、反共振频率与ANSYS模拟结果及实验测量结果进行比较验证，模拟结果及实验测量结果和理论计算值吻合。

关键词:压电变压器; 纵向振动; 等效电路; 共振; 电压增益

PACS: 43.35.+d

压电陶瓷变压器因其体积小、质量轻、高功率密度、高效率、避免电磁干扰而且不存在漏磁现象对环境造成污染等特点，受到了越来越多的关注，在诸多领域特别是电子技术领域，呈现出取代传统大体积磁芯变压器的趋势[1-5]。压电陶瓷变压器通过在输入端利用逆压电效应将电能转化成机械能，在输出端利用压电效应将机械能转化为电能来实现变压。压电变压器工作时，其振动模式有：纵向振动模式、厚度振动模式、径向振动模式和弯曲振动模式。每种振动模式在实际应用中都有着各自的优势[2-11]。

传统的厚度振动模式压电陶瓷变压器利用两片或多片厚度方向极化的压电陶瓷圆盘，通过改变压电陶瓷圆盘的厚度来实现电压的改变。由于压电陶瓷材料的导热性能不佳，导致此类压电陶瓷变压器在比较大功率下工作时发热较为严重，因此传统的厚度振动模式压电陶瓷变压器不适合在大功率状态下工作。本文提出了新型夹心式压电陶瓷变压器，它由前后金属盖板、中间金属块及两组厚度极化的压电陶瓷片共轴连接而成。由于使用了金属材料，其导热性能大大改善，解决了压电陶瓷在大功率状态下易发热、能量转换效率下降的问题。利用等效电路法对这种变压器的纵向振动进行了分析，研究了金属块不同长度比及不同负载电阻下压电陶瓷变压器的共振频率、反共振频率、电压增益和有效机电耦合系数的变化规律，为进一步优化该变压器提供了一定的理论依据。

1夹心式压电陶瓷变压器等效电路

新型夹心式压电陶瓷变压器结构如图1所示，由三节长度分别为l1、l2、l3的金属棒和两组厚度分别为l01、l02的压电陶瓷片组成。第一组压电片加电压E,第二组压电片加负载R。整个棒半径为R0。由于变压器横向尺寸远小于纵波波长，所以本文中只考虑变压器的纵向振动[12-13]。

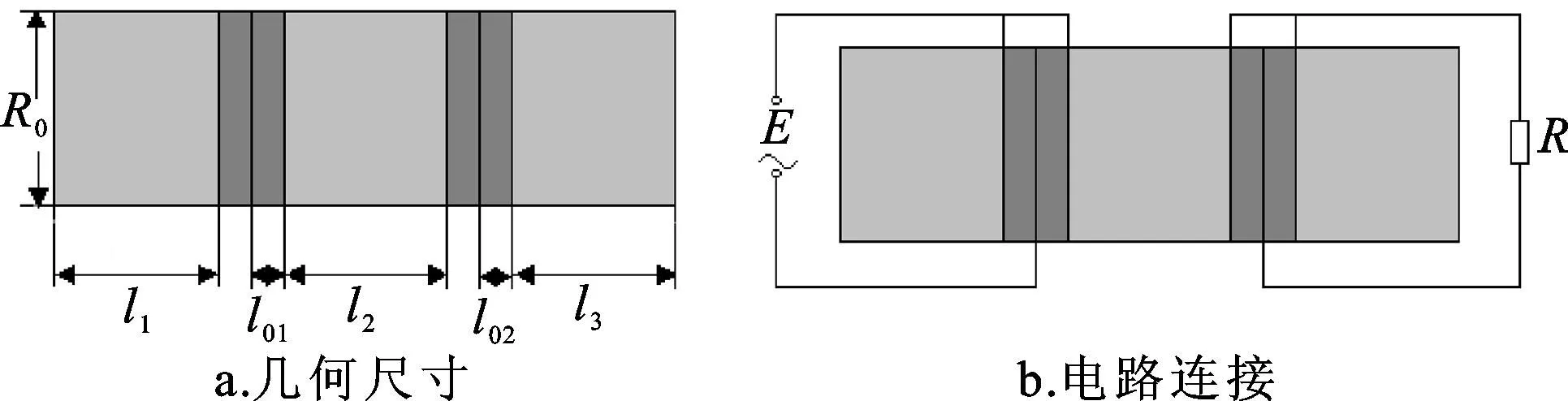
图1　夹心式压电陶瓷复合变压器

变压器等效电路如图2所示，第一组压电片加激励电压，第二组压电片加负载电阻。其中C1、C2和n1、n2分别为两组压电陶瓷的静态电容和机电耦合系数。其表达式为:

(1)

(2)

(3)

(4)

图2　夹心式压电陶瓷复合变压器的机电等效电路

图2中Z11、Z12、Z13，Z21、Z22、Z23，Z31、Z32、Z33分别为金属前盖板，中间金属块，金属后盖板在等效电路中的串并联阻抗。表达式为:

Z11=Z12=jZ1tan(k1l1/2);

(5)

Z13=Z1/[jsin(k1l1)];

(6)

Z21=Z22=jZ2tan(k2l2/2);

(7)

Z23=Z2/[jsin(k2l2)];

(8)

Z31=Z32=jZ3tan(k3l3/2);

(9)

Z33=Z3/[jsin(k3l3)]。

(10)

其中:Z1=ρ1c1S,Z2=ρ2c2S,Z3=ρ3c3S;k1=ω/c1,k2=ω/c2,k3=ω/c3;c1=(E1/ρ1)1/2,c2=(E2/ρ2)1/2,c3=(E3/ρ3)1/2;E1、E2、E3,ρ1、ρ2、ρ3,c1、c2、c3分别为金属材料的杨氏模量，密度和声波在其中传播时的声速,k1、k2、k3为波数,ω=2πf为角频率。Zp11、Zp12、Zp13和Zp21、Zp22、Zp23分别为两组压电陶瓷片在等效电路中的串并联阻抗，其表达式如下：

Zp11=Zp12=jZ01tan(p1k01l01/2);

(11)

Zp13=Z01/[jsin(p1k01l01)];

(12)

Zp21=Zp22=jZ02tan(p2k02l02/2);

(13)

Zp23=Z02/[jsin(p2k02l02)]。

(14)

其中:Z01=ρ01c01S,Z02=ρ02c02S;k01=ω/c01,k02=ω/c02;c01=(E01/ρ01)1/2,c02=(E02/ρ02)1/2;E01、E02,ρ01、ρ02,c01、c02分别为两组压电陶瓷片的杨氏模量，密度和声波在其中传播时的声速,k01、k02为波数,ω=2πf为角频率。

当变压器前后机械自由时，由等效电路可得金属前后盖板的阻抗为:

Zm1=jZ1tan(k1l1)=jD;

(15)

Zm3=jZ3tan(k3l3)=jA。

(16)

2变压器的共振频率方程和电压增益

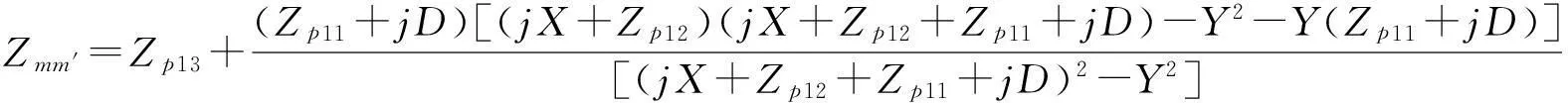
(17)

(18)

(19)

(20)

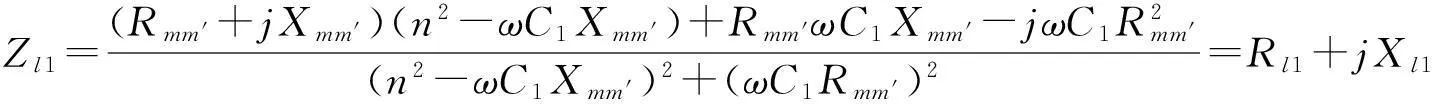
(21)

其中,C为第二组压电片和金属后盖板的总阻抗，B为中间金属块、第二组压电片和金属后盖板的总阻抗,F为简化计算引入的中间参量。

根据上式，当Zl1= 0时,可得压电陶瓷变压器的共振频率方程为

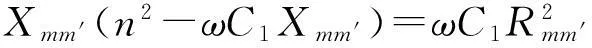
(22)

当Zl1为无穷大时，可得反共振频率方程为

(n2-ωC1Xmm′)2+(ωC1Rmm′)2=0。

(23)

由图2可得，变压器的电压增益V2/V1如下式所示

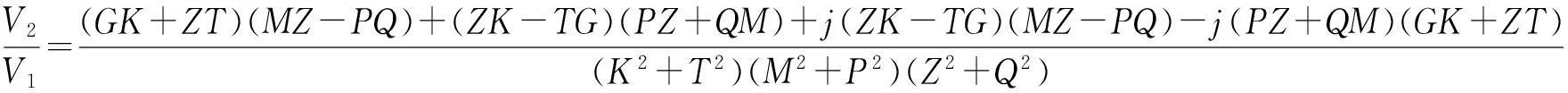
(24)

其中,X、Y、V、W、Z、G、K、T、H、Q、M、P为简化计算引入的中间参量,X、Y、V、W由(18)、(19)式给出，Z、G、K、T、H、Q、M、P表达式如下：

Z=Z23F{(Zp11Zp22-DA)[(VX-WY)

(-RωC1)+WX+VY]+(AZp11+DZp22)[(WX+VY)RωC1+(VX-WY)]};

(25)

G=Z23F{(Zp11Zp22-DA)[(WX+VY)RωC1+(VX-WY)]-(AZp11+DZp22)[(VX-WY)(-RωC1)+WX+VY]};

(26)

K=-Zp13(Z21+Zp11)-Zp11Z21+

DXY(ZP13+Zp11);

(27)

T=-Zp13(X+D)-DZ21-Zp11X)+YD;

(28)

H=-Zp12(Z22+Z23)-Z23Z22+

W(Z23+Zp23);

(29)

Q=-(Zp12+Z22)V;

(30)

M=-Zp21(Zp22+Zp23)-Zp22Zp23-AFRωC1+F(Zp21+Zp22);

(31)

P=-Zp21(A-FRωC1)-AZp23+

Zp22FRωC1+FA。

(32)

而有效机电耦合系数keff可由下式得出:

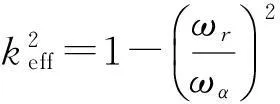
(33)

其中,ωr=2πfr,ωa=2πfa，fr和fa分别为变压器的共振与反共振频率。

3变压器共振频率、有效机电耦合系数和电压增益的特性分析

改变压电陶瓷材料的厚度和形状、前后金属盖板的几何尺寸和形状以及负载电阻就可以改变变压器的共振频率、有效机电耦合系数和电压增益。本节将从两方面对变压器各项参数进行特性分析。公式中出现的材料参数为：ρ1=ρ2=ρ3=2 700 kg/m3,ρ01=ρ02=7 500kg/m3，其他参数和物理系数见表1。

表1　夹心式压电陶瓷复合变压器设计中使用的材料参数

3.1负载无穷大时几何尺寸对变压器性能的影响

固定金属前盖板长度l1和变压器总长度l2+l3的值，改变l2，令l2=0.04-l3，R=100 Ω，带入公式(22)、(23)、(33)、(24)中，即可得出此时的共振频率、反共振频率、有效机电耦合系数以及电压增益与l2的关系，分别如图3、4、5所示。

图3　压电变压器的共振及反共振频率与l2的关系

图4　机电耦合系数与l2的关系

图5　电压增益与l2的关系

由图3可以看出, 压电变压器一阶模态下的共振、反共振频率随着中间金属长度l2的增大而减小。二阶模态下的共振频率在l2=0.024 m，l3=0.016 m附近达到最大，反共振频率在l2=0.027 m，l3=0.013 m附近达到最大。

由图4可以看出,在l2=0.015 m，l3=0.035 m附近，压电变压器一阶模态下的有效机电耦合系数有最大值；在l2=0.017 m，l3=0.033 m附近，二阶模态下的有效机电耦合系数有最小值。

由图5可以看出，变压器在一阶共振模态下的电压增益随着l2的增大先减小后在l2=0.01 m后变化缓慢；在l2=0.017 m，l3=0.033 m处，二阶共振模态下的电压增益达到最大值。

3.2负载对压电陶瓷变压器机电特性的影响研究

令l1=l2=l3=0.02 m，改变式(22)、(23)、(33)、(24)中负载电阻R的数值，可得出变压器各部分尺寸固定时的共振频率、反共振频率、有效机电耦合系数以及电压增益与负载电阻的关系，分别如图6、7、8所示。

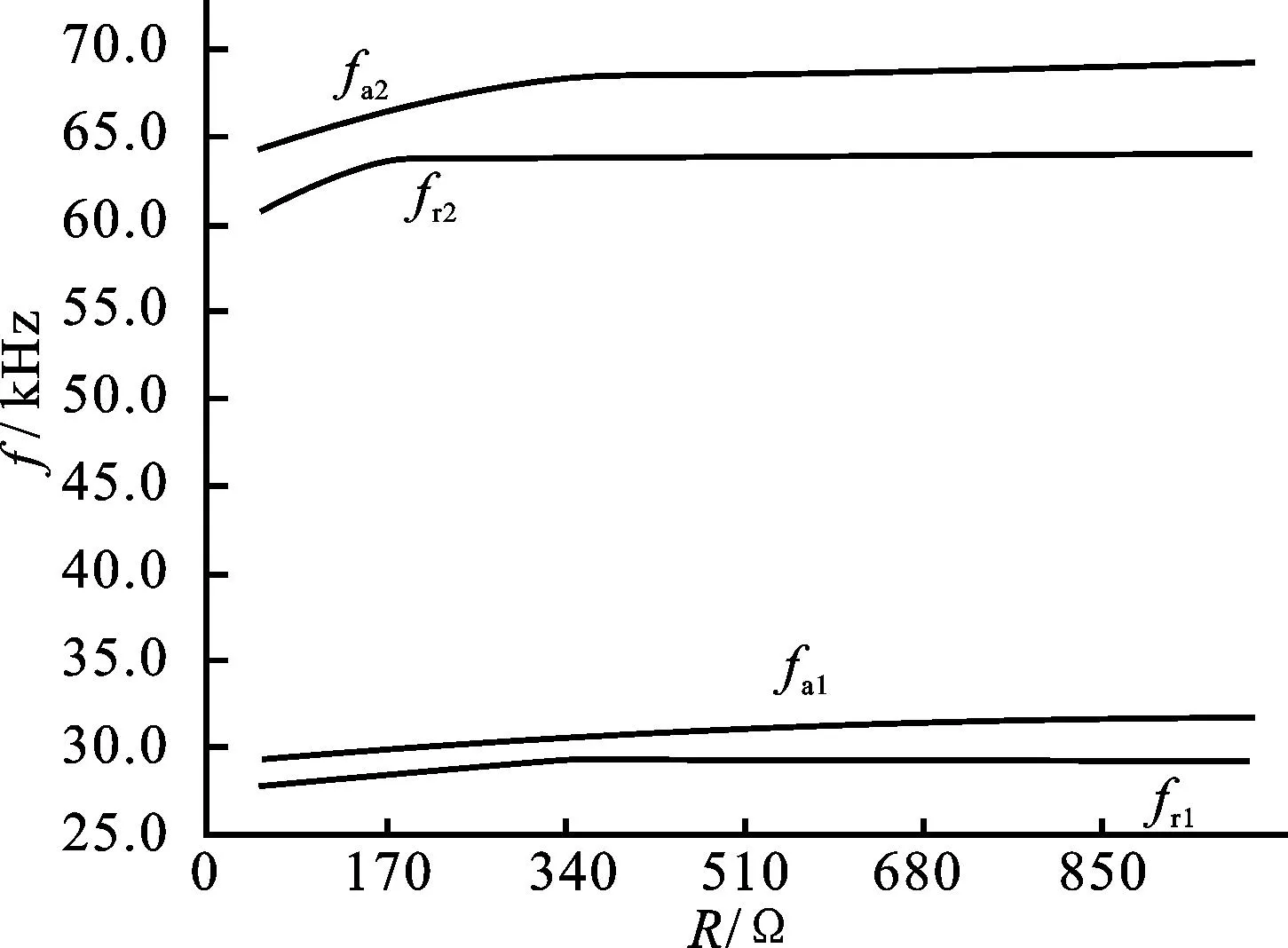
图6 压电变压器的共振及反共振频率与R的关系

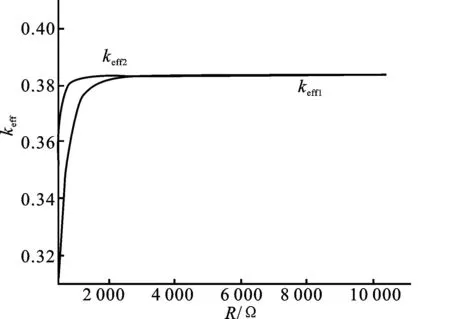
图7　机电耦合系数与R的关系

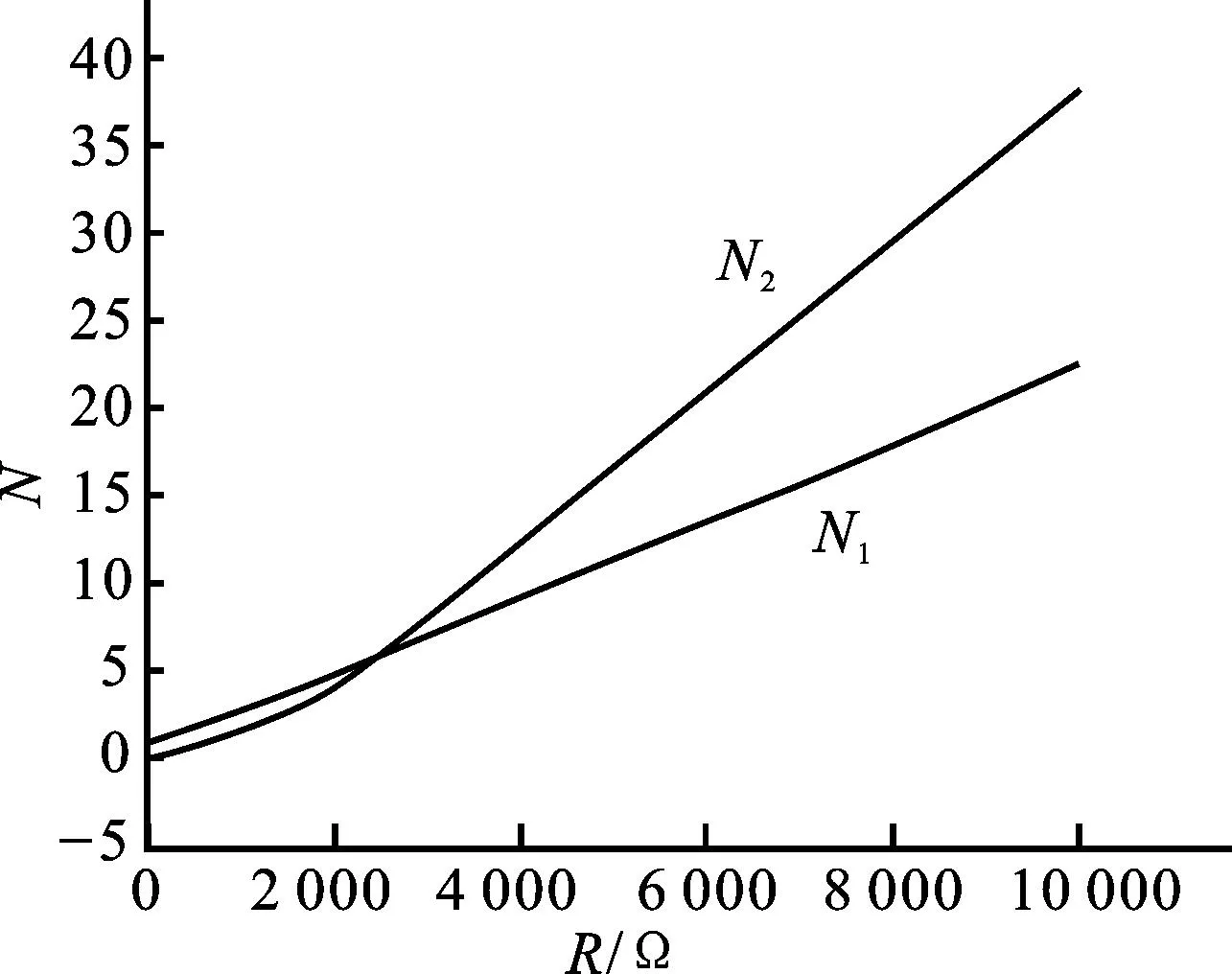
图8　电压增益与R的关系

由图6可得，在R比较小的时候，压电变压器一阶、二阶共振频率均随着输出端负载的增大而增大，而当R增大到一定值时，共振频率趋于稳定。不同的是，一阶模态下共振频率随负载的变化较小，二阶模态下共振频率随负载的变化较大。

由图7可得，在R=250 Ω附近，二阶有效机电耦合系数达到最小，R=450 Ω附近一阶有效机电偶和系数达到最小，变压器机械能与电能转换效率最低；而当R增大到1 600 Ω附近时，一阶、二阶有效机电偶和系数均趋于稳定。

由图8可以看出，变压器在一阶、二阶共振模态下的电压增益均随着R的增大而增大。

4变压器电压增益及电端输入总阻抗Zi1的频率特性分析

根据公式(21)、(24)可得出当负载R=100 Ω，l2=l3=0.02 m时变压器电压增益及电端输入总阻抗Zl1随频率的变化曲线如图9所示。

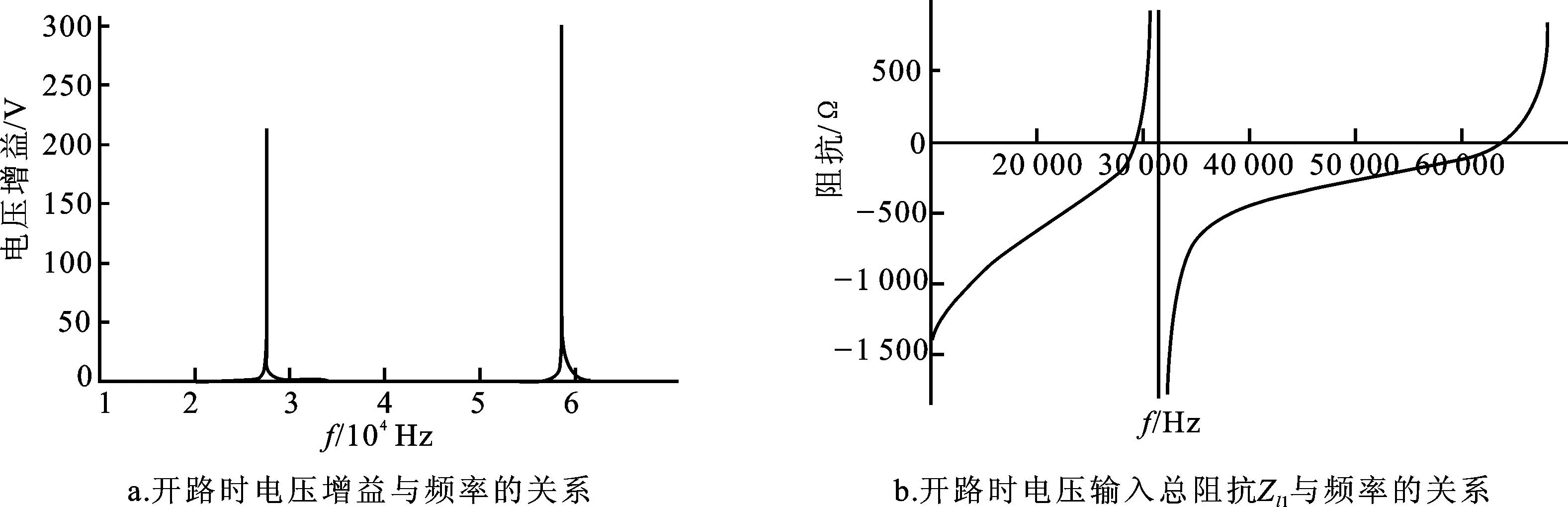
图9开路时电压增益(a)、总阻抗Zl1(b)与频率的关系

Fig.9The relationship of voltage transformation ratid(a), the input electrical impedanceZl1(b) with frequency

由图9可知，当阻抗为零时对应的即为变压器的共振频率，且在共振频率下变压器的电压增益最大。

5理论计算与ANSYS模拟结果的比较

为验证理论分析结果，用ANSYS模拟计算了不同尺寸下压电变压器的振动，仿真结果与计算结果的比较如表2、3所示，其中fr1、fa1、fr2、fa2分别表示一阶共振、反共振频率，二阶共振、反共振频率的理论计算结果，fr11、fa11、fr22、fa22表示对应ANSYS模拟的结果，Δr1=(fr1-fr11)/fr1、Δr2=(fr2-fr22)/fr2、Δa1=(fa1-fa11)/fa1、Δa2=(fa2-fa22)/fa2表示对应的误差值。

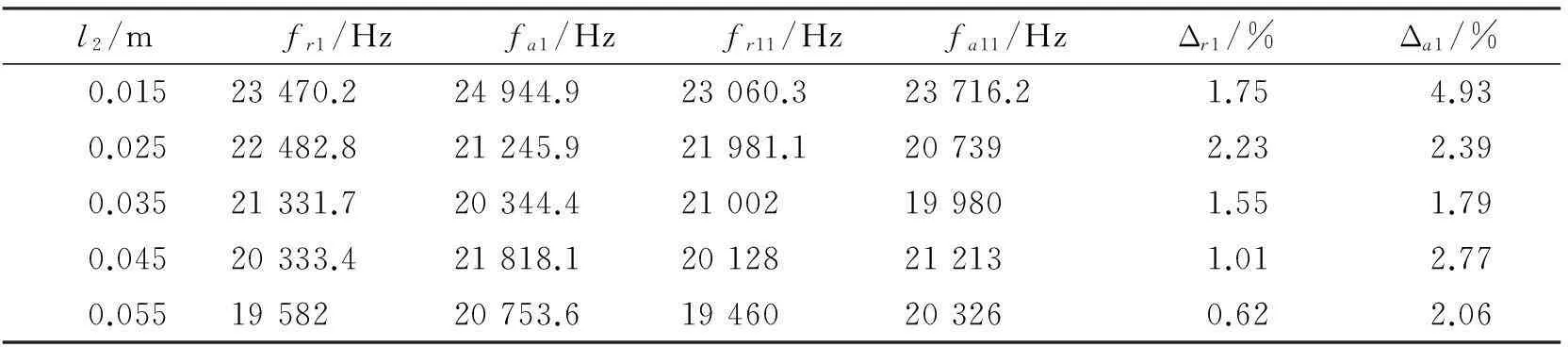
表2　一阶模态模拟值与解析解的比较

表3　二阶模态模拟值与解析解的比较

由表2可得，理论计算结果与ANSYS模拟计算一致，从而验证了理论计算结果的正确性。

6理论计算与实验测量结果的比较

为进一步验证理论分析结果，制作了一个结构如图1的压电换能器，其各项几何参数分别为R=0.015 m,l1=0.03 m,l2=0.02 m,l3=0.05 m,l0=0.003 m,P1=P2=4,物理参数由表1给出。

经阻抗分析仪测得了短路情况下的一阶共振、反共振频率分别为frs1、fas1，对应的理论值为frs、fas，相对误差为Δrs=(frs-frs1)/frs、Δas=(fas-fas1)/fas。各项数据如下：frs1=17 582 Hz,fas1=18 040 Hz,frs=17 933 Hz,fas=18 837 Hz,Δrs=1.96%,Δas=4.23%。所以，理论计算结果与实验测量结果一致，进一步验证了理论计算结果的正确性。

7结论

本文设计了一种由三段金属块和两组压电片组成的新型夹心式压电变压器。通过等效电路法推导出了压电陶瓷变压器的一阶、二阶共振频率，反共振频率，电压增益，有效机电耦合系数的解析表达式以及在一定条件下几何尺寸和负载对以上参数的影响,并对共振频率和反共振频率进行了有限元分析。得出以下结论：

(1) 负载R为定值时，改变金属块l2、l3的长度可以发现，一阶模态下共振、反共振频率随着中间金属长度l2的增大而减小；有效机电耦合系数有最大值。二阶模态下的共振、反共振频率均存在最大值；有效机电耦合系数有最小值；电压增益有最大值。

(2) 变压器尺寸固定时，改变负载电阻可以发现，在R比较小的时候，压电变压器共振频率均随着随输出端负载的增大而增大，而当R增大到一定值时，共振频率趋于稳定；有效机电偶和系数均有最小值且当R增大到1 600 Ω附近时，有效机电偶和系数均趋于稳定；电压增益均随着R的增大而增大。

(3)在尺寸、负载均固定的情况下，变压器电压增益在共振频率附近最大。

参考文献:

[1] ERHART J. Bulk piezoelectric ceramic transformers[J]. Advances in Applied Ceramics,2013,112(2): 91-96.

[2] 薛蕙，高适.压电陶瓷变压器及其应用[J].磁性元件与电源,2012(12):129-136.

[3] 毛兴武，张乃国.压电陶瓷变压器[J].电子元器件应用,2011,13(9):53-57.

[4] 黄以华,周康源,陈昕，等.压电陶瓷变压器的发展:回顾与展望[J].声学技术,2002,21(3)：122-128.

[5] 林书玉. 压电陶瓷变压器及其应用现状[J]. 陕西师范大学学报(自然科学版),2008,36(2)：26-32.

[6] 林书玉.功率超声技术的研究现状及其最新进展[J]. 陕西师范大学学报(自然科学版),2001,29(1)：101-106.

[7] 林书玉.夹心式功率超声压电换能器负载特性研究[J]. 陕西师范大学学报(自然科学版),2002,30(2)：29-34.

[8] 林书玉.超声技术的基石:超声换能器的原理及设计[J].物理,2009,38(3):141-148.

[9] 林书玉.功率超声换能振动系统的优化设计及其研究进展[J].陕西师范大学学报(自然科学版),2014,42(6):31-39.

[10] 栾桂冬，张金铎,王仁乾. 压电换能器和换能器[M].北京:北京大学出版社,2005:1-7.

[11] 李果，林书玉.一种新型阶梯盘形压电陶瓷变压器[J].压电与声光,2014,36(1)：47-52，57.

[12] LIN S Y, XU C L. Analysis of the sandwich ultrasonic transducer with two sets of piezoelectric elements[J]. Smart Materials and Structures,2008,17(6):065008.

[13] LIN S Y. Effect of electric load impedances on the performance of sandwich piezoelectric transducers[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2004, 51(10):1280-1286.

〔责任编辑 李博〕

第一作者： 邓立娟，女，硕士研究生，研究方向为石墨烯电学性质。E-mail: 499097568@qq.com

Characteristics of new sandwich piezoelectric ceramic

ultrasonic composite transformer

QIAO Xiaoyang, LIN Shuyu*

(School of Physics and Information Technology, Shaanxi Key Laboratory of Ultrasonic,

Shaanxi Normal University, Xi′an 710119, Shaanxi, China)

Abstract:A new type of the longitudinally polarized sandwich piezoelectric ceramic ultrasonic transformer was proposed. Using the equivalent circuit method the electromechanical characteristics of the piezoelectric vibrator was analyzed. The analytical solutions of the input impedance, the resonance frequency, the anti-resonance frequency, the voltage gain were obtained. The relationships of the resonance frequency, anti-resonance frequency, the electromechanical coupling coefficient, the voltage gain and the longitudinal lengths of the transformer, electric load resistance were obtained. The electromechanical coupling coefficient of first resonance mode has the maximum value in the certain size or electric load resistance. The voltage gain of first resonance mode has the maximum value in the certain size.The ANSYS simulation and the measured value of resonance frequency verified the analytical results. The results show that the simulation results and the experimental results agreed with the calculated results.

Keywords:piezoelectric transformer; longitudinal vibration; equivalent circuit; resonance; voltage gain

通信作者：* 阎维贤，教授，博士。E-mail:yanwxsxu@163.com

基金项目：国家基础科学人才培养基金(J1103210)

收稿日期：2015-07-18

doi:10.15983/j.cnki.jsnu.2016.01.216

文章编号：1672-4291(2016)01-0049-05

中图分类号:TM433

文献标志码:A