基于改进支持向量机的船舶纵摇预报模型

摘 要：为了提高船舶纵摇预报的精度，本文提出一种基于粒子群优化算法和灰色模型改进的支持向量机预报模型，首先通过灰色模型对原始纵摇数据进行处理，再通过粒子群算法对支持向量机的参数进行优化，使其获得最优的训练效果以提高预测精度，最后使用大连海事大学教学试验船”玉鲲”的实船纵摇数据对模型进行仿真测试，实验结果表明该模型具有较高的预测精度。

关键词：支持向量机；粒子群优化算法；纵摇预报；灰色模型

中图分类号：U652.3 文献标识码：A 文章编号：1006—7973（2016）10-0042-03

在船舶航行的过程中，由于船舶受到海浪、海风等环境因素的干扰，会产生横摇、纵摇、艏摇、横荡、纵荡、垂荡这6个自由度的运动，对于横摇运动目前可以通过减摇等装置以及其它控制方法达到缓解横摇角的目的，但对于纵摇运动，目前还没有有效的抑制方法，通常通过预报技术对危险时段进行预报减少事故的发生。因此对纵摇模型的精确建模与提高纵摇预测的精度一直是船舶运动领域的重要研究课题。

目前国内外有很多学者对船舶纵摇预测的方法展开了研究，Wiener等人利用统计预报的方法实现了船舶纵摇的预测、Triantafyllou等人使用卡尔曼滤波法对船舶纵摇进行了预测、马洁等人利用多层递阶预报模型对大型船舶进行了纵摇的预测。

相比于上述算法，人工智能算法在船舶纵摇预测中使用较少，因此在本文中我们提出了一种基于灰色模型和粒子群优化算法改进的支持向量机船舶纵摇预测模型，支持向量机相比于其它神经网络具有更好的自适应能力且在预测过程中由于遵循结构风险最小化原则不易陷入局部最优，此外通过优化算法进一步对支持向量机的预测精度进行了提升。在整个预测模型中支持向量机用于纵摇数据的非线性回归，灰色模型用于纵摇数据的预处理，该数据预处理方法能够提取数据中的有效信息，缓解由于船舶自身载态以及环境的不确定性对预报精度造成的影响。此外粒子群优化算法用于支持向量机的参数优化使支持向量机能够获取最佳的训练效果，以提高预测精度。仿真结果证明该方法能够有效实现船舶纵摇的预测，具有较高的预测精度。

1 支持向量机、灰色模型以及粒子群优化算法的理论基础

支持向量机是在1995年第一次被Vapnik提出的，与传统神经网络不同的是，支持向量机并非采用经验风险最小化准则，而是结构风险最小化的近似实现。这使得支持向量机在训练过程中不易陷入局部最优，因此不存在局部最小问题。此外，支持向量机基于统计学理论，它具有严格的理论基础和数学基础，它在处理非线性回归以及高维模式识别等问题中具有许多特有的优势。

灰色系统理论是由我国学者邓聚龙教授于1982年提出来的，该系统时用于研究数量少、信息贫瘠等不确定性问题的理论方法。通过对部分已知信息的生成、开发，提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控。

灰色模型在处理数据时需通过以下三个步骤的处理，第一步为累加操作，第二步将累加后的数据在相应的预测模型中进行计算，最后通过反向累加操作实现数据的还原。

粒子群优化算法（Particle Swarm Optimization， PSO）是计算智能领域，除了蚁群算法、鱼群算法之外的一种群体智能的优化算法，该算法最早是由Kennedy和Eberhart在1995年提出来的。在使用支持向量机对潮汐进行预报时，我们通过粒子群优化算法对支持向量机的参数c和g进行优化来获得最佳的训练效果，以提高潮汐预报的精度，其中c为SVM惩罚系数，g为核函数半径。

2 支持向量机参数的选择以及模型的确立

2.1 自回归预测模型

本文在描述纵摇变化的过程中选用自回归模型（Auto Regressive， AR），AR模型基于统计学理论，它能够有效的处理时间序列并能够较为清晰地描述序列的变化情况，适合于船舶纵摇预报。AR模型的表达式如下所示：

（1）

式（1）为n阶AR模型的单步预测模型，记为AR（n）。n代表模型的阶数，为模型参数，为随机噪声。当n阶AR模型用来表示纵摇时，代表第t秒的纵摇角，表示第t-n秒的纵摇角，为随机噪声。

阶数n在本次实验中通过对不同阶数的AR模型进行测试确定，选取产生绝对误差最小的阶数确定AR模型，绝对误差计算公式如下所示：

其中n为样本数目，和 分别代表纵摇的实测值和预测值。

通过对1～8阶AR模型的绝对误差进行计算，当AR模型的阶数为2时，绝对误差MAE=0.53，相比于其它阶数，该阶数的AR模型在训练过程中的绝对误差最小，拥有更好的预测能力，所以在本次仿真中AR模型的阶数设置为2。

2.2 支持向量机参数选择

支持向量机的参数设置对预测结果具有很大影响，一个合适的参数设置会使支持向量机具有较好的预测效果，而相反不恰当的参数设置则很可能影响其预测效果。

其中c和g的选择是由粒子群优化确定的，在粒子群优化过程中c和g的取值范围设定为[0，100]，粒子群进化代数为200，种群数量设为20，参数局部搜索能力和参数全局搜索能力分别设置为1.5和1.7，速度最大和最小值分别为5和-5。

优化后的c选为18.89，g为1.07。在核函数以及支持向量机类型的选择上我们分别选择RBF核函数以及-SVM，两者具有较高的回归准确率与预测精度，适合于纵摇的预测。

2.3 改进的支持向量机

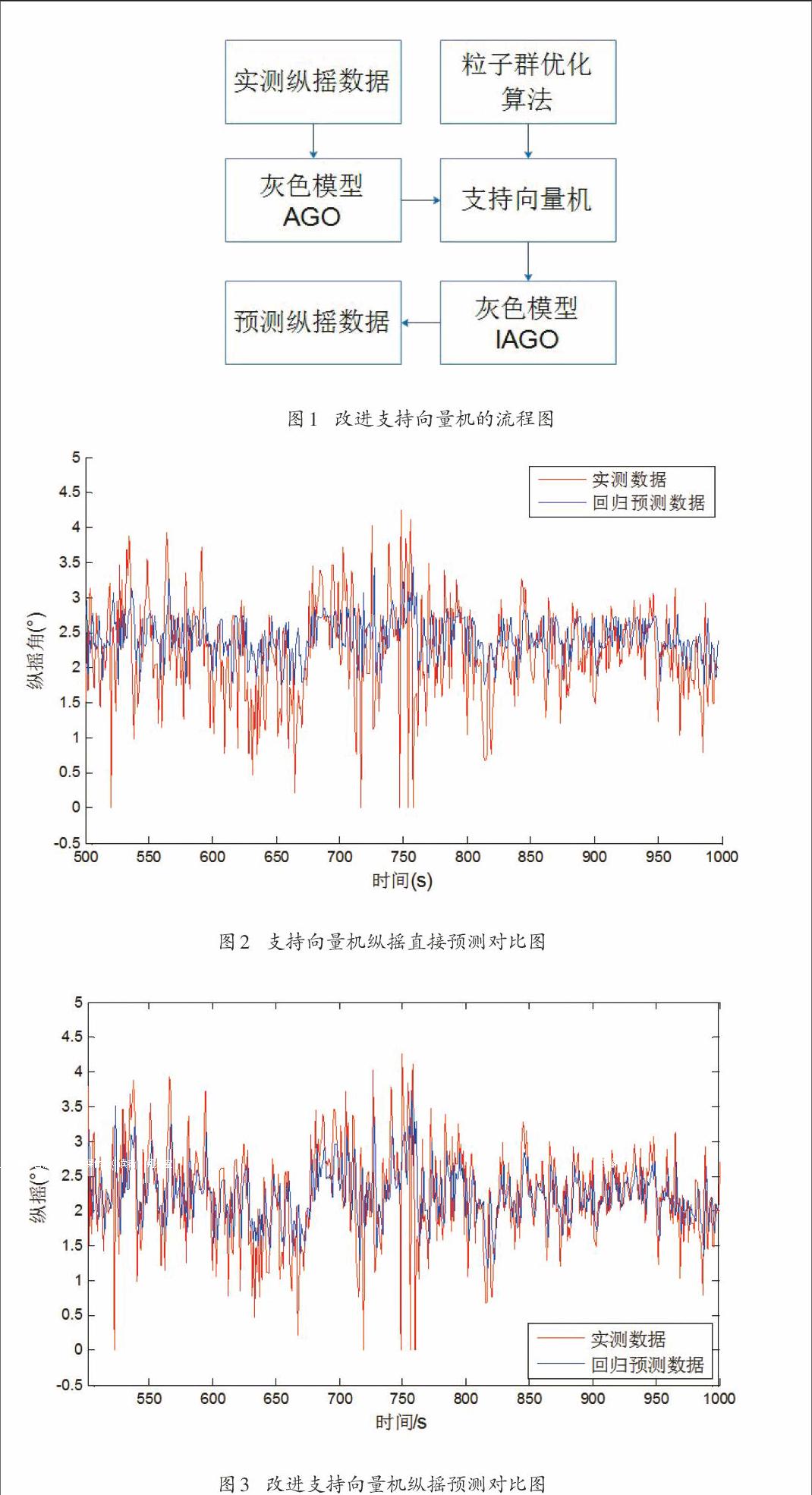
该模型的结构流程图如图1所示：

如图1所示，该模型在进行纵摇预测时首先需要获取实船纵摇数据作为输入，但由于纵摇在测量过程中受到船体自身载态以及环境等因素等影响，实测纵摇数据具有较高的不确定性以及测量误差，所以该部分数据首先经过灰色模型AGO操作，处理后的数据相比于原始数据具有更明显的规律性，该部分数据可作为支持向量机输入应用于纵摇预报，在预报过程中通过粒子群算法对支持向量机进行优化，选取支持向量机的惩罚系数c和核函数半径g，利用该值对支持向量机的训练模型进行设置，之后可以获得精度较高的纵摇的预测值，该值还需要进行IAGO操作以还原数据，得到最终的纵摇预测结果。

3 仿真结果

本文的实验数据均取自大连海事大学教学实验船“玉鲲”轮，数据记录的为船舶在公海上航行时的纵摇数据，记录间隔为1s。一共选取1000个连续的纵摇数据用于本次实验，其中500个数据作为输入用于支持向量机的网络训练，另500个纵摇数据用于测试和验证模型的预测效果，对支持向量机的参数设置均选用上一章选取的值。

图2是使用支持向量机对纵摇直接预测的结果，图3是使用改进支持向量机对纵摇预报的结果：

从图2中我们可以看出，虽然使用支持向量机对纵摇直接预测基本能反映纵摇变化的趋势，但其误差也是相对较大的，而利用改进的支持向量机预测的纵摇数据与实测纵摇数据的吻合程度要明显高于用支持向量机直接预测的方法。

为了更精确地分析改进方法在精度上的优势，在本文中提出了均方根误差RMSE作为纵摇预测误差大小的评判标准，其表达式为：

其中L为纵摇在仿真中的样本数目，y和 分别代表纵摇的实测值和预测值。

经过仿真得出，支持向量机直接预测的RMSE为0.7351°，预测时间42.75s；改进支持向量机预测的RMSE为0.6428°，预测时间67.43s；BP神经网络预测的RMSE为0.8016°，预测时间20.37s。由此可知，改进的支持向量机相比于直接使用支持向量机进行预测的方法虽然在预测时间上略有增加，但在精度上有了较大的提升。并且相比于其它神经网络，支持向量机在预测精度上有较大的优势，证明该方法适用于船舶的纵摇预测。

4 结论

在船舶航行时，由于船舶自身操作的不可预知以及受到不同海况的影响，造成船舶纵摇运动复杂性和不确定性。为了能够准确预测船舶纵摇运动，本文提出了基于改进支持向量机的船舶纵摇预报模型，通过对支持向量机建立单步预测模型，并利用灰色模型以及粒子群算法对数据以及模型参数进行优化提高了模型预测精度，并使用预测模型对实际船舶纵摇数据进行建模，根据实船数据特点确定船舶纵摇数据间的预测关系，确定了支持向量机的输入结构，并应用模型对船舶纵摇进行了短期的预报，验证了模型的效果，测试证明该模型适用于船舶的纵摇预测并具有较高预测精度。

参考文献：

[1] 杨丽丽. 基于GM模型进行舰船纵摇参数预测[J]. 国外电子测量技术， 2013， 32（3）：55-57.

[2] 马洁. 船舶纵摇运动预报AR法与多层递阶方法比较研究[J] 中国智能自动化会议. 2009.pp1040-1047.

[3] Wiener N. Extrapolation， interpolation， and smoothing of stationary time series， with engineering applications [M]. Technology Press of the Massachusetts Institute of Technology ；， 1950.

[4] Triantafyllou M S， Bodson M B. Real Time Prediction of Marine Vessel Motions[J]， Using Kalman Filtering Techniques. 1982.

[5] 马洁， 刘小河， 李国斌，等. 大型舰船纵摇运动的多层递阶预报[J]. 船舶工程， 2006， 28（1）：5-8.

[6] Cortes C， Vapnik V Support-vector networks. Machine learning [J]， vol.20， no.3， pp.273-297（1995）.

[7] Zhang X G， Zou Z J. Application of Wavelet Denoising in the Modeling of Ship Manoeuvring Motion[J]. Journal of Ship Mechanics， 2011， 15（6）：616-621.

[8] 丁世飞， 齐炳娟， 谭红艳. 支持向量机理论与算法研究综述[J].电子科技大学学报，2011，40（1）：2-10.

[9]邓聚龙. 灰色预测与决策[M]. 华中理工大学出版社，1998

[10]Kennedy J， Eberhart R C. Particle Swarm Optimization [J]. Proceedings of IEEE International Conference on Neural Networks， 1995， 1942-1948.

基金项目：1.交通部应用基础研究项目2014329225010；2.辽宁省教育厅一般项目L2014214；3.中央高校基本科研业务经费项目3132016116