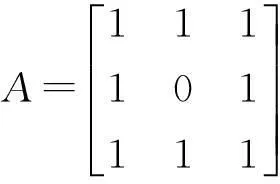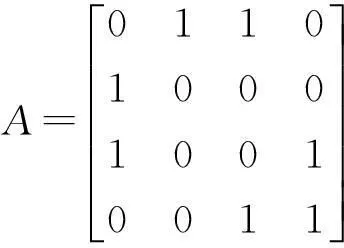稠密k-子图问题的双非负松弛

稠密k-子图问题的双非负松弛

郭传好,单而芳

(上海大学管理学院管理科学与工程系,上海200444 )

摘要：稠密k-子图问题是组合优化里面一类经典的优化问题,其在通常情况下是非凸且NP-难的。本文给出了求解该问题的一个新凸松弛方法-双非负松弛方法,并建立了问题的相应双非负松弛模型,而且证明了其在一定的条件下等价于一个新的半定松弛模型。最后,我们使用一些随机例子对这些模型进行了数值测试,测试的结果表明双非负松弛的计算效果要优于等价的半定松弛。

关键词：组合优化;双非负松弛;半定松弛;稠密k-子图

收稿日期：2014-01-23

基金项目：国家自然科学基金资助项目(11501350)

作者简介：郭传好(1980-),男,博士后,研究方向:最优化理论、算法及其应用;单而芳(1965-),男,教授,博士生导师,研究方向:图论及其应用。

中图分类号：O221.7文章标识码：A

Doubly Nonnegative Relaxation for Densestk-subgraph Problem

GUO Chuan-hao, SHAN Er-fang

(DepartmentofManagementScienceandEngineering,SchoolofManagement,ShanghaiUniversity,Shanghai200444,China)

Abstract:Densest k-subgraph problem is a classical problem of combinatorial optimization, which is nonconvex and NP-hard in general. In this paper, we propose a new convex relaxation method, i.e., doubly non-negative relaxation method, for solving this problem, and establish the corresponding doubly nonnegative relaxation model for the problem. Moreover, we prove that the doubly nonnegative relaxation model is equivalent to a new semidefinite relaxation model under some conditions. Finally, some random examples are tested by these relaxation models. The numerical results show that the doubly non-negative relaxation is more promising than the corresponding semidefinite relaxation.

Key words:combinatorial optimization; doubly nonnegative relaxation; semidefinite relaxation; densestk-subgraph

0引言

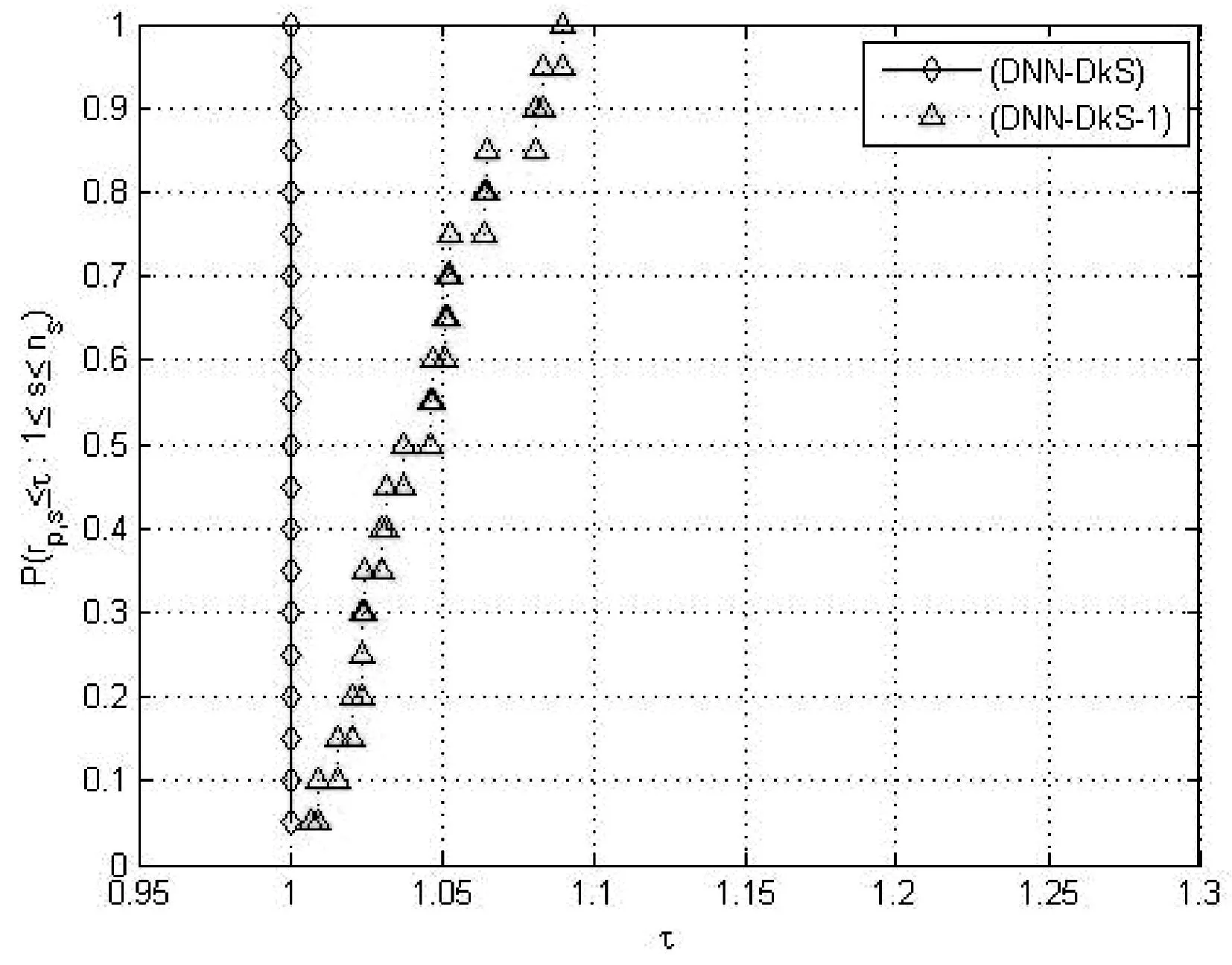
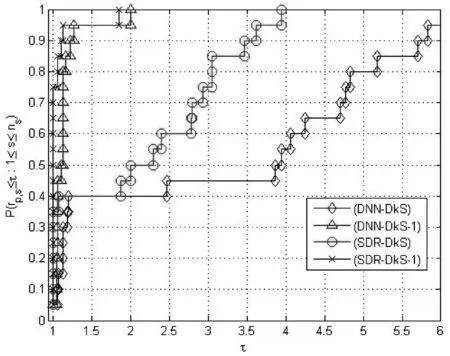
对于一个给定的图G(V,E),其中V表示图的顶点集,E表示图的边集.图G的稠密k-子图(Densest K -Subgraph,简记DkS)问题就是指:对任给一个参数k,寻找图G中一个具有k个顶点的子图,使得由这k个顶点所张成的子图的所有边所对应的权和最大.通常1

最近,Burer[3]为了处理一类全正规划[4](Completely Positive Programming)问题,借助于Dinanada分解定理[5],得到了一类易求解的凸规划问题,即双非负规划(Doubly Nonnegative Programming)问题.该问题具有多项式时间内点算法求解,而且还可以被许多凸规划软件求解.随后这一方法被许多学者做进一步的研究[3, 4, 6, 7].

本文基于文献[3]中方法的思想,对DkS问题的求解做进一步的研究. 首先, 根据DkS问题的结构特点, 我们建立其对应的双非负松弛问题模型,探讨分析其相应的模型特点.其次,还研究了双非负松弛问题与相应的半定松弛问题之间的关系,即在一定的假设条件下,这两类松弛问题具有一定的等价性.最后,大量的数值实验结果表明双非负松弛具有较好的计算效果相比较与等价的半定松弛问题.

1DkS问题数学模型

首先,简单回顾一下DkS问题的基本定义.

定义1DkS问题就是指:在给定的图G(V,E)上,寻找一个具有k个顶点的子图,使得由这k顶点所张成的子图的所有边所对应的权和最大,其中1

记A=(aij)n×n表示图G的加权邻接矩阵,注意A是对称的.则根据上面关于DkS问题的定义,可得该问题具有下面形式的数学表达式

s.t.xTe=k, (DkS)

x∈{0,1}n

s.t.xTx=k, (DkS-1)

x∈{0,1}n

不失一般性,假设A不正定,则(DkS)和(DkS-1)都是非凸的整数约束二次规划问题,其通常是NP-难的.因此建立其相应可计算松弛问题模型是求解它们的有效方法之一.

2双非负松弛模型

为了建立(DkS)的可计算松弛模型,同时注意到(DkS)和(DkS-1)中目标函数xTAx可以表示为A·xxT,其中·表示矩阵乘积的迹.记X=xxT,借助于向量的提升技术,则(DkS)和 (DkS-1)可分别被转化为下面的数学表达形式

类似于文献[4]中的定理2.6的证明,我们可以得到下面的定理,其证明过程在此省略.

定理2.1(i)(DkS)与(CPP-DkS)的最优值相等,(DkS-1)与(CPP-DkS-1)的最优值相等;(ii)如果(x*,X*)是(CPP-DkS)的最优解,则x*一定是(DkS)最优解的凸包,该结论对于(DkS-1)同样成立.

通过定理2.1,我们可以把(DkS)和(DkS-1)分别转化为(CPP-DkS)和(CPP-DkS-1),而且这种转化在某种意义下是等价的.同时注意到(CPP-DkS)与(CPP-DkS-1)本质上都是线性凸规划问题,我们希望其可以被一些现有的有效凸优化软件有效求解.但是注意到(CPP-DkS)和 (CPP-DkS-1)中都含有约束条件C1+n,Dickinson和Gijen[8]已经证明判断该条件的可行性是 NP-难的,所以(CPP-DkS)和(CPP-DkS-1)仍然是NP-难的,尽管其在形式上是凸问题.

值得庆幸的是,借助于下面的定理,C1+n可以被松弛为一个可计算的凸锥,这样(CPP-DkS)和(CPP-DkS-1)就可以被进一步转化为可计算的凸规划问题.定理内容如下:

根据定理2.2,(CPP-DkS)和(CPP-DkS-1)可以被松弛为下面的问题

至此,由于(DkS)和(DkS-1)等价,我们分别建立了其相应的可计算双非负松弛模型 (DNN-DkS)和(DNN-DkS-1).为了检验这些松弛模型的实际计算效果,下面我们将通过求解一些随机产生的例子来展现其实际计算性能,所有的例子都通过Matlab编程调用CVX软件进行求解.

首先使用模型(DNN-DkS)来求解可得

很容易验证关系X*=x*(x*)T成立,所以上面得到的解是原问题的最优解.其次使用模型(DNN-DkS-1)来求解该问题得Opt(DNN-DkS-1)=1.84447, 其中

此时关系X*=x*(x*)T不成立, 所以使用模型(DNN-DkS-1)求解得到的只是原问题的一个上界1.84447.

上述两个例子的测试结果表明尽管(DNN-DkS-1)和(DNN-DkS)同为原问题(DkS)的双非负松弛模型,因为(DkS-1)与(DkS)等价,但是(DNN-DkS)的计算效果要优于(DNN-DkS-1).

为了进一步比较(DNN-DkS)与(DNN-DkS-1)的计算效果,我们测试了一组随机产生的问题.

例3n=10,k=5,系数矩阵A按照下面的方式产生:rand(‘seed’, seed);G=(rand(n)<=0.5);A=round(20*rand(n)-10);A=triu(A, 1);A=A.*G;A=A+A’,其中seed=1,2,…,20.

图1　最优值的性能描述

图2　迭代次数的性能描述

3与半定松弛的关系

注意上一节我们所建立的(DkS)的两个双非负松弛模型(DNN-DkS)和(DNN-DkS-1) 中,约束条件D1+n其也可以视为半定约束加上一组线性不等式约束,这样这些松弛模型在表达形式上就可以视为半定松弛模型,这与通常的半定松弛模型有什么关系？下面我们将研究双非负松弛与半定松弛之间的关系.

首先注意到约束条件x∈{0,1}n⟺y∈{-1,1}n,y:=2x-e因此(DkS)和(DkS-1)也可以分别被等价的转化为下面的问题

记Y=yyT,结合y∈{-1,1}n,易得1+yi+yj+Yij≥0,1≤i≤j≤n.利用yTAy可以表示为A·yyT,通过半定松弛技术,我们分别可得(DkS)和(DkS-1)的半定松弛模型如下

如上所述,我们又分别给出了(DkS)两个新的半定松弛模型(SDR-DkS)和(SDR-DkS-1).下面的定理将进一步给出前一节所建立的双非负松弛模型(DNN-DkS)和(DNN-DkS-1)分别与上面两个半定松弛模型之间的关系.

定理3.1如果(DNN-DkS)与(SDR-DkS)的可行域都是非空的,那么(DNN-DkS)与(SDR-DkS)等价,即它们不仅最优值相等,而且最优解也可以相互的表示.同理,如果 (DNN-DkS-1)与(SDR-DkS-1)的可行域都是非空的,那么(DNN-DkS-1)与(SDR-DkS-1)也是等价的.

即Opt(SDR-DkS)≥Opt(DNN-DkS).

综合上面的证明可得Opt(DNN-DkS)=Opt(SDR-DkS),而且它们的最优解可以相互的表示,所以(DNN-DkS)与(SDR-DkS)等价.对于(DNN-DkS-1)和(SDR-DkS-1)的等价性,可采用类似上面的证明方法,其证明过程与上面类似,在此省略.

定理3.1表明问题(DkS)的双非负松弛模型,其实际上也等价于一个半定松弛模型.尽管如此,双非负松弛模型自身的特殊结构特点还是蕴含了其具有一些较好的计算效果,相对比与半定松弛模型.下面就对一些使用随机函数生成的问题(DkS),分别使用这些松弛模型求解,来进一步说明双非负松弛模型的计算效果优势.

例4n=20,k=5,系数矩阵A按照下面的生成方式产生:seed=1,2,…20; randn(‘seed’,seed);A=round(randn(n,n));A=tril(A,-1)+triu(A’, 0).

下面图3和图4分别给出了使用(DNN-DkS),(DNN-DkS-1),(SDR-DkS)和(SDR-DkS-1)求解这组问题的最优值与迭代次数结果相比的性能描述.从图3中最优值比较结果显然可得(DNN-DkS)与(SDR-DkS)具有相同的性能,(DNN-DkS-1)与(SDR-DkS-1)具有相同的性能,而且(DNN-DkS)和(SDR-DkS)的性能要优于(DNN-DkS-1)与(SDR-DkS-1)的性能.同时在测试的过程中, (DNN-DkS)与(SDR-DkS)分别能够求得其中8个问题的最优解, 而(DNN-DkS-1)与(SDR-DkS-1)所得到的只是近似解.从图4中迭代次数的性能比较结果可知(DNN-DkS-1)和(SDR-DkS-1)的性能比较好,要优于(DNN-DkS)与(SDR-DkS)的性能.但对于实际中的问题,特别是在一些高性能计算机的辅助条件下,我们更多关注的是问题最优值或近似解的情况,因此从这个意义上来说双非负松弛模型(DNN-DkS)的性能更好一些.

图3　最优值的性能描述

图4　 CT二次接线板宏观图片

为了进一步验证双非负松弛模型的计算效果优势,我们对下面几个高维的例子做进一步的数值实验测试,数值结果进一步说明了双非负松弛模型(DNN-DkS)具有较好的计算效果,相比较与半定松弛模型.

例5n=30,k=10,矩阵A按照下面的方式产生:randn(‘2012’,2012),A=randn(n,n),A=tril(A, -1)+triu(A’,0).

下面使用(DNN-DkS)求解该问题可得Opt(DNN-DkS)=30.5894,迭代次数为52.而使用 (SDR-DkS)求解得Opt(SDR-DkS)=30.5903和迭代次数是70.很显然,不仅 Opt(DNN-DkS)≤Opt(SDR-DkS),而且相应的求解迭代次数要优于(SDR-DkS)的.如果使用(DNN-DkS-1)和(SDR-DkS-1)来求解该问题得Opt(DNN-DkS-1)=Opt(SDR-DkS-1)=31.1136,而迭代次数分别为25和23.尽管使用(DNN-DkS-1)和(SDR-DkS-1)求解的迭代次数较少,但是它们所得到的最优值要大于(DNN-DkS)的,所以总得来说使用(DNN-DkS)求解的效果较好.

例6n=40,k=15,randn(‘7’, 7),系数矩阵A=tril(randn(n,n), -1)+triu(randn(n,n)’, 0).

调用(DNN-DkS)求解可得Opt(DNN-DkS)=53.2917和迭代次数52.而使用(SDR-DkS)求解Opt(SDR-DkS)=53.2925和迭代次数81.同样,使用(DNN-DkS-1)和(SDR-DkS-1)来求解该问题可得Opt(DNN-DkS-1)=Opt(SDR-DkS-1)=53.8104,而迭代次数分别为24和23.综合分析可得 (DNN-DkS)求解的效果较好.

例7n=90,k=25,randn(‘228’, 228),系数矩阵A=tril(round(randn(n,n)),-1)+triu(round(randn(n,n)’), 0).

调用(DNN-DkS)求解该问题可得Opt(DNN-DkS)=163.344,迭代次数为82,而使用 (SDR-DkS)求解得Opt(SDR-DkS)=163.361≥163.344和迭代次数12982.很明显,使用双非负松弛模型(DNN-DkS)求解具有非常好的计算效果.同样,使用(DNN-DkS-1)和(SDR-DkS-1)来求解该问题可得Opt(DNN-DkS-1)=Opt(SDR-DkS-1)=167.421,而迭代次数分别为36和34.综合分析可得使用双非负松弛模型(DNN-DkS)求解具有非常好的计算效果.

4结论

本文研究了组合优化里面一类经典的优化问题-(DkS)问题.该问题在一般情形下是非凸且NP-难的,因此建立该问题的可计算凸松弛模型是有效求解此问题的方法之一.文中首先建立了问题的双非负松弛模型,并分析了其相应特性.然后证明了在一定的假设条件下,该双非负松弛模型等价于一个半定松弛模型.最后通过大量的随机例子来测试了这些松弛模型的各自计算效果.数值结果表明双非负松弛模型具有较好的计算效果相对比与半定松弛模型.

参考文献：

[1]Corneil D G, Perl Y. Clustering and domination in perfect graphs[J]. Discrete Applied Mathematics, 1984, 9(1): 27-39.

[2]Goldstein D, Langberg M. The dense-subgraph problem[R]. arXiv preprint arXiv: 0912. 5327, 2009.

[3]Burer S. Optimizing a polyhedral-semidefinite relaxation of completely positive programs[J]. Mathematical Programming Computation, 2010, 2(1): 1-19.

[4]Burer S. On the copositive representation of binary and continuous nonconvex quadratic programs[J]. Mathematical Programming, 2009, 120(2): 479-495.

[5]Diananda P H. On non-negative forms in real variables some or all of which are non-negative[C]. Mathematical Proceedings of the Cambridge Philosophical Society, 1962, 58(1): 17-25.

[6]Bai Y Q, Guo C H, Sun L M. A new algorithm for solving nonconvex quadratic programming over an ice cream cone[J]. Pacific Journal of Optimization, 2012, 8(4): 651-665.

[7]Bomze I M. Copositive optimization-recent developments and applications[J]. European Journal of Operational Research, 2012, 216(3): 509-520.

[8]Dickinson P J C, Gijben L. On the computational complexity of membership problems for the completely positive cone and its dual[R]. Johann Bernoulli Institute for Mathematics and Computer Science, University of Groningen, The Netherlands, 2011.

[9]Grant M, Boyd S, Ye Y Y. CVX: Matlab software for disciplined convex programming[M]. 2008.

[10]Dolan E D, Moré J J. Benchmarking optimization software with performance profiles[J]. Mathematical Programming, 2002, 91(2): 201-213.