Spark环境下基于频繁边的大规模单图采样算法
2017-09-15李龙洋董一鸿严玉良陈华辉钱江波
李龙洋 董一鸿 严玉良 陈华辉 钱江波
(宁波大学信息科学与工程学院 浙江宁波 315211)
Spark环境下基于频繁边的大规模单图采样算法
李龙洋 董一鸿 严玉良 陈华辉 钱江波
(宁波大学信息科学与工程学院 浙江宁波 315211)
(sgavin1991@163.com)
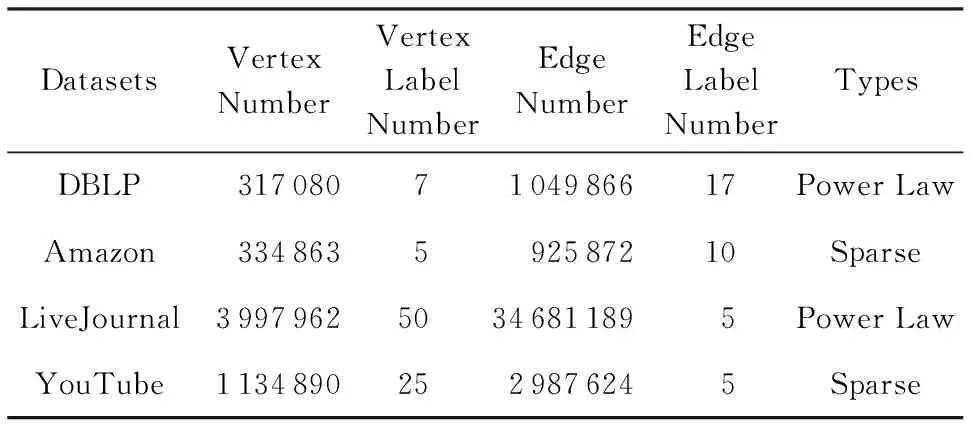
随着社交网络的流行,对其进行频繁子图挖掘的需求越来越强烈.大数据时代的到来,社交网络规模不断扩大,频繁子图挖掘工作变得愈发困难.在实际应用中,往往并不需要精确地挖掘出频繁子图,采样的方法在保证一定准确率的前提下能够显著提高频繁子图挖掘的效率.现有采样算法大多是根据节点的度进行采样,不适用于频繁子图挖掘.提出了一种基于频繁边的采样算法DIMSARI(distributed Monte Carlo sampling algorithm based on random jump and graph induction),在蒙特卡罗算法的基础上增加了根据频繁边进行随机跳的操作,并对其结果进行了图感应操作,进一步增加了算法的准确性,并在理论上证明了该方法的无偏性.实验结果显示:使用DIMSARI算法采样后进行频繁子图挖掘,准确性比现有其他的采样算法有较大的提高,在不同的采样率下采样后的子图的节点度都保持更小的归一化均方偏差.
采样;频繁子图;大规模单图;频繁边;Spark
现实生活中,人与人、人与物之间的关系可以用图的形式来表示,节点表示实体对象,边表示实体对象之间的关系.社交网络、生物信息网络等规模不断扩大,结构复杂.例如,作为全球最流行的社交平台,截至2015年6月,Facebook的单日活跃用户数量为9.68亿[1],大部分图挖掘算法复杂度较高,对于这样的社交网络进行子图同构、频繁子图挖掘都属于NP难问题.特别在当前大数据背景下,大规模单图(指连通图)的频繁子图挖掘算法的运行时间较久,尤其在支持度较低的情况下无法解决.在实际频繁子图挖掘以及子图同构等图操作中,并不需要精确地得到原始连通图的频繁子图个数或子图同构个数等,故对原始连通图进行采样后进行频繁子图挖掘,虽然在一定程度上降低了挖掘的准确性,但可以显著地提高频繁子图挖掘的效率,在保证一定准确率的前提下对原始图进行采样[2]是解决大规模图中频繁子图挖掘的有效手段.
传统的采样方法主要是根据节点的度转移进行采样,且偏于度比较高的节点,不适用于频繁子图挖掘.为了更好地完成频繁子图挖掘的任务,本文提出了一种基于随机跳和图感应的蒙特卡罗采样算法(Monte Carlo sampling algorithm based on random jump and graph induction, MSARI),并将其扩展到Spark平台下DIMSARI(distributed Monte Carlo sampling algorithm based on random jump and graph induction)算法,以处理大规模单图.首先,根据频繁边的分布使用蒙特卡罗算法进行图采样.为了降低频繁边的方差,采样过程中对当前边和将要跳转边进行频繁度比较,如果跳转边的频繁度小于当前边的频繁度,则跳转,否则停留在原处.最后进行图感应操作,将采样过程中丢失的子图边进行补全,增加算法的有效性.
本文的主要贡献如下:1)传统的采样算法多是根据节点扩展,本文则根据频繁边的分布进行蒙特卡罗采样,并在其基础上增加了随机跳转和图感应操作,提出MSARI算法,并扩展到Spark平台下的DIMSARI算法.将采样后的结果使用在频繁子图挖掘中,提高了频繁子图挖掘算法的效率.2)对比实验显示,在相同的采样率下DIMSARI算法采样后的子图进行频繁子图挖掘具有更高的准确率,在相同的准确率下该算法采样量更少,且采样后的子图结构与原始图更相似.
1 相关工作
图采样算法分为基础采样、随机游走采样、蒙特卡罗采样和基于拓扑结构的采样.
基础采样算法包括随机边采样[3]和随机节点采样[3].随机节点采样均匀地对节点进行采样,无法保持幂率性;而随机边采样则是随机均匀地选择边,得到的边的结果非常稀疏无法保持较大的直径.2011年Ahmed等人[4]在随机边采样基础上加入了图感应技术;2014年Blagus等人[5]对图感应算法进行了扩展,证明了图感应算法可以增加算法的准确性.然而,由于基础采样算法本身的随机性,即使增加图感应操作也无法达到较高的精度.
随机游走采样算法包含RW[6](random walk),FF[7](forest fire),RJ[7](random jump),BFS[8](breadth first search),1996年Lovász等人[6]提出随机游走(RW)算法,以初始节点的邻接节点进行扩展采样.2005年Leskovec等人[7]提出了森林火灾模型(FF)和随机跳(RJ)算法,FF算法随机生成一个种子节点,扩展的过程中以阈值来控制采样,该方法会陷入局部区域,且偏向于度较高的节点.RJ算法以修正的概率跳转到原始图的任一节点,有效避免陷入局部区域.2007年Ahn等人[8]提出BFS算法,该算法是广度搜索的采样方式.随机游走算法以初始节点的邻接节点扩展采样,一定程度上增加了采样的有效性,但采样结果容易陷入局部区域,且有偏向度较高的节点,不能很好地保持原始连通图的结构.
蒙特卡罗采样算法主要是利用蒙特卡罗模型来进行采样,2011年Gjoka等人[9]提出的蒙特卡罗散列随机游走算法使用了蒙特卡罗算法通过对Facebook数据集的验证,2011年Long等人[10]对其增加了随机跳的改进,这2种算法偏向度比较高的节点,不适用于采样后进行频繁子图挖掘.
基于拓扑结构的采样算法主要是利用原始图的拓扑结构进行采样.2011年Yoon等人[11]提出了基于社区划分的图采样算法,2014年Du等人[12]根据图的拓扑分层信息进行采样,以直径上的任一点为初始节点,根据与该初始节点的距离进行采样.2015年Rezvanian等人[13]以最短路径上的点为初始节点开始采样.Jalali等人[14]提出了基于生成树的社交网络采样算法,首先随机选择一些节点作为种子节点,根据这些种子节点生成多个生成树,选择频繁度较高的边作为采样边.基于拓扑结构的采样算法虽然在一定程度上增加了采样的精确度,但是时空复杂度过高,只适合小规模的图或图集,当处理大规模单图时则时空开销大,无法有效处理.
2 基本概念
定义1. 子图同构[15].给定图G=(V,E,L),G′=(V′,E′,L′),V,V′表示节点集合,E,E′表示边集合以及L,L′表示节点和边的标签映射函数.如果G与G′存在这样的映射函数f:V→V′,满足:1)u∈V,L(u)=L′(f(u));2)(u,v)∈E,(f(u),f(v))∈E′且L(u,v)=L′(f(u),f(v)),则称G与G′为子图同构.
定义2. 频繁子图[16].给定图G和最小支持度MinSupport,Sup(G,S)表示子图S在图G中同构图的个数,当Sup(G,S)>MinSupport,S为G的一个频繁子图.
给定图G和最小支持度MinSupport,从图G中找出支持度大于MinSupport的所有子图的过程称为频繁子图挖掘.
在图1中,共存在9个子图:A-2-B,B-1-C,B-3-C,A-2-B-1-C,A-2-B-3-C,B-1-C-3-B,A-2-B-1-C-3-B,A-2-B-3-C-1-B,A-2-B-1-C-3-B-2-A,支持度分别为:2,1,1,1,1,1,1,1,1.当最小支持度为1时,共有9个频繁子图;当最小支持度为2时,共有1个频繁子图;当最小支持度为3时,则没有频繁子图.
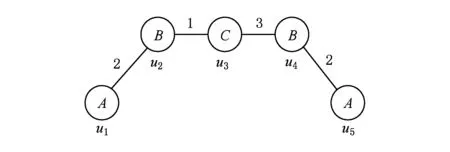
Fig. 1 The example of frequent subgraph图1 频繁子图挖掘样例图
定义3. 频繁边及其方差.给定一个边eu,且给定最小支持度MinSupport,当且仅当eu的支持度不小于最小支持度阈值时称边eu为频繁边,将频繁边的频繁度的方差定义为频繁边方差,在频繁子图挖掘过程中,当频繁边方差越大,图中频繁边的分布越不均匀,最终挖掘时间越长.
定义4. 边聚集系数.1条边的2个端点与其共同邻接点之间的另外2边所组成的三角环(边数为3的闭合回路)与可能包含该边的最大的三角环数之间的比值,公式如下:
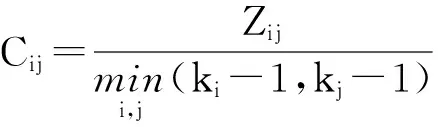
(1)
其中,ki,kj分别表示节点i和节点j的度,Zij表示网络中实际包含该边的三角环的个数.
3 基于频繁边的图采样
3.1 内存分布式计算框架——Spark
Spark[17]是UC Berkeley AMP Lab开源的类Hadoop通用的并行计算框架,Spark基于Hadoop MapReduce算法实现分布式计算,拥有Hadoop所具有的优点;但不同于Hadoop将Job中间输出和结果保存在HDFS,而将其直接保存在内存中,且Spark启用了弹性分布式数据集,除了能够提供交互式查询外,它还可以优化迭代工作负载.因此Spark能更好地适用于数据挖掘与机器学习等需要迭代的MapReduce的算法.其架构如图2所示:
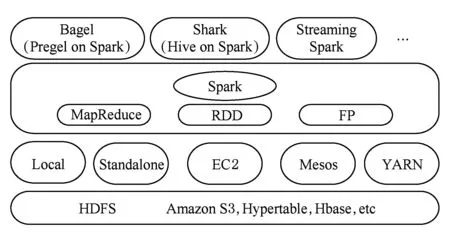
Fig. 2 The framework of Spark图2 Spark架构
3.2 基于频繁边的分布式图采样算法
在进行频繁子图挖掘时,频繁边的分布相对于节点的度更为重要,本文提出了基于随机跳和图感应的蒙特卡罗采样方法MSARI,首先根据频繁边的分布进行图采样.采样中增加随机跳转,在满足随机跳转概率后,对当前边和将要跳转边进行频繁度比较,当跳转边的频繁度小于当前边的频繁度,则跳转.从边eu跳转到边ev的概率如式(2)所示:
(2)
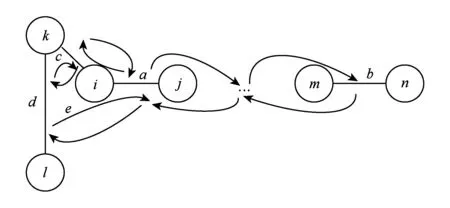
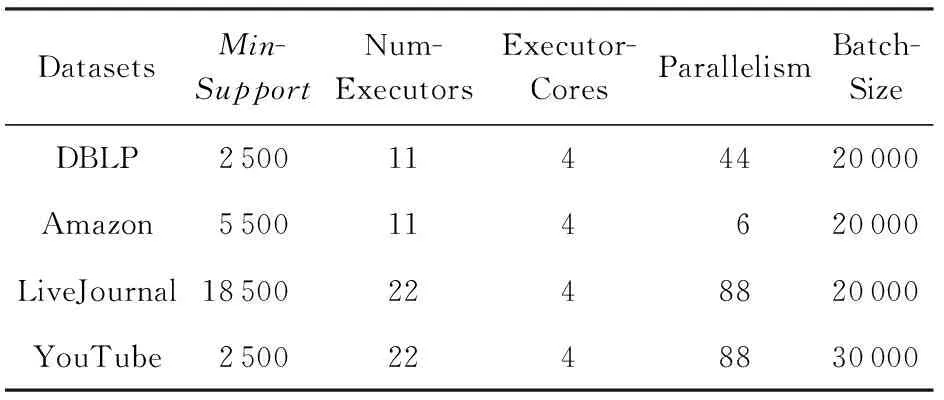
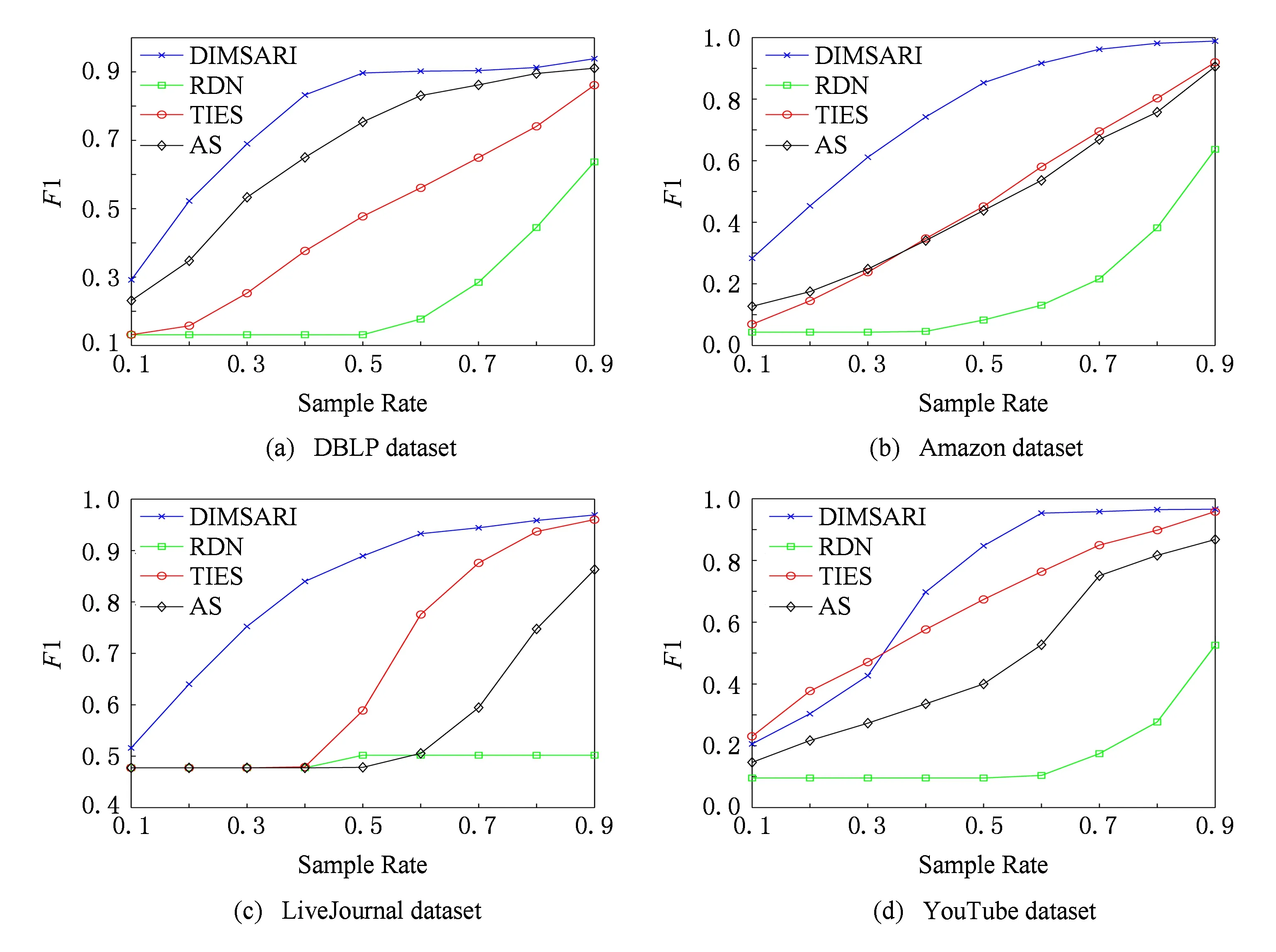
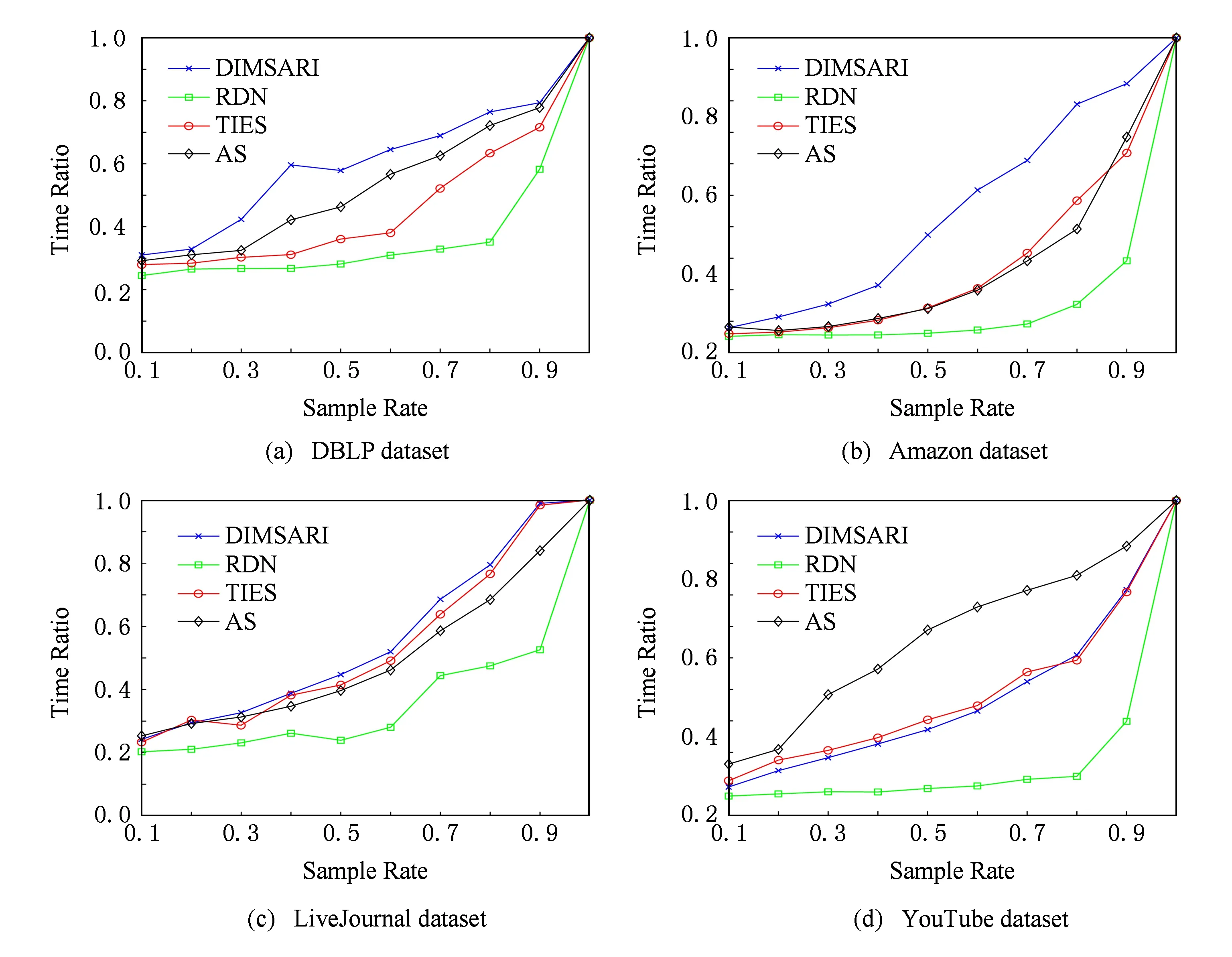
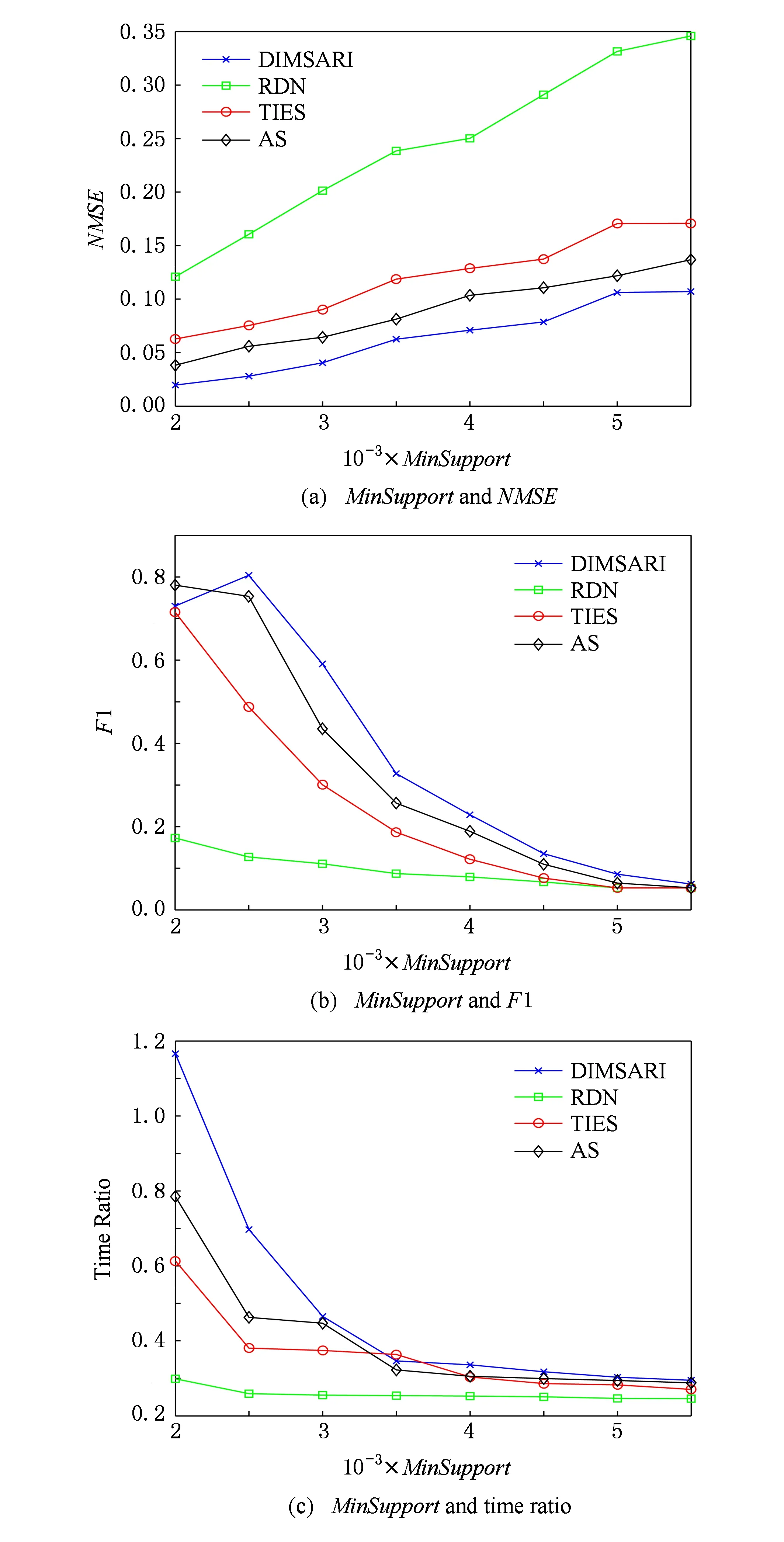
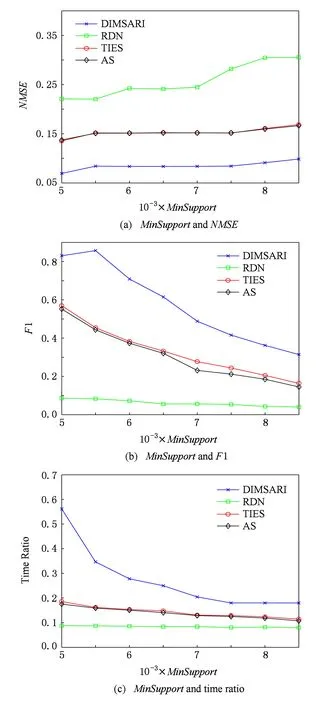
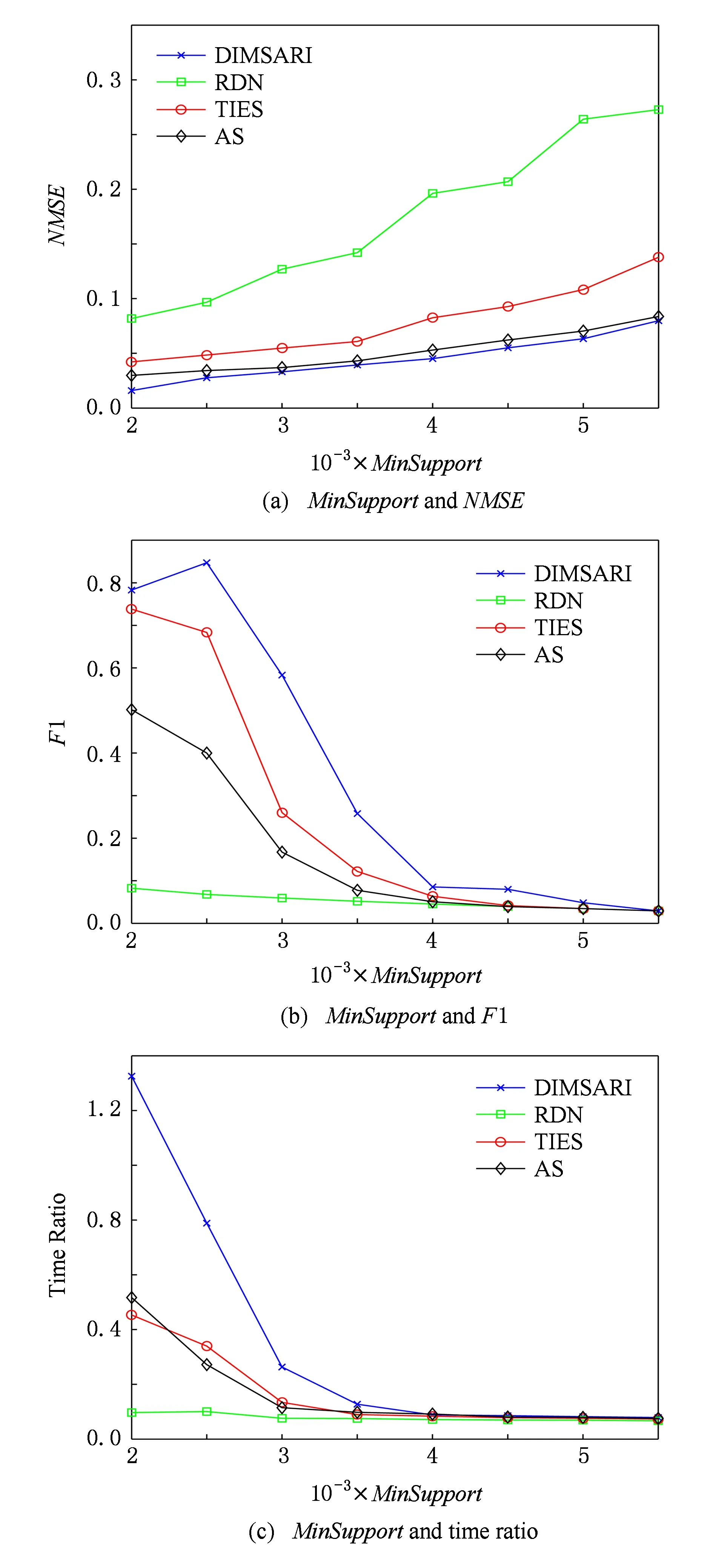
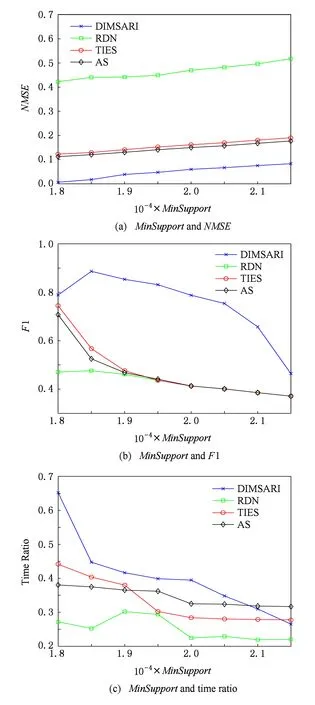
式(2)表示MSARI算法转移概率,蒙特卡洛算法根据节点的度转移,在采样的过程中对节点无偏性,跳转到各节点概率都满足1|V|,而MSARI算法根据边的频繁度进行转移,在采样的过程中按照频繁边进行采样,ev代表当前的采样边,eu代表将要扩展的采样边,且eu为ev的相邻边,f代表边的频繁度,当满足跳转概率后,对eu和ev的频繁度进行判断.当random(0,1) 最后,为了增加采样后的子图的连通性,提升采样后频繁子图的召回率,在初步采样结束之后进行图感应处理,采样后对原始图进行遍历,如果采样后子图的边的2个节点都被采样且原始图有边相连而采样后没有边相连,则将其边添加到子图上以增加子图的连通性. Fig. 3 The demo of graph induced operation图3 图感应操作演示 MSARI算法伪代码如下: 算法1. MSARI采样算法. 输入:待采样的图G、采样率R、随机跳转的概率p; 输出:采样之后的边sampleEdge. ①sampleCount=r×G.vertexs;*得到采样的数量* ②ev=random(G.edge);*从原图的节点 中随机取一条边* ③sampleSet=Set(ev);*采样后的集合* ④ whilesampleVertex.size ⑤ ifrandom(0,1) ⑥eu=random(G.edge);*原图的节 点中随机取一条边* ⑦ ifrandom(0,1) ⑧ev=eu; ⑨SampleSet.add(eu);*将eu添加到采样集合中* ⑩ end if 为了处理大规模单图,本文将MSARI算法扩展为分布式环境下的DIMSARI算法,由于需要多次迭代处理,Hadoop的MapReduce操作需要多次读取HDFS上的文件,时间开销大,并不适用,而Spark的RDD操作可以满足多次迭代要求,因此,实验使用的分布式平台为Spark,Partition是Spark的分区.DIMSARI算法步骤如下: 1) 使用节点分割策略进行原图的划分,将其划分为多个分区; 2) 在各自的分区上完成MSARI算法的采样工作; 3) 在各自分区采样完成的采样图的基础上进行图感应操作,增加连通性; 4) 将各自分区采样完成的采样图进行合并,形成单个采样图. 算法2. DIMSARI采样算法. 输入:待采样的图G、采样率r、随机跳转概率p; 输出:采样完成后子图Gsub. ①edgeFreqMap=getFrequentEdgeMap(G);*获取边的频繁度* ②sampleEdgeRdd=G.partitionBy(EdgePartition2D).map(edge(edge-FreqMap)).mapPartition{iter≥MSARI(iter,r,p)};*进行各个分区的MSARI采样* ③ returnnewGraph(SampleEdgeRdd).*返回采样后的图* 算法2中,行①对原始图进行过滤并获取边的频繁度;行②使用Graphx中的EdgePartition2D对原始图进行划分,根据边的频繁度获取图信息,并对每一个分区进行MSARI算法操作,得到各个分区结果;最后将总结果返回. 3.3 无偏性分析 MSARI算法在采样的过程中每一步只与当前边和其将要转移的边有关,因此,MSARI采样算法的过程可以抽象成一个Markov过程.其中,采样到的边eu为Markov过程的状态eu,从边eu到边ev的概率Pe u,ev表示为Markov过程的状态转移概率Pe u,ev.在时间T采样到边eu的概率等价于Markov过程中状态eu在时间T的状态分布.如果该Markov过程属于平稳分布,则当采样时间足够长,该Markov过程的状态分布将收敛至特定的平稳分布π=(πe 1,πe 2,…,πe |E|)T,其中|E|为原始图的边的个数.此概率分布π对应着采样算法对网络每条边的采样概率.当π服从均匀分布时,即πe 1=πe 2=…=πe |E|,该采样算法则是无偏的. 引理1. 如果原始连通图包含至少1个聚集系数不为0的边,且对任意2条边eu,ev,都有P{Pe v,eu>0|Pe u,ev>0}=1,则该原始图抽象出的Markov过程是遍历不可分的. Fig. 4 An example of Markov chain abstracted from sampling process图4 采样过程中抽象出的Markov链示例 可以看出,边i-a-j可以至多|E|-3步就可以到达图中任意边,即边i-a-j可以通过|E|-3-2n或|E|-3-2n-1次转移到达图中任意边,其中n表示一个非负整数.设he a,eb表示从边i-a-j到边m-b-n的最短转移次数.如果he a,eb=|E|-3-2n,边i-a-j可以在he a,eb步的基础上经过n+1个2跳回环i-a-j→i-c-k→i-a-j到达边m-b-n,即可以通过|E|-1步从边i-a-j转移到边m-b-n;当he a,eb=|E|-3-2n-1,边i-a-j可以在he a,eb步的基础上经过n个2跳回环i-a-j→i-c-k→i-a-j和一个3跳回环i-a-j→i-c-k→k-d-l→i-a-j到达边m-b-n,即可以通过|E|-1步从边i-a-j转移到边m-b-n. 因此,必有正整数N=2(|E|-1)使得从图4中的任一边出发,经过N步到达其他任意边(以边i-a-j为中转边).即对于从图4中抽象出的Markov链,存在正整数N≥1,使得该Markov链中任意2个边ea,ec,有Pe a,ec(n)≥0.这是Markov过程遍历不可分的充分必要条件[18],所以引理1得证. 证毕. 证明. 1) 必要性.设定一个平稳的Markov过程的状态转移概率矩阵P为 则该Markov过程的平稳分布π为 π=(πe 1,πe 2,…,πe |E|)T, 状态转移矩阵P和平稳分布π满足式(3): (3) 在采样过程中,πe u表示在采样过程中边eu的采样概率,即对于无偏采样,∀eu,ev∈E,有πe u=πe v=1|E|,代入式(3)中可得: (4) 2) 充分性.根据引理1,如果原始图中至少存在一个聚集系数不为0的边,在该网络中进行随机游走的采样过程可以抽象为一个遍历不可分的Markov过程.因此,该Markov过程是一个平稳过程且式(3)有且只有唯一解.可以得出πe u=πe v=1|E|是式(3)的一组解,综上所述,该解为方程组的唯一解,即该采样算法在采样时间足够长时对每一个节点的采样概率相等. 证毕. 证明. 1) 必要性.在节点i上,设定一个平稳的Markov过程的状态转移概率矩阵Pi为 则该Markov过程的平稳分布πi为 πi=(πe 1,πe 2,…,πe |Ei|)T. 状态转移矩阵Pi和平稳分布πi满足方程组: (5) 在采样过程中,πe i表示在采样过程中边ei的采样概率,对于无偏采样,∀ei,ej∈E,有πe i=πe j,代入式(5)可得: (6) 根据式(6)可得: (7) 2) 充分性.根据引理1,如果原始图中至少存在一个聚集系数不为0的边,则整个采样过程可以抽象为一个遍历不可分的Markov过程.因此,该Markov过程是一个平稳过程且式(5)有且只有唯一解,而πe u=πe v=1|E|是其中一个解,因此πe u=πe v=1|E|就是唯一解,即该采样算法在采样时间足够长时对每一个节点的采样概率相等. 证毕. 因此,该采样方法在分布式环境下具有无偏性. 3.4 频繁子图挖掘算法—FSMBUS 针对现有图的规模不断扩大,使用完整图用于频繁子图的挖掘时间和空间复杂度过高,使用DIMSARI算法采样后进行频繁子图挖掘,在保证准确率的前提下大大减少了算法的运行时间和空间复杂度.本文使用文献[19]的FSMBUS算法对采样后的子图和原始图分别进行频繁子图挖掘,通过对频繁子图F1值和NMSE比较,分析算法的有效性. 2015年严玉良等人[19]提出的基于Spark的大规模单图频繁子图挖掘算法FSMBUS,通过次优树构建并行计算的候选子图,在给定最小支持度后挖掘出所有满足条件的频繁子图,并利用非频繁检测和搜索顺序选择进行优化,并设计了一种名为Sorted-Greedy的轻量级数据划分方法.FSMBUS算法的主题框架包括数据准备阶段和挖掘阶段,挖掘阶段是算法的核心部分,将次优树按照广度优先搜索进行生长,并行计算每一层中CAM所表示的候选子图是否频繁,将不频繁的候选子图进行剪枝操作,剩余的候选子图继续生长,进入下一次迭代,直到候选子图都为非频繁子图算法停止. 3.4.1 数据准备阶段 数据准备阶段主要是进行频繁边的收集以及频繁子图数据集的初始化的工作. 当原始图输入到算法中时,根据最小支持度过滤非频繁边,将过滤后的边按照三元组(起始标签,边标签,目标标签)进行存储,将其作为次优树的第1层的频繁子图,同时使用频繁边RDD存储频繁边两边的节点集合,频繁边RDD作为扩展边的缓存. 3.4.2 挖掘阶段 挖掘阶段主要通过迭代的方式将所有的频繁子图计算出来,包括候选子图的生成、构建候选搜索数据域以及支持度的计算. 1) 候选子图的生成.第i次迭代由第i-1次迭代产生的频繁子图进行FFSM-Join和FFSM-Extend后产生候选子图. 2) 构建候选搜索数据域.使用增量的方式获取对应的搜索数据域,每个候选子图包含了父节点信息以及扩展边信息,当前候选子图的搜索数据域为父级子图的有效分配数据连接扩展边对应的有效分配数据. 3) 支持度的计算.对候选搜索数据域进行支持度的计算,采用启发式算法来进行搜索. 3.5 复杂度分析 原始图的节点个数为N,采样率为r.首先,使用蒙特卡罗算法进行采样,时间复杂度为O(r×N);然后,在蒙特卡罗算法的基础上增加了随机跳概率p,因此,时间复杂度变为p×O(r×N)+(1-p)×O(r×N);最后,增加了图感应操作,需要遍历原始图,找出采样后的子图丢失边,时间复杂度为O(N),因此总的时间复杂度为p×O(r×N)+(1-p)×O(r×N)+O(N),对采样后的子图进行频繁子图挖掘的时间复杂度在文献[19]中已经给出为O((n-2)×N3+n×τη×((1-θ)×N)n-1),因此总的时间复杂度为O(r×N)+O(N)+O((n-2)×N3+n×τη×((1-θ)×N)n-1). 实验使用普通PC机22台,其中1台主节点,剩余21台为从节点.每台PC机的配置相同:操作系统为Centos 6.5,CPU为Intel Core i5 2.4 GHz,8 GB内存,使用Scala 2.10.4开发,集群环境为建立在Hadoop2.2.0之上的Spark 1.2.0,jdk版本为1.7. 4.1 数据集和对比算法 实验数据集来自真实数据集SNAP[20],如表1所示: Table 1 The Description of Dataset 表1中,描述信息和相关处理如下: 1) DBLP(digital bibliography & library project).DBLP是计算机领域内对研究的成果以作者为核心的一个计算机类英文文献的集成数据库系统,按年代列出了作者的科研成果,包括国际期刊和会议等公开发表的论文.节点表示作者,节点的标签表示其所在的学术领域,边的标签为其作者之间的合作次数,为幂率分布数据集. 2) Amazon.亚马逊商城上商品信息,节点表示商品,边i-j表示购买商品i的同时购买商品j,节点标签表示商品ID,边标签表示商品被同时购买的次数.由于原始数据集上并不含有节点和边的标签,因此随机地对节点和边进行标签的添加,标签分布服从高斯分布,节点和边标签分别为5个和10个,为非幂率分布数据集. 3) LiveJournal.来自于LiveJournal社交网络,节点表示用户,标签表示用户ID,边表示用户之间有关系,标签表示用户之间的关系.由于原始数据集上并不含有节点和边的标签,因此随机地对节点和边进行标签的添加,标签分布服从高斯分布,节点和边标签分别为50个和5个,为幂率分布数据集. 4) YouTube.来自于谷歌旗下的视频分享网站,类似于一个社交网络,节点表示用户,标签表示用户ID,边表示用户之间有关系,标签表示用户之间的关系.由于原始数据集上并不含有节点和边的标签,因此随机地对节点和边进行标签的添加,标签分布服从高斯分布,节点和边标签分别为25个和5个,为非幂率分布数据集. 针对不同的数据集特点,在算法的运行过程中需要设置不同的参数使其能够运行,具体的参数设置如表2所示.表2中,MinSupport表示最小支持度,只有满足最小支持度的子图才会认为是频繁子图;Num-Executors表示执行的CPU数量;Executor-Cores表示执行核心数;Parallelism表示算法的并行程度;Batch-Size表示防止内存溢出,对任务进行了分片处理的分片大小. Table 2 Experiment Parameter Setting 为了评估DIMSARI算法的性能,实验部分选择了与下列算法进行对比,对比算法都改造为Spark平台下的算法,以保证实验运行环境的一致性. 1) RDN.是文献[2]的随机节点采样算法的进化版本,采样的过程中偏向于节点度比较高的节点,属于不均匀采样. 2) TIES.是在文献[11]的随机边采样的基础上增加了图感应操作,准确率得到了较大的提高. 3) AS.是文献[8]的MHRW算法和文献[9]随机跳算法的结合,可以有效地避免陷入局部区域,增加了非连通图处理. 4.2 度量指标 1) 归一化均方偏差(normalized mean squared error,NMSE) NMSE是一种常用的检验方法,主要用于检验采样后的子图节点的度与原始图节点的度的差异,定义如下: 其中,θ表示原始图的节点的度,θ′表示采样后子图节点的度.NMSE值越小,代表采样后的子图节点的分布与原始图越相似. 2) 准确率、召回率和F1值 Accuracy=HitsSampledCount, Recall=HitsOriginalCount, F1=2×Accuracy×Recall(Accuracy+Recall), 其中,Hits表示采样前和采样后频繁子图相同的数量,SampledCount表示采样后子图的频繁子图的数量,OriginalCount表示采样前原始图的频繁子图的数量. 准确率为采样前后频繁子图相同的数量与采样后子图的频繁子图的数量的比值,召回率为采样前后频繁子图相同的数量与采样前原始图的频繁子图的数量的比值,对准确率和召回率进行组合得到F1值,可以有效地评价结果的好坏. 4.3 采样前后的结构相似度评估 采样后的子图是否保持原图的结构可以评价采样结果的好坏,采样后的子图与原始图的节点的度的NMSE值对比结果在图5中给出,各数据集的参数设置如表2所示. 图5显示了不同的数据集下不同的采样率时各算法的NMSE值的大小.可以看出,不管在哪种数据集下,DIMSARI算法的NMSE值都是最小,说明使用DIMSARI算法对原图的结构保持最好;随着采样率的提高,NMSE值逐渐减小,满足采样越多,跟原图结构越相似的特点;AS算法性能次之,这是因为在采样时只考虑节点的度,没有考虑边的缺失,实验显示性能普遍低于DIMSARI算法;TIES算法在随机边采样的基础上增加了图感应操作,可以看出其结果与AS算法类似,随机边采样后边稀疏,NMSE值会很高,在此基础上增加了图感应操作,将丢失边补齐,使其取得不错的结果;而RDN算法根据节点的度进行采样,集中于采样节点度较高的节点,使其NMSE值较大,与原图结构相似性较低. Fig. 5 Sample Rate and NMSE图5 采样率与NMSE图 Fig. 6 Sample Rate and F1 score图6 采样率与F1值图 4.4 采样后频繁子图挖掘的性能评估 将本方法与对比采样方法用于频繁子图挖掘,挖掘方法均采用文献[18]的算法,F1值的结果如图6所示(各数据集的参数设置见表2). 图6显示在不同的数据集下DIMSARI与RDN,TIES,AS算法的对比,横坐标表示采样率的范围是0.1~0.9,纵坐标表示算法的F1值.从图6可以看出,DIMSARI算法在DBLP数据集、Amazon数据集、LiveJournal数据集中不同的采样率下F1值都是最高;在YouTube数据集上,在采样率低于0.3时被TIES算法短暂超越,此时采样率较低,采样后的子图构成的频繁子图个数少,但是随着采样率的提高,DIMSARI算法有明显的优势.图6中之所以出现直线,是因为进行频繁子图挖掘时设置最小的子图为边,因此根据最小支持度,每一个数据集都有一个固定的边集组成的频繁子图集合,频繁子图挖掘时将单个边进行边扩展,挖掘满足条件的频繁子图,后期不会出现直线. 对采样后的子图进行频繁子图挖掘,在保证准确性的前提下时间开销的实验结果如图7所示: Fig. 7 Sample rate and time ratio图7 采样率与时间比图 图7中横坐标表示采样率,纵坐标表示采样后子图进行频繁子图挖掘的时间与原始图进行频繁子图挖掘的时间的比值.从图7可以看出随着采样率的提高,先采样再进行频繁子图挖掘的时间不断增加;由于在AS算法的基础上增加了随机跳转判断以及图感应操作,使得DIMSARI算法的运行时间最长;而TIES算法和AS算法在大部分数据集上运行时间类似,比DIMSARI算法的运行时间短;RDN算法由随机节点采样增加了节点度的考虑,运行时间最短,但是其F1值最低,不能很好地满足采样后进行频繁子图挖掘. 4.5 不同最小支持度下算法性能评估 在采样率保持0.5不变的情况下,比较不同的最小支持度下进行采样后的子图与原始图的归一化均方偏差NMSE、采样后进行频繁子图挖掘的结果的F1值和运行时间,实验的结果如图8~11所示. Fig. 8 DBLP dataset图8 DBLP数据集 Fig. 9 Amazon dataset图9 Amazon数据集 Fig. 10 YouTube dataset图10 YouTube数据集 Fig. 11 LiveJournal dataset图11 LiveJournal数据集 图8~11显示4个真实数据集下NMSE,F1值和运行时间与最小支持度的关系.首先,比较最小支持度与NMSE的关系,随着最小支持度不断减小,NMSE值也减少,DIMSARI算法的NMSE值显著小于其他算法,而TIES和AS算法的NMSE比较相近,两者都次于DIMSARI算法,而RDN算法的NMSE值最大,说明RDN算法在采样后的子图结构与原始图差距最大,DIMSARI算法与原始图结构最相似.其次,比较最小支持度与F1值的关系,随着最小支持度不断减小,RDN,TIES,AS算法的F1值一直保持增长,而DIMSARI算法的F1值会有一个增加后减少的过程,原因在于对原始图进行频繁子图挖掘会给定一个最小支持度,一旦超过该支持度则原始图无法进行频繁子图挖掘,对原始图采样后虽然可以解决频繁子图挖掘操作,但是会挖掘出更多的子图,使得准确率降低从而导致F1值减少.最后,比较最小支持度与采样后进行频繁子图挖掘时间开销的关系,随着最小支持度不断减小,运行时间一直保持增加,由于DIMSARI算法在AS算法的基础上增加了随机跳转判断以及图感应操作,使得DIMSARI算法的运行时间比其他算法的运行时间长.从上面几个实验综合可以看出,虽然在相同的采样率和最小支持度下DIMSARI算法的运行时间最长,但是在达到相同的F1值的情况下,DIMSARI算法的运行时间最短;而RDN算法采样的是在随机节点采样的基础上增加了节点度的考虑,运行时间短,但是其F1值不能满足频繁子图挖掘需要. DIMSARI算法根据频繁边的分布进行采样,在采样后进行频繁子图挖掘,不管在幂率图上还是非幂率图上都取得不错的结果.TIES算法在随机边采样的基础上增加了图感应操作,AS算法是在MHRW算法的基础上增加了随机跳算法,此2种算法运行结果较为满意,但都次于DIMSARI算法.RDN算法由于采用的是随机节点采样,虽然在采样的过程中根据节点度的信息进行采样,但是由于其采样时有偏性,使其在进行频繁子图挖掘时效果最差. 本文提出了一种Spark环境下基于频繁边的大规模大图的采样算法——DIMSARI,该算法在蒙特卡罗算法的基础上增加了根据频繁边进行随机跳的操作,在跳转时考虑边的频繁度选择是否跳转,并对采样后的结果进行了图感应操作,一定程度上增加了算法的有效性.实验通过对采样后的子图的节点的度与原始图节点的度的差异以及采样后的子图进行频繁子图挖掘的结果与原始图进行频繁子图挖掘的结果进行了准确性和时间对比,显示该算法比现有算法更加准确和有效. 本文针对频繁子图挖掘进行了基于频繁边的采样算法研究,后期工作可以将其扩展到子图同构等图算法工作中来提高算法的运行效率. [1]Facebook. Facebook annual reports[EBOL]. 2015 [2016-04-08]. http:investor.fb.comannuals.cfm [2]Wang Dong, Li Zhenyu, Xie Gaogang. Unbiased sampling technologies on online social network[J]. Journal of Computer Research and Development, 2016, 53(5): 949-967 (in Chinese)(王栋, 李振宇, 谢高岗. 在线社会网络无偏采样技术[J]. 计算机研究与发展, 2016, 53(5): 949-967) [3]Leskovec J, Faloutsos C. Sampling from large graphs[C]Proc of the 12th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2006: 631-636 [4]Ahmed N, Neville J, Kompella R R. Network sampling via edge-based node selection with graph induction[EBOL]. 2011[2017-02-09]. https:www.researchgate.netpublica-tion254639513 [5]Blagus N, Subelj L, BajecM. Improving the accuracy of network sampling with subgraph induction[JOL]. Physica A, 2014[2016-10-21]. http:lpt.fri.uni-lj.sifileslovroresearchpa-persssi.pdf [6]Lovász L, Lov L, Erdos O P. Random walks on graphs: A survey[J]. Combinatorics, 1996, 8(4): 1-46 [7]Leskovec J, Kleinberg J, Faloutsos C. Graphs over time: Densification laws, shrinking diameters and possible explanations[C]Proc of the 11th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2005: 177-187 [8]Ahn Y Y, Han S, Kwak H, et al. Analysis of topological characteristics of huge online social networking services[C]Proc of the 16th Int Conf on World Wide Web. New York: ACM, 2007: 835-844 [9]Gjoka M, Kurant M, Butts C T, et al. Walking in Facebook: A case study of unbiased sampling of OSNs[C]Proc of the 30th IEEE Int Conf on Computer Communications. Los Alamitos, CA: IEEE Computer Society, 2011: 1-9 [10]Jin Long, Chen Yang, Hui Pan, et al. Albatross sampling: Robust and effective hybrid vertex sampling for social graphs[C]Proc of the 3rd ACM Int Workshop on MobiArch. New York: ACM, 2011: 11-16 [11]Yoon S H, Kim K N, Hong J, et al. A community-based sampling method using DPL for online social networks[J]. Information Sciences, 2011, 306: 53-69 [12]Du Xiaolin, Ye Yunming, Li Yueping, et al. A new relational networks sampling algorithm using topologically divided stratums[J]. Advanced Science and Technology Letters, 2014, 48: 108-119 [13]Rezvanian A, Meybodi M R. Sampling social networks using shortest paths[J]. Physica A: Statistical Mechanics & Its Applications, 2015, 424: 254-268 [14]Jalali Z S, Rezvanian A, Meybodi M R. Social network sampling using spanning trees[J]. International Journal of Modern Physics C, 2015, 27(5): 1-20 [15]Ullmann J R. An algorithm for subgraph isomorphism[J]. Journal of the ACM, 1976, 23(1): 31-42 [16]Holder L B, Cook D J, Djoko S. Substructure discovery in the subdue system[C]Proc of the Workshop on Knowledge Discovery in Databases. Menlo Park, CA: AAAI, 1994: 169-180 [18]Nummelin E. General Irreducible Markov Chains and Nonneigative Operators[M]. Cambridge, UK: Cambridge University Press, 2004 [19]Yan Yuliang, Dong Yihong, He Xianmang, et al. FSMBUS: A frequent subgraph mining algorithm in single large-scale graph using Spark[J]. Journal of Computer Research and Development, 2015, 52(8): 1768-1783 (in Chinese)(严玉良, 董一鸿, 何贤芒, 等. FSMBUS: 一种基于Spark的大规模频繁子图挖掘算法[J]. 计算机研究与发展, 2015, 52(8): 1768- 1783) [20]Standford University. SNAP[EBOL]. [2016-05-23]. http:snap.stanford.edusnappy Li Longyang, born in 1991. Master from the Faculty of Information Science and Engineering, Ningbo University. His main research interests include data mining and machine learning. Dong Yihong, born in 1969. PhD, professor and master supervisor in the Faculty of Information Science and Engineering, Ningbo University. His main research interests include big data, data mining and artificial intelligence. Yan Yuliang, born in 1990. Master from the Faculty of Information Science and Engineering, Ningbo University. His main research interests include graph mining, cloud computing and machine learning. Chen Huahui, born in 1964. PhD, professor. Member of CCF. His main research interests include data streams and massive data processing (chenhuahui@nbu.edu.cn). Qian Jiangbo, born in 1974. PhD, professor. Member of CCF. His main research interests include data management, streaming data processing, multidimensional indexing and query optimization (qianjb@163.com). A Sampling Algorithm Based on Frequent Edges in Single Large-Scale Graph Under Spark Li Longyang, Dong Yihong, Yan Yuliang, Chen Huahui, and Qian Jiangbo (FacultyofElectricalEngineeringandComputerScience,NingboUniversity,Ningbo,Zhejiang315211) With the popularity of social networks, the demand for its frequent subgraph mining becomes more intense. With the arrival of the era of big data, social networks have been expanding and frequent subgraph mining becomes increasingly difficult. In fact, it does not require to mine frequent subgraphs exactly in application, so sampling methods are adopted to improve the efficiency of mining frequent subgraphs under certain accuracy. Most existing sampling algorithms are not fit for frequent subgraph mining because they use vertex transfer or compute the topology of the original graph first which will take a lot of time. In this paper, we propose a new sampling algorithm named DIMSARI (distributed Monte Carlo sampling algorithm based on random jump and graph induction) based on frequent edge, and it runs on a distributed framework named Spark. This algorithm is created on the basis of the Monte Carlo algorithm meanwhile adding random jump. The results are added by subgraph induction step to promote the accuracy of the algorithm and prove that the algorithm is unbiased. The experiments show that the accuracy of frequent subgraph mining using DIMSARI algorithm has been greatly improved and at the same time the proposed algorithm only spends a little more time than other algorithms. The apex of sampling at different sampling rates after subgraphs has maintained a lower normalized mean square error. sample; frequent subgraph; single large-scale graph; frequent edge; Spark 2016-07-27; 2017-03-07 国家自然科学基金项目(61572266,61472194);浙江省自然科学基金项目(Y16F020003);宁波市自然科学基金项目(2017A610114) This work was supported by the National Natural Science Foundation of China (61572266, 61472194), the Natural Science Foundation of Zhejiang Province of China (Y16F020003), and the Natural Science Foundation of Ningbo of China (2017A610114). 董一鸿(dongyihong@nbu.edu.cn) TP301




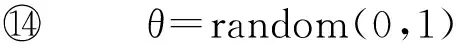
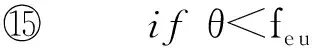









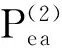
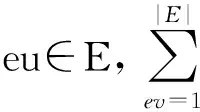


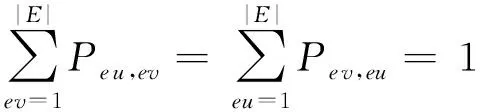
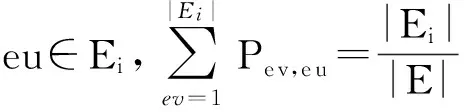
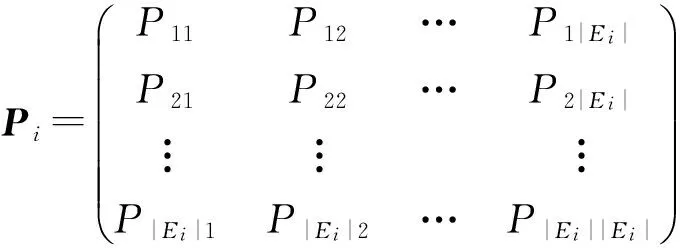
4 实验结果与分析
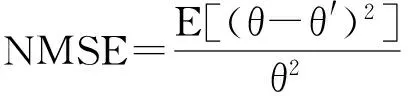

5 总 结





