多种风险下研发项目投资决策博弈分析

多种风险下研发项目投资决策博弈分析

曹博洋，姜明辉

(哈尔滨工业大学管理学院，黑龙江哈尔滨150001)

摘要：研发项目代表了高新技术企业的核心竞争力，但是其投资和研发的过程所包含的多种风险可能会造成企业经济上的损失。为了保证竞争优势和收益最大化，企业投资前需要对项目的估值非常的精确，以便在竞争中做出最优投资决策。本文以市场中的两个竞争性企业为例，利用欧式复合期权理论与博弈论，量化了技术风险、商业风险和突发风险等不确定性，在经过了信息披露过程之后，分析了市场中企业自身和竞争者的投资决策，建立相应的研发项目投资决策数学模型，对企业的研发项目投资时机和决策收益进行评估，通过博弈得到纳什均衡下的企业最优投资决策。

关键词：投资决策收益；最优决策；实物期权；博弈；研发项目；风险

收稿日期：2014-06-23

基金项目：国家自然科学基金资助项目(70871030)

作者简介：曹博洋(1982-)，男，北京人，博士研究生，研究方向为风险管理和实物期权；姜明辉(1967-)，男，黑龙江牡丹江人，教授，博士生导师，研究方向为实物期权、产业经济和个人信用评估。

中图分类号：F224. 32文章标识码：A

R&D Project Investment Decision Game Analysis Under A Variety of Risks

CAO Bo-yang, JIANG Ming-hui

(SchoolofEconomicsandManagement,HarbinInstituteofTechnology,Haerbin150001,China)

Abstract:R&D projects represent the core competitiveness of the high-tech enterprises, and there are a variety of risks in investment and research process. In order to keep competitive advantages and maximize the benefits, it needs to be very accurate in valuation of the projects for the optimal investment decisions in the competition before investment. By utilizing the European option value and game theory, quantified technical risk, economic risk and sudden risks, and combined with the jump-diffusion process and information revelation process, after analyzing investment decisions of enterprises themselves and competitors in the market, this paper establishes the corresponding R&D projects investment decision payoff mathematics model which can assess the timing and payoffs of the investment for two enterprises and obtain the optimal investment decisions after Nash equilibrium.

Key words:investment decision-making payoffs; optimal investment decisions; real options; game; R&D projects; risks

0引言

在全球化经济环境下，企业竞争焦点已经从产品阶段前移至研发阶段，因此企业未来的市场地位很大程度上是由于今天产生的竞争性投资机会所决定。对于研发项目来说，风险来自于外部市场波动性、项目本身所具有的复杂性、企业自身的研发能力和整体实力有限性，而经济危机和政治因素也都可以为研发项目带来突发性的风险。由于这些风险的存在，投资者预先无法确定具体的投资时机，导致研发项目收益达不到预期目标，因此准确地分析研发项目的投资决策对于企业的决策者来说变得尤为重要。

典型的研发项目投资具有：高风险性、不可逆性、可延迟性和阶段性。研发项目投资可以出现在很多类型的企业中，例如在生物医药企业中，许多新型医药在无现金流出的情况下，经过很多年的实验和测试，药品才能上市。根据传统的投资决策方法，如NPV(Net Present Value)方法，单纯依靠对现金流的计算无法反映研发项目投资决策的多种风险，因此经常低估并错误地拒绝有价值的投资机会，导致研发项目投资不足和企业竞争优势地位受到损失。然而根据商业经验，这类的投资机会显然是有价值的。实物期权理论作为金融期权理论在实物投资领域上的扩展，能够充分考虑风险的价值，并认为拥有在未来某时间段内进行投资或放弃投资的权利是有价值的，这能够恰当地反映投资所具有的策略柔性，从而可以作为风险分析与管理决策工具，用于实物资产定价以及投资策略的分析与评估。当内在或外在条件的变化不利于投资时，企业可以选择放弃该投资机会，其所损失的不过是不可逆的投资成本。等待而不立即进行投资的研发项目期权价值主要表现在，随着相关研发项目投资风险信息的逐步揭示，企业可以根据其投资战略需要而进行积极的研发项目投资管理，从而把握有利的投资机会。相比于普通项目， 研发项目还具有明显的阶段性特征，每个阶段有明确的阶段目标和工作任务，并且每个阶段任务的开始都和上一个阶段的工作成果相关联。研发项目投资决策和实物期权理论的结合可将研发项目的投资机会视为一个分阶段的、持续受投资环境条件变化影响的动态过程，并可以把整个投资分解为数个决策点，在每一个点上决策者可以根据变化的环境进行决策，其中企业决策者处于相对主动的地位。

当企业在竞争的市场条件下进行投资对，由于竞争各方的收益是相互牵制的，因此必须在投资决策过程中研究自身的竞争优势，以及在之后过程中竞争者的投资决策和竞争者进入后的对企业自身产生的影响。运用期权博弈的方法可以对项目投资时机进行战略性的选择，并且可以实现竞争与风险双重情形下的企业收益最大化目标，因此逐渐成为研发项目投资决策评价的新兴适用方法，备受国内外研究者关注。

Margrabe[1]定义了实物期权中的期权是这样一种特殊的合约，它赋予持有者在给定的期限内，以一种风险资产(交付性资产)交换另一种风险资产(期权性资产)的权利。McDonald 和 Siegel[2]模型评估了有分红行为的欧式期权，给出了期权的一个应用。Armada等[3]和Paxson[4]修正了Carr[5]的美式期权模型，在不增加过多数学计算的同时能计算出更精确的美式期权价值。Pennings和Sereno[6]把复合实物期权里加入了跳跃的因素，能够对突发风险进行评估，但是对研发项目中的其他风险没有讨论。Ghosh 和Troutt[7]发展了更复杂的多阶段复合式期权的模型，但是对于应用于实际还有很大距离。Thijssen等[8]仅定性研究了不确定性条件下的投资决策博弈。Martzoukos和Zacharias[9]研究了企业的溢出效应，一个企业研发项目的期权价值和投资决策受到其他企业研发成功与否的影响。Koussis等[10]对研发项目中的跳跃进行估值，并发现有高频率的竞争威胁并有较低波动率的项目价值更大。

在国内，用实物期权的方法进行投资决策分析成为最新的研究热点，使得期权持有者能够在软件业、生物制药业、以及石油工业等的研发项目中制定更好的决策来减低风险。冯晨娇， 刘维奇[11]利用不同的风险波动率和多阶段的复合期权对研发项目进行简单的计算。田季员等[12]建立了基于跳跃-扩散过程的研发项目投资决策模型，并对各参数进行了灵敏度分析。夏轶群， 陈俊芳[13]对研发项目投资时机的期权进行博弈找到将投资临界点，但只进行了定性分析。陈涛等[14]对软件的开发过程运用复合实物期权模型评估，很好的刻画了风险驱动的特征。杨金强和杨招军[15]通过蒙特卡洛模拟， 给出了投资者在完全信息和部分信息下的动态决策差异。谷晓燕等[16]分析了研发项目寿命期内面临的多种风险对研发项目潜在现金流的影响， 并重点研究了一些重点参数对项目价值的影响，但对于项目价值本身并未讨论。张新华等[17]对实物期权模型求解基础上进行了数值仿真分析来进行投资决策。何沐文等[18]建立基于多随机变量的自然资源开发项目实物期权投资评价模型，并应用Black-Scholes简单欧式期权结合鞅过程给出了模型的解析解。吴崇，胡汉辉[19]构建了不完全竞争市场的投资策略决策模型，根据均衡定性分析，研究了先后动优势以及内外生环境不确定性对企业间投资时机决策的影响。

目前，国内外研发项目投资决策理论的研究很多还只集中在对实物期权参数的定性分析和微分方程的推导上，并未把期权价值应用在企业对研发项目投资决策中，这对于现实中企业投资决策的帮助有限。由于实物期权的金融属性决定其本身是可以进行买卖的，因此在研发项目的投资以及转让和收购中，都需要量化的期权价值作为参考。而实物期权方法在不考虑其他市场参与者战略影响的情况下，解决了研发项目价值量化的问题，但是对于竞争者的存在和多种风险导致的风险估值不足，往往造成企业对研发项目价值和收益的计算不准确。本文站在企业投资的角度，一方面考虑市场中竞争者所带来影响的同时，另一方面对研发项目的多种风险进行量化分析和评估，并根据企业可能做出的投资决策，构建了多种不确定条件下的研发项目投资决策模型，来得到更加精确的实物期权价值和量化的投资决策收益，最后通过博弈论与实物期权理论的结合解决了竞争者行为和多种风险影响下的企业最优投资决策问题。

1研发项目投资决策基本模型

1.1基于欧式期权的研发项目投资决策模型

根据Margrabe[1]定义，欧式期权持有者可在T时刻以资产I交换资产V，而在研发项目中的解释就是在时刻T投资I得到了项目价值V，这个投资机会可以被作为欧式期权。Geske[20]推导了欧式期权价值模型，刻画了经济风险较高的研发项目价值。假定V和I都遵循几何布朗运动，欧式期权模型为：

s=VN1(d1(K,T))-Ie-rTN1(d2(K,T))

(1)

考虑到研发项目投资可以分阶段， 而每个阶段之间是因果的关系，并且互相嵌套，因此对研发项目估值时可以应用Carr[5]与Paxon[4]推导的两阶段复合欧式期权模型：

(2)

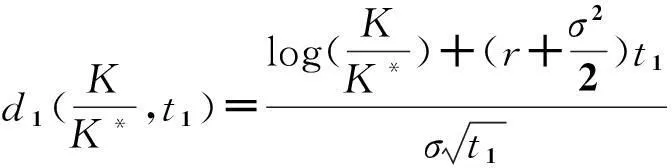
1.2包含跳跃-扩散过程的研发项目投资决策模型

在竞争性的研发项目投资环境中，项目的期权价值取决于多种来源的不确定性，如突发风险、经济风险和技术风险，这些因素会影响到各竞争中的企业收益和投资决策的制定。突发风险可用跳跃-扩散过程来描述。较早研究实物期权跳跃-扩散过程的是Merton[21]，其认为跳跃-扩散过程在研发项目中主要有两个不确定性的来源：扩散风险σdzt，包括正的和负的随机波动；突发事件dqt，主要描述了市场价值V的突然增加或减少。平均来说，在时间间隔[0,t]中有λt次跳跃，且跳跃的次数是独立于跳跃的大小，也独立于其他的不确定性。对于研发项目投资，更适合采用简化的跳跃-扩散过程模型，在时间间隔[0,t]中的跳跃次数既可以为0，也可为1，跳跃-扩散模型为：

(3)

其中μ为对项目的预期收益率，zt是一个标准的布朗运动过程，φ是泊松随机变量，用来描述跳跃过程。Pennings和Sereno[6]认为跳跃过程导致两个结果，一种是有价值，一种价值为0，可表示为：

假定企业是风险中性的，在未来任何时刻的项目价值都有这两种可能的情况，而该项目的最终价值应为这两种可能性下的期望值的和：

E=E[Vt(nt=1)]+E[Vt(nt=0)]=0+Ve(r+λ)t=Ve(r+λ)t

(4)

在欧式期权中，研发项目在时刻T的收益为max{Vt-I,0}，本文把欧式期权价值与跳跃到零的风险问题的计算简化为欧式期权价值与折现率问题的计算：

(5)

由此可得欧式期权定价模型为：

s(V,I,T) =e-λT(VeλTN1(d1(K,T))-Ie-rTN1(d2(K,T)))

=VN1(d1(K,T))-Ie-(r+λ)TN1(d2(K,T))

(6)

同样，本文把复合欧式期权计算归结为：c(s(V,I,T),I1,t1)=e-rt1e-λt1E[max{s(V,I,T)-I1,0}]。

由此可得包含了跳跃-扩散过程的两阶段复合期权模型：

(7)

2基于竞争性的研发项目投资决策收益分析

当企业在竞争的市场条件下进行投资时，由于竞争各方的收益是相互牵制的，因此必须在投资决策过程中研究企业自身的竞争优势和竞争者的行为，以及在之后过程中的竞争性行为对企业自身和其他竞争者产生的影响。在研发项目动态竞争中，市场上的竞争者通常可分为先进入市场的先行者企业和后进入市场的跟随者企业，跟随者虽然常常跟随在先行者后面进行决策，但是并不代表先行者无往不利。反而跟随者由于拥有先行者的研发信息披露，最终赢得市场的例子并不少见。由于整个市场的大小在一定时间内固定的，跟随者的进入，对先行者的收益是有影响的，因此作为先行者在进行投资决策时也要充分考虑到跟随者可能采取的决策，这就需要企业在制定研发项目投资决策时对所有可能的决策收益和竞争者的收益进行评估，并通过博弈找到纳什均衡，从而得到最优决策。

在研发项目投资过程中，除了经济危机一类的突发风险，通常含有的其他风险有：经济风险(如无风险利率r和市场波动率σ的变化)，和技术风险(用研发项目的研发成功率来描述)。假定存在两个竞争对手：企业A和企业B，研发成功率分别用q和p来表示。基于品牌，研发能力等的不同，设定企业A为研发和市场中的优势企业，企业B则为劣势企业，因此q>p。

本文规定先行者在t0时刻对研发项目投资，早于跟随者企业，两个企业的启动投资I1和市场化的投资I是一样的。但是两个企业所占市场份额不同，先行者企业占α，跟随者企业占1-α，且α>0.5。这里隐含的条件是两个企业占据整个市场成为双寡头垄断，但是现实中的竞争者很可能高于两个，会有几个先行者企业一起投资，也会有几个跟随者在等待，可以把这些同质的先行者企业简化成一个先行者作为替代，同样把其他跟随者企业看作一个跟随者来简化分析和计算。

根据欧式期权的定义，所有的决策点必须是固定的，因此企业所有的投资要在决策点t0时刻就定下来，这两个企业此时面临的决策为：是要进行在t0时刻的研发项目抢先投资，还是推迟到t1时刻投资，这就需要对所有可能的投资决策的收益进行计算和分析。由于在t0时刻和t1时刻都不投资相当于放弃项目，导致实物期权价值为零，本文不做研究，因此本文考虑了企业可能会做的四种投资决策：在t0时刻抢先投资成为先行者；推迟到t1时刻投资成为跟随者；与另一个企业t0时共同抢先投资；或者与另一个企业在t0时等待时机，再在t1时刻共同投资。

2.1任意一个企业抢先投资时的先行者收益

如果企业A作为先行者在t0时刻抢先投资研发项目，假定这时候跟随者企业B决定等待。在这个情况下，先行者企业A占有整个市场价值V的α，期权价值为s(αV,I,T)。Pennings和Sereno[6]对收益的计算为期权价值减去t0时刻投资，由此可知进行商业化投资I的必要条件是期权价值s(αV,I,τ)要高于I1的价值，只有这样才会产生收益。结合跳跃-扩散过程和研发成功率q之后，本文得到t0时刻企业A收益为：

LA(V,I)=qs(αV,I,T)-I1=q(αVN1(d1(K,T))-Ie-(r+λ)TN1(d2(K,T)))-I1

(8)

类似的，如果劣势企业B为先行者去投资研发项目，企业A为跟随者选择等待，企业B的先行者收益为：

LB(V,I)=ps(αV,I,T)-I1=p(αVN1(d1(K,T))-Ie-(r+λ)TN1(d2(K,T)))-I1

(9)

2.2观望先行者的研发信息披露再进行投资的跟随者收益

先行者第一个进入市场，会在市场上占据优势的同时对跟随者投资产生正外部性，这导致跟随者投资决策收益部分取决于先行者技术开发的信息披露程度，因此信息披露是一个影响跟随者最优投资决策的重要因素。研发成功率与信息披露之间的关系可以引入两个伯努利分布：

假设优势企业A作为先行者，在经过信息披露之后，如果先行者的研发项目研发是成功的，跟随者企业B的研发成功率p转化为正的信息披露时的p+；如果先行者失败了，此时的p转化为负的信息披露时的p-。根据Dias[23]对信息披露ρ(A,B)的计算可以得出：

p+=prob[A=1/B=1]=p(1-ρ(A,B))+ρ(A,B),p-=prob[A=1/B=0]=p(1-ρ(A,B))

(10)

同样，如果劣势企业B作为先行者，企业A的研发成功率可以转化为：

q+=prob[B=1/A=1]=q(1-ρ(A,B))+ρ(A,B),q-=prob[B=1/A=0]=q(1-ρ(A,B))

(11)

其中

(12)

设定两企业对项目的研发时间相同，则跟随者企业期权到期时间为T+t1。如果企业A作为先行者的研发项目投资是成功的，那么跟随者的研发项目投资成功率为p+。在投资I1之后，跟随者占据了全部市场的1-α份额，持有期权s((1-α)V,I,τ)。因此跟随者在t0时刻的收益为t1时刻到期的期权，执行价格为期权s((1-α)V,I,τ)。到期时刻t1，通过正信息披露的期权为：

c(p+)=c(p+s((1-α)V,I,(T+t1)),I1,t1)

(13)

通过公式(7)，本文把正信息披露的研发成功率与复合期权结合，可以得到：

(14)

(15)

在先行者的研发失败的情况下，本文可得到负的信息披露的期权价值：

(16)

(17)

如果企业A作为先行者成功率为q，跟随者企业B取得c(p+)，如果先行者失败概率为1-q，跟随者取得c(p-)作为期权。因此，本文得到t0时刻包含跳跃-扩散和信息披露过程的跟随者的企业B收益：

GB(V,I)=qc(p+)+(1-q)c(p-)

(18)

同样可得作为跟随者的企业A收益：

GA(V,I)=pc(q+)+(1-p)c(q-)

(19)

2.3两个企业同时抢先投资的收益

如果在t0时刻企业A和B决定同时投资研发项目，则此时没有信息披露，这使得ρ(A,B)=0，这使得p=p+=p-，q=q+=q-。本文可以设企业A和企业B可以获取到相同比例的市场，即α=0.5。由于两个企业对研发项目投资相同，因此企业A与企业B各自拥有期权s(0.5V,I,T)。根据公式(6)，本文可以得出同时在t0时刻投资研发项目时，包含跳跃-扩散过程和研发成功概率的企业A和企业B的收益分别为：

TA(V,I)=qs(0.5V,I,T)-I1=q(0.5VN1(d1(K,T))-Ie-(r+λ)TN1(d2(K,T)))-I1

(20)

TB(V,I)=ps(0.5V,I,T)-I1=p(0.5VN1(d1(K,T))-Ie-(r+λ)TN1(d2(K,T)))-I1

(21)

2.4两个企业等待市场时机再同时投资的收益

同样，如果在t0时刻两个企业都决定推迟他们的研发项目投资，此时也没有信息披露。两个企业期权到期时间同为T+t1，并且两个企业市场占有率也相等。在时刻t0投资I1之后，企业A或企业B拥有的期权为s(0.5V,I,τ)。根据公式(7)，在t0时刻，本文得到包含跳跃-扩散过程和研发成功率时，先等待市场时机再共同投资的两个企业中的企业A的收益为：

DA(V,I)=c(qs(0.5V,I,(T+t1)),I1,t1)

(22)

(23)

同理可得企业B收益为：

(24)

(25)

2.5决策收益分析

由此可得市场价值的四个临界值V1、V2、V3和V4，通过这四个临界值得到五个区间范围，每个区间中的最优决策都不相同，通过博弈企业可以得到不同市场价值下的研发项目最优投资决策。

3算例

3.1参数设置和结果分析

本文使用一个算例来讨论优势企业A和劣势企业B的投资决策收益。可以设：

先行者企业市场占有的比例高于跟随者，即α=0.60。在t0或者t1时刻进行的所有投资都遵循布朗运动，对下一阶段商业化投资为I=400000，在研发项目初始时刻的启动投资为I1=150000。V和I的波动率为σv=0.90,σi=0.23；变化系数ρvj=0.15。T表示项目的进行时间，采用T=3年。跟随者需要6个月来了解先行者的状态和结果，及收到信息披露，则t1=0.5年。无风险利率为r=0.05。跳跃系数为λ=0.076。最后优势企业A比B拥有更高研发成功率去做研发项目，企业A的研发成功率为q=0.60，企业B的研发成功率p=0.55，且先行者企业研发成功后的信息披露为ρ(A,B)=0.70 。

根据之前的决策收益分析，可以得到表1中的市场价值的临界值，由此可计算出如表2中的优势企业A和劣势企业B的投资决策收益。

表1　市场价值临界值

表2　企业 A和企业 B的投资决策收益

由图1和图2可见，当V为任意取值时，无论是优势企业还是劣势企业，某一个决策的收益并不会一直高于其他三个决策的收益。由于市场价值增加，所有决策的收益都会增加，而最优投资决策也会随之改变。从图中还可以看到V值有临界值，也就是图中曲线的交点，这时两个决策的收益相同，如V=9284010时，企业A在t0时刻作为先行者和与企业B在t1时刻共同投资的收益同为814374，也就意味着此时企业A拥有两个收益相同的最优投资决策。在竞争的市场中，企业A的最优决策还受到竞争者企业B的影响，这就需要对该条件下的两个企业收益进行博弈分析，根据纳什均衡得出竞争中的企业最优投资决策。

图1　企业A投资决策收益曲线　 　图2　企业B投资决策收益曲线

3.2博弈分析

实物期权博弈分析的主要包括两个方面：一是期权博弈的价值分析， 二是期权博弈的决策选择。利用表2中企业A和企业B在四个临界值构成的区间中的取值为例，进行博弈分析以得到该区间内企业的最优投资决策。

表3　市场价值为9000000时企业 A与企业 B决策收益

当V=9000000时企业A与企业B的投资决策收益如表3所示，若一个企业为市场中的先行者时，另一个企业可以选择同为先行者，这表示企业A和企业B在t0时刻共同抢先投资；或者另一个企业作为跟随者。若一个企业选择作为跟随者时，另一个企业可以选择作为先行者；或者另一个企业作为跟随者，这表示企业A和企业B都在t0时刻等待，而在t1时刻进行投资。从表3中可以得到企业A和企业B的投资决策矩阵分别为：

这是一个非合作的双矩阵博弈，对A和B的元素进行标号，得到：

其中a22和b22都有标号，因此企业A和企业B在V=9000000时的纳什平衡点为：(757524，641070)，这就表示在V=900000时的最优决策为企业A和企业B都在t0时刻等待，而在t1时刻进行投资。由此，可以得到V值在5个区间下的纳什均衡及最优决策：

V=9000000时，V

V=9500000时，V1DA，LB

V=10000000时，V2DA，LB>DB，TA

V=12000000时，V3DA，LB>DB，TA>GA，TB

V=14000000时，V>V4，且：LA>DA，LB>DB，TA>GA，TB>GB，可以得到纳什均衡为(LA，GB)，企业A和企业B在t0时刻共同投资。

图3　企业A和企业B的最优投资决策

根据如上的博弈分析结果，由图3可以看到在不同值区间下企业A和企业B投资决策的纳什均衡和最优决策。

4结论

本文把实物期权方法和博弈论应用在多种风险下的研发项目投资环境中，并将阶段性的投资机会和竞争性行为结合，更加准确的对研发项目价值和收益进行评估，之后通过博弈得到纳什均衡，为企业获得最佳的时机进行投资，以实现自身收益的最大化。很多的研发项目投资是根据其他企业研发带来的正外部性以实现新产品开发，因此先行者研发的信息披露对跟随者的期权价值和收益会产生积极的影响。如果不考虑研发项目投资中的市场风险、技术风险和突发风险等不确定性因素，企业往往会高估项目的价值，这会对未来的投资决策产生不利的影响，也会对项目转让和收购的估值过分乐观。本文量化了多重风险的指标和信息披露过程的正外部性对跟随者的影响，再通过计算四种投资决策收益：先行者收益，跟随者收益，抢先同时进行投资收益，和等待市场时机再同时投资收益之后，经过博弈分析得到的纳什均衡点就是企业在多种风险下的最优投资决策。

参考文献：

[1]Margrabe W. The value of an option to exchange one asset for another[J]. Journal of Finance, 1978, 33(1): 177-186.

[2]McDonald R L, Siegel D R. Investiment and the valuation of firms when there is an option to shut down[J]. International Economic Review, 1985, 28(2): 331-349.

[3]Armada M R , Kryzanowsky L, Pereira P J. A modified finite-lived American exchange option methodology applied to real options valuation[J]. Global Finance Journal, 2007, 17(3): 419-438.

[4]Paxson D A. Sequential American exchange property options[J]. The Journal of Real Estate Finance and Economics, 2007, 34(1): 135-157.

[5]Carr P. The valuation of sequential exchange opportunities[J]. The Journal of Finance, 1988, 43(5): 1235-1256.

[6]Pennings E, Sereno L. Evaluating pharmaceutical R&D under technical and economic uncertainty[J]. European Journal of Operational Research,2011,212(2):374-385.

[7]Ghosh S, Troutt M D. Complex compound option models-Can practitioners truly operationalize them?[J].European Journal of Operational Research,2012,222(3):542-552.

[8]Thijssen J J J, Huisman K J M, Kort P M. Symmetric equilibrium strategies in game theoretic real option models[J].Journal of Mathematical Economics, 2012, 48(4): 219-225.

[9]Martzoukos S H, Zacharias E. Real option games with R&D and learning spillovers [J]. Omega, 2013, 41(2): 236-249.

[10]Koussis N, Martzoukos S H, Trigeorgis L. Multi-stage product development with exploration, value-enhancing, preemptive and innovation options[J]. Journal of Banking & Finance, 2013, 37(1): 174-190.

[11]冯晨娇,刘维奇.基于复合期权的R&D项目投资评价[J].研究与发展管理,2008,20(2):91-96.

[12]田季员,安实,张少军.基于投资跳扩散的研发项目投资决策研究[J].中国管理科学,2008,10:283-286.

[13]夏轶群, 陈俊芳.技术不确定的研发项目投资时机期权博弈分析[J].科研管理,2009,30(2):126-130.

[14]陈 涛,丛国栋,于本海,张金隆.基于风险管理的软件开发过程模型及其复合实物期权分析[J].管理工程学报,2010,24(2):61-67.

[15]杨金强,杨招军.部分信息下实物期权的定价和风险对冲[J].中国管理科学,2011,19(4):9-16.

[16]谷晓燕,何锋,蔡晨.风险条件下基于实物期权的研发项目多阶段评价模型[J].中国管理科学,2011,19(4):68-75.

[17]张新华,叶泽,李薇.价格与技术不确定条件下的发电商碳捕获投资模型及分析[J].管理工程学报, 2012, 26(3): 109-113.

[18]何沐文,刘金兰,高奇特.不确定环境下自然资源开发项目投资评价模型[J].管理科学学报,2013,16(6):46-55.

[19]吴崇,胡汉辉.不确定性和动态能力互动下企业投资竞争决策[J].管理科学学报,2013,16(5):39-54.

[20]Geske R. The valuation of compound options[J]. Journal of Financial Economics, 1979, 7(1): 63-81.

[21]Merton R C. Option pricing when underlying stock returns are discontinuous[J]. Journal of Financial Economics,1976,3:124-144.

[22]Dixit A K, Pindyck R S. Investment under uncertainty[M]. New Jersey: Princeton university press, 1994: 172-173.

[23]Dias M A G. Real options theory for real asset portfolios: the oil exploration case[C].10th Annual International Conference on Real Options. New York, USA: 2006.