教师对学生成绩预估偏差归因

教师对学生成绩预估偏差归因

王昀

摘要：高中数学教学中，教师讲过几遍的题学生在考试中仍不得分是一个普遍现象。教师教学中对学生心理需求关注不够、对学生学习动机的估计过高及解题思路不自然是造成这一现象的主要原因。分析原因，找出应对的办法对提高课堂教学效率十分有益。

关键词：思维；学习动机；数学思想方法

收稿日期：2014-11-21

作者简介：王昀， 天津市教育招生考试院(天津 300387)副研究员。

考试是反馈教与学情况的一种重要手段，是测试学生学习目标达成和评价教师教学成果的一种主要方式。从教师教的角度看，考试中得到的信息是教师教学反思最直接的依据。考试之前，教师心里会对学生成绩有一个预估值，这实际上也是对自己教学效果的一种判断，这种判断往往和学生实际得分出入很大。教师判断失误会出现这样一种普遍现象：反复练习的题目、讲过几遍的题目，学生完全应当掌握，但考试中仍不能得分。我们把这一现象称为教师对学生成绩预估偏差。除考试时学生紧张，导致思路混乱、审题不细或计算错误对成绩有一定影响外，这种现象更多地折射出教师教学中还存在着一些长期被忽视的盲区。

一、原因分析

(一)教师对学生解题的心理需求关注不够

需要是人的活动的基本源泉和动力，人的活动往往被某种需要驱使，推动有机体以一定的方式向着一定的方向进行活动，以求得自身的满足。人体所体验的需要越强烈，由它引起的活动就越有力。[1](P37)在教学设计中，教师的重心一般放在题目的选择和对解法的研究上，考虑最多的是题目难易度是否适合学生的认知水平，是否揭示数学问题之间的规律。课堂上教师关注最多的是学生是否掌握了解法，是否能运用刚学过的方法解决问题。课下教师投入最多的是布置大量不同难度的作业让学生练习，以期达到学生熟练掌握解法的目的。这是当下我国高中数学例题教学的基本模式，也是引领教师教学的基本思想。这种模式的最大优势是效果立竿见影，缺点是教学效益难以最大化，因为它缺少了一个重要环节，就是教师只是孤立地研究知识，没能充分考虑学生对知识的心理需求，一旦学生对知识的需求不强或根本没有需求，学生的学习就缺乏兴趣和动力，课上表现出来的认真、投入是一种被动状态下的行为，是教师提出问题后一种顺从的、强制的思考。

这是一位教师在一节导数复习课上讲的一道例题：

例1已知函数f(x)=ex-ln(x+m).当m2时，证明f(x)>0。

教师把解答过程分为如下四个步骤：

(1)由m≤2，得ln(x+m)≤ln(x+2)，转化为证明m=2时f(x)>0，只需证明f(x)的最小值大于零即可；

(2)判断出方程f′(x)=0有唯一实根x0，且x0∈(-1，0)；

(3)判断f(x0)是f(x)的最小值；

(4)通过代换变形，得f(x0)>0，从而f(x)≥f(x0)>0。

教师的思路分析条理清楚，丝丝入扣，学生听课的表情十分轻松。然而三周之后，一个学生拿着笔记本找到老师，说这道题当时听懂了，现在则回忆不起来当时的解法了。教师觉得这种解题方法比较重要，有必要让学生再熟悉一遍，于是上课的时候再现了这道题，出人意料的是，有近三分之一的学生对这道题毫无印象，超过一半的学生的反应是“好像讲过”，但解法不记得了，只有个别学生能说出“f′(x)=0的根求不出来，用整体代换”。

问题出在教师对例题的呈现方式上，只是简单地给出题目，缺少让学生意识到问题的特殊性进而产生情感需求的必要铺垫。

没有需要，就不会有行为目标，没有行为目标，行为就是被动的、盲目的。回顾一下我们的课堂，不难发现，一切教学活动都是在教师给出题目的前提下展开的，而教师给出题目的方式几乎都是直接的，这看似顺理成章的做法未必能让学生心理认可。学生潜意识里会有一个反问：为什么要提出这个问题？它的意义是什么？教师很少回答过这个反问，这就造成当面对题目时，学生的反应是一种习惯使然的条件反射，由于每天都要接触大量的题目，在教师眼里十分重要的题目很难对他们产生刺激，他们的大脑处于一种近乎麻木的状态。虽然接下来学生也会积极寻求题目的解决途径，甚至会有奇思妙想和不同观点的碰撞，但那不过是一种程式化的简单思维活动，留下的印象不会深刻，时间一长，遗忘在所难免。因为“对于学生的学习和发展而言，并不是所有的知识都是有效的，即使是那些科学的、正确的知识，如不能够使学生的身心素质有所增进，那也是无效的知识。”[2]无效的知识不可能在大脑中存留太长的时间。

(二)教师对学生学习动机估计过高

学习动机对学生学习的重要性已是教育工作者的共识，但在构成动机的两个要素“需要”和“诱因”上，教师很少作为，虽然也有激发动机的做法，但多停留在浅显的表层。毋容置疑，学生有着诸多的学习需要，高考升学就是高中阶段相对持久的需要，对知识的渴望、对数学的兴趣以及对教师的喜爱等都会对学习产生心理的需要。但具体到课堂上，学生对某个数学问题解法需求的强弱具有随机性，只有解法触动了学生的思维，他们才能产生真正的求知欲，而教师在教学中很少有通过自身个性化的风格，去演绎解法中蕴含的给人启迪的元素，往往对学生的学习需要和热情估计过高，认为高考要求的知识方法学生就一定会重视，因此会在教学设计时忽略学生学习的情感。同时，教师对学生“这种学习需要只是一种潜在的需要状态，还不能成为推动学习活动的动机”[1](P133)认识不足：那些不知疲倦，勤奋刻苦的学生让教师觉得升学的需要和数学题目本身就具有足够的力量使学生投身其中；至于懒于动脑的学生不过是个案。源于此，教师备课时对唤醒学习需要的“诱因”很少考虑。

下面的案例能给我们带来很多的思考。

一位教师想通过一题多解培养学生发散性思维能力，进而提高他们分析问题和解决问题的能力。

例2已知实数x，y满足x+y=1，求x2+y2的最小值。

由于题目比较简单，教师让学生说解法，很快学生就给出了两种方法。

解法1由x+y=1，得y=1-x，

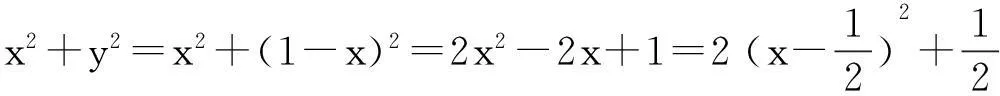
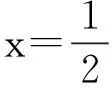
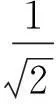
教师问还有没有其他解法，多数学生沉默思考，有的学生说了一些不成熟的想法，比如利用基本不等式求解。

见此情景，教师抓住时机展示了自己的解法。

解法4令x2+y2=k2，可设x=kcosα，y=ksinα，转化为三角问题。

在随后对课堂教学效果的访谈中，学生对本节课的两种感受给笔者留下了深刻的印象。课上那些表现出足够热情的学生的感觉是，老师的方法巧妙，开阔了自己的眼界，至于解题中会不会用，自己并不清楚，而且是当时觉得好，课下并没留下太深的记忆；课上反应平淡的学生的心理是，找到解法1、解法2后，进一步探索解法的欲望已经减退，况且老师的两种解法虽然巧妙但并不简单，没有实用价值，也就不再认真听课。

这种状态下的课堂，学生由于缺少学习动机，潜在的学习需要不能被激发出来，因此思想并没有完全活跃在课堂上。有的觉得听懂了，“听”的任务完成了，思维也就游离于课堂之外，而所谓的“懂”不过是大脑表层的感性认知，没有体验、反思、升华的过程，理解自然也就不深刻；有的看似认真听讲，但基本没有记忆，大脑没有任何加工；有的根本没听；有的似懂非懂。

在激发学生学习动机时，很多教师存在认识上的偏差，致使教师对课堂实际状况判断失真。比如，现代教学强调师生互动，教师总要创设情境调动学生，而教师设置的互动又多是围绕解题的显性方式，一旦互动形成了热闹的场面，教师便兴奋不已，觉得达到了效果。课堂中学生最高级的活动是思维的活动，场面的活跃并不一定代表思维有深度，真正触及灵魂的思考往往是无声的，然而多数教师并不喜欢“沉闷”的课堂，而是追求肢体、语言、画面带来的视觉效果，这些缺乏思维要素的活动，难以触动学生的心灵，也就留不下痕迹。

(三)解题思路不自然

学生学习解题方法的最基本途径是模仿，教师的示范是学生模仿的直接对象。教师课堂上展示的解题思路有两个来源，一是教师自己思考的结果，二是看参考书或与其他教师交流而得。教师的解题经验决定了教师的思维习惯与学生有很大的差别，但教师常常忽略这一点，习惯于用自己解题的能力去衡量学生，认为自己能想到的方法多数学生也能想到，因此在解题思路分析时对学生认知基础评估不够客观，造成解法思维跨度较大，学生感到不自然。

另一方面，一种解题方法，如果教师当时没想到，看过解答之后再深入分析，也会给解法找出合理的解释，课堂上教师就会按照自己研究后的心得展示给学生，并认为学生会接受自己对解法的解释，随着讲解次数的增多，原本自己也没想到的解法慢慢觉得顺理成章了。这种解题思路的分析，是建立在已知解题方法的基础之上，是在为已知解法寻找理由，学生记住的只是僵化的结论，并没体验到解决问题的思维过程，更没有真正理解数学思想方法应如何运用，以至于经常有学生问教师：“这种方法是怎么想到的？”可见学生虽然能够听懂，也能模仿解法解决类似的问题，但并没学会如何思考，无法引起思维上的共鸣，一旦题目情境发生变化，学生就会失去思考的依托，不知如何下手。

二、教学建议

(一)展示数学的魅力

激起学生对数学的兴趣并不是一件难事，因为兴趣的诱因在课堂中比比皆是。在这方面已有很多行之有效的方法和途径，但要使学生的兴趣保持并不断发展则需要兴趣的源泉，兴趣的源泉是学生热爱数学、探索奥秘的持久动力。教学中可以通过揭示解题方法中蕴含的丰富而深刻的数学思想来展示数学的魅力，通过数学方法的应用使学生感受到数学的价值。只有学生感受数学自身的美妙，才能喜爱数学、向往数学，才能全身心地投入到数学学习活动中去。这需要教师对数学要有自己的理解，然后通过课堂把这种理解传递给学生。

数学学习是一个感知、体验、生成的过程，教学中可根据学生的特点，设置有启发性的问题，让学生亲身经历提出问题、解决问题的整个过程，促使学生学习数学的方法，了解数学的本质，加深学生对数学思维方式的理解和认识，逐渐学会用数学的方式解决问题、认识世界，在探索问题的过程中感受数学的思维特点，在积累中丰富他们的数学情感，使数学成为学生的一种精神需要。达成这一目标的关键是教师提出的问题要有探索的价值，解决问题的方法要有吸引学生的力量。由浅入深、层层递进地提出系列问题，对典型问题逆向设问等都是可以借鉴的预设问题的方法。在上述例1的教学中，如果教师能够结合问题的实际背景或通过设置问题引起学生的注意，对初次见到这类题目的学生而言，便会产生不一样的学习态度。又如，三角代换是一种常用的解题方法，但因例2有更简单、更容易想到的方法，其价值没能得到体现，如果在较为综合的例题中使用，不仅能展现其独特的作用，而且还能激起学生的学习欲望。

(二)注重数学思想方法的运用

高中数学课程应注重提高学生的数学思维能力，这是数学教育的基本目标之一。[3](P3)数学思维能力是数学能力的一个重要组成部分，数学能力一个重要的标志是运用所学的知识、方法解决相关的问题，对学生数学能力的评价是通过学生对数学思想方法的应用来实现的。目前评价学生数学能力的主要方式是考试，而考试分数又从某种意义上反映一个学生的数学能力，因此教师对学生的考试成绩格外关注。但有一个误区，为了使学生在考试中尤其是高考中取得好成绩，教学中，对某一类数学题，教师总是试图穷尽各种题型及解法，以便让学生解答该类题目时几乎不用过多的思考，直接套用解题方法即可。这种做法可以在一定程度上提高成绩，但不能真正提高学生的数学能力，学生无法通过数学学习提高素质，发展智力。

教学中在总结规律、归纳方法的同时，要让学生在解决问题的过程中学会驾驭数学思想方法，改变问题的情境是实现这一设想的有效途径。情景改变之后的题目对学生来说是陌生的问题，学生无法直接套用已有的解题模型，需要通过观察、分析、联想，发现陌生问题中所学过的解题方法，把陌生问题转化为已知问题。改变情境之后的题目对学生的迁移能力要求较高，可以最大程度地调动学生的思维，让学生在变化中领悟数学解题的规律，摆脱僵化的思维模式，学会独立运用数学知识创造性地解决问题。

(三)示范思维过程

解题思路要自然，这是每位数学教师都追求的一种解题教学的境界，但如何做到思路自然，尤其是如何做到学生认可的思路自然，不同的理解会有不同的做法。波利亚认为，“教师应当把自己放在学生的位置上，他应当看到学生的情况，应当努力去理解学生心里想什么，然后提出一个问题或是指出一个步骤，而这是学生自己原本应想到的。”[4](P1)很明显，他主张教学要顺乎自然，这里的自然更加具体、微观，是指“问题”要贴近学生的实际，是“学生原本应想到的”。因此解题教学中，教师不要急于展示自己的解法，应给学生充分思考的时间，多听听学生的想法，尽量顺着学生的思路深入下去。学生陈述想法的过程实际上是暴露学生思维的过程，了解了学生思维的特点，教师便可有针对性地选择切入的角度。教师要避免漠视学生不成功的思路，对不成功的思路分析有助于提高学生的反思意识，促进学生思维的正向迁移。这样的教学活动是在学生“想得到”的前提下展开的，学生是带着问题学、带着目的想，其效果是不言而喻的。

在不做准备的情况下，现场讲解对教师来说是陌生的题目也是一种有益的方法，这类“陌生的题目”素材很多，如学生提出的疑难问题就可以用来现场讲解。现场讲解的目的是“让学生看到老师最自然的解题思路，让学生模仿、体验老师探索问题的轨迹，学会如何思考。”因为教师反复推敲后的讲解“只是解题方法的示范”，而现场讲解则是“思考过程的示范”[5](P295)，是教师思维过程的真实展示。这种方式可能使教师因思路受阻陷于尴尬境地，但这也正是自然思维过程的体现，对学生的积极影响是单纯介绍几种解题方法所无法替代的。

参考文献：

[1] 徐胜三.中学教育心理学[M].北京:人民教育出版社,2001.

[2] 王新民，王富英．高效数学教学构成要素的分析[J]．数学教育学报，2012(3)．

[3] 中华人民共和国教育部.普通高中数学课程标准(实验稿)[M].北京：人民教育出版社，2003.

[4] 波利亚.怎样解题[M].上海:上海科技教育出版社,2010.

[5] 梁栋.自然数学[M].天津:天津教育出版社,2012.

[责任编辑：况琳]

Reasons Why Teachers Make False

Predictions of Students’ Mathematical Achievements

WANG Yun

Abstract:It is not uncommon in senior high schools that students fail to work out the math test questions their teachers have explained many times before in the classroom teaching. The causes to this phenomenon are manifold: teachers do not pay enough attention to students’ psychological demands in classroom teaching; teachers overestimate the students’ motivation, or their methods of solving problems are ineffective. Analyzing the causes and finding out the relevant solutions will be of great help to math teachers to improve the efficiency of classroom teaching.

Key Words:thinking; learning motivation; mathematical thoughts and methods