基于LCD-Hilbert谱奇异值和QRVPMCD的滚动轴承故障诊断方法

第一作者杨宇女，博士，教授，1971年4月生

基于LCD-Hilbert谱奇异值和QRVPMCD的滚动轴承故障诊断方法

杨宇，何知义，潘海洋，程军圣

(湖南大学汽车车身先进设计制造国家重点实验室，长沙410082)

摘要：针对多变量预测模型的模式识别(Variable Predictive Model Based Class Discriminate，VPMCD)方法在参数估计中存在的缺陷，采用分位数回归(Quantile Regression，QR)代替原方法中的最小二乘法进行参数估计，克服最小二乘回归中强假设、易受异常值影响等问题，以此提高模式识别的精度。因此，提出了基于分位数回归的多变量预测模型模式识别方法(Quantile Regression-Variable Predictive Mode Based Cass Discriminate ，QRVPMCD)。采用局部特征尺度分解(Local Characteristic-Scale Decomposition，LCD)方法对滚动轴承振动信号进行分解得到若干个单分量信号，提取单分量信号的Hilbert谱奇异值组成故障特征向量，并以此作为QRVPMCD的输入进行滚动轴承故障诊断。对不同工作状态和故障类型下的滚动轴承振动信号进行了分析，结果表明了该方法的有效性。

关键词：QRVPMCD；LCD；Hilbert谱奇异值；滚动轴承；故障诊断

基金项目：国家自然科学基金(51175158, 51375152);湖南省自然科学基金(11JJ2026) 国家自然科学基金51108059；国家自然科学基金委创新研究群体基金(51121005);973项目(2015CB057704)

收稿日期：2014-01-22修改稿收到日期：2014-04-16

中图分类号:TH113

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.020

Abstract:Targeting the defects in the parameter estimation of VPMCD (variable predictive model-based class discriminate), Quantile Regression (QR) was used for parameter estimation instead of least-square approach in the original method. The questions such as strong assumptions and easiness of being affected by the outliers in the ordinary least-square regression could be overcome by QR so as to improve the accuracy of pattern recognition. Therefore, the quantile regression-variable predictive mode based on class discriminate (QRVPMCD) was proposed. The local characteristic-scale decomposition (LCD) was used to decompose the rolling bearing vibration signal into several mono-component signals, and then the Hilbert spectrum singular values were extracted from the mono-component signals to form a fault feature vector, which was then used as input of QRVPMCD for rolling bearing fault diagnosis. The analysis results under different working conditions and different kinds of failures of roller bearings demonstrate the effectiveness of the proposed method.

Rolling bearing fault diagnosis method based on Hilbert spectrum singular values and QRVPMCD

YNAGYu,HEZhi-yi,PANHai-yang,CHENGJun-sheng(State key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University, Changsha 410082,China)

Key words:QRVPMCD; LCD; Hilbert spectrum singular value; roller bearing; fault diagnosis

滚动轴承的故障诊断实质是一个对轴承工作状态和故障类型模式识别的过程，针对滚动轴承的故障诊断问题，已经有多种不同的模式识别方法，应用较广泛的有神经网络和支持向量机(Support Vector Machine，SVM)等模式识别方法，但是它们都存在一些无法克服的缺陷[1-2]。更为重要的是神经网络和SVM都忽略了作为输入的特征值之间的内在关系，然而在滚动轴承故障诊断中所提取的特征值之间都有一定的内在联系。近年来，Raghuraj等提出了基于多变量预测模型的模式识别(Variable Predictive Mode Based Class Discriminate ，VPMCD)方法，该方法考虑了所提取特征值之间的内在联系，同时还与神经网络、支持向量机等其它模式识别方法进行了对比，结果验证了VPMCD方法的有效性和优越性[3-4]。

VPMCD方法是用最小二乘回归(Ordinary Least-Square Regression，OLSR)对模型的参数进行估计，然而最小二乘回归是建立在自变量X=x下因变量Y的条件均值与X的关系的线性模型，尤为重要的是最小二乘回归是在强假设条件下进行的参数估计，最小二乘回归的随机误差项εi之间必须互不相关且要服从正态分布同时各自方差相同，这样必将导致最小二乘回归容易受到自变量中一些异常值和极端值的影响。在实际滚动轴承的故障诊断中，所采集得到的数据往往出现有一定的异常值和极端值，导致由最小二乘回归得到的回归系数与理想的回归系数存在较大偏差，进而影响VPMCD的分类效果。

分位数回归(Quantile Regression，QR)[5]是对普通最小二乘回归的一种改进，其根据因变量Y的条件分位数对自变量X进行回归，得到所有分位数下的回归模型，这样更能精确地描述自变量X对因变量Y的变化范围及条件分布形状的影响，从而进行全面地分析，当数据出现偏态分布或者是严重偏态分布时也能得到满意的结果，得到的回归系数估计也比最小二乘回归系数估计更稳健。因此，本文采用分位数回归代替最小二乘回归，提出了基于分位数回归的多变量预测模型模式识别方法(Quantile Regression-Variable Predictive Mode Based Class Discriminate ，QRVPMCD)。

滚动轴承故障诊断在进行模式识别前必须提取有效的特征值，当滚动轴承出现故障时，其振动信号往往表现出非平稳、非线性等特征。时频分析方法中局部特征尺度分解(Local Characteristic Scale Decomposition，LCD)算法[6]是一种新的基于极值点的局部特征尺度参数的自适应、非平稳信号处理方法，它能自适应地将信号分解为一系列瞬时频率具有物理意义的内禀尺度分量(Intrinsic Scale Component，ISC)。同时LCD算法能克服经验模态分解(Empirical Mode Decomposition，EMD)[7]中诸如过包络、欠包络、端点效应[8]等问题，而相比于由Mark G.Frei提出的固有时间尺度分解方法(Intrinsic Time-Scale Decomposition，ITD)[9]，LCD算法对算法本身和分解得到的ISC分量的物理意义都进行了阐述。基于此，论文用LCD分解算法对原始振动信号进行分解。另外，Hilbert谱表示信号完整的时间—频率分布，能够准确地描述信号的幅值在整个频率段上时间和频率的变化规律，在故障分析中Hilbert谱包含了机械故障中非常丰富的信息；同时矩阵的奇异值是矩阵的固有特征，具有较好的稳定性。因此论文选用Hilbert谱和奇异值分解对LCD处理后的信号进行特征提取。

综上所述，本文将Hilbert谱奇异值和QRVPMCD应用于滚动轴承的故障诊断中。首先采用局部特征尺度分解(Local Characteristic-scale Decomposition，LCD)方法将滚动轴承的振动信号分解为若干个内禀尺度分量(Intrinsic Scale Component，ISC)；接着求取每个振动信号前几个ISC分量的Hilbert谱，并将Hilbert谱的奇异值作为特征值来构成特征向量；最后利用QRVPMCD对所得的特征向量进行模式识别。通过实验数据的分析，验证了该方法的有效性，从而为滚动轴承的故障诊断提供一个新的方法。

1QRVPMCD方法原理

1.1分位数回归

分位数回归方法归类于非参数检验，其基本思想和最小二乘回归相同，都是设法使得所构建的方程和样本之间的距离最短[10]。但是分位数回归对总体不要求正态分布，减弱了随机误差项的正态性要求，并且分位数回归考虑整个分布信息以及各分位点的影响。分位数回归系数估计通过使下式完成最小值线性规划得以完成：

(1)

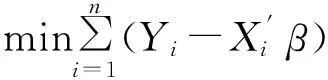
1.2分位数回归(QR)和最小二乘回归(OLSR)仿真对比

在线性回归分析中经常用最小二乘法进行数据的拟合运算，即是最小二乘回归(OLSR)。Raghuraj与Lakshminarayanan提出的VPMCD方法在预测模型的训练过程中就是采用OLSR进行参数估计，一般情况下用OLSR能得到很好的结果，但是OLSR是在基于强假设的条件下进行的参数估计。在用OLSR进行回归估计时，它要求其随机误差项服从正态分布、方差相同且各不相关、同时要求与自变量之间互不相关，在这些强假设下一旦自变量数据出现极个别的异常值或者极端值都将很大程度上影响OLSR估计的参数，从而导致估计值与真实值出现较大的偏差。

分位数回归(QR)作为最小二乘回归(OLSR)的有效补充，它不要求在强假设条件下进行回归分析，同时能不断地调整分位数值得到一系列的回归曲线，然后选取最合适的一条回归曲线的系数作为参数估计值。

为对比QR与OLSR在自变量数据出现异常值情况下的预测结果，本文选取在一个自变量x情况下的20组数据进行对比分析，假设两者满足关系式y=β0+β1x。当20组数据中没有异常值情况下两种方法拟合曲线如图1所示。

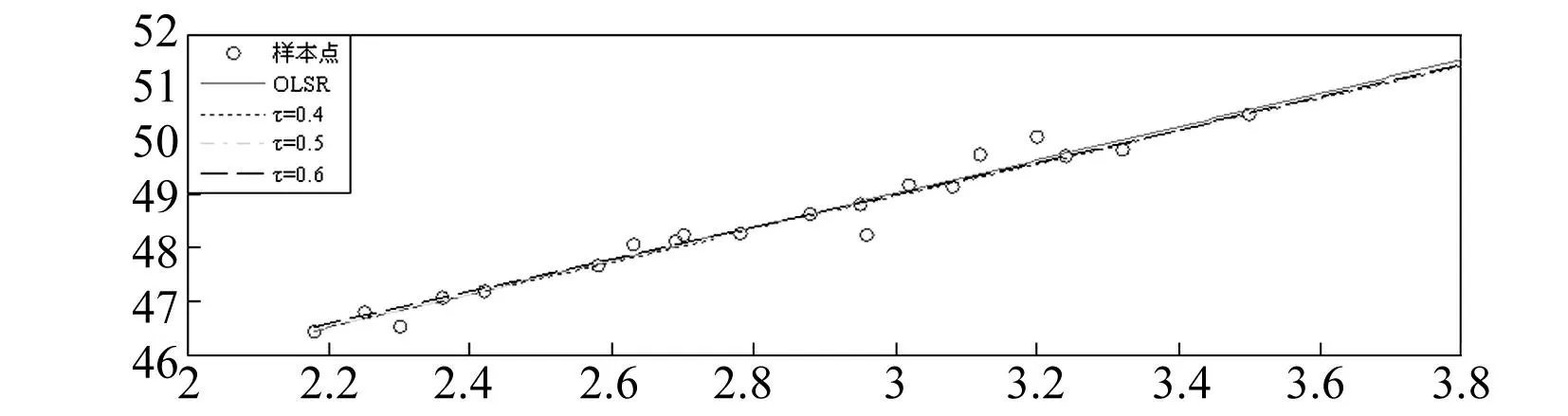
图1　样本数据无异常值时两种方法拟合曲线 Fig.1 The fitting curves of two methods when sample data is constant

从图1中可以看出两种方法拟合出来的曲线基本重合，为方便图示表示，图中只绘出了在分位数值τ取0.4、0.5和0.6三种情况下拟合得到的曲线，实际上在这种样本数据情况下τ取0到1之间的任意值得到的拟合曲线基本重合。

当这20组样本数据出现一个异常值或极端值时两种方法拟合得到的曲线如图2所示。

图2　样本数据出现异常值时两种方法拟合曲线 Fig.2 The fitting curves of two methods when sample data has abnormal value

两种情况下通过两种方法分别拟合得到的系数如表1所示。

表1　两种情况下拟合得到的系数

图2中可以看出当同样的样本数据中出现一个异常值时，通过OLSR拟合出来的曲线发生明显的变化，而通过QR在分位数值τ取0.4、0.5和0.6三种情况下拟合得到的曲线基本保持不变；通过表1对比拟合得到的系数，在有无异常值两种情况下，OLSR两次拟合系数发生较大偏差，而QR拟合得到的系数表现出足够的稳健性。因此，在样本数据中出现极个别异常值时，QR拟合不易受异常值的影响，能得到比OLSR更稳健的拟合系数。

在上述讨论中也只绘出了分位数值τ取0.4、0.5和0.6三种情况下的拟合曲线，而实际上在QR中τ的取值是0到1中的任意值，当样本数据中出现严重偏态分布时，τ的取值相应地发生变化，以此来得到满意的拟合曲线。

1.3QRVPMCD模型

作为一种基于变量预测模型的模式识别方法，VPMCD充分利用作为输入的特征值之间的内在关系来建立数学模型，通过输入的各类样本数据估计出模型参数，以此得到不同类别的预测模型，然后利用所得到的预测模型对所需要的测试样本进行预测分类。

在QRVPMCD中，对于一类故障我们选取p个不同特征值X=[X1,X2,…,Xp]，利用分位数回归估计得到的参数建立相应的数学模型(四种模型：线性模型(L)、线性交互模型(LI)、二次交互模型(QI)、二次模型(Q))，然后采用特征值Xj对Xi进行预测(其中i≠j)，得到Xi的预测模型VPMi：

Xi=f(Xj,b0,bj,bjj,bjk)+e

(2)

式中Xi称作为被预测变量，Xj(i≠j)称作为预测变量，e为预测误差，b0、bj、bjj和bjk为参数模型，由分位数回归估计得到。

QRVPMCD模型的训练过程：

①对于g类故障分类问题，收集n个训练样本，每一类样本数分别为n1,n2,…,ng，并对所有的训练样本提取特征值X=[X1,X2,…,Xp]。

②对任的预测变量Xi，选择相应的模型类别、预测变量以及模型阶数。其中特征值的不同也会致使所选择的模型类别、预测变量以及模型阶数各不相同。

③令k=1，对nk个第k类训练样本中的任意一个样本，对每一个特征值Xi建立数学模型，则每一个特征值可以建立nk个方程，然后利用分位数回归对这nk个方程的模型参数b0、bj、bjj和bjk进行参数估计，得到(2)中Xi的预测模型VPMi。

④令k=k+1，重复步骤③，直至k=g循环结束。

改进VPMCD模型的分类过程：

①选择测试样本，并提取相应的特征值X=[X1,X2,…,Xp]。

2基于Hilbert谱奇异值和QRVPMCD的滚动轴承故障诊断方法

本文基于LCD分解技术求出轴承故障振动信号的Hilbert谱的奇异值作为特征值，然后结合QRVPMCD模式识别方法来识别滚动轴承的故障，其故障识别的框图如图3所示。

图3　滚动轴承故障识别框图 Fig.3 Diagram of the rolling bearing fault diagnosis

基于Hilbert谱奇异值和QRVPMCD的滚动轴承故障诊断方法步骤如下：

①在一定的转速下以采样频率fs对滚动轴承正常、外圈故障、内圈故障、滚动体故障四种状态进行采样，每种状态各自采集N个样本；

②利用LCD对采集得到的样本信号进行分解，得到若干个ISC分量；

③求出每种状态下各个样本前i个ISC分量的Hilbert谱，然后求出各个Hilbert谱的奇异值组成特征向量，这样每种状态下就可以得到一个N×i特征向量矩阵；

⑤将每种状态剩余的特征向量作为测试数据，用已经训练好的预测模型对其进行状态分类和识别。

3实验应用分析

为了验证论文QRVPMCD方法对滚动轴承故障诊断的实际可行性，采用湖南大学现场实际数据[11]，选用的滚动轴承为6307E型深沟球轴承，故障是通过激光切割在滚动轴承的内圈和外圈上开槽来模拟，槽宽为0.15 mm，槽深为0.13 mm，转速为680 r/min，采样率为4 096 Hz。由于实验条件的限制，未能在滚动体上设置故障，实验中调速电机为直流伺服电机，功率为600 W。实验采集滚动轴承正常、外圈故障和内圈故障三种状态下的振动信号各100组作为样本数据。内圈故障下的滚动轴承振动信号如图4所示，其经过LCD分解后得到的分量如图5所示，从图5中可以看出分解结果的前四个分量包含了原始信号的主要信息。

图4　内圈故障状态下滚动轴承振动信号时域波形 Fig.4 Rolling bearing vibration signal waveform in time domain of the inner ring fault condition

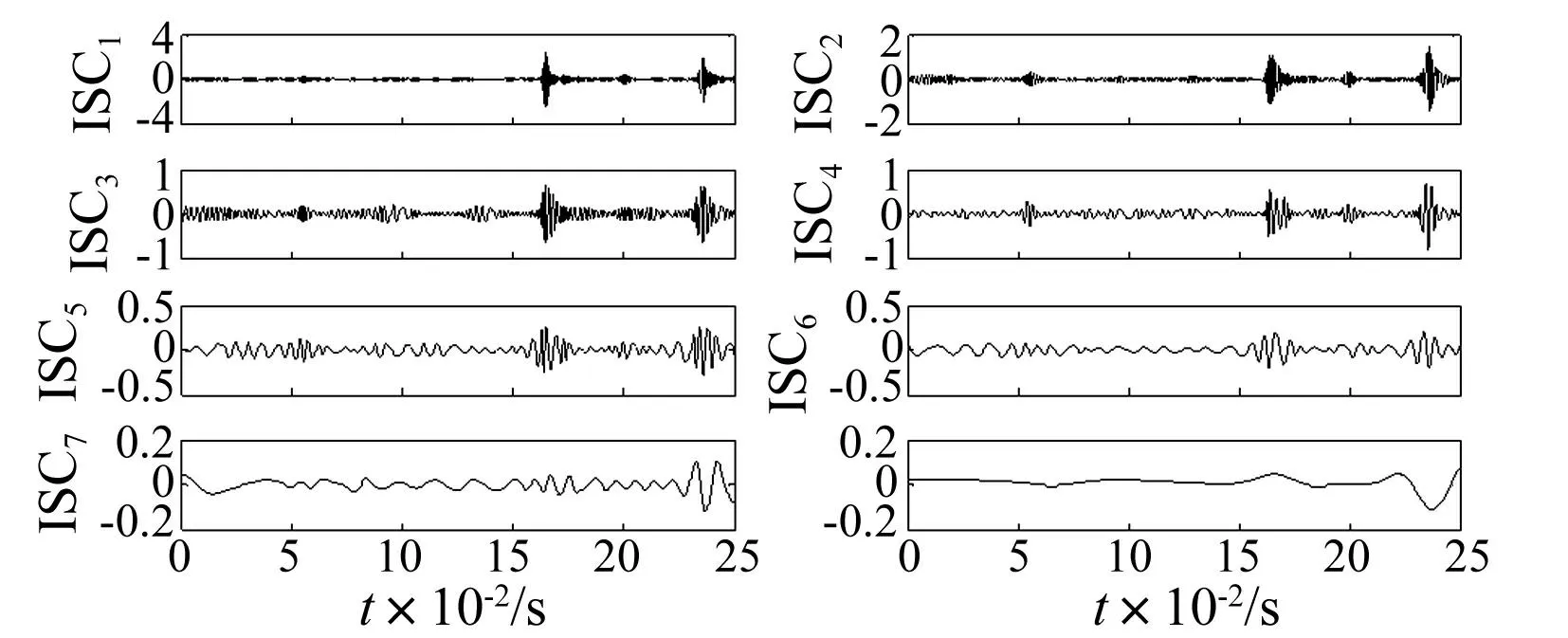
图5　内圈故障状态下的振动信号LCD分解后的分量 Fig.5 The components of vibration signal in time domain of the inner ring fault condition after LCD decomposition

首先对所采集的每个信号进行LCD分解得到若干个ISC分量，对包含主要状态信息的前四个ISC分量求Hilbert谱，然后提取各Hilbert谱的奇异值作为特征值，分别记为X1,X2,X3,X4；依次对所有样本作类似变换构成特征向量矩阵。然后随机选取100个样本中的60个样本的特征向量作为训练样本，其余的40个作为测试样本。另外，在进行故障诊断之前，采用交叉检验方法选取QRVPMCD中的τ值，论文中选取分位数值τ从0到1，间隔为0.05，将60个训练样本在K-fold cross-validation(简称K-CV)检验下得到不同识别率如图6所示(其中K=10)。

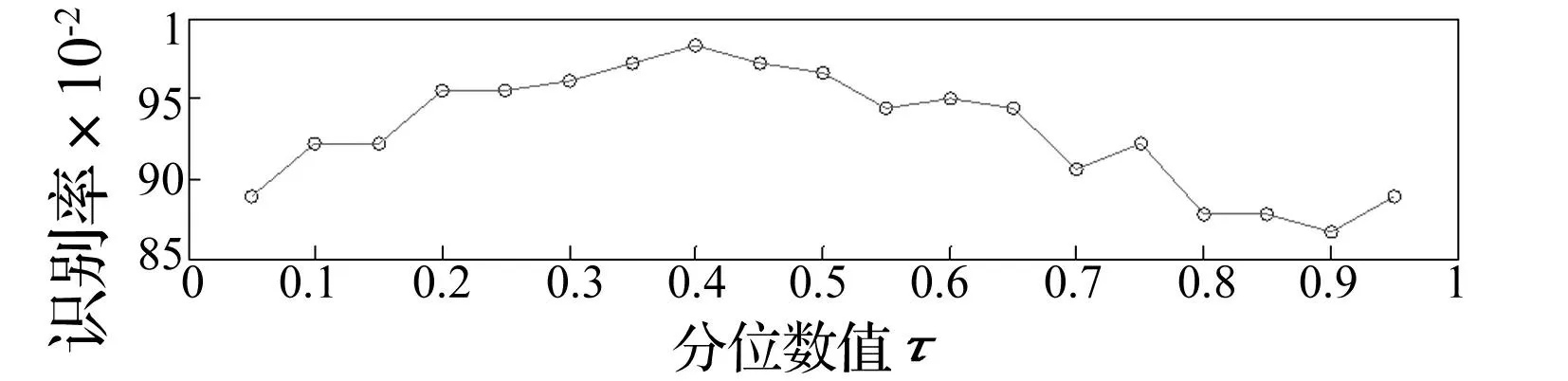
图6　不同分位数值下的识别率 Fig.6 Recognition rates in the different quantiles

从图6中得出，训练样本在10-CV检验下的识别率首先随着分位数值τ的增大而上升，在τ=0.4处有最高识别率，然后又随着τ的增大而逐渐降低，因此在本文中选取分位数值τ=0.4。将60个训练样本和40个测试样本输入原VPMCD分类器和QRVPMCD分类器中进行训练和测试。分别得到的识别结果如表2所示。

表2　两种方法下滚动轴承故障诊断的识别率

由上表可以看出两种分类方法都有较高的识别率，但QRVPMCD比原有VPMCD还是有3.33个百分点的提高。QRVPMCD在外圈故障和内圈故障下的识别率都有所提高，说明QRVPMCD和原VPMCD的预测模型发生了变化，对比两种方法的模型及阶次如表3和表4所示。

表3　VPMCD训练得到的最佳模型类型和最佳模型阶数

表4　QRVPMCD训练得到的最佳模型类型和最佳模型阶数

两种方法中的最佳模型类型和最佳模型阶数都是基于最小误差平方和得到的，对正常状态下在VPMCD和QRVPMCD中最佳模型类型的选择作定量分析如表5、表6所示。

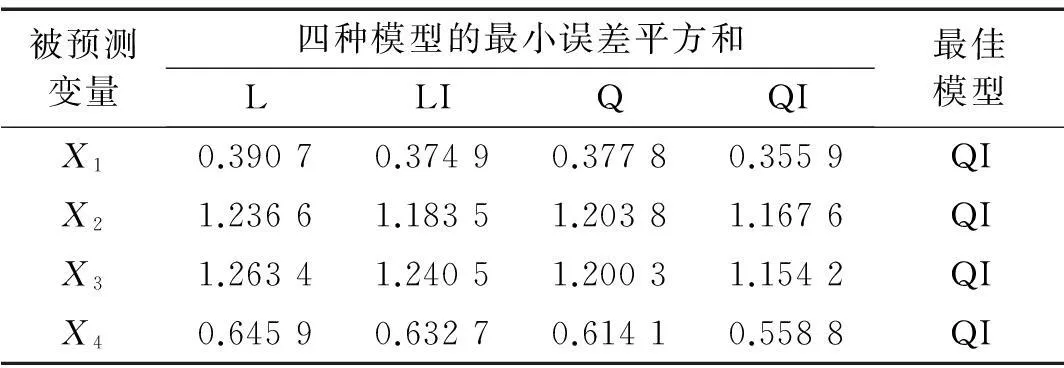
表5　正常状态下VPMCD训练得到的最佳模型选择结果

表6　正常状态下QRVPMCD训练得到最佳模型选择结果

从表5和表6中可以看出，两种方法都是选取误差平方和最小的模型作为最佳模型，其它状态的最佳模型和最佳模型阶数的选择都是类似的过程，基于篇幅原因文中只列出这一种情况。

原VPMCD方法中通过训练得到的都是三阶二次交互模型，而QRVPMCD方法中随着被预测变量和状态的不同训练得到的模型类型和模型阶数都各不相同。在原VPMCD中用最小二乘回归进行参数估计选择的模型类型和阶数都一样致使一些具有异常值或极端值的样本未能识别，而在QRVPMCD中用分位数回归代替最小二乘回归，当样本中出现有偏态分布或误差较大时能适时地改变训练的预测模型和阶数，从而得到更好的识别结果。

为更好的验证QRVPMCD比原VPMCD能有更好的识别效果，论文分别用K-fold cross-validation(简称K-CV)检验、Jack-knife(简称JK)检验、Re-substitution(简称RS)检验对上述样本的两种方法进行验证。K-fold cross-validation和Jack-knife检验是较为客观和严格的交叉检验[12]，能反映算法的推广能力；而Re-substitution检验能验证算法的自相容性[13]。三种检验方法(其中K-CV检验的K=10)得到的识别率如表7所示。

表7　三种检验方法得到识别率

从表7中可以看出，在三种检验方法下两种分类都有很高的识别率，但是QRVPMCD在三种检验下的识别率均要高于原VPMCD。其中RS检验的识别率对比说明用分位数回归代替最小二乘回归的QRVPMCD方法在算法的自相容性方面更优于原VPMCD，10-CV检验和JK检验的结果说明QRVPMCD方法在算法的推广能力方面也要好于原VPMCD。

通过上述实验数据的对比分析，在模式识别的过程中，VPMCD方法通过最小二乘回归进行参数估计得到相应的模型及阶数；而QRVPMCD方法通过分位数回归不断循环改变分位数值，来选择最佳模型及阶数，同时也获得了更高的识别率结果。在三种检验下对比两种分类方法的识别结果，QRVPMCD都取得了更好的实验效果。因此说明QRVPMVD方法能够有效地应用于滚动轴承的故障诊断中。

4结论

针对VPMCD中最小二乘回归在参数估计时的缺陷，本文提出QRVPMCD方法，用分位数回归代替最小二乘回归进行参数估计，并将QRVPMCD方法应用于滚动轴承故障诊断中，通过实验分析得到以下结论：

(1)在振动信号的特征提取过程中，用振动信号分解所得到单分量信号的Hilbert谱奇异值作为特征值，所提取得到的Hilbert谱包含时间和频率两个方面的信息，能很好地包含振动信号的故障特征信息，结合奇异值分解实现轴承的特征提取。

(2)QRVPMCD方法用分位数回归代替原VPMCD中的最小二乘回归进行参数估计，克服了最小二乘回归在样本出现偏态分布、误差较大或样本数据中出现异常值情况下难以得到较为稳定的回归参数的不足。

(3)三种检验方法对比VPMCD和QRVPMCD的识别效果验证了QRVPMCD不仅具有非常高的识别精度，而且在自相容性、推广性方面都要优于原始VPMCD方法，同时也证明了QRVPMCD能够有效地对滚动轴承工作状态和故障类别进行模式识别。

本文对实验振动信号作LCD分解后得到若干个ISC分量，对同一振动信号的前几个ISC分量提取得到的Hilbert谱奇异值都具有一定的内在联系，但是这种具体的内在联系形式难以确定，而且这些特征值之间相互内在联系的实际预测模型也无法得到。然而，本文的重点在于利用特征值之间的相互内在联系来建立预测模型，从而达到模式识别的目的，这种内在联系的具体情况并不需要知道，相应的实际模型也可以利用具体的模型来近似代替，只要达到所需要的分类精度即可。VPMCD方法和QRVPMCD方法都是在假设特征值之间存在相互内在联系的前提下，通过训练样本从四种预测模型(L型、LI型、Q型和QI型)中选择最佳预测模型，以此作为实际模型的近似模型，并通过近似模型对测试样本进行测试，从而对滚动轴承的故障类型和工作状态进行分类。

参考文献

[1]Wang C C, Kang Y,Shen P,et al. Applications of fault diagnosis in rotating machinery by using time series analysis with neural network [J]. Expert Systems with Applications, 2010, 37(2):1696-1702.

[2]Wang Hua-qing, Chen Peng. Intelligent diagnosis method for rolling element bearing faults using possibility theory and neural network [J]. Computers & Industrial Engineering, 2011, 60(4): 511-518.

[3]Breiman L. Heuristics of instability and stabilization in model selection [J].The Annals of Statistics, 1996, 24(4): 2350-2383.

[4]杨宇，李杰，潘海洋,等.VPMCD和改进ITD的联合智能诊断方法研究[J]. 振动工程学报,2013,26(4):608-616.

YANG Yu,LI Jie,PAN Hai-yang,et al.Research on Combined intelligent diagnostic method based on VPMCD and improved ITD[J]. Chinese Journal of Mechanical Engineering, 2013,26(4):608-616.

[5]Koenker R,Bassett G W.Regression quantiles [J].Econometrica,1978,46:33-50.

[6]程军圣,郑近德,杨宇.一种新的非平稳信号分析方法—局部特征尺度分解[J].振动工程学报,2012, 25(2):215-220.

CHENG Jun-sheng, ZHENG Jin-de, YANG Yu. A nonstationary signal analysis approach—the local characteristic-scale decomposition method[J].Journal of Vibration Engineering, 2012, 25(2): 215-220.

[7]Cheng J S, Yu D J, Yang Y. Energy operator demodulating approach based on EMD and its application in mechanical fault diagnosis[J].Chinese Journal of Mechanical Engineering, 2004,40(8):115-118．

[8]Huang N E, Wu M-L C, Long S R. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis [J].Proceedings of the Royal Society of London. A, 2003, 459: 2317-2345.

[9]Frei M G, Osorio I. Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals [J]. Proceedings of the Royal Society. A, 2007, 463: 321-342.

[10]Koenker R, D’Orey V. A remark on computing regression quantiles[J].Applied Statistics, 1993,43:410-440.

[11]Yang Yu, Yu De-jie, Cheng Jun-sheng. A roller bearing fault diagnosis method based on EMD energy entropy and ANN[J]. Journal of Sound and Vibration, 2006, 294: 269-277.

[12]Mardia K V, Kent J T, Bibby J M. Multivariate analysis[M]. London: Academic Press,1979. 322, 381.

[13]Cai Y D, Ricardo P W, Jen C H,et al. Application of SVM to predict membrane protein types [J]. Journal of Theoretical Biology, 2004,226: 373-376.