基于等几何裁剪分析的拓扑与形状集成优化

第一作者傅晓锦男，博士，教授，1964年11月生

基于等几何裁剪分析的拓扑与形状集成优化

傅晓锦1，龙凯2，周利明1，阙春兰1，叶航1

(1. 上海电机学院机械学院，上海200245； 2. 华北电力大学新能源电力系统国家重点实验室，北京102206)

摘要：提出了将设计和分析、拓扑与形状优化集成的思想，探索了基于等几何裁剪分析的拓扑与形状集成优化设计算法，该方法统一了结构优化的计算机辅助设计、计算机辅助工程分析和优化设计的模型，基于B样条的等几何裁剪分析既能准确表达几何形状，又可以用裁剪面分析方便处理任意复杂拓扑优化问题，由裁剪选择标准确定合理的拓扑结构变动方向，结构变动时无需重新划分网格，设计结果突破初始设计空间的限制，还可方便优化形状。建立了等几何裁剪灵敏度分析的计算方法，给出了等几何裁剪分析拓扑与形状集成优化算法，通过典型实例表明所用方法的正确性和有效性。

关键词：形状优化； 灵敏度分析； 拓扑优化； 等几何分析； 裁剪B样条； 有限元分析

基金项目：国家自然科学基金(11202078);上海市教委科研创新重点项目(13ZZ145);上海市自然科学基金(11ZR1413800)

收稿日期：2014-02-24修改稿收到日期：2014-04-21

中图分类号:O241；TH122

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.026

Abstract:An idea of integration of computer aided design, computer aided engineering analysis, topology and shape optimization design was introduced and a kind of optimization strategy for integation of topology and shape optimization design of continuum structure based on isogeometric trimmed surface analysis was explored. The proposed method offers a unified model of computer aided design, computer aided engineering and optimization design in structure optimization. The isogeometric trimmed surface analysis based on B splines has the capability of both expressing the geometry shape accurately and solving arbitrarily complex topology optimization problem. The trimmed criteria selected determine the reasonable direction of topology changes. It does not need to remesh during structural optimization process. The design results can be beyond the limitations of initial design space. It is also convenient in shape optimization. In the integration method, the calculation approach for sensitivity analysis of isogeometric trimmed surface, and the algorithm for integation of topology and shape optimization design based on isogeometric trimmed analysis were developed. A numerical example illustrates the correctness and effectiveness of the method.

Integration of topology and shape optimization design of continuum structure based on isogeometric trimmed surface analysis

FUXiao-jin1,LONGKa2,ZHOULi-ming1,QUEChun-lan1,YEHang1(1. School of Mechanical Engineering, Shanghai Dianji University, Shanghai 200245,China 2.State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206,China)

Key words:shape optimization; sensitivity analysis; topology optimization; isogeometric analysis; trimmed B-spline; finite element analysis

计算机辅助结构优化设计是一项多学科相交叉的新技术。它的研究领域涉及到力学、机械、结构工程、数学和信息技术，具有巨大的发展潜力[1-3]。我国程耿东院士和郭旭在布局优化研究中提出求解奇异最优解的松弛算法，是具有重要意义的贡献[4]。Michael等[5]提出一种的水平集方法(Level set method)，优化问题中结构的边界用嵌入到高维尺度函数中的水平集模型来表示，模型在描述复杂结构的拓扑及边界变化方面具有较好的灵活性。目前，多数研究者先计算机辅助设计(Computer Aided Design，CAD)，之后，进行计算机辅助工程(Computer Aided Engineering，CAE)分析，几何和分析模型会有出入，CAD/CAE模型难以融合[6-7]，优化方法的最优解与初始产生空洞的数量与位置有很大关系[8-9]。其中存在二个明显的问题：第一，设计空间与初始网格有关，设计空间为固定网格，设计结果与设计空间相关，若限制设计空间，有可能得不到解。另一方面，若网格划分过细，会使计算量大大增加。第二，将计算结果返回到CAD系统的后处理工作量也大，这是由于常规优化方法设计和分析的模型不是CAD系统中样条数据，需要大量的后处理工作。第一个缺点可采用无网格解决。克服第二个缺点需要统一设计和分析的模型[10-11]。Hughes等[12]提出了一种等几何分析的新型有限元方法，该方法采用Non-Uniform Rational B-Splines (NURBS)作为有限元离散的插值函数，将控制顶点作为网格节点，使CAD和CAE之间通信既方便容易，又有效[13-17]。在Hughes等[18-25]几何分析的启发下，很多学者在结构优化领域结合等几何分析进行了广泛的研究，优化技术迅速发展，创造了不少成果，具有较好的参考价值。但以上文献的拓扑优化方法多采用细胞或单元，然而，细胞表示的拓扑是不规则或模糊边界轮廓，所以，试图研究一种能确定的光滑的材料边界的方法，最近，水平集拓扑优化已被广泛的研究[26]，水平集拓扑优化中，由雅可比方程确定进化水平集函数表示材料边界，设计灵敏度分析计算形状速度，一般，水平集拓扑优化有一个严重的不足，在优化过程中，新的内部空洞不能自动产生，所以，初始的水平集会包含一些用户定义的内部空洞，这样，该拓扑优化方法的问题是会依靠初始空洞的数量和位置，在优化过程中，合理的策略应该是基于拓扑灵敏度和应变能量密度引入新的空洞。本文在前期集成优化研究的基础上[27-28]，探索等几何裁剪灵敏度分析方法，利用裁剪面分析任意复杂拓扑结构，无需将其分成多块，从而降低由于分块引起的巨大计算量，有限元模型与几何实体重合，统一了CAD、CAE和优化设计的模型。

1几何造型

非均匀有理B样条(Non-Uniform Rational B-Splines，NURBS)为曲线曲面几何造型主要方法[29-31]。

1.1节点矢量与B样条

节点是参数轴上的分割点，一个非递减的参数坐标的集合定义为节点矢量，记为

Ξ=[ξ0,ξ1,…ξn+p]

式中，ξi∈R是第i个节点，p是B样条基函数的次数，n是基函数的数量。

定义B样条基函数

(1)

(2)

用n个p次B样条基函数Ni,p(ξ)(i=1,2,…,n)和n个控制顶点Pi(i=1,2,…,n)确定p次B样条曲线：

(3)

1.2NURBS描述

(4)

NURBS曲线可表示为

(5)

由节点矢量ξ=[ξ0,ξ1,…ξn+p]和节点矢量η=[η0,η1,…ηm+q]，n×m个控制顶点Pi,j(i=1,2,…,n;j=1,2,…,m)，构成的B样条曲面：

(6)

由节点矢量ξ=[ξ0,ξ1,…ξn+p]、节点矢量η=[η0,η1,…ηm+q]和ζ=[ζ0,ζ1,…ζm+q]，n×m×l个控制顶点Pi,j,k(i=1,2,…,n;j=1,2,…,m;k=1,2,…,l)构成的B样条体：

S(ξ,η,ζ)=

(7)

1.3基于NURBS的等几何分析

建立准确的几何模型是等几何分析的关键，CAD(计算机辅助设计)和CAE(计算机辅助工程分析)是同一个模型，即等几何，用有限元方法进行分析。用B样条基函数代替多项式基函数，控制顶点视同有限元节点，可得：

(8)

式中，u为如位移、应力和应变等控制变量的物理场，d可以为控制顶点的位移、应力和应变等。

2裁剪面分析

常规的等几何分析时，分析模型是分解成几个B样条小块，所以，若拓扑结构复杂，分析较为困难，若借助计算机图形学的裁剪操作，即使复杂模型也容易实现。裁剪单元按照单元的顶点数量分为三类，如图1所示。复杂的裁剪单元与这三类裁剪单元不匹配，那么继续四分细化该单元，直到满足这三类的其中一类为止。裁剪单元继续分为三角形和曲边三角形，曲形三角形有一边为B样条裁剪曲线。

图1　三类裁剪单元 Fig.1 Three kind of trimmed elements

因参数空间比物理空间简单，故单元分解在未裁剪的参数空间操作。单元刚度矩阵为

(9)

B=MΓG

(10)

其中，Jξ为由参数空间向物理空间转换的变换矩阵，表示为

(11)

J=JTkJTn=

(12)

如图2所示，在有限元中，线性变换Tkt能用线性三角形形状函数表示。

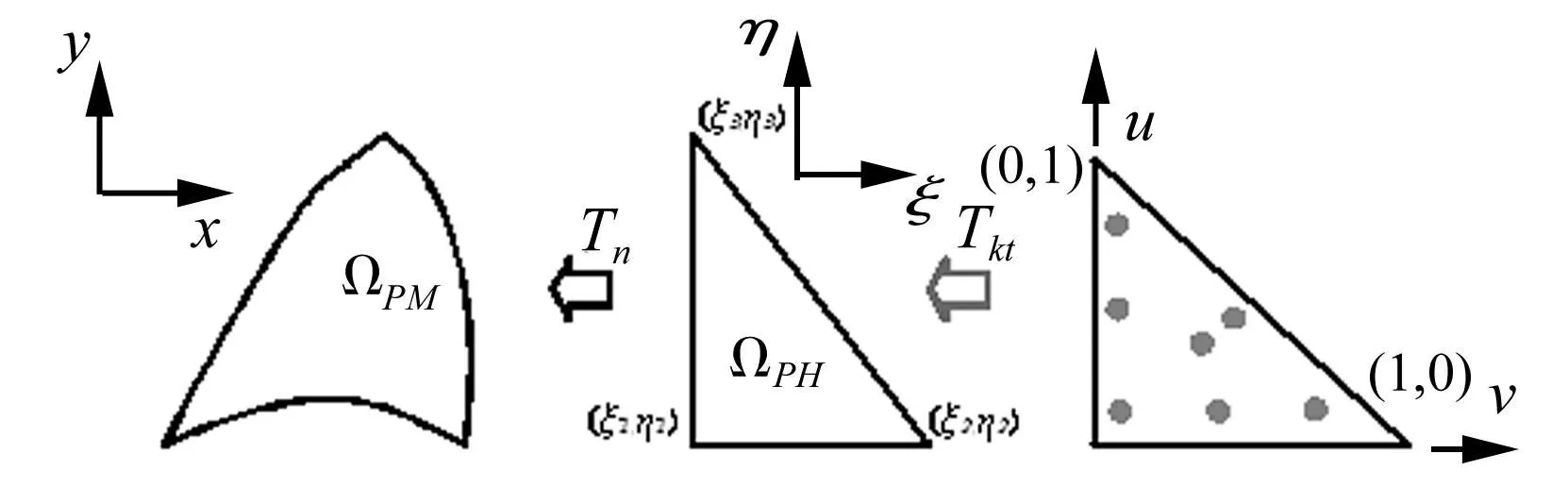
图2　三角形单元变换 Fig.2 Transformations in triangular elements

为方便积分，采用线性变换Tkt

Tkt:{u,v}→{ξ,η}

(13)

如图3所示，正积分三角形单元的二顶点(ξ1,η1)和(ξ2,η2)与裁剪矩形单元的顶点一致，另一点(ξ3,η3)位于裁剪曲线上，可求裁剪曲线交点及其参数。假定，点(ξ3,η3)中，ξ3为已知，η3为未知。

(1)由已知参数用下式可求λ0

(2)由下式求得未知参数

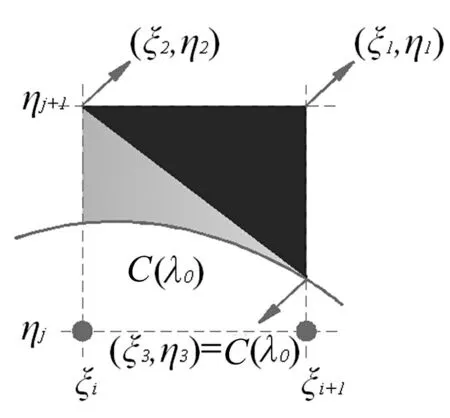
图3　在三角形单元中求裁剪曲线交点及其参数 Fig.3 Finding intersection and its corresponding parameter of trimming curve in triangular elements

正三角形单元的雅可比矩阵为

(14)

图4为由高斯积分单元转化为物理空间曲边单元，物理空间单元用ΩPH表示；相应参数空间单元用ΩPM表示。

图4　曲边三角形积分单元变换 Fig.4 Transformations in curved triangular integration elements

(1)由已知参数用下式可求λ1

(2)由下式求得未知参数

假定，点(ξ3,η3)，ξ3为已知，η3为未知。

(1)由已知参数用下式可求λ2

(2)由下式求得未知参数

图5　在曲边三角形单元中求裁剪曲线交点及其参数 Fig.5 Finding intersection and its corresponding parameter of trimming curve in triangular elements

在图4中，线性变换Ti，Tj和Tkt为

(16)

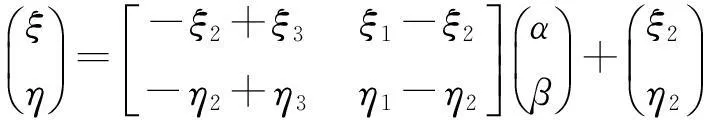
(17)

在αβ坐标系φ(λ)=[φα(λ),φβ(λ)]T裁剪曲线能用逆矩阵R-1变换

φ(λ)=R-1·C(λ)=A-1(C(λ)-Z)

(18)

曲边积分三角形单元的雅可比矩阵为

J=JTiJTjJTktJTn=

(19)

式中，

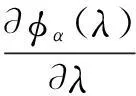
(20)

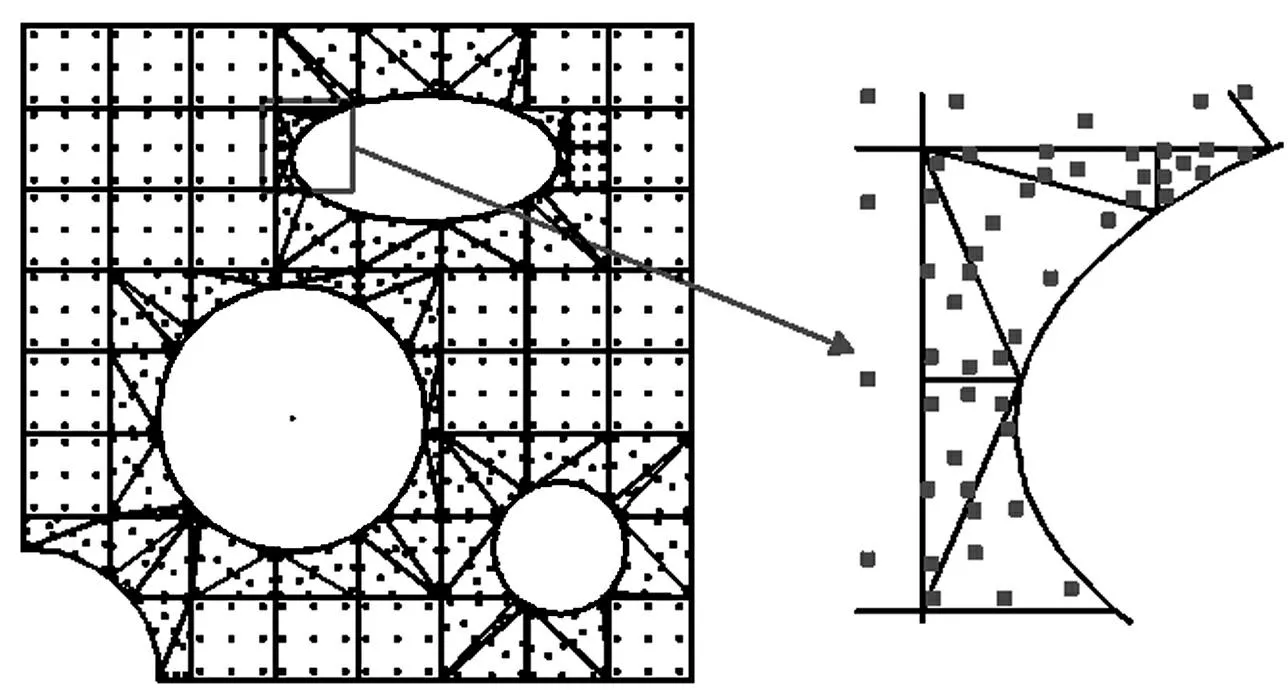
图6　积分单元分解和单元的积分点 Fig.6 Integration elements decomposition and integration points in the elements

图6显示积分单元分解和积分点。单元按图5规则分解，在曲边三角形积分单元中的积分点均布在边界，曲边三角形积分单元的刚度矩阵由式(19)和式(9)计算可得。

3裁剪灵敏度分析

本文取边界控制顶点的坐标为设计变量，建立优化模型

MinΨ(X,u(X))

s.t.hj(X,u(X))=0j=1,…,p1

(21)

3.1灵敏度计算

目标函数方程

(22)

式中，F为线性方程的力矢量，u为位移矢量。

目标函数对设计变量的灵敏度为

(23)

对式(9)的单元刚度矩阵求导

(24)

对B的导数

(25)

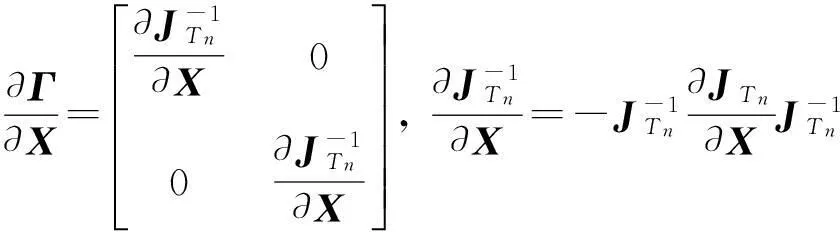
对于矩形单元：

对于正三角形单元：

对于曲边三角形单元：

(26)

用式(25)和式(26)代入式(24)求得单元刚度敏度，由此可得总刚度敏度

(27)

式中，ne为单元数量。

形状优化时希望结构的最大应力最小，取最大Von-Mises应力为研究对象

(28)

Von-Mises应力对控制顶点坐标的导数为

(29)

计算极值点，求得最大应力

(30)

式中，d为在u全局内最大应力点的控制顶点位移，A为由全局位移矢量转为局部位移矢量的变换矩阵，A在该处值为1，其它地方为0。局部处灵敏度为

(31)

式中，v为下列伴随方程的解。

(32)

4优化方法

本部分介绍优化方法和策略，确定设计变量，定义选择标准，提出相应算法。

4.1设计变量

在二维优化问题，首先，未裁剪表面的边界表面控制顶点坐标为设计变量，因为内部表面控制顶点不影响边界形状，所以，内部表面控制顶点不作为设计变量。一旦空洞生成，裁剪曲线的控制顶点坐标也作为设计变量了。控制顶点P的法向量n定义

(33)

式中，(ξP,ηP)是参数空间最接近裁剪点的控制顶点的坐标，t为切向量，k为单位向量。目标函数设计灵敏度与设计表面控制顶点法向移动有关，目标函数设计灵敏度为

(34)

4.2产生空洞的标准

对于式(21)的优化模型，定义选择标准为目标函数对约束的灵敏度

(35)

体积作为约束条件时，SC通常为正。当空洞产生时，体积就会变小。如果SC为负，没有改变约束，不可能再使目标函数性能提高。

SC有二种，一种是设计模型内产生空洞的选择标准SC洞，另一种是设计模型内外边界形状改变的选择标准SC形。目标函数的形状灵敏度和设计边界的控制顶点约束都要计算相应的SC形。比较二个选择标准SC形和SC洞能确定设计模型内部空洞是否产生。

若设计模型中，约束不变，设计控制顶点的变动而引起边界摄动，内部空洞产生，则

(36)

(37)

由式(36)和式(37)可得

(38)

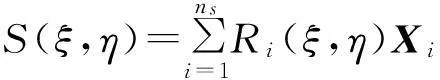
图7　在边界变动时表面设计控制顶点和选择标准 Fig.7 Surface design control points and their selestion criteria on boundary movement

4.3算法

(1)定义模型

(2)裁剪面分析

(3)灵敏度分析

(5)更新设计变量

(6)内部空洞是否合并?若合并返回(2)

(7)裁剪面分析

(8)收敛否?若不收敛，返回(3)

(9)收敛得优化结果

5应用实例

实例1

如图8所示为多载荷梁的结构优化计算模型，结构尺寸为200 mm×100 mm，弹性模量E=2.01×105MPa，泊松比ν=0.3，定义整个区域为设计域。在下端分别施加100 N、600 N、100 N三个集中力载荷，并在左下角约束了6个自由度，右下角约束了y方向的移动自由度。

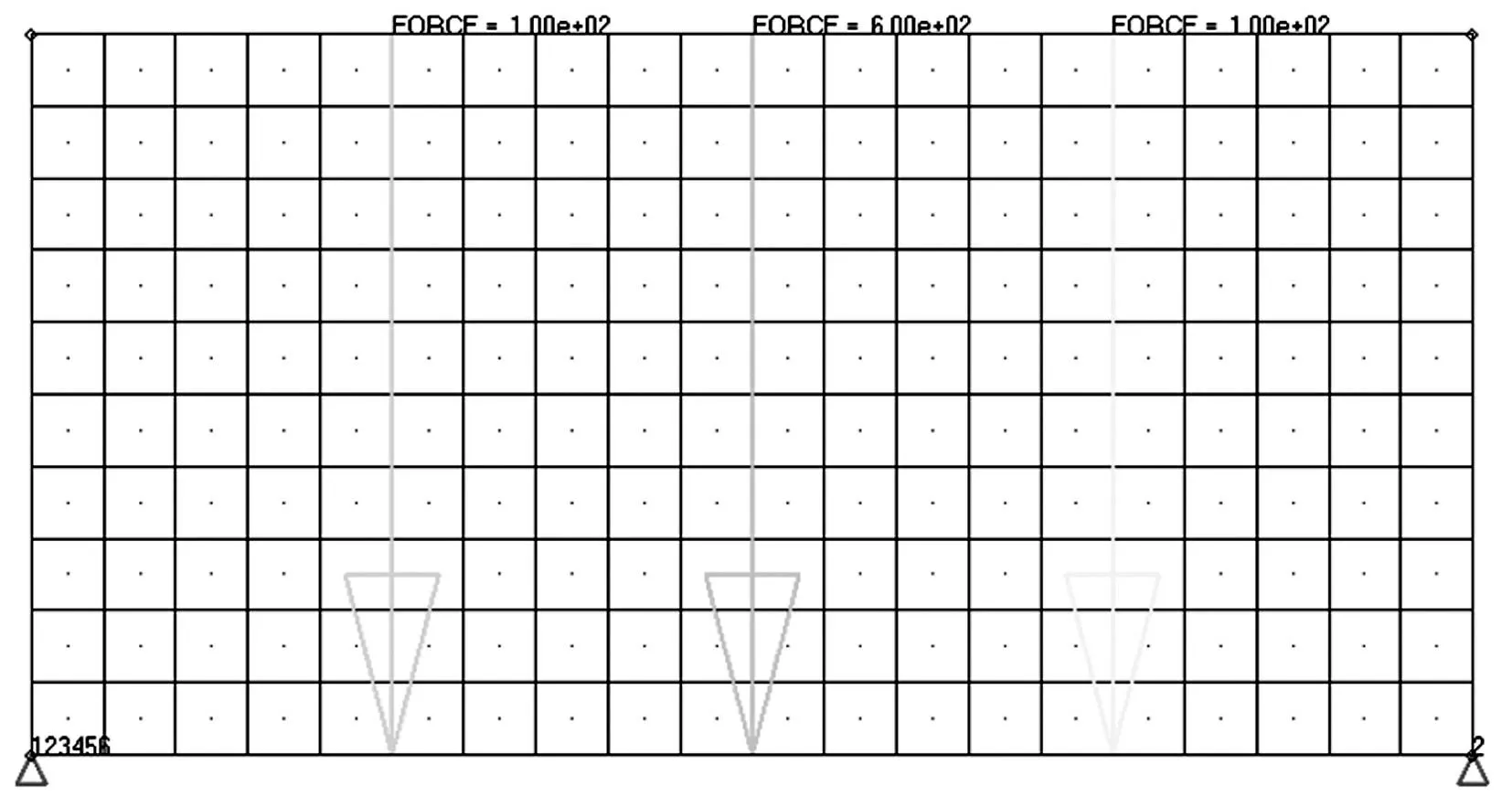
图8　优化模型 Fig.8 Optimization model

●表示设计面的控制顶点，■表示初始面的控制顶点 图9　物理空间初始面的控制顶点和设计面的控制顶点 Fig.9 Initial control pointsand design surface control points in physical area

如图9所示优化模型为二次B样条面，分为20×10个单元。在物理空间，以体积作为约束，以小方块表示初始表面的控制顶点，以小圆点表示设计面边界(顶端边界)的控制顶点，首先以设计面边界的控制顶点为设计变量，为了避免网格扭曲变形，二末端控制顶点允许沿垂直方向移动，其余控制顶点允许沿法向移动，其余边界无设计面控制顶点，但可由裁剪曲线按需要改变边界。按照上述优化方法进行优化，进行灵敏度分析，设计面边界的控制顶点(即设计变量)就会按计算的灵敏度方向移动，其余表面控制顶点会相应变动，尽管在小的区域控制顶点会较密集，但自适应使其不会相交。通过改变表面控制顶点坐标进行优化，直到由拓扑导数确定内部产生空洞位置为止，得如图10所示物理空间中表面的优化结果。

图10　物理空间中表面的优化结果 Fig.10 Optimal result in physical area

一旦空洞生成，裁剪曲线控制顶点的坐标也成为设计变量。下一步重点分析裁剪曲线控制顶点的灵敏度。

裁剪曲线方程为

(39)

式中，λ为曲线参数，ng为裁剪曲线控制顶点数量，裁剪曲线第k个控制顶点坐标为Pk=[pk,qk]。

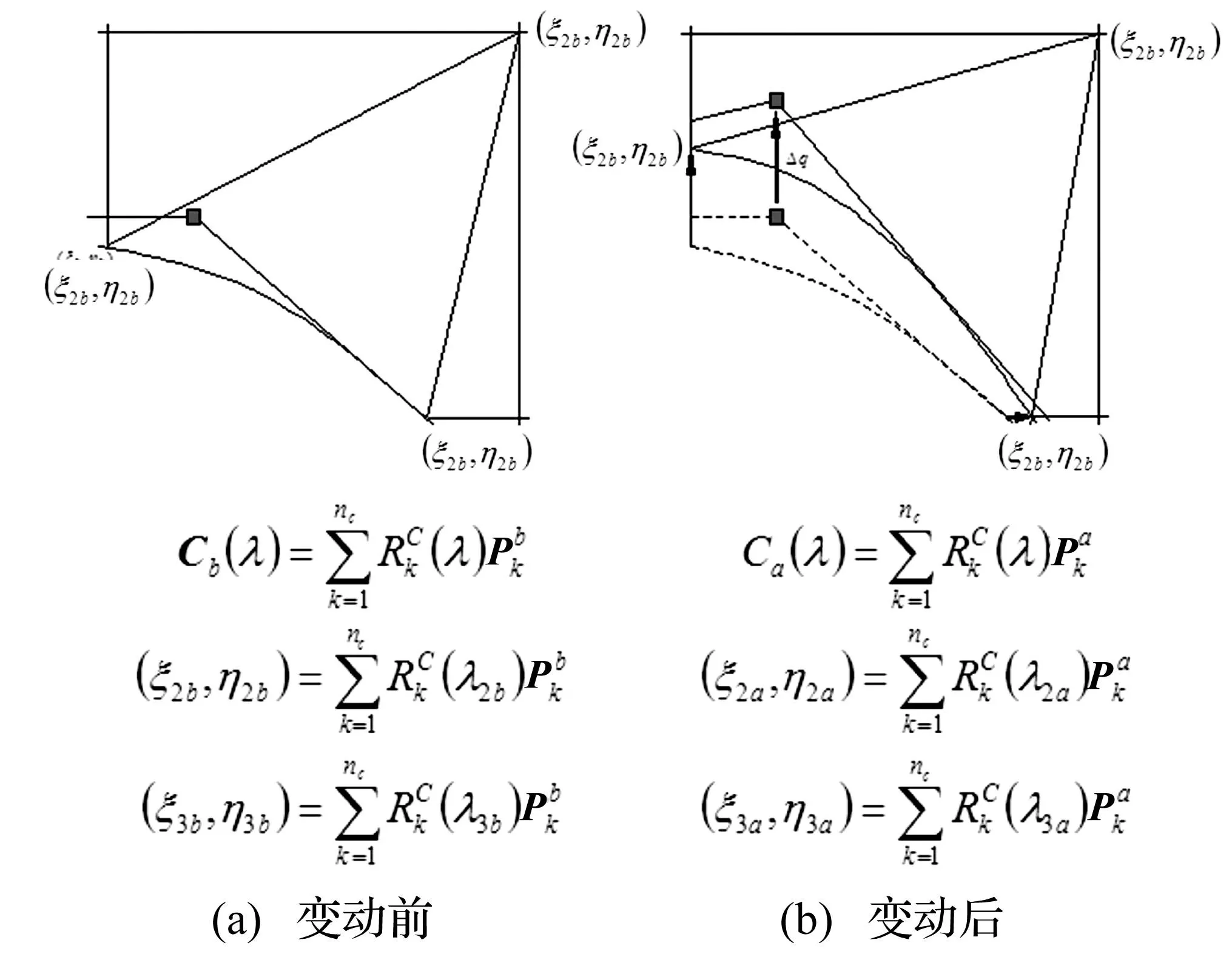
图11　交点灵敏度计算时裁剪曲线 控制顶点变动及其相应曲线参数 Fig.11 Movement of trimming curve control point for sensitivity compute of intersections and their corresponding curve parameters

图11说明由于裁剪曲线控制顶点摄动，二个交点及其相应参数变动情况。摄动前，二交点分别为(ξ2b,η2b)和(ξ3b,η3b)，其相应曲线参数分别为λ2b和λ3b。裁剪曲线控制顶点垂直摄动后，二交点分别变为(ξ2a,η2a)和(ξ3a,η3a)，其相应曲线参数也分别变为λ2a和λ3a。交点及其参数对曲线控制顶点摄动的灵敏度分别为

(40)

应变位移矩阵B对曲线控制顶点的灵敏度用Γ和G的灵敏度表示为

(41)

其中，Γ的灵敏度表示为

(42)

式中，

(43)

G对曲线控制顶点的灵敏度表示为

(44)

第k个基函数对曲线控制顶点的一阶导数用参数(ξ,η)灵敏度和基函数的二阶导数表示

(45)

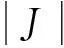
(46)

由式(14)可得雅可比灵敏度

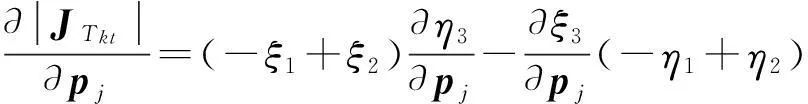
(47)

由式(17)计算曲线三角形积分单元的(ξ,η)灵敏度

(48)

由式(40)计算交点的灵敏度

(49)

由式(16)计算式(48)中参数α和β的灵敏度

(50)

由式(18)可得

(51)

其中

(52)

由式(39)可得裁剪曲线灵敏度

(53)

由式(15)可得曲线参数λ灵敏度

(54)

(55)

(56)

(57)

(58)

(59)

对裁剪曲线求偏导

(60)

它对曲线控制顶点的灵敏度为

(61)

由式(56)到式(61)可计算曲边三角形积分单元的式(55)雅可比行列式灵敏度。

图12 在参数空间中的模型Fig.12Modelintheparametricarea图13 在物理空间中裁剪曲线控制顶点Fig.13Controlpointsinthephysicalarea图14 在物理空间中选定裁剪曲线的详细信息Fig.14Detailedinformationofselectcurveinthephysicalarea

图15 物理空间中未裁剪表面的优化结果Fig.15Optimaluntrimmedresultinthephysicalarea图16 物理空间表面控制顶点和逐步细化积分单元Fig.16Controlpointsofdecomposedintegrationelementsinthephysicalarea图17 裁剪面分析应力云图(Von-Mises应力场)Fig.17Stresscontoursoftrimmingcurve

图18 裁剪优化结果Fig.18Optimaltrimmedresult图19 形状优化结果Fig.19Shapeoptimalresult图20 形状优化应力云图(Von-Mises应力场)Fig.20Stresscontoursofshapeoptimization

图16所示为在物理空间中的模型，显示适应表面控制顶点的敏度，图17所示为裁剪面分析应力云图(Von-Mises应力场)，图18所示为裁剪优化结果。

然后，再进行形状优化灵敏度分析，形状优化时希望结构的最大应力最小，取最大Von-Mises应力为研究对象,求Von-Mises应力对控制顶点坐标的导数，计算极值点，得优化形状，图19 所示为形状优化结果，图20形状优化应力云图。

实例2

如图21所示为单载荷梁的结构优化计算模型，结构尺寸为200 mm×100 mm，弹性模量E=2.01×105MPa，泊松比ν=0.3，定义整个区域为设计域。在右边缘下端施加一个100 N的载荷，并约束了左边缘6个自由度。

如图22所示优化模型为二次B样条面，分为20×10个单元。在物理空间，以体积作为约束，以小方块表示初始表面的控制顶点，以小圆点表示设计面边界(顶端边界)的控制顶点，首先以设计面边界的控制顶点为设计变量，为了避免网格扭曲变形，二末端控制顶点允许沿垂直方向移动，其余控制顶点允许沿法向移动，其余边界无设计面控制顶点，但可由裁剪曲线按需要改变边界。按照上述优化方法进行优化，进行灵敏度分析，设计面边界的控制顶点(即设计变量)就会按计算的灵敏度方向移动，其余表面控制顶点会相应变动，尽管在小的区域控制顶点会较密集，但自适应使其不会相交。通过改变表面控制顶点坐标进行优化，直到由拓扑导数确定内部产生空洞位置为止，空洞生成后，裁剪曲线控制顶点的坐标也成为设计变量，更新设计变量，外部边界和内部边界同时优化，物理空间和参数空间的拓扑结构同时相应改变。

图21 优化模型Fig.21Optimizationmodel图22 物理空间初始面的控制顶点和设计面的控制顶点Fig.22Initialcontrolpointsanddesignsurfacecontrolpointsinphysicalarea图23 在参数空间中的模型Fig.23Modelintheparametricarea

图24　在物理空间中裁剪曲线控制顶点 Fig.24 Control points in the physical area

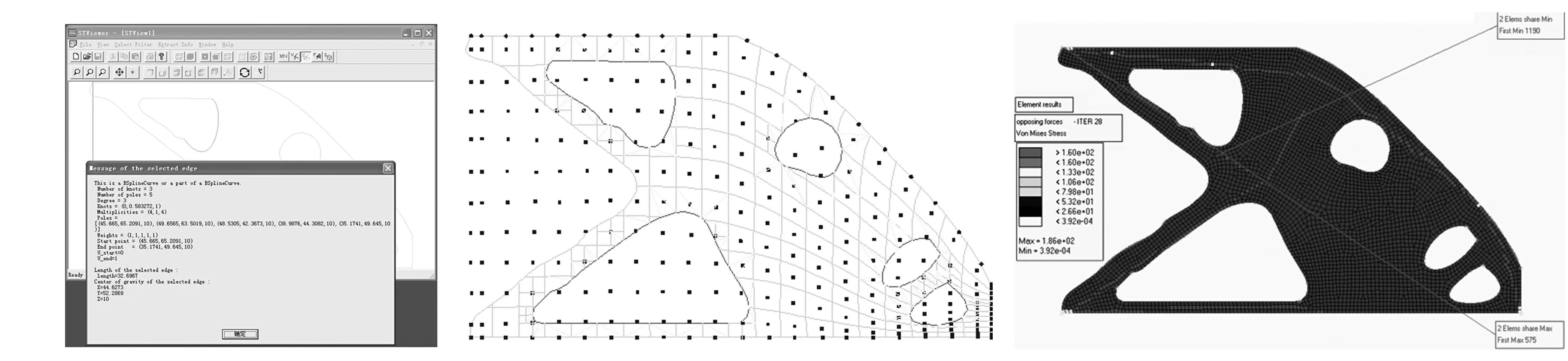
图25 在物理空间中选定裁剪曲线的详细信息Fig.25Detailedinformationofselectcurveinthephysicalarea图26 物理空间表面控制顶点和逐步细化积分单元Fig.26Controlpointsofdecomposedintegrationelementsinthephysicalarea图27 裁剪面分析应力云图(Von-Mises应力场)Fig.27Stresscontoursoftrimmingcurve

图26所示为在物理空间中的模型，显示适应表面控制顶点的敏度，图27所示为裁剪面分析应力云图(Von-Mises 应力场)，图28所示为裁剪优化结果。

然后，再进行形状优化灵敏度分析，形状优化时希望结构的最大应力最小，取最大Von-Mises应力为研究对象,求Von-Mises应力对控制顶点坐标的导数，计算极值点，得优化形状，图29 所示为形状优化结果，图30形状优化应力云图。

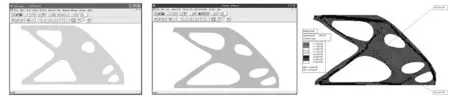
图28 裁剪优化结果Fig.28Optimaltrimmedresult图29 形状优化结果Fig.29Shapeoptimalresult图30 形状优化应力云图(Von-Mises应力场)Fig.30Stresscontoursofshapeoptimization

6结论

(1)本文探讨了将设计和分析、拓扑与形状优化双集成的基于等几何裁剪分析的连续体结构拓扑与形状集成优化设计方法，该方法将在CAD系统表达几何模型控制顶点和基函数的样条信息用于CAE，CAD、CAE和优化设计是同一个模型，实现其无缝集成。

(2)用B样条和裁剪曲线表示设计模型的内外边界，用裁剪面分析能方便处理复杂样条面，改变拓扑结构，设计结果不限定在初始的设计空间内。将未裁剪表面控制顶点坐标为设计变量，一旦空洞生成，裁剪曲线控制顶点坐标也作为设计变量，无需额外的设计变量参数。为了避免未裁剪面的几个网格发生畸变，将除了角点外的设计面控制顶点沿法线方向移动，确定产生合理裁剪曲线的选择标准使拓扑结构往更合理方向变动，结构变动时无需重新划分网格。

(3)建立了等几何裁剪曲线和表面的设计控制顶点灵敏度计算方法，优化过程中，内部的拓扑结构是灵活可变的，提出了内部空洞产生和合并算法，常规的优化方法，设计空间相关是一个不足，提出的样条优化很好解决了这个问题，在拓扑优化中，对常规网格相关载荷也较难处理，用提出的方法容易处理，在数字分析和优化中，转到CAD模型时，样条信息是一样的，消除后处理的工作量，同时优化拓扑结构和形状，典型实例表明所用方法的合理性和有效性。该方法容易扩展设计空间，方便分析处理，高度集成优化设计，高效可行，具有工程应用价值。

参考文献

[1]Huang X, Xie Y M. Evolutionary Topology Optimization of Continuum Structures: Methods and Application[M]. London: Springer, 2010.

[2]Bendsoe M P, Sigmund O. Topology optimization: theory, methods, and applications[M]. New York:Springer-Verlag, 2003.

[3]Qian X, Sigmund O.Isogeometric shape optimization of photonic crystals via Coons patches[J]. Computer Methods in Applied Mechanics and Engineering, 2011,200(25-28):2237-2255.

[4]程耿东，许林. 基于可靠度的结构优化的序列近似规划算法[J].计算力学学报，2006,23(6):641-646.

CHENG Geng-dong, XU Lin.Sequential approximate programming approach to reliability based structural optimization[J].Chinese Journal of Computational Mechanics 2006,23(6):641-646.

[5]Wang M Y, Wang X, Guo D. A level set method for structural topology optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(1-2): 227-246.

[6]Uhm T K, Kim K S, Seo Y D, et al. A locally refinable T-spline finite element method for CAD/CAE integration[J]. Structural Engineering and Mechanics, 2008,30(2):225-245.

[7]Wall W A, Frenzel M A, Cyron C. Isogeometric structural shape optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2008,197(33-40): 2976-2988.

[8]Dedè L, Borden M J, Hughes T J R.Isogeometric analysis for topology optimization with a phase field model[J].Archives of Computational Methods in Engineering,2012,19(3):427-465.

[9]Hassani B, Khanzadi M, Tavakkoli S M.An isogeometrical approach to structural topology optimization by optimality criteria[J]. Structural and Multidisciplinary Optimization, 2012,45(2):223-233.

[10]Lipton S, Evans J A, Bazilevs Y, et al. Robustness of isogeometric structural discretizations under severe mesh distortion[J]. Computer Methods in Applied Mechanics and Engineering 2010, 199(5-8): 357-373.

[11]Hassani B, Tavakkoli S M, Moghadam N Z.Application of isogeometric analysis in structural shape optimization[J].Scientia Iranica.2011,18(4):846-852.

[12]Hughes T J R, Cottrell J A, Bazilevs Y.Isogemetric analysis:CAD, finite element, NURBS,exact geometry and mesh refinement[J]. Computer Methods in Applied Mechanics and Engineering,2005,194(39-41):4135-4195.

[13]Cottrell J A, Reali A, Bazilevs Y, et al. Isogeometric analysis of structural vibrations[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(41-43):5257-5296.

[14]Auricchio F, Da Veiga L B, Hughes T J R, et al.Isogeometric collocation methods[J]. Mathematical Models and Methods in Applied Sciences, 2010, 20(11):2075-2107.

[15]Bazilevs Y, Da Veiga L B, Cottrell J,et al. Isogeometric analysis: approximation, stability and error estimates for h-refined meshes[J]. Mathematical Models and Methods in Applied Sciences, 2006, 16(7):1031-1090.

[16]Hughes T J R, Reali A, Sangalli G. Efficient quadrature for NURBS based isogeometric analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2010,199(5-8):301-313.

[17]Hughes T J R, The finite element method: linear static and dynamic finite element analysis[M]. Dover Publications, Mineola, New York:2000.

[18]Roh H Y, Cho M, Integration of geometric design and mechanical analysis using B-spline functions on surface[J]. International Journal for Numerical Methods in Engineering. 2005, 62(14):1927-1949.

[19]Li K, Qian X. Isogeometric analysis and shape optimization via boundary integral[J].Computer Aided Design,2011,43(11):1427-1437.

[20]Hesch C, Betsch P.Isogeometric analysis and domain decomposition methods[J].Computer Methods in Applied Mechanics and Engineering,2012,213-216:104-112.

[21]Qian X, Full analytical sensitivities in NURBS based isogeometric shape optimization[J]. Computer Methods in Applied Mechanics and Engineering.2010, 199(29-32):2059-2071.

[22]Seo Y D, Kim H J, Youn S K. Shape optimization and its extension to topological design based on isogeometric analysis[J]. International Journal of Solids and Structures. 2010, 47(11-12):1618-1640.

[23]Cea J, Garreau S, Guillaume P,et al. The shape and topological optimizations connection[J]. Computer Methods in Applied Mechanics and Engineering.2000,188(4):713-726.

[24]Manh N D, Evgrafov A, Gersborg A R,et al.Isogeometric shape optimization of vibrating membranes[J]. Computer Methods in Applied Mechanics and Engineering, 2011,200(13-16):1343-1353.

[25]Navarrina F, Gómez H,París J,et al.Isogeometric shape sensitivity analysis[J].WIT Transactions on the Built Environment,2012,125:119-130.

[26]Allaire G, Jouve F, Toader A M. Structural optimization using sensitivity analysis and a level set method[J]. Journal of Computational Physics. 2004,194(1):363-393.

[27]傅晓锦.连续体结构综合优化设计[J].机械工程学报，2012,48(1): 128-134.

FU Xiao-jin. Integration optimization design of continuum structure[J].Chinese Journal of Mechanical Engineering, 2012,48(1): 128-134.

[28]傅晓锦,卢炎麟.拓扑和形状集成优化设计[J].计算机集成制造系统，2008,14(6): 1041-1048.

FU Xiao-jin,LU Yan-lin. Integration of topology and shape optimization[J].Computer Integrated Manufacturing Systems, 2008,14(6): 1041-1048.

[29]施法中. 计算机辅助几何设计与非均匀有理B样条[M].北京：高等教育出版社，2001.8.

[30]Piegl L, Tiller W, The NURBS Book (2nd Edition)[M], Springer-Verlag Berlin Heidelberg, Germany: 1997.

[31]朱心雄. 自由曲线曲面造型[M].北京：科学出版社,2000.

[32]Cho S, Ha S H. Isogeometric shape design optimization: exact geometry and enhanced sensitivity[J]. Structural and Multidisciplinary Optimization. 2009, 38(1):53-70.

[33]Choi K K, Kim N H. Structural sensitivity analysis and optimization 2:nonlinear systems and applications[M]. New York: Springer, 2005.