基于MCKD和重分配小波尺度谱的旋转机械复合故障诊断研究

第一作者钟先友男，博士，讲师，1977年生

基于MCKD和重分配小波尺度谱的旋转机械复合故障诊断研究

钟先友，赵春华，陈保家，田红亮

(三峡大学水电机械设备设计与维护湖北省重点实验室，湖北宜昌443002)

摘要：针对强噪声环境下旋转机械复合故障信号难于提取与分离的问题，提出了基于最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution，MCKD)和重分配小波尺度谱的旋转机械故障诊断方法。机械信号中存在的噪声会降低重分配小波尺度谱的时频分布可读性，故先要对信号进行MCKD降噪，同时从振动信号中分离出各个故障成分，然后进行Hilbert变换得到包络成分，最后再对包络成分进行重分配小波尺度谱分析，根据尺度图中冲击成分的周期诊断转机械复合故障，算法仿真和应用实例验证了该方法的有效性。

关键词：最大相关峭度解卷积；重分配小波尺度谱；复合故障；最小熵解卷积

基金项目：国家自然科学基金资助项目(51205230, 51275273,51405264)

收稿日期：2014-09-12修改稿收到日期：2014-12-03

中图分类号:TH113.1；TN911.7

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.025

Abstract:Aiming at the problem that the rotating machinery composite faults signal is difficult to be extracted and segmented under strong noise background，a fault diagnosis method for rotating machinery based on maximum correlated kurtosis deconvolution (MCKD) and reassigned wavelet scalogram was proposed. The noise in the rotating machinery vibration signal would reduce the readability of its time-frequency representation，so the noise was reduced by using MCKD，and the fault components were separated from the vibration signal, and then the envelopes were obtained by Hilbert transform and analyzed with the reassigned wavelet scalogram. The composite faults of rotating machinery were diagnosed according to the periods of impulsire components in the scalogram. Some simulation and application examples validate the effectiveness of the method.

Rotating machinery fault diagnosis based on maximum correlation kurtosis deconvolution and reassigned wavelet scalogram

ZHONGXian-you，ZHAOChun-hua，CHENBao-jia，TIANHong-liang(Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance，China Three Gorges University, Yichang 443002, China)

Key words:maximum correlated kurtosis deconvolution; reassigned wavelet scalogram; composite fault; minimum entropy deconvolution

旋转机械的故障诊断对于减少经济损失和避免人员伤亡具有十分重要的意义。实际生产中旋转机械的故障通常往往表现为复合故障。国内外学者对旋转机械诊断方法进行了大量研究，但是绝大多数是对旋转机械的单一故障进行研究，旋转机械的复合故障诊断仍然是机械故障诊断的难点问题。Purushotham等[1]将小波分析与隐马尔科夫模型相结合，成功地实现了滚动轴承多种故障的分类。Sugumaran等[2]结合决策树和最接近支持矢量机，实现了对多种轴承故障的分类。雷亚国等[3]运用多征兆域特征集和多个分类器混合智能诊断模型对轴承复合故障进行了有效诊断。以上是通过分类的方法来实现对旋转机械复合故障的诊断，但合适的故障样本的获取不易。盲源分离[4-7]在旋转机械的复合故障中得到了应用，大多数机械故障源盲分离方法要求源信号满足非高斯非平稳且相互独立的假设，然而这种假设在机械设备故障诊断中往往是难以满足[8]；另外盲源分离往往需要对多个通道的信号进行分析，多个信号通道有时在现实中难以实现。因此，用尽量少的传感器诊断故障具有重要的工程意义。李蓉等[9]针对变转速下的齿轮箱中复合故障的故障特征提取，提出了一种基于线调频小波路径追踪算法与集合经验模式分解的齿轮箱复合故障诊断方法。杨杰等[10]提出了基于核形态成分分析的齿轮箱复合故障诊断方法。李辉等[11]对形态分量分析进行改进并成功地实现了的轴承多故障的特征提取。莫代一等[12]提出了基于并联双重Q因子的轴承复合故障诊断方法。

McDonald等[13]提出了最大相关峭度解卷积(MCKD)用于齿轮故障诊断，取得了良好的效果，但只是对单一故障进行诊断。重分配小波尺度谱具有较好的时频集中性和较少的干扰项，在旋转机械故障诊断领域得到了广泛的应用[14-15]，但是，重分配小波尺度谱的时频可读性对信号中的噪声敏感，为此，对信号进行重分配小波尺度谱分析之前采用最大相关峭度解卷积对故障信号进行降噪和分离，从而提高重分配小波尺度谱的时频可读性。基于上面的分析，本文结合MCKD、Hilbert变换和重分配小波尺度谱进行旋转机械的复合故障诊断。

1最大相关峭度解卷积原理

相关峭度定义为：

(1)

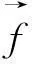
令

(2)

求解得到滤波器的结果通过矩阵形式表示如下：

(3)

其中：

r=[0T2T…mT]

(1)确定周期T、移位数M和滤波器的长度L；

(6)如果滤波前后信号的ΔCKm(T)>ε时，跳到第3步继续循环，否则停止递归。ε用来控制迭代终止的较小正数；

2重分配小波尺度谱

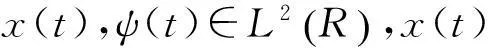
(4)

式中:a为尺度因子，b为平移因子，(t)为母小波，C为容许性条件，Wx(a,b;)为小波系数。由逆变换可知，信号x(t)的小波变换没有损失任何信息，变换是能量守恒的，因而下式成立:

(5)

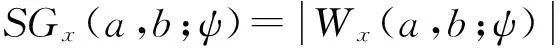
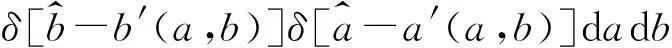
(6)

其中

(7)

(8)

(9)

重分配小波尺度谱通过对小波尺度谱能量重心的再分配，改善了尺度谱的集中性，在一定程度上消除了干扰项，使重分配后的尺度谱能更好地反映振动信号的时频特性。

3基于MCKD和重分配小波尺度谱的旋转机械故障诊断

基于MCKD和重分配小波尺度谱的旋转机械故障诊断的实现步骤如下：

(1)确定周期T，采用MCKD对信号进行处理，分离出各故障成分；

(2)对各故障成分采用Hilbert变换提取包络信号；

(3)利用重分配小波尺度谱对包络信号进行分析，根据尺度图中的冲击周期诊断旋转机械故障。

4仿真信号分析

带损伤的齿轮和轴承都会产生规律性的冲击信号[16]。为了验证本文方法在机械故障诊断中的有效性，对模拟机械冲击信号进行分析，模拟信号表达式为：

kT)]U(t-kT)+n(t),k=1,2,3…(10)

m(t)=A[1+B·cos(2πf1t)]

(11)

式中m(t)是冲击幅值，是幅值调制函数。f1是第一调制频率。T为故障冲击周期。f2是系统的固有频率。c为冲击信号衰减指数，U(t)为单位阶跃函数，n(t)为噪声。其中取f2为1 kHz，阻尼系数为c=0.1,n(t)=0,m(t)=1，设T1=1/100,T2=1/40，即两个冲击信号的冲击频率分别为100 Hz和40 Hz，采样频率fs=4 kHz，根据式(10)和式(11)可得两个冲击信号的时域波形如图1。将两个冲击信号叠加成复合信号，并添加Gauss白噪噪声，使得信噪比为-10 dB，其时域波形和频谱如图2。

图1　冲击信号的时域波形 Fig.1 The time domain of impact signal

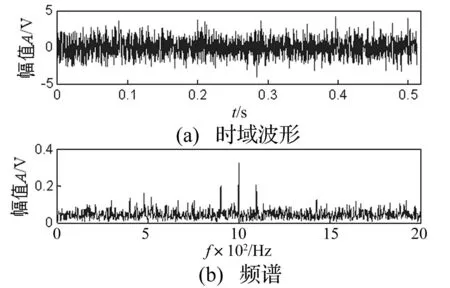
图2　复合信号的时域波形及频谱图 Fig.2 The time domain and frequency domain of composite signal

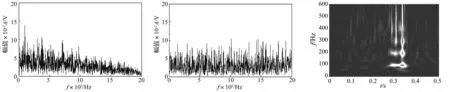
图3 复合信号的Hilbert包络谱Fig.3TheHilbertenvelopespectrumofcompositesignal图4 信号1的频谱Fig.4Thefrequencydomainofsignal1图5 包络信号1的重分配小波尺度谱Fig.5Reassignedwaveletscalogramofenvelopesignal1

对复合信号进行Hilbert变换并计算包络谱，如图3所示，冲击频率(100 Hz)可以识别，但是冲击频率(40 Hz)无法识别。

对于冲击频率为100 Hz的信号，fs=4 kHz，故T=fs/100=40，采用MCKD对信号进行处理，分离出信号1，图4是信号1的频谱图，从图中难以识别出故障特征信息。对信号1采用Hilbert变换提取包络信号1，图5是包络信号1的重分配小波尺度谱，从图中可以明显地看到特征频率成分100 Hz和200 Hz，即实现了对冲击成分1的提取。

对于冲击频率为40 Hz的信号，fs=4 kHz，故T=fs/40=100，采用MCKD对信号进行处理，分离出信号2，图6是信号2的频谱图，从图中难以识别出故障特征信息。对信号2采用Hilbert变换提取包络信号2，图7是包络信号2的重分配小波尺度谱，从图中可以看到明显的冲击，冲击之间的间隔为0.025，即冲击出现的频率为40 Hz，即实现了对冲击成分2的提取。

原复合信号的重分配小波尺度谱如图8所示，从图中无法提取故障特征。采用MED对信号进行处理，并采用Hilbert变换提取包络信号，图9是包络信号的重分配小波尺度谱，从图中可以看出MED未能提取出周期冲击脉冲特征。采用文献[8]中的方法，未能提取出周期冲击脉冲特征，究其原因，是本文的仿真信号信噪比低。

以上分析表明，MCKD可用于强噪环境下的故障特征提取。

图6　信号2的频谱 Fig.6 The frequency domain of signal 2

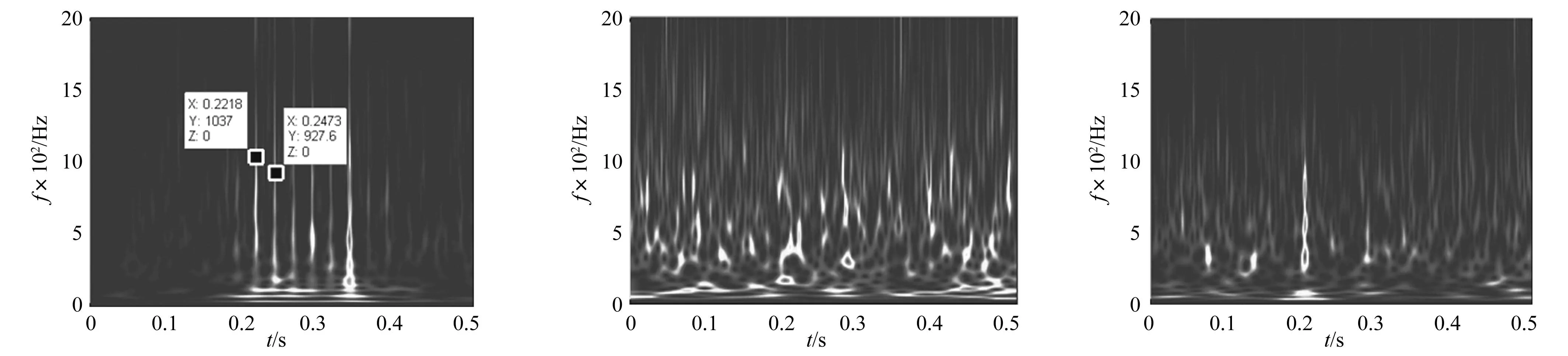
图7 包络信号2的重分配小波尺度谱Fig.7Reassignedwaveletscalogramofenvelopesignal2图8 复合信号的重分配小波尺度谱Fig.8Reassignedwaveletscalogramofcompositesignal图9 包络信号的重分配小波尺度谱Fig.9Reassignedwaveletscalogramofenvelopesignal

5工程应用

5.1空分机齿轮故障诊断

某西部化工厂空气分离机组通过齿轮箱增速带动压缩机，齿轮箱为一级传动，大齿轮91齿，转速5 840 r/min，即转频为97.3 Hz，小齿轮36齿，其转频约为246 Hz，采样频率fs= 7 872 Hz。图10是08年11月14日在增速箱高速轴垂直方向采集到的振动速度信号，对齿轮振动信号进行Hilbert变换计算包络谱，如图11所示，在图中80.72 Hz和641.9 Hz成分突出，但与故障特征频率(转频和啮合频率)无一对应，故从图中无法提取出齿轮故障的特征信息。

图10　空分机齿轮信号时域波形 Fig.10 The time domain of air separator gear signal

图11　空分机齿轮信号的包络谱 Fig.11 The envelope spectrum of air separator gear signal

对于转频97.3 Hz，对应T=7872/97.3≈82，运用MCKD对信号进行处理，分离出信号1，对信号1采用Hilbert变换提取包络信号1，图12是包络信号1的重分配小波尺度谱，从图中可以明显地看到特征频率97.85 Hz，与大齿轮的转频相近，表明大齿轮存在局部故障，在后来的开机检查中发现大齿轮严重磨损，如图13所示。对于转频246 Hz，对应T=7872/246≈32，采用MCKD对信号进行处理，分离出信号2，对信号2采用Hilbert变换提取包络信号2，图14是包络信号2的重分配小波尺度谱，从图中可以明显地看到特征频率成分246.5 Hz及其二倍频，与小齿轮的转频及二倍频相近，表明小齿轮存在局部故障，在开机检查中发现小齿轮也存在磨损。

图12 包络信号1的重分配小波尺度谱Fig.12Reassignedwaveletscalogramofenvelopesignal1图13 齿轮损坏图Fig.13Geardamagepicture图14 包络信号1的重分配小波尺度谱Fig.14Reassignedwaveletscalogramofenvelopesignal1

5.2轴承复合故障诊断

轴承振动信号采自轴承试验台，轴承为内外圈复合点蚀故障，轴承型号为6308，滚动体数量为8，节圆直径为65 mm，滚动体直径为15 mm，接触角为0°，电动机转速为1 165 r/min，采样频率为12 000 Hz，经计算得轴承外圈故障特征频率为59.7 Hz，内圈故障特征频率为95.5 Hz。图15为齿轮故障振动信号的时域波形和频谱图，从图中难以分辨出信号的具体特征。

对于外圈故障特征频率59.7 Hz，对应T=fs/59.7=12 000/59.7≈201，采用MCKD对复合故障信号进行处理，分离出信号1，对信号1采用Hilbert变换提取包络信号1，图16是包络信号1的重分配小波尺度谱，从图中可以看到明显的冲击，冲击之间的间隔约为0.017，即冲击出现的频率为58.8Hz，与轴承外圈故障特征频率59.7 Hz十分相近，即实现了轴承外圈故障特征的提取。对于内圈故障特征频率95.5 Hz，对应T=fs/95.5=12000/59.7≈126，采用MCKD对信号进行处理，分离出信号2，对信号2采用Hilbert变换提取包络信号2，图17是包络信号2的重分配小波尺度谱，从图中可以明显地看到频率成分96.87 Hz和190.8 Hz，分别与内圈故障特征频率95.5 Hz及其二倍频相近，即实现了轴承内圈故障特征的提取。

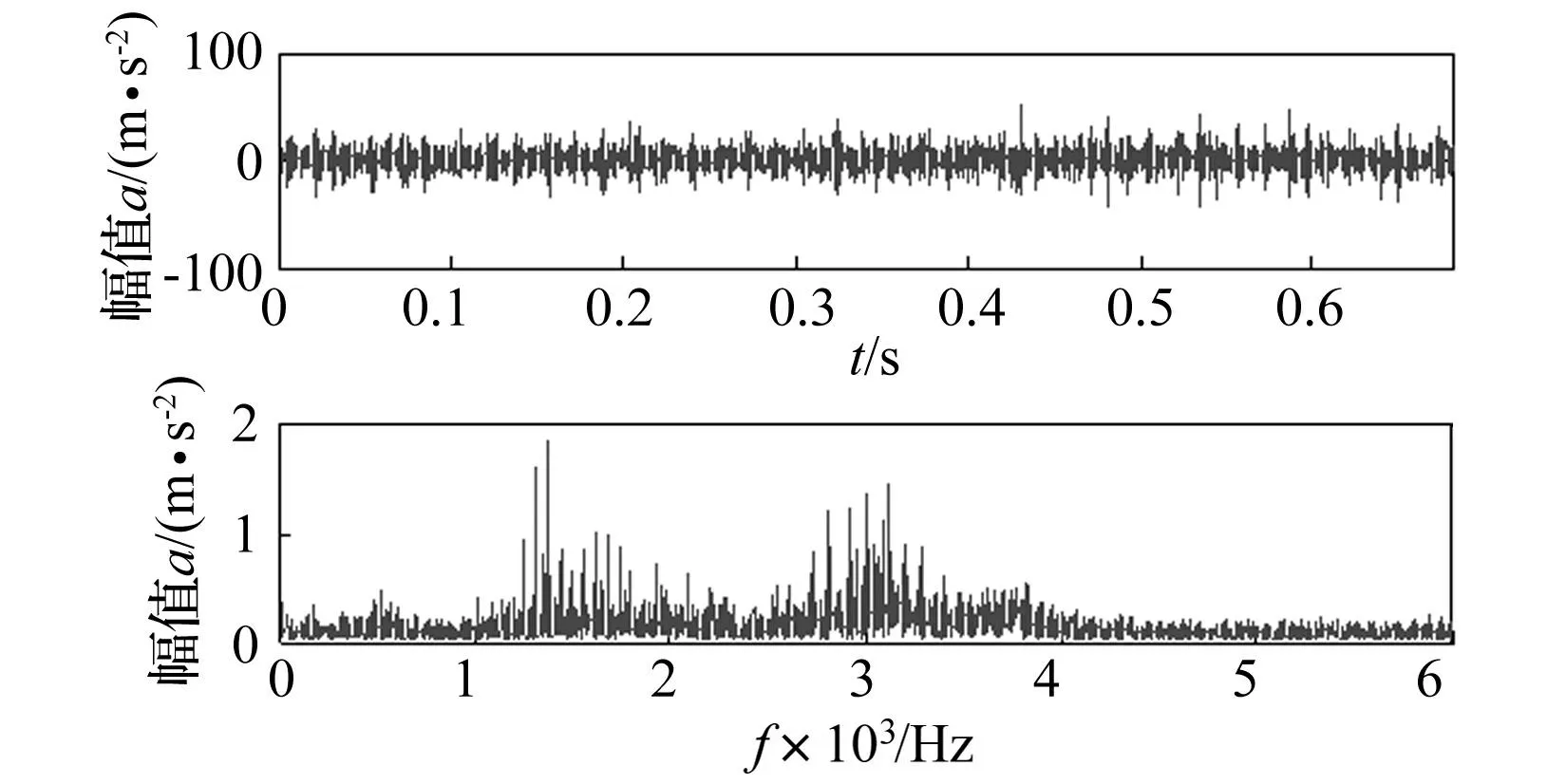
图15　轴承信号的时域波形及频谱图 Fig.15 The time domain and frequency domain of bearing signal

对轴承复合故障信号不进行MCKD降噪，直接求其重分配小波尺度谱，从图中无法提取故障特征，限于篇幅，不作详细分析。

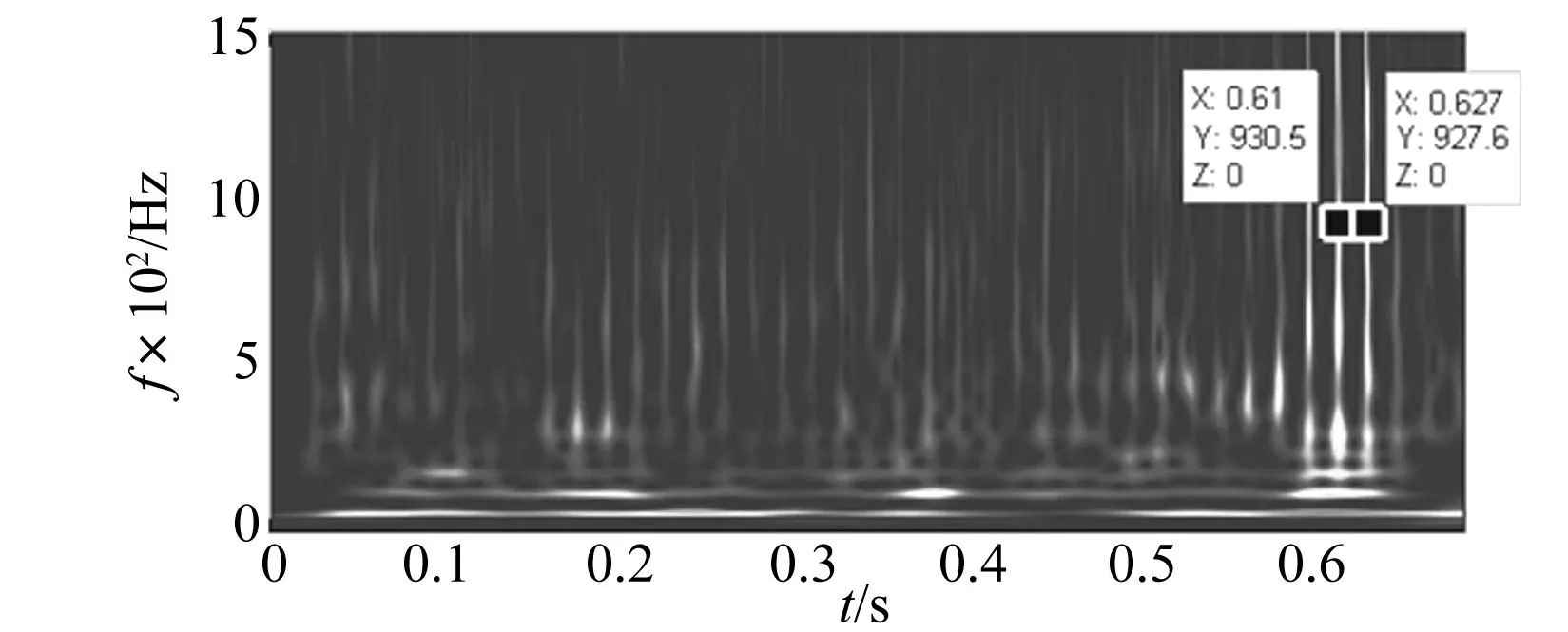
图16　包络信号1的重分配小波尺度谱 Fig.16 Reassigned wavelet scalogram of envelope signal 1

图17　包络信号2的重分配小波尺度谱 Fig.17 Reassigned wavelet scalogram of envelope signal 2

6结论

通过仿真及实际工程应用实例验证表明，采用基于MCKD降噪、Hilbert变换和重分配小波尺度谱的方法进行旋转机械的复合故障诊断是可行的。本文得到的主要结论有:

(1)MCKD降噪能力比MED强，可用于强噪环境下的旋转机械故障特征提取；

(2)MCKD降噪的同时，实现了复合故障信号的分离，本文所提方法只需要对一个通道的信号进行分析，简单易于实现，克服了盲源分离使用的缺陷，为旋转机械复合故障诊断提供了一种新方法，具有较高的工程应用价值。

参考文献

[1]Purushotham V, Narayanana S, Prasad A N. Multi-fault diagnosis of rolling bearing elements using wavelet analysis and hidden Markov model based fault recognition[J]. Journal of NDT & E International, 2005, 38：654-664.

[2]Sugumaran V, Muralidharan V, Ramachandran K I. Feature selection using decision tree and classification through proximal support vector machine for fault diagnostics of roller bearing[J]. Mechanical Systems and Signal Processing，2007，21(2)：930-942.

[3]雷亚国，何正嘉，訾艳阳. 基于混合智能新模型的故障诊断[J]. 机械工程学报，2008，44(7)：112-117.

LEI Ya-guo, HE Zheng-jia, ZI Yan-yang. Fault diagnosis based on novel hybrid intelligent model[J]. Chinese Journal of Mechanical Engineering, 2008，44(7)：112-117.

[4]Antoni J. Blind separation of vibration components: principles and demonstrations[J]. Mechanical Systems and Signal Processing, 2005, 19(6): 1166-1180.

[5]叶红仙，杨世锡，杨将新. 多振源卷积混合的时域盲源分离算法[J]. 机械工程学报，2009，45(1)：189-194.

YE Hong-xian，YANG Shi-xi，YANG Jiang-xin. Temproral blind source separation algorithm for convolution mixtures with multi vibration sources[J]. Journal of Mechanical Engineering，2009，45(1)：189-194.

[6]WANG Jun-feng，SHI Tie-lin，HE Ling-song，et al. Frequency overlapped signal identification using blind source separation[J]. Chinese Journal of Mechanical Engineering，2006，19(2)：286-289.

[7]王宇, 迟毅林, 伍星, 等. 基于盲信号处理的机械噪声监测与故障诊断[J].振动与冲击, 2009, 28(6): 32-41.

WANG Yu, CHI Yi-lin, WU Xing, et al. Machine noise monitoring and fault diagnosis based on blind signal processing[J]. Journal of Vibration and Shock, 2009, 28(6): 32-41.

[8]李志农, 吕亚平, 范涛, 等. 基于经验模态分解的机械故障欠定盲源分离方法[J]. 航空动力学报, 2009, 24(8): 1886-1892.

LI Zhi-nong, LÜ Ya-ping, FAN Tao, et al. Underdetermined blind source separation method of machine faults based on empirical mode decomposition[J]. Journal of Aerospace Power, 2009, 24(8): 1886-1892.

[9]李蓉，于德介，陈向民,等. 基于线调频小波路径追踪算法与EEMD的齿轮箱复合故障诊断方法[J].振动与冲击，2014, 33 (3): 51-56.

LI Rong，YU De-jie，CHEN Xiang-min, et al. A compound fault diagnosis method for gearboxes based on chirplet path pursuit and EEMD[J]. Journal of Vibration and Shock, 2014, 33 (3): 51-56.

[10]杨杰, 郑海起, 关贞珍,等. 基于核形态成分分析的齿轮箱复合故障诊断研究[J]. 振动与冲击，2012，31(10): 97-101.

YANG Jie，ZHENG Hai-qi，GUAN Zhen-zhen, et al. Compound fault diagnosis for gearbox based on kernel morphological component analysis[J]. Journal of Vibration and Shock, 2012，31 (10): 97-101.

[11]李辉，郑海起，唐力伟. 基于改进形态分量分析的齿轮箱轴承多故障诊断研究[J]. 振动与冲击，2012，31(12): 135-140.

LI Hui，ZHENG Hai-qi，TANG Li-wei. Bearing multi-fault diagnosis based on improved morphological component analysis[J]. Journal of Vibration and Shock, 2012，31(12): 135-140.

[12]莫代一，崔玲丽，王婧，等. 并联双重Q因子在齿轮箱复合故障净化提取与盲分离中的应用[J].仪器仪表学报, 2013，34(9)：273-279.

MO Dai-yi，CUI Ling-li，WANG Jing, et al. Application of parallel dual-Q-factors in extraction and blind separation of gearbox composite faults[J].Chinese Journal of Scientific Instrument, 2013，34(9)：273-279.

[13]McDonald G L，Qing Z，Zuo M J. Maximum correlated Kurtosis deconvolution and application on gear tooth chip fault detection[J]. Mechanical Systems and Signal Processing，2012，33：237-255.

[14]廖传军，李学军，刘德顺．小波再分配尺度谱在声发射信号特征提取中的应用[J]．机械工程学报，2009，45(2)：273-279.

LIAO Chuan-jun，LI Xue-jun，LIU De-shun．Application of reasigned wavelet scalngram in feature extraction based on aeoustic emission signal[J]．Journal of Mechanical Engineering，2009，45(2)：273-279.

[15]陈向民，于德介，李蓉. 基于信号共振稀疏分解与重分配小波尺度谱的转子碰摩故障诊断方法[J].振动与冲击，2013, 32 (13): 27-33.

CHEN Xiang-min，YU De-jie，LI Rong. Rub-impact diagnosis of rotors with resonance-based sparse signal decomposition and reassigned wavelet scalogram[J]. Journal of Vibration and Shock, 2013, 32 (13): 27-33.

[16]WANG Xiao-dong，ZI Yan-yang，HE Zheng-jia. Multiwavelet construction via an adaptive symmetric lifting scheme and its applications for rotating machinery fault diagnosis[J]. Measurement Science and Technology，2009，20：04103.