基于改进交叉模型交叉模态法的局部损伤识别方法

第一作者占超男，硕士生，1990年生

通信作者李东升男，副教授，1972年生

邮箱：dsli@dlut.edu.cn

基于改进交叉模型交叉模态法的局部损伤识别方法

占超， 李东升， 任亮， 李宏男

(大连理工大学海岸及近海工程国家重点实验室，辽宁大连116024)

摘要：传统的交叉模型交叉模态(CMCM)法由于其核心矩阵的缺秩使其在全局修正时的解不唯一，为得到唯一解必须人为假定约束。以往利用CMCM法进行损伤识别的研究中，通常将损伤前后质量保持不变作为约束求得各单元刚度的修正量，然后将刚度的下降作为判断损伤的依据。然而，结构在极端运营条件下质量的变化也是损伤的一种。为此，对传统的CMCM法进行了改进，提出了以下的改进方法：首先，由基准状态下的有限元模型和损伤后实测的结构低阶模态信息求得核心矩阵，将核心矩阵最小奇异值对应的右奇异向量作为损伤指示向量(DIV)；然后，基于损伤的局部性利用聚类分析算法自动识别DIV中的异常元素，将异常元素作为损伤定位的依据；最后，由DIV估计各单元质量和刚度的损伤程度。改进后方法的优势在于：无需人为主观地添加约束即可一次性求出结构各单元质量和刚度损伤前后的变化，避免了错误或不准确的假设给损伤识别结果带来的误差。通过数值实验对该改进方法的可行性、鲁棒性以及损伤敏感性进行了研究，并通过美国洛斯阿拉莫斯国家实验室(LANL)的一个4自由度板柱结构振动台实验对改进方法的有效性做了进一步的验证。

关键词：损伤识别； 全局修正； 交叉模型交叉模态法； 结构健康监测

收稿日期：2014-01-02修改稿收到日期：2014-04-03

中图分类号:TP206+.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.021

Abstract:Since the core matrix in the traditional cross-model cross-mode(CMCM) method is rank-deficient, constraints must be applied artificially for getting a unique solution in a complete model-updating situation. In previous damage identification researches based on the CMCM method, structural masses are often supposed to be unchanged for getting the updated coefficients of stiffness, and the reduction of stiffness is regarded as an indicator of damage. However, elemental mass changes under operational conditions are obviously a kind of damages. For detecting damage more effectively, the traditional CMCM method was improved, and an improved method was proposed as follows: evaluate the core matrix from the finite element model under the baseline condition and the measured modal data after damage and take the right singular vector corresponding to the least singular value of the core matrix as a damage indication vector(DIV); identify the abnormal elements in the DIV by using cluster analysis algorithm based on the assumption that damage appears locally and locate damage based on these abnormal elements; derive the extent of damage for each elemental mass and stiffness from the DIV. The advantage of the improved method is its ability to solve the mass and stiffness changes before and after damage for all elements without artificial constraints, thus the error of damage identification caused by imprecise or wrong constraints vanishes. The improved method’s practicability, robustness, and sensitivity to damage were analysed via a numerical simulation, and its effectiveness is further verified by virtue of the experiments on a 4 degrees of freedom test-bed structure done at the Los Alamos National Laboratory.

Local damage identification approach based on improved cross-model cross-mode method

ZHANChao,LIDong-sheng,RENLiang,LIHong-nan(State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024,China)

Key words:damage identification; complete-updating; cross-modal cross-mode; structural health monitoring

随着我国经济的不断发展，大量土木工程结构(尤其是高层建筑和大跨桥梁)伴随着人们的需要如雨后春笋般涌现。这些结构在以后的服役过程中，由于各种因素(如地震、材料锈蚀等)某些构件往往会出现损伤。损伤的存在势必会降低结构的使用性能，放任损伤的加剧甚至可能引发重大的土木工程结构事故(如桥梁的突然折断、房屋的骤然倒塌等)，从而造成重大的人员伤亡和财产损失。因此，对重大工程结构的性能进行监测和诊断，及时发现结构的损伤，对可能出现的灾害进行预测并对结构的安全性能进行正确的评价，具有极其重要的意义，同时也是现代工程的迫切要求和土木工程学科发展的一个重要领域[1]。

结构健康监测和损伤识别近几十年来在硬件和理论上均有很大进展[2]，其中基于模型修正的损伤识别方法受到诸多学者的关注[3]。该类方法的基本思想为根据健康状态下的实测振动数据对结构的初始有限元模型进行修正，得到基准模型；结构损伤后，由损伤状态下的实测振动数据对基准模型进行修正，则损伤前后各单元模型参数的变化即反映出损伤的位置和程度。

传统的模型修正方法[5]主要有：利用模态信息的矩阵直接修正法、利用模态信息的迭代修正法和利用实测频响函数的修正法等。这些方法或多或少存在各种缺点，比如直接修正法修正后的质量、刚度矩阵无法保证原有的对称性、稀疏性、和正定性，缺乏物理意义；迭代修正法存在解的收敛性以及迭代过程中的误差累计问题，并且计算量较大；而频响函数修正法的修正参数估计为有偏估计。为了克服传统方法的不足，近年来不断有学者提出新的模型修正方法。Doebling等[6]提出通过敏感性分析得到单元连接矩阵，然后由最小秩法求出单元刚度参数的扰动量，并使修正后的刚度矩阵保持了原有的单元连接形式；Kaouk等[7]提出将模型修正分为两步，即先进行误差定位，再使用最小秩扰动法对结构质量、阻尼、刚度矩阵同时修正；侯吉林[8]提出基于局部模态的约束子结构模态修正法，并对此进行了系统地研究。

Hu等[9]提出了交叉模型交叉模态(CMCM)算法。该方法可以根据测得的有限低阶模态信息对单元质量和单元刚度矩阵同时修正，而且无需模态配对，对振型没有同比例要求，是一种直接的物理属性修正方法[10]。本文先对传统的CMCM法推导过程进行简要介绍；然后指出其中的不足并提出改进方法；接着通过一个数值实验对改进方法的可行性、鲁棒性和损伤敏感性进行研究；最后通过美国洛斯阿拉莫斯国家实验室(LANL)的一个4自由度板柱结构实验对改进方法的可行性做进一步验证。

1交叉模型交叉模态法

记有限元模型的刚度和质量矩阵分别为K和M，则

KΦ=MΦΛ

(1)

式中Φ为有限元模型振型矩阵，Λ为与各振型对应的圆频率的平方值构成的Ni阶对角阵。

类似式(1)，对于实际结构有

K*Φ*=M*Φ*Λ*

(2)

式中，K*和M*分别为实际结构的刚度和质量阵，Φ*实测振型矩阵，Λ*为实测圆频率的平方值构成的Nj阶对角阵。

式(2)等号两边同时左乘的Φ转置，即

ΦTK*Φ*=ΦTM*Φ*Λ*

(3)

假设实际结构的刚度和质量矩阵满足下列方程，

(4)

式中Kn与Mn分别为在整体坐标系下标号为n的单元刚度和单元质量矩阵，αn和βn分别为n号单元刚度矩阵修正系数和n号单元质量矩阵修正系数，NK和NM分别为单元刚度矩阵和单元质量矩阵的个数。

将式(4)代入式(3)，可得

(5)

式中

(6)

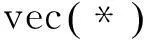
式(5)可以写成如下矩阵形式，

Gγ=f

(7)

式中

(8)

式(7)中矩阵G的行数，亦方程数Nm=NiNj；其列数，亦未知数个数Nu=NK+NM。由于矩阵G是CMCM算法的核心部分，因此也被称为核心矩阵[11-12]。需要指出的是，当实测模态测得足够准时，即使式(7)中方程数Nm大于未知数个数Nu，由于G的缺秩，式(7)仍会出现解不唯一的情况。要想得到唯一解，必须添加约束。假设约束方程如下，

(9)

若假设结构质量保持不变，则

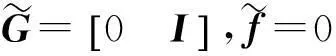
(10)

式中,I为维数为NM的单位方阵。将式(7)与式(10)合并，即得

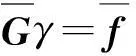
(11)

式中

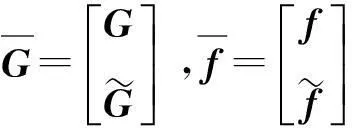
(12)

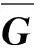
(13)

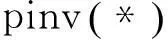
2改进的CMCM局部损伤识别法

在第1节介绍的传统CMCM法中，由于核心矩阵G的缺秩，使其在全局修正时解不唯一。要想得到唯一解，至少需要人为地添加一个约束。错误或者不精确的约束都可能会引起传统CMCM法修正结果出现误差。以往在对基于CMCM法的损伤识别研究中，往往假设各单元质量保持不变，而仅对各单元刚度进行修正，并以单元刚度的下降作为损伤判断的依据。然而，结构在极端运营条件下质量的变化(例如暴雪导致房屋顶层质量的显著增加等)也是损伤的一种。本节对传统CMCM法的推导过程稍加变动，提出改进的CMCM局部损伤识别法，如下：

假设损伤后刚度、质量阵K*和M*满足下列关系

(14)

式中ηn和εn分别为n号单元刚度矩阵和n号单元质量矩阵的“损伤比”，与式(4)中的αn和βn具有如下关系

ηn=1+αn，εn=1+βn

(15)

将式(14)代入式(3)，可得

(16)

将式(16)写成矩阵形式

Gv=0

(17)

其中Cn、Dn和G分别同式(6)和式(8)的定义。v定义如下

(18)

向量v的前半段和后半段分别记录了各单元刚度、质量损伤前后的比值，求得了v即实现了对结构参数损伤前后变化的全面了解。由式(17)可见，只要v有解，核心矩阵G必缺秩，v必有无穷多个解。求解v的问题即化为求解G的零空间的问题。

数学上往往采用奇异值分解的方法求解一个矩阵的零空间，即

G=USVT

(19)

式中S为Nu×Nu的对角矩阵，其对角线上记录了G的Nu个从大到小排列的奇异值s1,s2,…,sNu；U(Nm×Nu)和V(Nu×Nu)中各列向量分别称为G的各奇异值对应的左奇异向量和右奇异向量，并满足

UTUINu，VTV=INu

(20)

则奇异值s1,s2,…,sNu中0奇异值对应的右奇异向量即为零空间的基。

然而，由于仪器的内部噪声、计算机的舍入误差、环境噪声等因素，实际测得的模态中含有噪声而使得G趋于满秩，即所有奇异值均大于0。为此，我们取奇异值中最小的值sNu对应的右奇异向量作为解v的基，记为v*(v*满足v*Tv*=1)。

v与v*间满足倍数关系，即v=av*，其中a为待定系数。我们知道，损伤是一种典型的局部现象，两次动力测试中结构大部分的参数应该基本保持不变，只有损伤处参数会有较显著的变化，即：v中大部分元素都应该近似等于1，对应地v*中大部分元素应处于同一水平；损伤情况下v*中会出现少数异常元素，表现在与其他正常元素不在同一水平线上。v*中的异常元素可以作为损伤定位的依据。由于向量v*中包含结构的损伤信息，我们又称v*为损伤指示向量(Damage Indication Vector,DIV)。DIV中正常元素和异常元素的划分可以通过聚类分析算法[13]自动实现。聚类分析能够从样本数据出发，计算样本之间的空间距离，根据样本彼此间的亲疏关系，对样本进行自动分类。

(21)

(22)

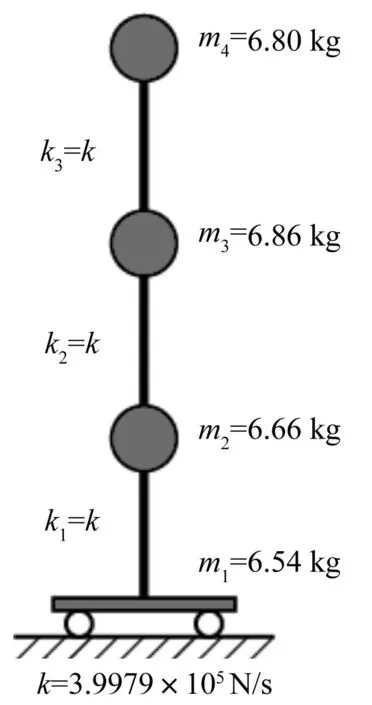
图1　四自由度链式 结构(数值实验) Fig.1 4-DOF chain-like system (for numerical simulation)

则av*即为我们对解v的估计，(av*-1)×100%即为我们对各单元刚度、质量损伤程度的估计。

3数值实验

3.1改进方法的可行性

本小节通过数值实验对第2节中改进方法的可行性进行说明。如图1所示一四自由度链式结构，底层柱与小车相连，结构整体可以在水平地面上自由滑动。各集中质量仅考虑其在水平方向上的运动。各层质量、小车质量以及各层柱的水平刚度如图中所示。实验中，结构的单处损伤通过将第一层的层间刚度k1折减50%实现；多处损伤工况下则将第二层的层间刚度k2折减20%，并将第一层的集中质量增加20%以模拟极端运营条件下质量的增加。数值实验中损伤状态下的模态是通过损伤后的有限元模型直接计算得到的。结构基准状态下的模态和损伤状态下的“实测”模态分别如表1和表2所示。结构的第一阶模态为平动模态，在表中不予显示。

表1　基准状态下有限元模型的模态

将表1和表2中的模态数据代入式(17)，即可求得损伤指示向量(DIV)，进而求得损伤位置和程度。无噪声情况下，单损伤工况和多损失工况的损伤识别结果如图2所示。图中可见，无论是单损伤工况还是多损伤工况下，DIV中异常元素均正确指示出损伤位置。单损伤工况中，η1被标记为异常元素，表明一号单元刚度出现异常；多损伤工况中，η2和ε2均被标记为异常，表明二号单元刚度以及二号单元质量(即图1中一层质量)出现了异常。两种工况下，损伤程度识别值均与预设值均很好地吻合，从而说明改进方法可行。

表2　损伤状态下的结构模态

图2　损伤识别结果(数值实验) Fig.2 The results of damage identification(numerical simulation)

3.2改进方法的鲁棒性和损伤敏感性

有关小损伤的识别一直是损伤识别中的难点。小损伤一方面对结构整体参数影响不大，难以从结构的动力响应信号中辨别；另一方面又对结构安全造成隐患，可能随时发展成大损伤进而导致结构构件失效甚至是结构整体的破坏。同时，实际工程中来自方方面面的噪音也对损伤的正确识别造成困难。本小节以多损伤工况(图1中第二层层间刚度折减y%，第一层集中质量增加y%，y为损伤程度)为例，对改进方法的鲁棒性和损伤敏感性进行研究。

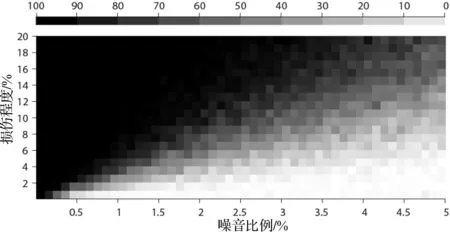
图3　改进方法识别性能灰度图 Fig.3 The grayscale of the improved method’s performance

我们以实测模态中的噪声比例x为横轴(分辨率0.1%)，以多损伤工况中的损伤程度y为纵轴(分辨率1%)，作出改进方法的识别性能灰度图，如图 3所示。图中各点(共50×20个点)均重复实验100次。每次实验中，首先由该点纵坐标对应的损伤程度求得对应的损伤有限元模型和损伤后的模态数据，然后在模拟的振型中加入该点横坐标对应比例的比例噪声，接着由含噪声的模态数据利用改进方法求得DIV，若DIV正确指示出了损伤位置，则记为一次成功的损伤识别。100次实验中，成功识别次数z越多，则识别性能越好，在图中对应的颜色也就越深。图中可以看到，识别性能随着损伤程度的减小和噪音比例的增大而变差。无噪声条件下，任意程度的损伤均可准确识别； 1%比例噪声下，改进方法可以对10%以上的损伤准确定位(z>95)；而在5%的比例噪声下，小损伤(y<5)的识别则完全无法实现。

4实验室实验

为进一步证实改进方法的可行性，本节对LANL实验室的一个4自由度板柱结构振动台实验数据[14-15]进行分析，并利用改进方法对预设的损伤进行识别。实验装置如图4所示。三层“楼板”和“基础”均为铝制金属板(30.5 cm×30.5 cm×2.5 cm)，彼此通过四根铝柱使用螺栓连接。“基础”被限制在轨道上使其仅可以在x方向上滑动。激振器采用(20 Hz~150 Hz)的限带白噪声对“基础”进行激励。结构上共安装5个传感器(通道1用于测量激振器对“基础”施加的力，通道2、3、4、5分别用于测量“基础”和一、二、三层“楼板”的加速度响应)，各传感器采样频率均为320 Hz，采样数目为8 192个。实验中将损伤归为两类，一类是线性损伤，另一类是非线性损伤。线性损伤通过在楼板或基础上添加集中质量块、替换某层的一根或两根铝柱(替换后的铝柱的横截面面积为原始的一半)以减小层间刚度来实现；非线性损伤[16]则通过调节顶层悬挂铝柱和安装在第二层楼板上的“碰撞器”之间的间距，在动荷载下二者之间不同程度的相互碰撞来模拟。本文仅对其中的线性损伤数据进行分析，如表3[17]所示。结构基准状态下的各传感器时程如图5所示。

图4　LANL 4自由度振动台试验装置图 Fig.3 Experiment setup for 4-DOF test-bed structure in LANL

表3　实验分组表 [17]

图5　基准状态下各传感器所测信号时程 Fig.5 Time histories of signals in each sensor under baseline condition

我们将激振器施加的力作为系统输入，将“基础”和各层“楼板”的加速度信号作为系统输出，使用OKID[18](Observer Kalman filter IDentification)算法进行模态识别。由于实测信号中的噪音和算法阶数的不同取值，测得的模态中含有虚假模态和计算模态，即非物理模态。模态分析中可以通过稳态图[19]的方法鉴别物理模态和非物理模态。与非物理模态不同的是，物理模态不会随算法阶数的增加而变化，因而在稳态图中呈现近乎一条直线。图6为基准状态下模态识别的稳态图。图中每个实心点对应一个识别的模态(为了使稳态图更加清晰，我们滤去了阻尼比大于5%的模态)；点画线为力对第三层楼板加速度的频响函数的幅值。图中可见，不同算法阶数下物理模态的频率具有较好的一致性，如虚线所示。限于篇幅，损伤状态下各传感器的时程和稳态图不再列出。不同工况下测得的模态具体数值见表 4。结构的有限元模型参数与数值实验中图1所示的各参数相同。将表4中基准状态下的实测模态与表1中的有限元模态相对比，可以发现二者比较吻合，但仍略有差异。为此我们将初始有限元模型和基准状态下的实测模态代入式(17)求得v*，然后由式(22)对初始有限元模型进行全局修正。有限元模型修正参数及修正效果见表5。表中可见，修正后的有限元模型各阶振型与实测振型的相似度(即MAC值)相比修正前均有所提高、第二阶频率误差减小，但第三阶和第四阶的频率误差修正后反而略有增大。这主要是因为修正前，第三阶和第四阶的频率误差已经很小(小于0.5%)，而全局修正是对结构模型的全局优化，因而使其误差反而略有增大。

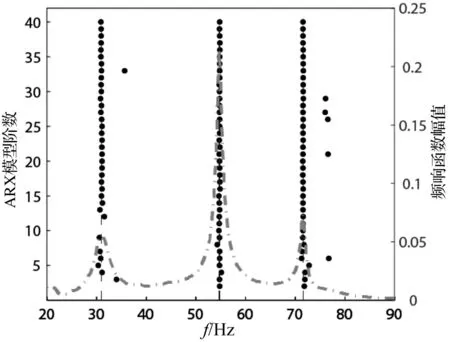
图6　结构基准状态下模态识别稳态图 Fig.6 Stability diagram under baseline condition

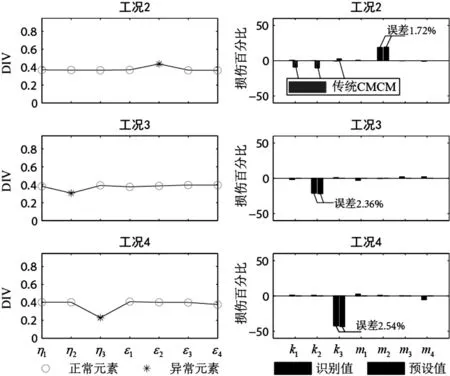
图7　损伤识别结果(LANL) Fig.7 The results of damage identification(LANL)

将表 4中各损伤状态下的实测频率与基准状态下的实测频率相对比，可以发现损伤后结构各阶频率均有不同程度的下降。将损伤状态下的实测模态和修正后的有限元模型代入式(17)求得DIV，进而对损伤进行定位和定量，识别结果如图 7所示。图中可见，各损伤工况下损伤指示向量中的异常元素均正确指示出损伤位置，损伤程度的估计也与表3中给出的预设损伤值很好地吻合(两者间的误差不超过5%)。我们还对工况2利用第1节中的传统CMCM法进行了计算， 假设结构各单元质量不发生变化，结果得出第一、二层的层间刚度大约下降10%，第三层层间刚度略有增大的错误结论。改进的CMCM局部损伤识别法中则无须人为主观地给出约束，避免了错误或者不准确的约束给损伤识别结果带来的误差。

表4　不同工况下实测模态

表5　基准状态下有限元模型全局修正

5结论

交叉模型交叉模态法是一种很好的模型修正方法，具有诸多优点，然而由于其方法中核心矩阵的缺秩，使得全局修正时必须人为添加约束。本文对传统CMCM法进行了改进，提出了以下的改进方法：首先，由基准状态下的有限元模型和损伤后实测的结构低阶模态信息求得核心矩阵，将核心矩阵最小奇异值对应的右奇异向量作为损伤指示向量(DIV)；然后，基于损伤的局部性利用聚类分析算法自动识别DIV中的异常元素，将异常元素作为损伤定位的依据；最后，由DIV估计各单元质量和刚度的损伤程度。改进后方法的优势在于：无需人为主观地添加约束即可一次性求出结构各单元质量和刚度损伤前后的变化，避免了错误或不准确的假设给损伤识别结果带来的误差。数值实验和美国LANL实验室实验均证实该改进方法切实可行，可以对损伤进行正确的定位并对损伤程度进行准确的估计(误差不超过5%)。数值实验还表明该改进方法可以在实测振型含1%的比例噪声下对损伤程度大于10%的多损伤工况进行准确的损伤定位。关于如何进一步提高改进方法的鲁棒性和对小损伤的敏感性，还有待进一步的研究工作。

参考文献

[1]李宏男，李东升. 土木工程结构安全性评估、健康监测及诊断述评[J]. 地震工程与工程振动，2002，22 (3): 82-90.

LI Hong-nan, LI Dong-sheng. Safety assessment, health monitoring and damage diagnosis for structures in civil engineering[J]. Earthquake Engineering and Engineering Vibration, 2002,22(3):82-90.

[2]宗周红, 任伟新, 阮毅. 土木工程结构损伤诊断研究进展[J]. 土木工程学报, 2003, 36(5): 105-110.

ZONG Zhou-hong, REN Wei-xin, RUAN Yi. Recent advances in research on damage diagnosis for civil engineering structures[J]. China Civil Engineering Journal, 2003, 36(5):105-110.

[3]Mottershead J E, Friswell M I. Model updating in structural dynamics: a survey[J]. Journal of Sound and Vibration, 1993, 167 (2): 347-375.

[4]李辉, 丁桦. 结构动力模型修正方法研究进展[J]. 力学进展, 2005,35(2): 170-180.

LI Hui, DING Hua. Progress in model updating for structural dynamics[J]. Advances in Mechanics, 2005, 35(2): 170-180.

[5]Friswell M, Mottershead J E. Finite element model updating in structural dynamics[M]. Springer, 1995.

[6]Doebling S W. Minimum-rank optimal update of elemental stiffness parameters for structural damage identification[J]. AIAA journal, 1996, 34 (12): 2615-2621.

[7]Kaouk M, Zimmerman D C, Simmermacher T W. Assessment of damage affecting all structural properties using experimental modal parameters[J]. Journal of Vibration and Acoustics, 2000, 122 (4): 456-463.

[8]侯吉林. 约束子结构模型修正方法[D]. 哈尔滨:哈尔滨工业大学, 2010.

[9]Hu S L J, Li H, Wang S Q. Cross-model cross-mode method for model updating[J]. Mechanical Systems and Signal Processing, 2007, 21 (4): 1690-1703.

[10]贾辉，李东升. 基于交叉模型交叉模态法的损伤识别研究[J]. 土木工程与管理学报，2011，28 (3): 133-137.

JIA Hui, LI Dong-sheng. Damage identification inversitigation based on cross-model cross-mode method[J]. Journal of Civil Engineering and Management, 2011, 28(3):133-137.

[11]王俊荣. 海洋平台结构物损伤检测与模型修正方法研究[D]. 青岛：中国海洋大学, 2009.

[12]王俊荣, 张敏, 李华军. 一种基于不完备模态信息的有限元模型修正方法[J]. 工程力学, 2010, 27 (8): 60-65.

WANG Jun-long, ZHANG Min, LI Hua-jun. A finite element model updating approach based on incomplete modal data[J]. Engineering Mechanics, 2010, 27(8): 60-65.

[13]HE Zeng-you, XU Xiao-fei, DENG Sheng-chun. Discovering cluster-based local outliers[J]. Pattern Recognition Letters, 2003, 24 (9-10): 1641-50.

[14]Figueiredo E, Flynn E. Three-story building structure to detect nonlinear effects.http://institute.lanl.gov/ei/damage_id/data/4DOF_Mat_Format.zip. 2009.

[15]Figueiredo E, Park G, Figueiras J, et al. Structural health monitoring algorithm comparisons using standard data sets[R]. LA-14393, Los Alamos, NM (United States): Los Alamos National Laboratory, 2009.

[16]Figueiredo E, Todd M D, Farrar C R, et al. Autoregressive modeling with state-space embedding vectors for damage detection under operational variability[J]. International Journal of Engineering Science, 2010, 48 (10): 822-34.

[17]Miguel R, Hernandez-Garcia, Masri S F, et al. An experimental investigation of change detection in uncertain chain-like systems[J]. Journal of Sound and Vibration, 2010, 329 (12): 2395-2409.

[18]Juang J N. Applied system identification[M]. New Jersey: PTR Prentice Hall Englewood Cliffs Inc, 1994. 175-228.

[19]沃德·海伦，斯蒂芬·拉门兹，波尔·萨斯. 模态分析理论与实验(白化同，郭继忠译)[M]. 北京：北京理工大学出版社，2001.