基于子频带谱峭度平均的快速谱峭度图算法改进

第一作者代士超男，硕士，1989年生

通信作者郭瑜男，博士,教授，博士生导师，1971年12月生

基于子频带谱峭度平均的快速谱峭度图算法改进

代士超，郭瑜，伍星，那靖

(昆明理工大学机电工程学院，昆明650500)

摘要：快速谱峭度图(Fast Kurtogram)算法具有能自适应选取共振解调频带并实现包络解调提取的优点，在滚动轴承包络分析中有广阔的应用前景，但其在实际应用中，若被采集信号中包含有较高峰值的脉冲干扰时，将可能导致谱峭度图的自适应共振带确定失效，最终导致无法获得包含有效滚动轴承的故障特征信息的包络信号。为解决快速谱峭度图算法的上述不稳定问题，本文提出了一种基于子频带谱峭度平均的改进快速谱峭度图算法，其可有效消除或削弱脉冲干扰成分对谱峭度图结果的影响，提高了共振解调频带确定的鲁棒性，实现了基于快速谱峭度图算法的滚动轴承故障特征准确提取。仿真和试验结果验证了本方法的有效性。

关键词：谱峭度，快速谱峭度图算法，包络分析，谱峭度平均

基金项目：国家自然科学基金资助项目(51365023)

收稿日期：2013-12-19

中图分类号:TH133.33

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.016

Abstract:The fast kurtogram algorithm has the advantages of choosing resonance demodulation frequency band adaptively and being able to realize the envelope demodulation extraction, so, it has broad application prospect in the rolling bearing envelope analysis. But in the fast kurtogram calculation, the existense of a high peak pulse interference in the vibration signal may result in that, the fast kurtogram calculation fails to determine the adaptive resonance frequency band, eventually the envelope may not be effectively extracted and used as the rolling bearing fault characteristic information. In order to solve the instability problem of fast kurtogram algorithm, an improvement fast kurtogram algorithm based on the average of sub-band spectral kurtosis was presented. The method can effectively eliminate or weaken the influence of pulse interference on the result of fast kurtogram, improve the robustness of the algorithm and make better the stability of the frequency band selection for resonant demodulation. The method proposed can extract the rolling bearing fault feature accurately. The simulation and experimental results veried its effectiveness.

Improvement on fast kurtogram algorithm based on sub-frequency-band spectral kurtosis average

DAIShi-chao,GUOYu,WUXing,NAJing(Faculty of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming 650500, China)

Key words:spectral kurtosis; fast kurtogram; envelope analysis; spectral kurtosis on average

包络分析(又称为共振解调分析)是目前被广泛应用的滚动轴承初期故障特征提取技术之一。包络分析的关键在于确定合适的共振解调频带参数(滤波中心频率和带宽)。近来提出的基于谱峭度的包络分析方法[1]，能够根据谱峭度值自适应地获取优化的滤波中心频率和带宽，并实现对故障特征的有效提取，其已被证明是一个非常有效的滚动轴承故障包络分析方法[2]。但研究[3]表明，当拾取信号中包含有较高峰值的脉冲干扰时，常规的快速谱峭度图算法(Fast Kurtogram)[4]将可能无法确定合理的共振解调频带[3]，进而无法有效获得滚动轴承故障信息。文献[3]中提出了一种无该问题的Protrugram算法，但该算法存在需要预先确定共振频带大概宽度的不足。本文在常规快速谱峭度图算法的基础之上，提出了一种基于子频带谱峭度平均的改进快速谱峭度图算法，其可有效消除或削弱脉冲干扰成分对原谱峭度图结果的影响，可实现存在较高峰值脉冲干扰的条件下滚动轴承故障振动共振解调优化频带的准确确定，进而实现故障特征的有效提取。仿真和试验结果验证了本方法的有效性。

1基于Fast Kurtogram的复包络提取简介

1.1谱峭度介绍

峭度(Kurtosis)对冲击信号敏感，用于描述振动信号中冲击的强弱，但易受噪声干扰而难以表征冲击的特征。近来提出的谱峭度 (Spectral Kurtosis，SK)，可反映信号峭度值随频率的变化。计算公式为[1,5]:

(1)

1.2Fast Kurtogram算法简介

Fast Kurtogram 算法的主要思想为通过构建一系列具有不同频带的1/3-二叉树带通滤波器组实现各子(频)带的谱峭度计算，并通过对子带谱峭度值的比较确定优化解调频带，进而实现解调频带对应的包络的提取[4]。其主要实现步骤包括：

(1)滤波器的构建及复包络的提取。与小波包分解算法相似，首先构建两个准解析滤波器，分别为低通滤波器h0(j)和高通滤波器h1(j)：

(2)

式中:h(j)为截止频率fc=1/8+，≥0的低通滤波器(此处频率归一化，即fs=1，一般fc取0.3)；h0(j)是由h(j)频移1/8后得到的准解析低通滤波器，其带宽为[0,1/4]；h1(j)是由h(j)频移3/8后得到的准解析高通滤波器，其带宽为[1/4,1/2]。利用以上两个滤波器分别对振动信号进行滤波，并采用2倍降采样方法进行迭代，将原信号进行L级分解，每级滤波后信号的个数为2l,把原信号分解成不同子频带下的复包络信号[4]cli(n)，其中分解级数l=0,1,…,L-1，子频带信号位置系数i=0,1,…,2l-1。分解算法可用以下公式实现：

(3)

式中:*为卷积运算。当l=0时，c0(n)≡x(n)。cli(n)可认为是原始振动信号x(t)经不同滤波器滤波后得到的子频带信号，滤波器的中心频率和带宽分别为fi=(i+1)×2-l-1和fl=2-l-1。根据包络检波原理，(n) 为第l级第i个子频带信号，是信号的包络信号。为了提高分析的精度，对频带进一步细分，在l+1和l+2级之间插入32l个滤波器，构建三个频带分别为[0,1/6]、[1/6,1/3]和[1/3,1/2]的准解析带通滤波器gj(n)(j=0,1,2)，对每个子频带信号进行再分解[4]。

(4)

(3)优化包络参数及复包络的获取。当式(4)中谱峭度K值最大时，对应于优化的中心频率fo、带宽Δfo及复包络信号c0(n)。即：

(fo,Δfo,co(n))=argmax{K(fi,Δfl)}

(5)

式中：argmax表示取最大值所对应的参数，即获得谱峭度值为最大时对应的优化中心频率和带宽，以及对应的优化复包络信号。

2Fast Kurtogram算法改进

2.1传统快速谱峭度图算法的不足

谱峭度对冲击敏感，其能表明振动信号中一系列瞬态的存在并指出它们在频域中的位置[7]。因此，利用滚动轴承局部故障对应振动信号的冲击性特征，由Fast Kurtogram算法可以自适应地确定优化的滚动轴承故障引起冲击的共振解调频带。但应注意轴承早期故障对应的振动信号通常为弱信号，易受其他高峰值脉冲成分的干扰。文献[3]指出，当采集的滚动轴承振动信号中包含高峰值脉冲干扰时，其会导致某些频带的峭度值变大，影响滚动轴承故障振动所对应共振解调频带的优化选择，进而导致包络解调失效。因此，直接用原Fast Kurtogram算法确定优化解调频带并不稳定，易受冲击噪声影响而导致后续的包络分析失败，本文后面的实验分析中也将验证这一点。

2.2基于子频带谱峭度平均的Fast Kurtogram算法

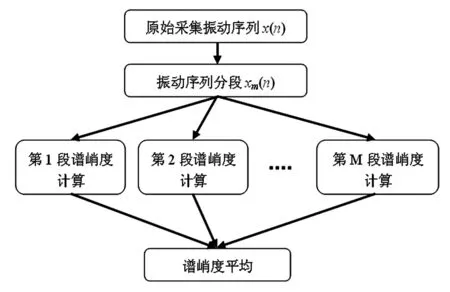
图1　基于子频带谱峭度平均的快速谱峭度图算法流程 Fig.1 Process of fast kurtogram based on the average of sub-band spectral kurtosis

众所周知，频域平均是常用的提高信噪比的有效手段，其可有效地去除频谱中非周期的随机干扰[8]。其在研究中提示我们可以将平均的概念引入到谱峭度图中作为降噪手段。为了解决上述脉冲干扰问题，在原Fast Kurtogram算法的基础之上，本文提出了基于子频带谱峭度平均的Fast Kurtogram算法。其算法流程如图1，主要步骤见图1。

(1)原始采集信号分段

将原始采集振动序列x(n)分为等长度的M段，得到分段信号xm(n)，(m=1,2,3,4,…M)。

图2　第m段数据经树状滤波器组滤波后 各级子频带峭度值 Fig.2 Kurtosis values by the tree filter group for the mth data section

(2)各段信号谱峭度计算

(3)子频带谱峭度平均

将步骤(2)中得到的m组谱峭度值数组进行对应位置求和取平均。可表示为：

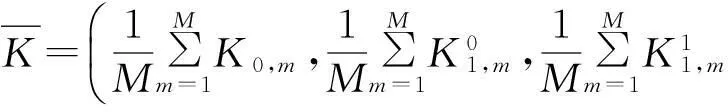
(6)

3仿真试验分析

为验证本方法的有效性，进行了仿真试验，其过程如下：仿真一个系统固有频率fr=4 000 Hz幅值为0.1的单一微弱冲击衰减的振动作为轴承故障每转内的一次冲击：

(7)

轴承故障频率为124 Hz。

仿真由三个强低频正弦干扰组成的低频干扰信号y(t)，频率分别为445 Hz、35 Hz和11 Hz，对应的幅值分别为0.3、1.0和0.8。

仿照文献[3]，仿真一固有频率f=6 000 Hz的振荡衰减脉冲p(t)作为脉冲干扰成分：

p(t)=0.75e(-Dt)cos(2πfgt)

(8)

式中：D表示震荡衰减系数。

最后仿真一个幅值为0.05的高斯白噪声干扰n(t)。最终得到仿真的轴承振动信号为：

x(t)=R(t)+y(t)+p(t)+n(t)

(9)

式中：R(t)表示为仿真的轴承衰减冲击振动信号。仿真过程中取采样频率fs=25 kHz，采样时间为10 s，仿真的滚动轴承振动信号及其各分量(图中显示时间为6.7 s~6.77 s)如图3、图4，从图中可以发现，脉冲干扰成分在整个信号中比较明显。对仿真的10 s轴承故障振动信号进行分析，截取1秒时长的信号段进行计算，有脉冲干扰存在的数据段经Fast Kurtogram计算得到滤波中心频率和带宽会失效，如图5所示。

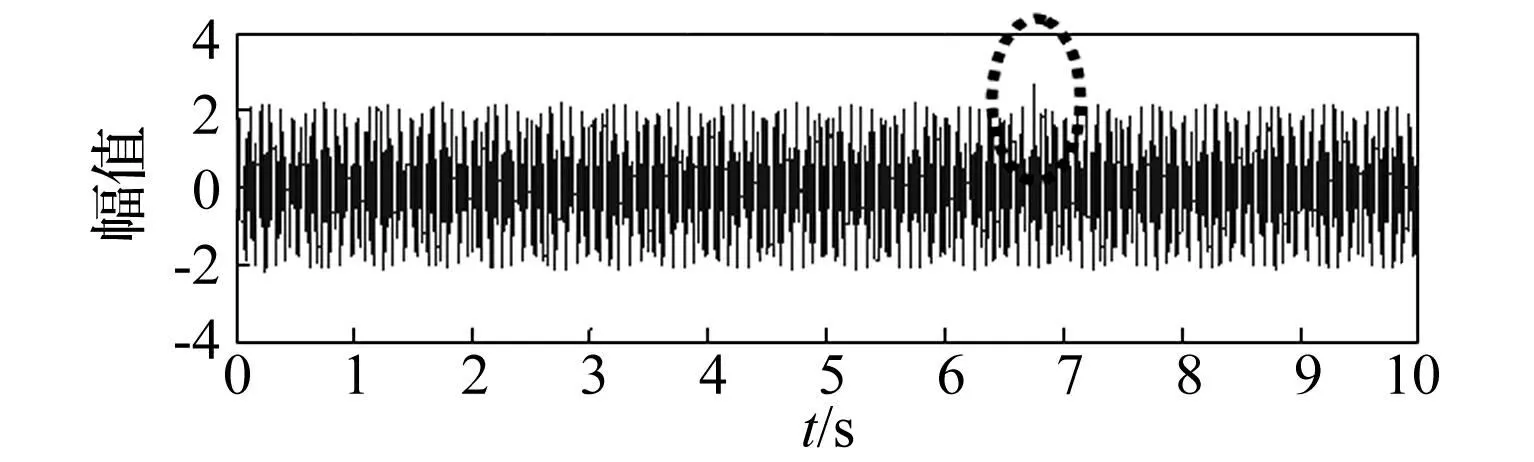
图3　仿真轴承时域信号(虚线圈内为干扰) Fig.3 Time domain simulation of bearing signal (interference in the dotted circles)

图4　仿真轴承信号组成分量 Fig.4 Simulation of bearing signal components

图5　脉冲干扰时段数据计算得到的谱峭度图 Fig.5 Kurtogram of the signal with an impulsive interference

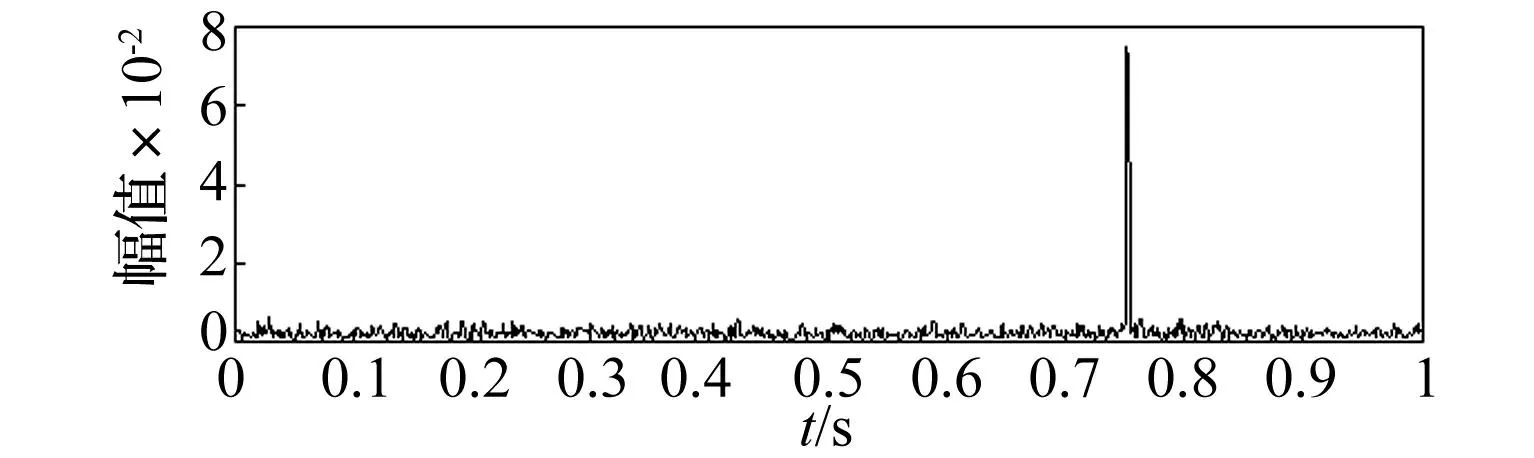
图6　仿真信号有干扰成分平方包络 Fig.6 Square envelope of simulation signal with an impulsive interference

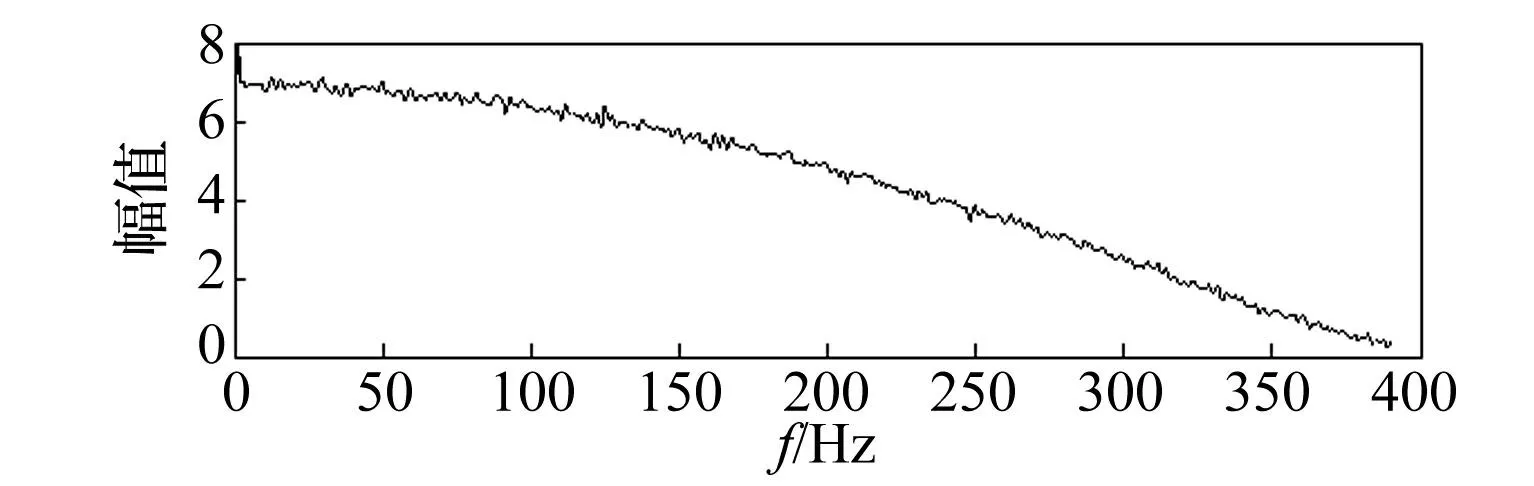
图7　仿真信号包含冲击干扰时的平方包络谱 Fig.7 Squared envelope spectrum of the simulation signal with an impulsive interference component

从图5可以看出谱峭度计算得到的滤波中心频率和带宽分别为fc=6 054.687 5 Hz、B=390.625 Hz，显然中心频率与脉冲干扰的固有频率6 000 Hz相吻合，用该参数提取平方包络[9]的时间波形如图6所示，脉冲干扰十分明显，对该包络曲线进行FFT运算，得到的平方包络谱如图7所示，不难看出无法获得轴承的故障特征频率谱线，包络分析失效。按论文中介绍的改进方法进行谱峭度平均计算，按照2.2节中所述，将10 s信号平均分为10段，分别计算谱峭度后再进行子频带谱峭度平均计算，如图8所示，得到的包络中心频率fc=3 906.25 Hz、带宽B=1 562.5 Hz，与轴承仿真数据4 000 Hz的固有频率基本吻合，用该参数进行平方包络提取获得的时间波形如图9所示，对应的平方包络谱如图10所示，与原Fast Kurtogram算法相比，采用本文所提方法计算得到的包络参数更为合理和准确。仿真结果表明本方法的可行性和有效性。

图8　子频带平均后得到的谱峭度图 Fig.8 Kurtogram after sub-frequency-band average

图9　仿真信号谱峭度平均后得到的平方包络 Fig.9 Square envelope of simulation signal after spectral kurtosis average

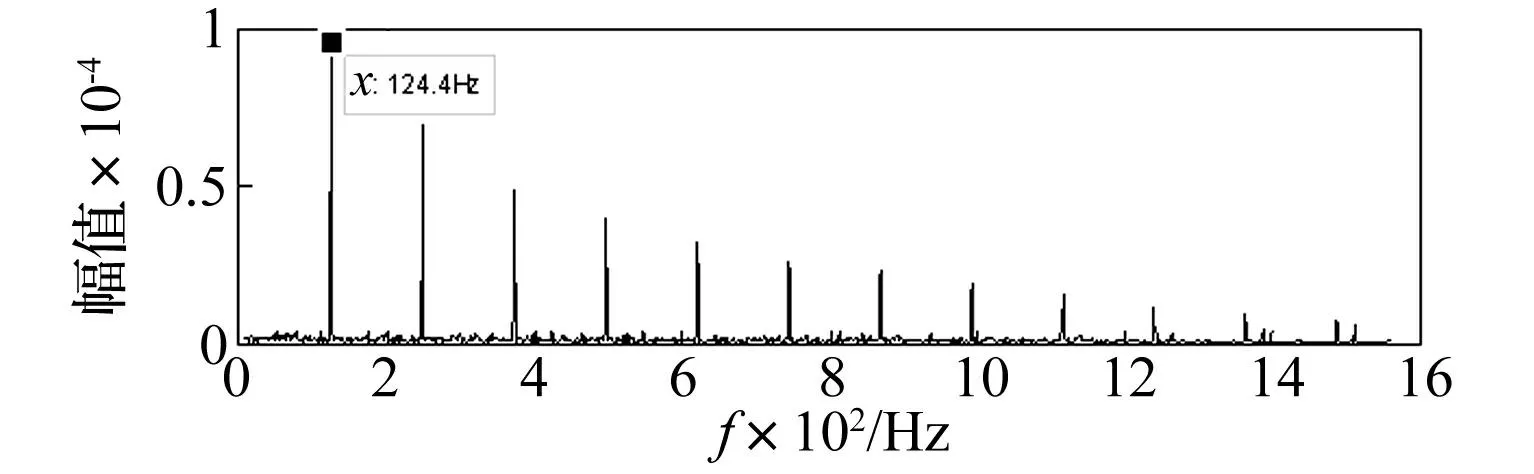
图10　仿真信号谱峭度平均后包络谱 Fig.10 FFT of simulation signal after spectral kurtosis average

4测试试验分析

测试研究中以QPZZ-Ⅱ旋转机械振动分析及故障模拟实验系统为测试对象，如图11。

图11　QPZZ-Ⅱ旋转机械振动分析及故障模拟实验系统 Fig.11 QPZZ-Ⅱ rotating machinery vibration analysis and fault simulation system

在故障轴承座内安装有一故障滚动轴承，进行滚动轴承故障实验，以外圈故障为例，试验参数如下：故障轴承的型号为NU205EM；安装轴为恒定转速1 200 r/min(对应转频为20 Hz)；数据采集设备为NI PXI-1042Q动态信号采集系统；采样频率为20 kHz；采样时间为10 s；加速度传感器为PCB加速度传感器PCB603C01；安装位置为轴承座垂直位置和两侧水平位置；转速脉冲测量传感器为电涡流位移传感器，型号为4842。图12为采集的原始振动信号时间波形，在数据段中存在某一未知源的脉冲干扰。

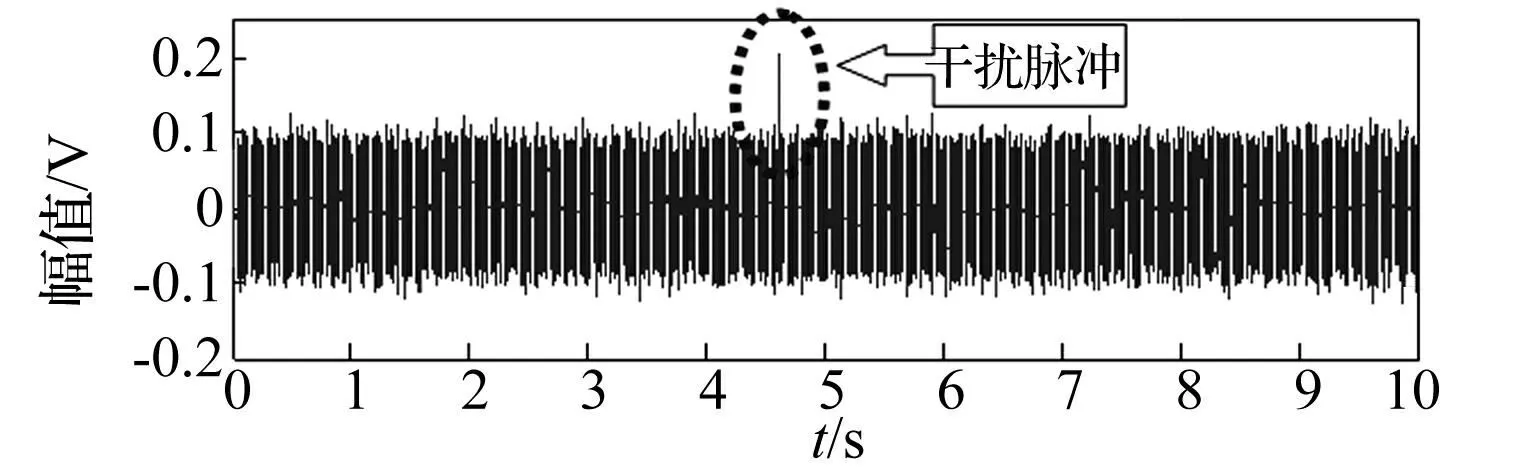
图12　原始测试振动信号 Fig.12 Original testing vibration signa

将数据信号平均分10段(分段可根据分析需要或数据长度而定)，分别对每一段数据进行Fast Kurtogram计算，获取自适应滤波中心频率和带宽。含有未知源脉冲干扰成分段(如图13)计算结果如图14所示，得到的滤波中心频率和带宽分别为fc=3 281.25 Hz、B=312.5 Hz。用该参数进行平方包络提取，其包络后时间信号如图15所示，脉冲干扰十分明显，对该包络进行FFT运算，如图16所示，谱线很杂乱，很难获得轴承的故障特征频率谱线，难以做出准确的故障诊断。

图13　有干扰成分的原始信号段 Fig.13 Original signal with an impulsive interference

图14　存在干扰成分信号段的谱峭度图 Fig.14 Kurtogram of signal with an impulsive interference

图15　有干扰成分谱峭度计算后的平方包络 Fig.15 Squared envelope of signal with an interference

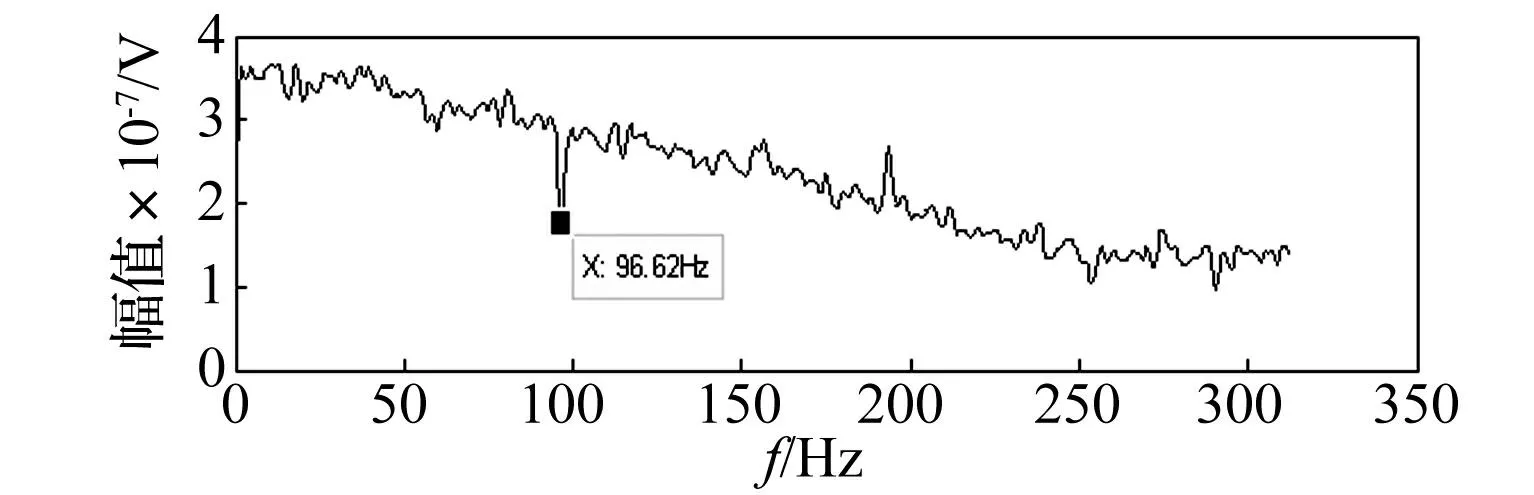
图16　原方法在有冲击干扰成分下得到的平方包络谱 Fig.16 Squared envelope spectrum by original method for signal with an impulsive interference

采用本文所提出子频带谱峭度平均的方法，将10段信号的谱峭度值进行平均计算，得到的优化滤波中心频率和带宽分别为fc=4 375 Hz、B=1 250 Hz，如图17所示。用该参数对原始轴承振动信号进行平方包络提取，其时间波形如图18所示。

图17　子频带平均后得到的谱峭度图 Fig.17 Kurtogram after sub-frequency-band average

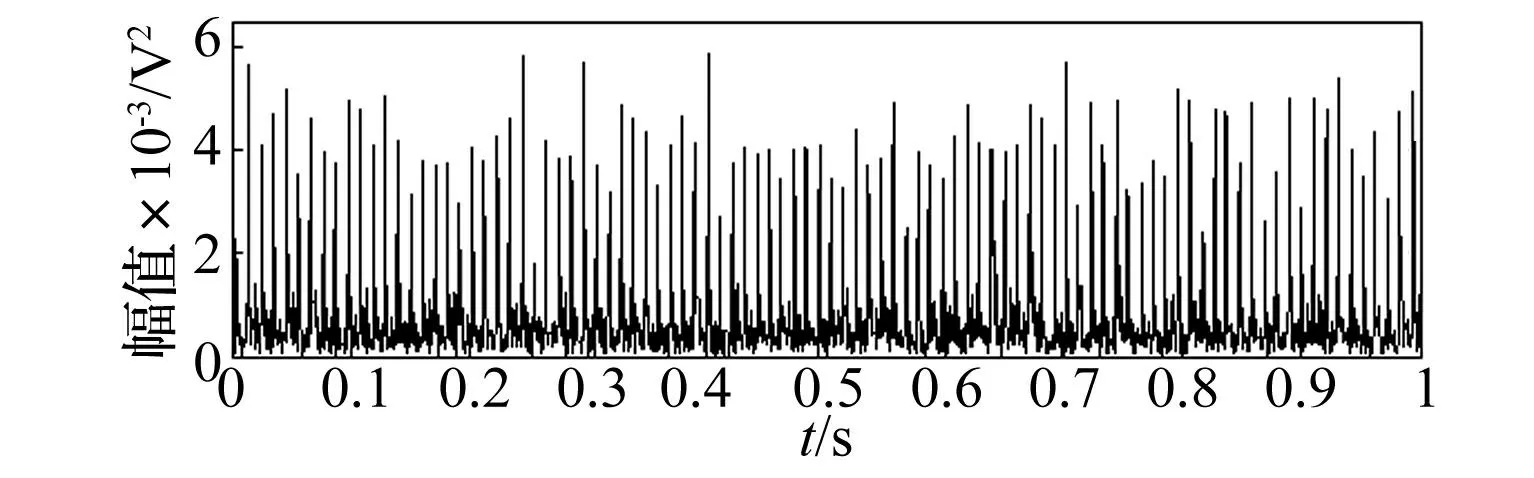
图18　谱峭度平均后得到的平方包络 Fig.18 Squared envelope after spectral kurtosis average

从图18和图15包络曲线的对比可以看出，采用子频带谱峭度平均的方法得到的参数在进行平方包络时可有效削弱脉冲干扰造成的包络不理想情况。

对该包络进行FFT运算，结果如图19所示。对比原Fast Kurtogram算法结果，采用本文所提出的方法可以在存在脉冲干扰情况下准确获得滚动轴承的故障特征频率成分及其倍频。

图19　谱峭度平均后得到的平方包络谱 Fig.19 Squared envelope spectrum after spectral kurtosis average

5结论

本文提出的基于子频带谱峭度平均的改进快速谱峭度图算法，可有效消除或削弱高峰值干扰成分对谱峭度计算的影响，避免信号中脉冲干扰导致滚动轴承优化解调频带确定的失效，提高了包络分析中滤波中心频率和带宽选择的准确性，可实现对滚动轴承故障特征的准确提取。相比文献[3]中提出的方法而言，本文所提出的方法不需要确定故障频率带宽，可直接对故障频率未知的含有高峰值干扰成分振动信号进行有效的故障特征提取和包络分析。仿真和试验结果验证了本方法的有效性。

参考文献

[1]Sawalhi N，Randall R B，Endo H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis [J]. Mechanical Systems and Signal Processing, 2007,21：2616-2633.

[2]Antoni J，Randall R B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines [J]. Mechanical Systems and Signal Processing, 2006,20(2)：308-331.

[4]Antoni J. Fast computation of the kurtogram for the detection of transient faults [J]. Mechanical Systems and Signal Processing, 2007,21(1)：108-124.

[5]郭瑜，郑华文，高艳，等. 基于谱峭度的滚动轴承包络分析研究 [J]. 振动.测试与诊断, 2011,31(4)：517-521.

GUO Yu，ZHENG Hua-wen，GAO Yan，et al. Envelope analysis of rolling bearings based on spectral kurtosis [J]. Journal of Vibration，Measurement & Diagnosis，2011，31(4)：517-521.

[6]刘亭伟，郭瑜，李斌，等. 基于谱峭度的滚动轴承故障包络阶比跟踪分析 [J]. 振动与冲击，2012,31(17)：149-153.

LIU Ting-wei，GUO Yu，LI Bin，et al. Envelope order tracking analysis for rolling element bearing faults based on spectral kurtosis [J]. Journal of Vibration and Shock，2012，31(17)：149-153.

[7]Antoni J. The spectral kurtosis: a useful tool for characterising non-stationary signals[J]. Mechanical Systems and Signal Processing, 2006，20(2)：282-307.

[8]鞠萍华，秦树人，秦毅，等. 多分辨 EMD 方法与频域平均在齿轮早期故障诊断中的研究 [J]. 振动与冲击, 2009，28(5)：97-101.

JU Ping-hua，QIN Shu-ren，QIN yi，et al. Research on gear earlier fault diagnosis by method of multi-resolution empirical mode decomposition and frequency domain averaging[J]. Journal of Vibration and Shock，2009，28(5)：97-101.

[9]Ho D，Randall R B. Optimisation of bearing diagnostic techniques using simulated and actual bearing fault signals [J]. Mechanical Systems and Signal Processing，2000，14(5)：763-788.