覆冰导线动态气动力特性模拟与分析

第一作者张喆女，硕士生，1988年生

通信作者杨秀萍女，教授，硕士生导师，1962年生

覆冰导线动态气动力特性模拟与分析

张喆1,2，杨秀萍1,2，郝淑英2

(1.天津理工大学 天津市先进机电系统设计与智能控制重点实验室，天津300384; 2.天津理工大学机械工程学院，天津300384)

摘要：为研究覆冰导线舞动时气动力的特性，从弱耦合角度出发，基于流体动力学仿真软件Fluent二次开发，利用用户自定义函数对导线的舞动轨迹进行编程并结合动网格技术实现流固耦合。计算了新月形覆冰导线在横向振动下的气动力系数，并与静态模拟结果和试验结果进行比较；分析了舞动幅值、频率和扭转振动对动态气动力的影响。结果表明：相同风速下，动态气动力系数大于静态值，二者具有相同的变化规律；阻力、升力系数随舞动幅值增大显著增加，特别是升力系数成倍增加；振动频率增加，也使动态气动力系数增大，但频率对动态气动力的影响小于幅值的影响；扭转振动对动态气动力有一定的影响。工程中采用静态气动力系数预测大档距舞动引起的断线的临界风速和塔承受的荷载，其结果不安全，应考虑动态气动力系数对舞动的影响。

关键词：覆冰导线；动态气动力系数；舞动；数值模拟

基金项目：天津市自然科学基金项目(11JCYBJC05800)

收稿日期：2013-08-08修改稿收到日期：2014-02-22

中图分类号:O355；TM726

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.033

Abstract:In order to study the aerodynamic characteristics of galloping of iced conductor, based on software Fluent redevelopment, a user-defined function was introduced to describe the track of conductor galloping and the dynamic mesh technology was used to realize the fluid and solid coupling in accordance with a weakly coupled model. The aerodynamic coefficients of crescent iced conductor during lateral vibration were calculated, and compared with the results from simulation of the conductor in static state and also from experimental data. The effects of galloping amplitude, frequency and torsional vibration on the dynamic aerodynamic forces were analyzed. The results show that the dynamic aerodynamic coefficients are larger than the static ones, and they have the same variation trend under the same wind speed. Drag and lift coefficients increase significantly with the increase of galloping amplitude, especially the lift coefficient will be multiplied. The frequency increase also makes the dynamic aerodynamic coefficients increasing, but the effect of frequency on the dynamic aerodynamic force is less than that of amplitude. Torsional vibration has a certain influence on the dynamic aerodynamic force. When the static aerodynamic coefficients are used to forecast the critical wind speed of conductor break and the tower loads caused by large span galloping in engineering, the results tend to be unsafe. The effects of dynamic aerodynamic coefficients on galloping should not be ignored.

Numerical simulation and analysis of dynamic aerodynamic characteristics of iced conductor

ZHANGZhe1,2,YANGXiu-ping1,2，HAOShu-ying2(1. Tianjin Key Laboratory of the Design and Intelligent Control of the Advanced Mechatronical System, Tianjin 300384, China;2. School of Mechanical Engineering, Tianjin University of Technology, Tianjin 300384, China)

Key words:iced conductor; dynamic aerodynamic coefficient; galloping; numerical simulation

非圆截面的覆冰导线在一定风速条件下易发生低频大振幅的舞动，对输电线路的安全构成严重威胁。自上世纪以来，国外学者开始了导线舞动机理的相关研究。目前国际上普遍接受的有Den Hartog[1]的横向舞动机理、Nigol[2]的扭转舞动机理和Yu[3]的惯性耦合机理等。

由上述三种舞动机理可知，气动力系数对研究覆冰导线的舞动至关重要。国内外研究舞动行为时，通常是把静态试验得到的气动力系数用于动态驰振的机理分析和舞动的数值模拟研究[4]，对其精确性进行详细研究的学者并不多。由于覆冰导线的垂直振动与扭振耦合，实际的气动力随时间和导线位置、速度等时刻变化，这种“准静态”假设并不完全适用，有必要采用动态试验或模拟的方法来考察覆冰导线的动态气动力系数，即导线在与气流相对运动过程中产生的气动力特性，考虑流固耦合的因素，以便进一步准确预测和抑制覆冰导线的舞动。

在研究动态气动力方面，Kimura等[5-6]对类似新月形覆冰导线在横向振动和扭振状态下的升力和扭转系数进行试验研究，验证了静态气动力系数在一定程度上的适用性，比较了动态气动力与静态气动力的不同。李万平等[7]对三分裂覆冰导线进行了动态气动力特性试验，讨论了准静态假设在覆冰导线群的驰振分析中的适用性。目前，对于覆冰导线的动态气动力还缺乏更多的研究。由于动态气动力系数的获得需要更为复杂的试验设备和装置，且舞动时的运动参数很难确定，特别是大档距、舞动振幅较大时。因此本文采用数值方法，从弱耦合角度出发，对流体动力学仿真软件Fluent进行二次开发，利用用户自定义函数对导线的舞动轨迹进行编程并结合动网格技术实现流固耦合，研究覆冰导线在横向振动下气动力系数的变化规律，分析舞动振幅、频率及扭转对气动力的影响。该研究可为准确分析覆冰输电线路的动力学特性和设计输电线路提供依据。

1基本方程与求解方法

流体域的控制方程可用二维不可压缩粘性流体的连续性方程和N-S方程来描述。

连续方程

(1)

动量方程

(2)

式(1)、(2)中ρ为流体密度；μ为动力粘度系数；p为流体压强；u、v分别为流体沿x方向和y方向的速度。

湍流模型采用标准k-ε模型，输运方程为

(3)

式中k和ε为两个未知量；k和ε分别为湍动能k和耗散率ε对应的Prandtl数，分别取1和1.3；C1ε、C2ε和Cμ为经验常数，分别取1.44、1.92和0.09。

覆冰导线所受空气动力载荷主要包括阻力FD，升力FL和扭矩FM，分别表示为

FD=ρU2LDCd/2

FL=ρU2LDCl/2

FM=ρU2LD2Cm/2

(4)

式中:Cd、Cl和Cm分别为阻力、升力和扭矩系数；U为风速；L为导线长度；D为导线直径。

试验和数值模拟表明，覆冰导线舞动轨迹为斜椭圆，其运动参数化方程可表示为

(5)

运动速度为

式(5)、(6)中ω为导线振动的圆频率；a为椭圆轨迹的半长轴，b为半短轴；β为椭圆长轴与y轴正方向的夹角。

导线扭转视为简谐振动，方程为

θ=Asin(ωθt)

(7)

角速度为

(8)

式(7)、(8)中A为扭转幅值，ωθ为扭转圆频率。

2静态和动态气动力系数分析

2.1计算模型

以新月形覆冰导线为研究对象，截面形状如图1，根据文献[8]风洞试验模型，选取导线直径D为33 mm，覆冰厚度H为14 mm，风速为12 m/s，分别计算了不同攻角下静态与动态气动力系数。

建立计算模型时，为了使尾流能充分发展，减小边界对流场计算的影响，静态模拟时计算域[9]取为-15D≤x≤40D，-15D≤y≤15D，坐标原点位于导线的中心，采用分块非结构化网格，总网格14万，在覆冰导线所在的中心区域局部加密，最小网格尺寸为0.5 mm，计算步长0.05 s，共计算50 s。

图1 60°攻角下新月形覆冰导线Fig.1Thecrescenticedtransmissionlineat60°attackangle图2 动态计算区域示意图Fig.2Schematicdiagramofdynamiccalculationarea

动态模拟时计算域[9]取为-55D≤x≤60D，-40D≤y≤40D，坐标原点为初始时刻的导线中心，采用非结构化网格，覆冰导线运动区域定义为动网格，该部分网格随覆冰导线截面的运动而变化，用弹簧光顺法和尺度函数修改网格形状及尺度，总网格14万左右，在覆冰导线所在的中心及动网格区域局部加密，最小网格尺寸为0.5 mm，图2为动态计算区域示意图。

静、动态模拟采用相同边界条件，入口为速度入口，出口为压力出口，上、下两侧采用对称边界条件，覆冰导线的表面为壁面。湍流模型均采用标准k-ε模型，压力速度耦合采用SIMPLE算法，对动量、湍动能以及湍动能耗散率方程均采用二阶精度离散格式。

根据式(5)、(6)利用VC++编写用户自定义函数控制导线舞动的轨迹及速度。导线舞动的振幅和频率参考文献[10]选取，档距为126 m时，对应的a=1.03 m，b=0.43 m，β=30°，频率f=0.5 Hz，按逆时针方向舞动，计算步长为0.01 s，共计算了38 s，19个周期。

2.2计算结果

图3　静、动态气动力系数比较 Fig.3 Comparison with the aerodynamic coefficients of static and dynamic

图3(a)~(c)为静态和动态气动力系数模拟结果与风洞试验结果[8]的比较图，可以看出静态气动力系数与试验值较为吻合，动、静态气动力系数具有相同的变化规律。动态阻力系数在每个攻角下均大于静态值0.2~0.3(增加14%~25%)；动态升力系数大于静态值0.1~0.2(增加35%~1倍)，动态扭转系数与静态值较接近，在曲线两个尖峰处差别较大，约为10%。

动态气动力系数随时间和位置变化，图3(d)为60°攻角时静、动态阻力系数和升力系数随时间变化曲线，由于导线舞动时扭转中心随时间变化，计算时每个舞动周期选取10个位置，随时更新扭转中心坐标，记录和读取相应的扭矩系数，然后取平均值，因此文中未给出动态扭矩系数随时间变化的曲线(以下同)。动态阻力系数和升力系数的振动频率均为0.5Hz，与导线舞动频率相同。

2.3结果分析

以攻角60°为例进行分析，图4为静态及动态导线一个周期内不同位置时网格、速度与压力云图，图5为静、动态导线周边压力系数分布图，横坐标起点A从图中导线的A点位置开始，按逆时针方向沿导线表面周向长度计算，B、C点的位置也与导线上的位置相对应。

图4　静、动态网格、速度与压力云图 Fig.4 Distributions of mesh, velocity and pressure in static and dynamic simulation

与静态时相比(图4(a)及图5中的静态曲线)，导线自下而上运动时(对应图4(b)、(e)及图5中t=3.9 s和t=4.8 s的曲线)，水平振动速度方向与来流速度方向相反，合成后使速度减小，驻点压力增加，分离点向覆冰一侧前移，背风面压力降低，致使阻力增加；垂直方向振动使顶部速度增加，负压增大，底部负压减小，使升力增大。

导线自上而下运动时(对应图4 (c)、(d) 及图5中t=4.2 s和t=4.5 s的曲线)，水平振动速度方向与来流速度方向一致，合成后使速度增大，驻点压力减小，且位置下移，底部分离点后移，但覆冰侧的分离点基本没变，背风面负压区的压力仍比静态时小，因此阻力变化不明显；垂直方向振动使底部速度增加，压力减小，由于底部形状为圆弧，底部负压区域减小，顶部负压区域增大，升力略有增加。

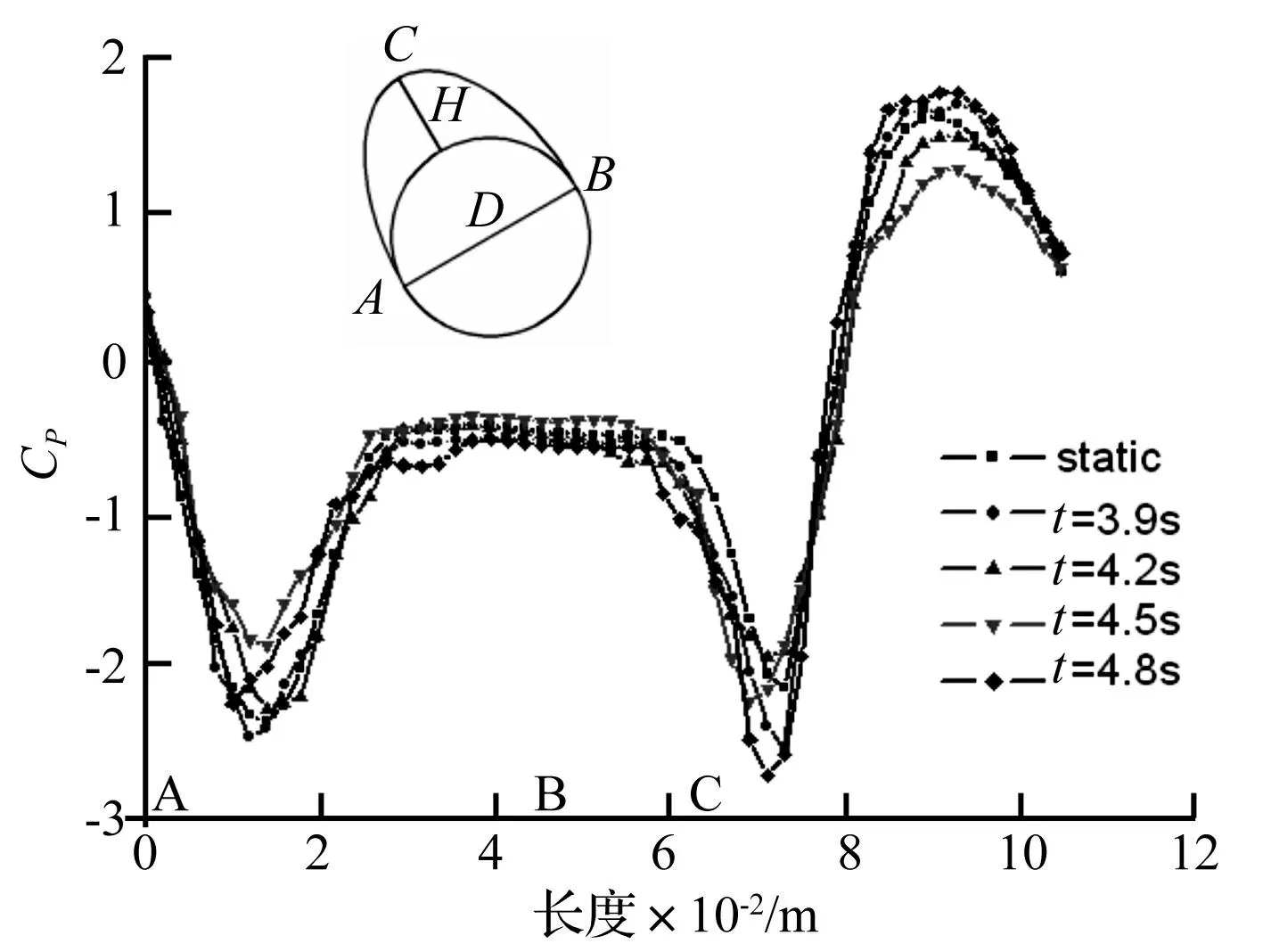
图5　静、动态压力系数分布的比较 Fig.5 Comparison with pressure coefficients distribution

3参数对动态气动力系数的影响

3.1舞动幅值及频率的影响

覆冰导线舞动是一种低频、大振幅的自激振动，其振动频率通常为0.1 Hz～3 Hz，振幅约为导线直径的5倍～300倍[11]。为研究振幅和频率对气动力的影响，模拟中选取振幅在0.06 m～2.86 m之间(对应幅值与导线直径比δ为2.2~104)，每增加0.4 m为一计算工况，舞动频率在0.2 Hz～1.2 Hz之间选7个频率工况，共计56个计算工况。定义振幅为椭圆长轴，长轴与短轴之比为2.4，长轴与y轴正方向夹角β为30°，不考虑导线扭转的影响。风速18 m/s，导线直径27.6 mm，覆冰厚度12 mm，攻角为60°。

图6给出了舞动幅值及舞动频率变化对气动力系数影响的关系曲线。可以看出：幅值增加时，阻力系数和升力系数均方值均显著增加；扭转系数则呈现波动趋势，数值在0.1~0.14之间变化。幅值较低时，频率增加对三个系数影响不明显，幅值超过1.66m(δ为60)时，阻力系数和升力系数随频率的增大而增加，扭转系数也有增加的趋势，但数值增加较前两者要小。

频率为1.2 Hz时，振幅由0.06 m增至2.86 m(δ从2.2~104)时，阻力系数增加48%，升力系数增加4.2倍，扭转系数增加22%，由此可知振幅对动态气动力系数具有显著影响。

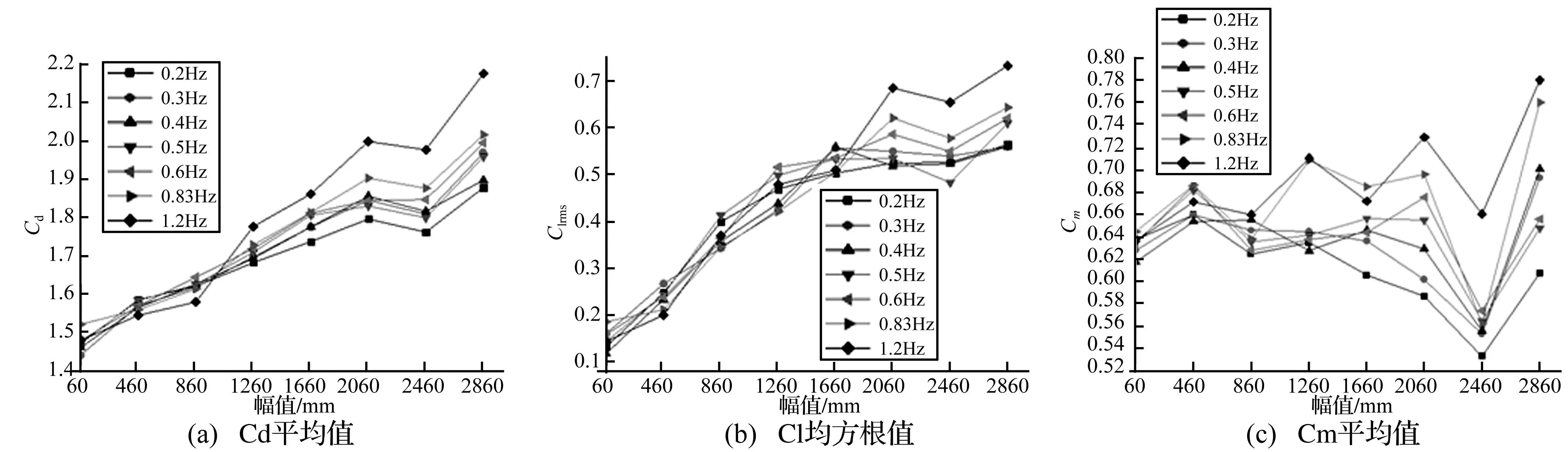
图6　舞动幅值和频率对动态气动力系数的影响 Fig.6 Galloping amplitude and frequency effects on dynamic aerodynamic coefficients

大档距导线覆冰舞动的幅值远大于小档距线路，且此时是假设两者具有相同的气动系数，由此可知大幅值舞动动态气动系数的显著增加使得大档距导线实际舞动的幅值远大于依照静态气动系数计算得到的幅值，且导线实际承受的动态张力及其作用在输电塔上的力远大于由静态计算给出的结果。同时输电线张力的增加改变了输电线的刚度，刚度的增加使得系统的瞬时固有频率增大[12]，阻力系数和升力系数随频率的增大而增加，如此也将使气动力增加。

因此采用静态气动力系数预测大档距舞动引起的断线的临界风速和塔承受的荷载，其结果不安全，应考虑动态气动力系数对舞动的影响。

3.2扭转振动的影响

在3.1节模型基础上，导线舞动时同时考虑横向振动及扭转振动，扭转振动根据公式(7)、(8)定义扭转角及角速度。由于覆冰导线实际舞动时扭转角很小[13]，选取扭转的幅值为±10°，扭转频率为0.5 Hz，导线横向振动频率也选为0.5 Hz，初始攻角为60°，振动幅值a=230 mm。

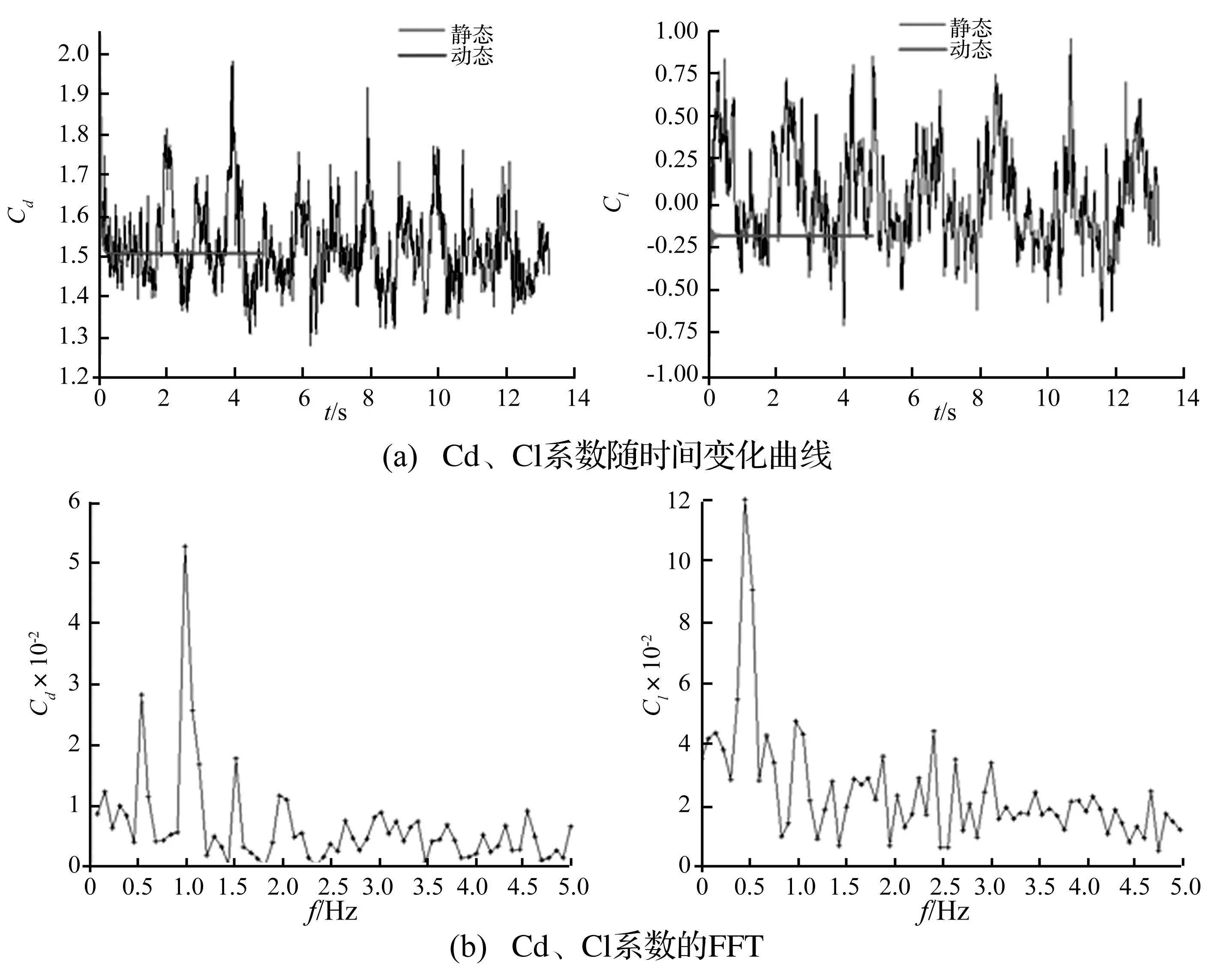
图7　考虑扭转时阻力、升力系数曲线及FFT Fig.7 The time history curves and FFT of drag and lift coefficients considering torsion

图8　静态、考虑扭转时网格、速度与压力云图 Fig.8 Distributions of mesh, velocity and pressure in static and torsion

图7为阻力和升力系数随时间变化曲线及对应的FFT图，可以看出：一个周期内攻角从60°→50°→60° →70°→60°变化，阻力系数按减小→增加→减小的趋势变化，主频率为1Hz，是横向振动及扭转振动频率的2倍，平均值为1.52，静态为1.51，二者接近；升力系数则按增加→减小→增加的趋势变化，频率为0.5Hz，与横向振动及扭转振动的频率相同，平均值近似为0，为说明脉动影响，计算出均方根值为0.24，静态值为-0.19。

图8(a)为静态网格、速度及压力云图，图8(b)~(e)为考虑横向振动和扭转振动时一个周期内4个不同位置对应的网格、速度及压力云图。导线横向振动的同时有扭转运动，其流场非常复杂，流速和压力分布随时间的变化受导线位置和攻角的共同影响，攻角相同时，静态、动态不同位置时的分布也不相同，如图8(a)、(c)和(e)，攻角均为60°。

图9为导线仅横向振动和考虑横向及扭转时的气动力系数对比图。可以看出：两种情况下，阻力系数和升力系数随舞动幅值增加而增大的变化规律相同。与仅考虑横向振动相比，考虑扭转时的阻力系数略小，数值相差小于0.05(5%)，但阻力系数的振动频率发生改变；升力系数均方值则有所增加，最大相差0.1(20%)；扭转系数呈现波动状态，数值相差小于0.05(9%)，因此在本文研究的范围内，扭转振动对动态气动力系数有一定的影响。

4结论

利用Fluent软件二次开发的UDF编程和动网格技术，对覆冰导线的动态气动力系数进行计算与参数分析，得到以下结论：

(1)新月形覆冰导线横向振动下的动态气动力系数大于静态值，二者具有相同的变化规律；

(2)相同攻角和风速下，阻力、升力系数随舞动幅值增加明显增大，特别是升力系数成倍增大；振动频率增加时，气动力系数随之增大；但频率对动态气动力的影响小于幅值的影响；

(3)扭转振动对动态气动力系数的大小有一定影响，同时使动态阻力系数的振动频率发生改变。

图9　考虑扭转时与横向舞动气动力系数对比 Fig.9 Comparison with the aerodynamic coefficients of the torsion and lateral galloping

(4)工程采用静态气动力系数预测大档距舞动引起的断线的临界风速和塔承受的荷载，其结果不安全，应考虑动态气动力系数对舞动的影响。

参考文献

[1]Den Hartog J P. Transmission line vibration due to sleet[J]. Transaction AIEE，1932, 51(4):1074-1086.

[2]Nigol O,Clarke G J. Conductor galloping and its control based on torsional mechanism[J]. Ontario Hydro Research Quarterly，1974, 26(2): 31-41.

[3]Yu P, Popplewell N,Shah A.H. Instability trends of inertially coupled galloping[J]. Journal of Sound and Vibration, 1995, 183(4)：663-678.

[4]蔡萌琦，严波，吕欣，等.覆冰四分裂导线空气动力系数数值模拟[J].振动与冲击,2013,32(5):132-137.

CAI Meng-qi, YAN Bo, LÜ Xin, et al. Numerical investigation on aerodynamic coefficients of iced quad bundle conductor[J]. Journal of Vibration and Shock, 2013,32(5):132-137.

[5]Kimura K M, Inoue Y, Fujino T, et al. Unsteady forces on an ice-accreted four-conductor bundle transmission line[C]// Proc. of the 10th Int. Conference on Wind Engineering, Copenhagen(Denmark),Wind Engineering into the 21st Century, Eds. A. Larsen, GL. Larose and F. M. Livesey, A. A. Balkema, 1999: 467-472.

[6]Shimizu M, Ishihara T, Phuc P V. A wind tunnel study on steady and unsteady aerodynamic characteristics of ice-accreted transmission lines[C]// Proc. of the 18th Symposium on Wind Engineering, Tokyo (Japan), 2004: 245-250.

[7]李万平. 覆冰导线群的动态气动力特性[J]. 空力动力学报，2000,18(4): 413-420.

LI Wan-ping. Dynamicaerodynamic characteristics of the galloping of bundled iced power transmission lines[J]. Acta Aerodynamica Sinica, 2000,18(4): 413-420.

[8]王侠. 覆冰导线空气动力特性风洞试验及数值模拟[D]. 重庆：重庆大学, 2012.

[9]孙晓颖，许伟，武岳. 钝体绕流中的计算域设置研究[C]//第十三届全国结构风工程学术会议论文集. 大连：大连理工大学出版社，2007.1036-1041.

[10]范孜. 覆冰分裂导线的动力学特性研究[D]. 天津：天津理工大学, 2012.

[11]郭应龙，李国兴，尤传永. 输电线路舞动[M]. 北京：中国电力出版社, 2003.

[12]郝淑英，冯海茂，范孜,等．覆冰输电线非线性瞬时固有频率研究[J]. 工程力学, 2013,30(9): 283-287.

HAO Shu-ying, FENG Hai-mao, FAN Zi, et al. Investigation of nonlinear transient natural frequency of iced transmission line[J]. Engineering Mechanics, 2013,30(9): 283-287.

[13]严波，胡景，周松，等.覆冰四分裂导线舞动数值模拟及参数分析[J]. 振动工程学报，2010,23(3): 310-316.

YAN Bo, HU Jing, ZHOU Song, et al. Numerical simulation and parameter analysis of galloping for iced quad-bundled conductor[J]. Journal of Vibration Engineering, 2010,23(3): 310-316.