支持向量机改进算法在船舶桨叶数分类中的应用

戴卫国，李海涛，李智忠，王易川

(海军潜艇学院，山东 青岛266042)

0 引 言

船舶辐射噪声的复杂性使得很难对其进行分类与识别，船舶辐射噪声的特征提取和分类方法是人们一直研究探索的技术难题。船舶辐射噪声(Detection of Envelope Modulation On noise，DEMON)谱反映了航行舰船噪声的节奏信息和船舶本身一些固有的物理不变特征，通过对船舶辐射噪声的DEMON 谱分析可以获取船舶目标桨叶数特征［1］;船舶目标桨叶数物理意义明确，与船舶工况无相关性，是进行水声目标识别最重要的识别特征之一，在某些情况下单凭桨叶数即可识别目标，这对舰船目标识别具有特别的意义。

支持向量机 (Support Vector Machine，SVM)是一种基于统计学习理论的模式识别方法，采用结构风险最小化原则代替了传统机器学习方法中的经验风险最小化原则，在解决有限样本、非线性及高维模式识别问题中表现出许多特有的优势，与其他学习机相比具有良好的推广能力和很强的普适性［2-3］。

本文利用船舶目标辐射噪声DEMON 谱特征，采用径向基支持向量机改进算法，实现了对船舶螺旋桨桨叶数的分类识别应用研究。针对支持向量机算法［2-3］对噪声比较敏感和最优分类面求解时约束太多不利于求解问题，根据支持向量机在不等式约束条件下可以保持支持向量解的稀疏性特性，在应用径向基等平移不变核函数的情况下，对支持向量机的松弛变量和决策函数2 方面进行改进，从而构造齐次决策二阶损失函数径向基支持向量机的分类算法(简称:径向基支持向量机改进算法)，在支持向量机算法中实现二次规划中的最小约束条件下最优分类面求解，研究其Matlab实现方法，并采用扩展的XOR 仿真数据、双螺旋仿真数据、船舶辐射辐射噪声数据进行螺旋桨桨叶数分类识别实验。实验表明，该算法具有分类面划分合理、模型参数寻优空间广阔、总体分类性能优的特性。

1 支持向量机改进算法

1.1 支持向量机原理

支持向量机从线性可分情况下的最优分类面发展而来，最优分类面是要求分类面不但能将两类正确分开，而且使分类间隔最大。d 维空间中线性判别函数的一般形式为g(x)=w·x +b，设分类面的方程为(w·x)+b = 0，使得对线性可分的样本集(xi，yi)，i = 1，2，…，l，x ∈Rd为输入样本，d 为训练样本维数，y ∈{+1，－1}为输出类别，满足yi［(w·xi)+ b］－1 ≥0，i = 1，2，…，n［1］。

在线性不可分和在非线性情况下，通过在求解二次规划约束条件中增加一个非负的松弛项ξi，以及引入核函数K(xi，xi)= φ(xi)·φ(xi)后，支持向量机的分类问题转化为求(w，b，ξ)T为决策变量的二次规划问题［4-5］:

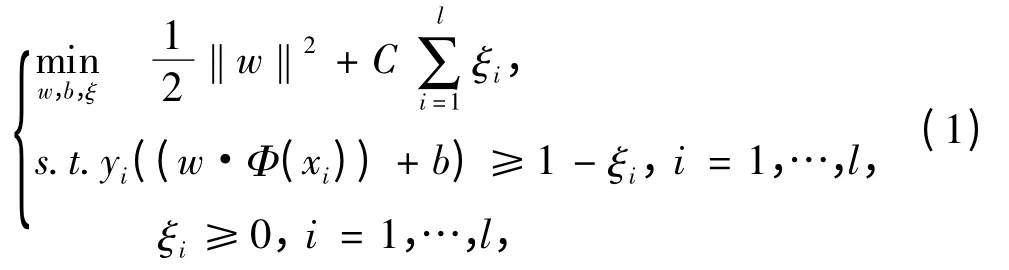
式中:C 为惩罚因子;ξ=(ξ1，…，ξl)T。

该问题可通过求解其拉格朗日对偶问题得其最优解，其对偶问题为:

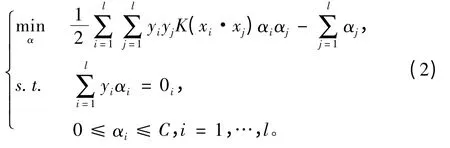
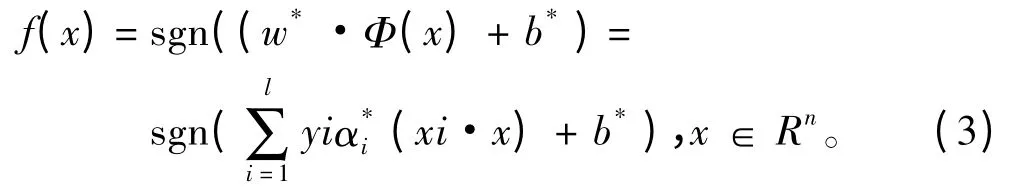
1.2 支持向量机改进算法

支持向量的稀疏性是支持向量机的主要特性之一。在保持支持向量稀疏特性的前提下，为解决支持向量机算法对噪声比较敏感的问题，并寻求最小约束中条件下的最优分类面寻优，对支持向量机在以下2 个方面进行改进:一是将松弛变量ξi采用的一阶函数形式改为二阶函数形式，即在目标函数中采用来代替此改进可以去掉所求解的二次型规划的对偶问题中关于αi不等式约束中的上限约束条件αi≤C，i = 1，…，l，并钝化支持向量机算法对噪声数据的敏感性;二是根据径向基核函数具备的平移不变性，在基于径向基核函数的支持向量机算法中，可对支持向量机决策函数进行齐次处理去掉偏置b，将其决策函数修改为f(x)= sgn(w*·Φ(x))，从而在求解二次规划问题的对偶问题时，可减少关于αi等式约束条件仅余下不等式约束中的下界约束αi≥0，i = 1，…，l。通过此2 处改进，构建了基于径向基核函数的齐次决策二阶损失函数支持向量机的改进算法，从而实现二次规划中的最小约束条件下最优分类面求解。

此时其原始问题的目标函数和约束条件为

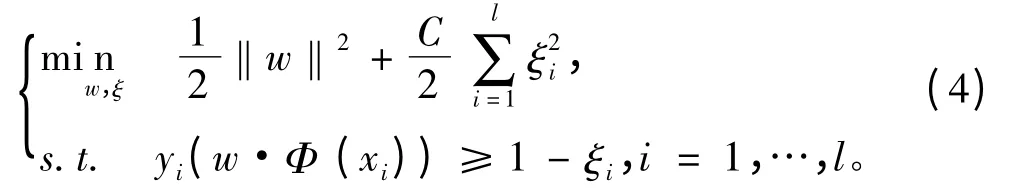
此目标函数为凸函数，不等式约束条件为线性函数，强对偶条件成立［6］。求解式(4)的对偶规划，引入拉格朗日函数

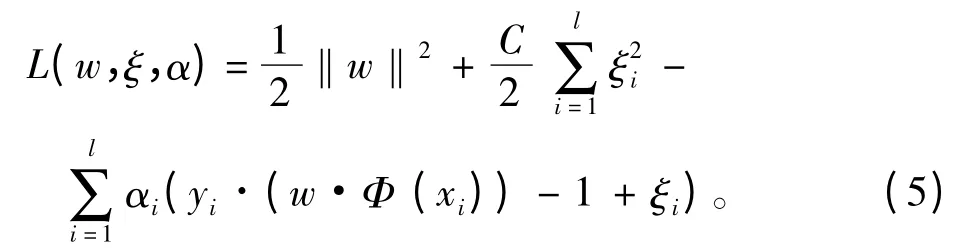
先求拉格朗日函数L(w，ξ，α)关于w，ξ 的极小值

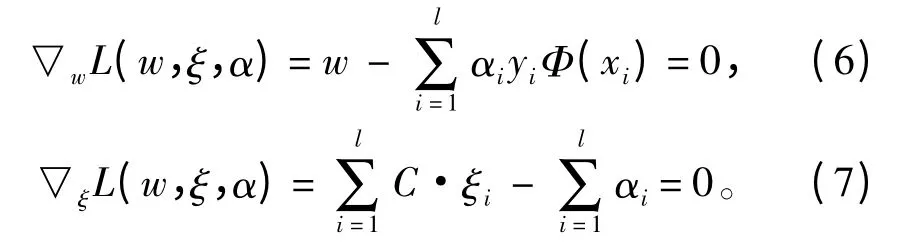
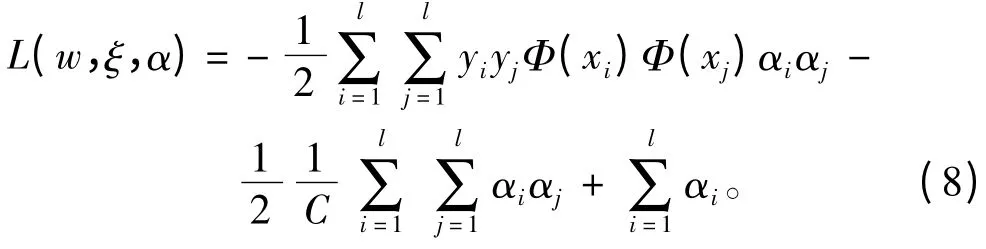
所以原始问题的对偶问题可表示为

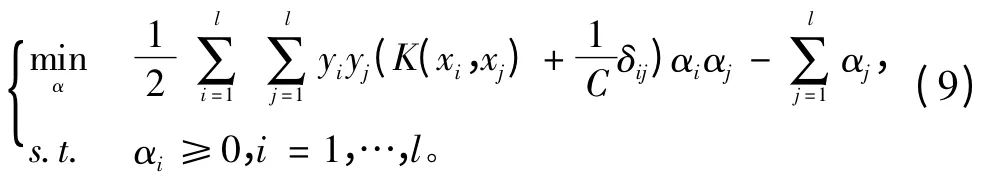
1.3 支持向量机改进算法的Matlab 实现

关于在线性约束条件下的二次规划问题，在Matlab 中专门提供了用于求解二次规划问题的quadprog 函数，可直接用于求解中等规模的支持向量机问题。相对于大规模的支持向量机求解的选块算法、分解算法、序列最小最优化算法而言，quadprog 函数直接求解方法意义明确、中间变量清楚、过程可控，且运算速度可行，是一种较好的学习及调试手段。

quadprog 函数求解的最优化问题形式为［7］:

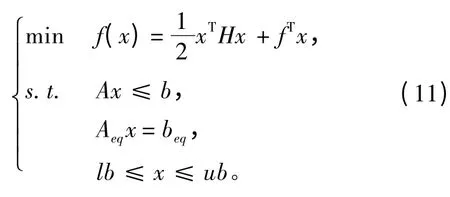
对于支持向量机和支持向量机改进算法，应用quadprog 函数求解的对比如表1 所示。

表1 应用Quadprog 函数求解支持向量机实现方法对比Tab.1 The comparation between SVM and improved algorithm on Quadprog function

2 仿真数据分类实验分析

为了验证该支持向量机改进算法的实际效果，本文利用扩展的XOR 仿真数据和双螺旋线仿真数据进行实验分析。

2.1 扩展的XOR 仿真数据分析

平面上相间排列的25 点的两类点集，可以看作是扩展的XOR 数据，如图1 所示。

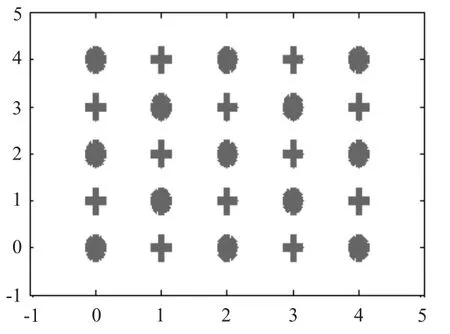
图1 平面上相间排列的25 点的两类点集Fig.1 25 points on a plane of two type point sets

1)选取惩罚因子C =10，径向基核函数参数σ = 0. 2，对该25 点的两类点集进行支持向量机及其改进算法的训练和测试分类实验，其在原始空间的分类曲线分布如图2 和图3 所示。其中图中圆点为正类目标，十字为负类目标，实线为最优分类曲线(二维情况下，分类曲面退化为分类曲线)。

图2 SVM 的分类曲线Fig.2 Classification curve of SVM

图3 改进算法的分类曲线Fig.3 Classification curve of improved algorithm

由对比可见，由于减少了约束条件，故获取了更宽的优化空间，在此模型参数下，改进算法的分类曲线对样本空间划分合理，分类均衡。

2)选取惩罚因子C = 10，径向基核函数参数σ = 0.55，对该25 点的两类点集进行支持向量机及其改进算法的训练和测试分类实验，其在原始空间的分类曲线分布如图4 和图5 所示。

由对比可见，此时改进算法可以对所有目标全部正确分类而原算法不能，因此改进算法获取了更为广阔的核函数模型寻优空间，更有利于核函数模型的参数寻优。

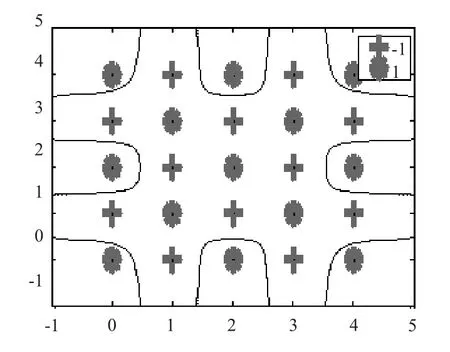
图4 SVM 的分类曲线Fig.4 Classification curve of SVM

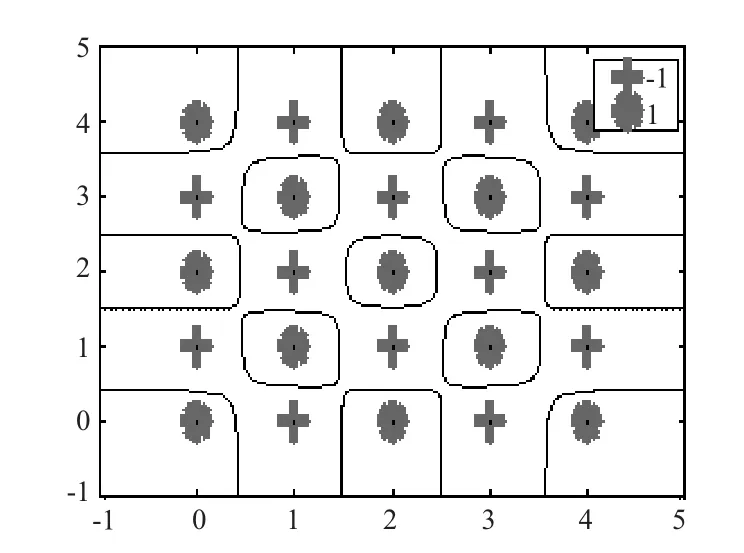
图5 改进算法的分类曲线Fig.5 Classification curve of improved algorithm

2.2 双螺旋线仿真数据分析

双螺旋线分类一直是模式识别领域公认的一个难题，它也因其难度而经常被用作检验模式识别算法性能的“试金石”［3］。该问题的分类要求是把x -y 坐标平面上2 条不同螺旋线的点正确分开。

双螺旋的平面坐标形式用如下的参数方程来表示:

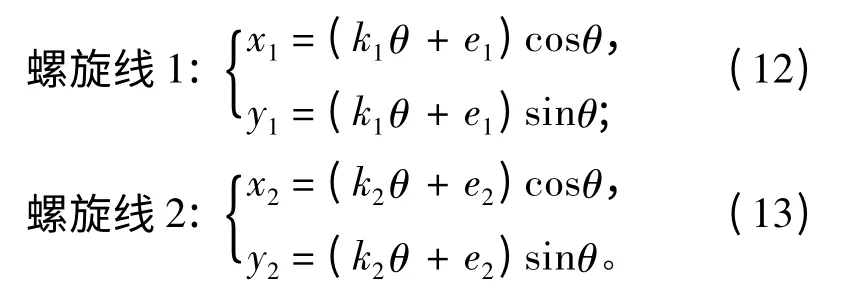
在本实验中，令k1=k2=2，e1=1，e2=3，θ∈［0，4π］。对每类在区间［0，4π］上等间隔采样126 个点，再在其中等间隔取26 个作为训练样本，其余100 个作为测试样本，因此共有52 个训练样本，200 个测试样本。

采用网格搜索法，惩罚因子C 取值范围为1 至100，步进为1;径向基核函数σ 的取值0.01 至1，步进为0.01，在100 × 100 的网格范围内，对双螺旋线数据样本进行训练和测试。

采用支持向量机算法，训练样本数据的错误率随参数C 和σ 的分布如图6 所示。

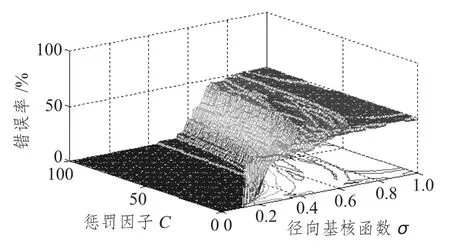
图6 SVM 算法中训练数据错误率分布Fig.6 The error rate distribution of SVM for training

采用改进的支持向量机算法训练样本数据的错误率随参数C 和σ 的分布如图7 所示。

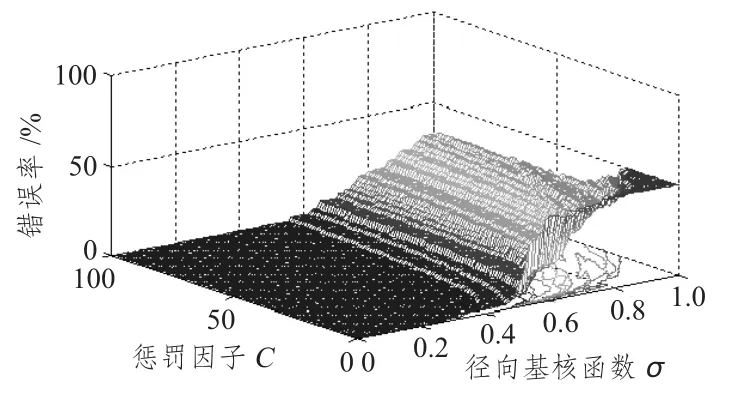
图7 改进算法中训练样本错误率分布Fig.7 The error rate distribution of improved for training

从训练样本的训练错误率随模型参数的变化来看，改进支持向量机在训练样本中，具备较宽的低错误率训练空间。

此时，采用支持向量机算法，测试样本数据的错误率随参数C 和σ 的分布如图8 所示。

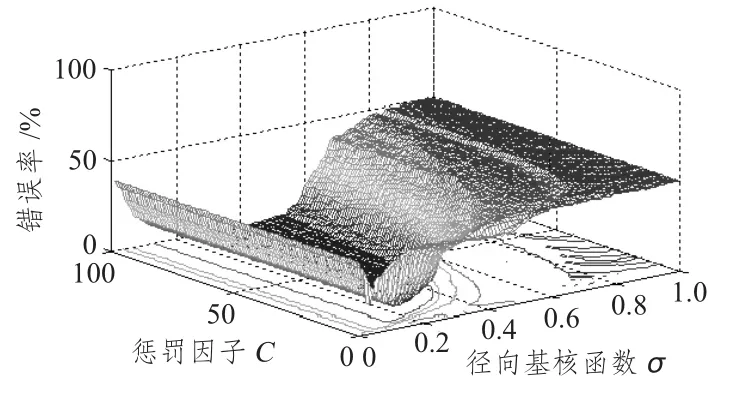
图8 SVM 算法中测试数据错误率分布Fig.8 The error rate distribution of SVM for testing

采用改进算法，测试样本数据的错误率随参数C 和σ 的分布如图9 所示。

从测试样本数据的测试错误率随模型参数的变化来看，改进支持向量机具备较宽的低错误率测试空间。

从仿真数据综合来看，改进的支持向量机算法性能较优。

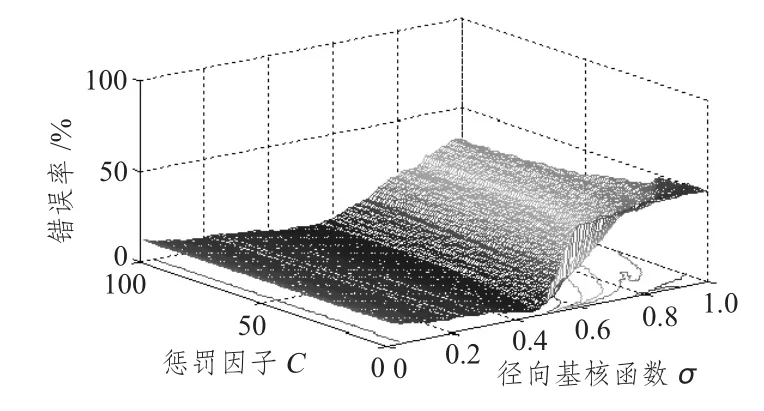
图9 改进SVM 算法中测试样本错误率分布Fig.9 The error rate distribution of improved SVM for testing

3 海上实测船舶噪声数据实验及分析

3.1 实验准备

目前，船舶螺旋桨桨叶数一般为3 叶、4 叶、5叶、6 叶和7 叶共5 类，根据桨叶数从3 叶到7 叶的顺序，可将舰船目标分为A ～E 五类。

桨叶数识别主要包括特征提取和分类识别两部分。在特征提取部分，通过对船舶目标辐射噪声进行DEMON 谱分析，提取DEMON 谱轴频的1 ～15 阶谐波线谱的幅度、线谱宽度，轴频的频率稳定度、幅度稳定度，谐波簇信噪比共33 维特征，进行归一化处理后作为桨叶数识别的特征。

进行试验的船舶目标辐射噪声样本全部为海上综合声呐听测波束实际录取的船舶目标噪声，试验样本的选取条件如下:

1)在综合声呐对噪声目标探测和稳定跟踪后输出得到的远场单目标噪声信号;

2)船舶目标噪声DEMON 谱中存在可见的调制线谱;

3)船舶目标的类型特征、桨叶数明确。通过样本选取共获取了3 725 个船舶目标噪声样本，按桨叶数进行分类，其中A 类样本1 466 个，B 类样本1 101 个，C 类样本570 个，D 类样本240 个，E类样本348 个。

3.2 桨叶数识别特征提取过程

对船舶辐射噪声依次进行带通滤波、检波、低通滤波、降采样、FFT 变换得到DEMON 谱［1］，如图10 所示，横坐标为频率，纵坐标为幅度。DEMON 谱中一般存在很多频率成倍数关系的谐波线谱，这组谐波中的第一根线谱频率对应螺旋桨转速。根据谐波线谱的幅度关系、宽度特征、稳定度、信噪比等特征，可以判断目标的类型，图10 为典型的B 类目标DEMON 谱图。

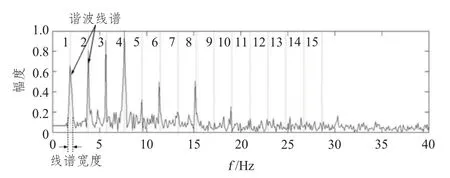
图10 某典型B 类目标DEMON 谱图Fig.10 A typical DEMON of target B

本文提取的目标类型识别特征是由以下5 部分特征组成的33 维特征矢量:

1)轴频的1 ～15 阶谐波线谱的归一化幅度大小;

2)轴频的1 ～15 阶谐波线谱的归一化宽度大小;

3)轴频的频率稳定性，本文以30 s 数据中轴频频率变化的方差作为频率稳定性特征;

4)轴频的幅度稳定性，本文以30 s 数据中轴频幅度变化的方差作为幅度稳定性特征;

5)谐波簇信噪比，本文以15 阶谐波线谱相对背景干扰线谱的突出程度作为信噪比特征。

据此对图10 所示DEMON 谱进行分析，得到33维桨叶数识别特征矢量如图11 所示。

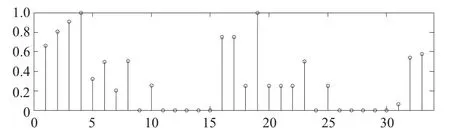
图11 33 维特征矢量示意图Fig.11 Schematic diagram of 33 dimension feature vector

3.3 船舶桨叶数分类实验及分析

将选取的目标噪声按类别随机分为对等的2 部分:一部分用来训练，另一部分用来测试，对支持向量机及其改进算法，以及神经网络算法进行对比。

支持向量机模型选取采用网格搜索法，惩罚因子C 取值为C =1.25k1，k1=1，2，…，20，径向基核函数的σ 取值为σ = 1.25k2/20，k2= 1，2，…，20，在20×20 的网格范围内，分别采用“一对一”、 “一对余”［8-10］的支持向量机多分类方法，分别进行目标类型识别的分类实验。

根据总样本的错误识别率最小原则［1］，分别获取支持向量机算法模型的最优参数，以此为训练参数，对目标样本进行10 次的随机分类实验，测试与训练样本各占50%。

同时对同一批数据，与应用最为广泛的BP 神经网络学习算法［11］进行了对比。BP 算法采用随机抽取50%样本训练，50%进行测试，通过综合考虑和模型寻优后，采用输入层为33 个神经元，中间层为12 个神经元、输出层为5 个神经元的3 层BP 神经网络进行了10 次分类实验。

最终统计获得在“一对一”、“一对余”的多分类方法下的支持向量机及其改进算法的对比，以及与BP 神经网络的实验结果如表2 和表3 所示。

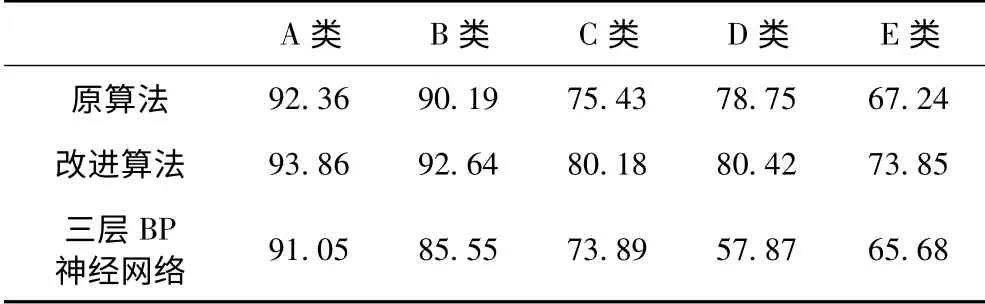
表2 基于“一对一”方法实验结果平均正确率比较Tab.2 Average correct rate on“one-versus-one”

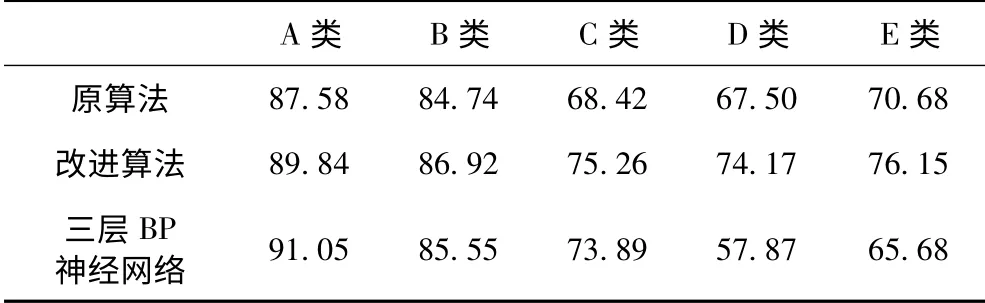
表3 基于“一对余”方法实验结果平均正确率比较Tab.3 Average correct rate on“one-versus-all”

由实验结果可知，在“一对一”、“一对余”模式下，改进支持向量机算法对相对于原支持向量机算法，以及BP 神经网络算法而言，具备较好的分类识别能力，性能较优。

4 结 语

通过理论分析、扩展的XOR 数据、双螺旋仿真数据和船舶辐射噪声DENOM 谱特征分类实验数据表明，对支持向量机在松弛变量和决策函数两方面进行改进而提出的基于径向基核函数的齐次决策二阶损失函数支持向量机改进算法，具有分类面划分合理、模型参数寻优空间广阔、总体分类性能优的特点，分类性能优于原支持向量机算法等分类算法，该支持向量机改进算法是一种适用于船舶螺旋桨桨叶数识别应用的有效的分类算法，实现了对船舶螺旋桨桨叶数的有效分类识别。

［1］戴卫国，程玉胜，王易川. 支持向量机对舰船噪声DEMON 谱的分类识别［J］. 应用声学，2010(3):206-211.DAI Wei-guo，CHENG Yu-sheng，WANG Yi-chuan.Classification of the DEMON spectra of ship-radiated noise based on Support Vector Machine［J］. Applied Acoustic，2010(3):206 -211.

［2］VAPNIK V N.统计学习理论的本质［M］.张学工，译.北京:清华大学出版社，2000.

［3］焦李成，周伟达，张莉.智能目标识别与分类［M］.北京:科学出版社，2010.JIAO Li-cheng，ZHOU Wei-da，ZHANG Li. Intelligent target identification and classification［M］.Beijing:Science Press，2010.

［4］邓乃杨，田英杰.数据挖掘中的新方法——支持向量机［M］.北京:科学出版社，2004.

［5］张春华.支持向量机中最优化问题的研究［D］.北京:中国农业大学，2004.

［6］陈宝林.最优化理论与算法(第2 版)［M］. 北京:清华大学出版社，2005.

［7］李明.详解MATLAB 在最优化计算中的应用［M］. 北京:北京电子工业出版社，2011.LI Ming. Application of MATLAB for Optimization Theory［M］. Beijing:Beijing Electronics Industry Publishing Press，2011.

［8］赵春晖，陈万海，郭春燕.多类支持向量机方法的研究现状与分析［J］.智能系统学报，2007，2(2):11 -17.ZHAO Chun-hui，CHEN Wan-hai，GUO Chun-yan.Research and analysis of methods for multiclass support vector machines［J］. CAAI Transactions on Intelligent Systems，2007，2(2):11 -17.

［9］黄勇，郑春颖，宋忠虎. 多类支持向量机算法综述［J］.计算技术与自动化，2005，24(4):61 -63.HUANG Yong，ZHENG Chuan-ying，SONG Zhong-hu.Multi-class support vector machines algorithm summarization［J］.Computing Technology and Automation，2005，24(4):61 -63.

［10］Vojtech Franc Vaclav HlavaC. Statistical Pattern Recognition Toolbox for Matlab User′s guide［R］.ftp://cmp.felk.cvut.cz/pub/cmp/articles/Franc-TR-2020-08.pdf.

［11］许东，吴铮.基于MATLAB6.X 的系统分析与设计——神经网络［M］. 西安:西安电子科技大学出版社，2003:19 -24.XU Dong，WU Zheng.System analysis and design based on MATLAB6. X［M］. Xi′an:Xi′an Electronic and Science University Press，2003:19 -24.