方形四立柱涡激运动及水动力性能分析

谷家扬，杨建民，渠基顺

(1．江苏科技大学 船舶与海洋工程学院，江苏 镇江，212003;2．上海交通大学 海洋工程国家重点实验室，上海200240)

0 引 言

由于平台多立柱之间的流动分离和剪切层干扰效应的复杂性，结构所受到的流体力与相关频率特性具有强烈的非线性特性，因此钝体的存在导致流场结构与受力特性变得更加复杂，且与单体结构有明显区别。目前，多个柱体之间的相互作用成为国内外学者研究热点。柱体排列方式主要有串列、并列和交错排列，不同排列方式对涡激运动的影响可参考相关文献［1－5］。在国内，李椿萱［6］研究了直径不同圆柱体的相互作用，研究发现当小圆柱体处于大圆柱体尾流一定的范围内能有效减少作用于大圆柱体上的外力。徐枫等［7］通过有限体积法求解二维不可压缩N －S 方程，对正三角形排列的等直径圆柱进行涡激振动的数值模拟，重点研究了间距比1.5 ～6.0 范围内，圆柱气动力响应和相关的频率特性、尾流流动模式的变化规律。吴波等［8］采用结构化网格和SST k－ω 湍流模型对海洋平台主四柱体结构物进行定常数值模拟，研究了不同来流角度及间距比组合下流场形式和水动力系数。

1 数值计算模型

本文研究对象为某深吃水四立柱平台。此平台由4 根立柱和4 个浮箱组成，四立柱平台模型示意图如图1 所示，俯视图尺寸如图2 所示。

图1 四立柱平台示意图Fig.1 Structure of platform with four columns

图2 四立柱平台主要尺寸Fig.2 Dimensions of platform

1.1 四立柱CFD 模型

本文运用Fluent 前处理软件Gambit 按1∶40 的比例建立二维四立柱模型，采用三角、四边形混合网格模型，近场区域使用致密的四边形网格，远场处采用相对稀疏的三角形网格。计算流域为50D ×30D，其中D为方柱边长。坐标原点位于上游两立柱中心点的连线中点处，原点离上游入口为15D，距离下游出口为35D。计算模型的全域网格和近场网格如图3 所示。

图3 方形四立柱整个流域网格和局部网格Fig.3 Computational grid of four square columns and close view of computaional grid

流体流动方向从左往右，流场左侧设定为速度入口，流场右侧设置为压力出口，相对压力选为0。流场上下边界设置为自由滑移壁面，四立柱模型的表面设置成无滑移边界。

采用SST k－ω 湍流模型和非稳态一阶隐式进行求解，动量方程的压力速度耦合采用SIMPLEC 算法，动量、湍流动能、耗散率项均采用二阶迎风格式以减少数值耗散。本文采用动网格技术来实现立柱和流体之间的耦合作用，在每个时间步内首先求解流体力学控制方程从而得到流体的速度场、压力场以及作用于立柱上的升力和拖曳力，通过UDF 获取作用在立柱上的流体力并将它带入结构动力学控制方程，利用自编的四阶Runge-Kutta 程序求得方柱运动响应，然后通过DEFINE_CG_MITION 宏函数将方柱运动响应传递给方柱并更新流场参数，开始新的循环。

本文计算模型特征值D = 0.435，质量比m*=0.72，固有频率fn= 0.061，且流向和横向平率比fnx/fny=1.0，折合速度范围U*=2.0 ～12.0。

1.2 网格敏感性测试

在使用CFD 对流场进行计算之前，网格质量测试是必不可少的一部分，本文网格测试结果如表1所示。3 种网格单元数不同，主要由进行四立柱周边网格划分时疏密程度决定。网格越密，精确度往往比较高，但是计算耗时较长。网格2 的计算结果和网格3 的计算结果比较接近，网格1 计算结果与后两者相差较大，考虑到模拟四立柱涡激运动的计算效率，采用网格2。

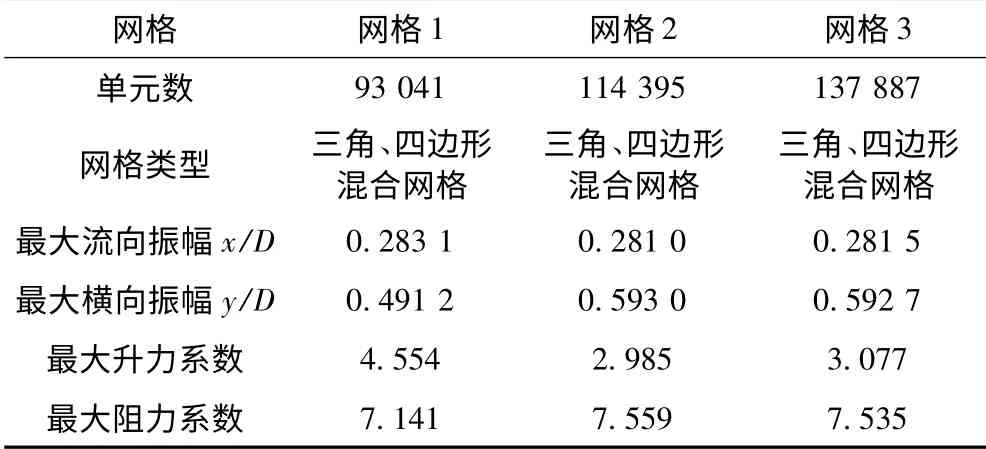
表1 网格敏感性测试Tab.1 The mesh sensitivity test

2 方形四立柱涡激运动响应

涡激运动特性重点关注运动最大响应振幅、升力系数频谱变化、运动轨迹和周围的流场特性。流动分离的分离点变化情况和柱体尾流的涡脱结构，可反映涡激运动在形成、发展、演化和稳定阶段的不同特征，进而对涡激运动响应进行预报。

进行医疗事故的界定时，这五个要件缺一不可。该《办法》所定义的医疗事故和台湾学者黄丁全[3]所定义的责任事故是同一范围，是个狭义上的医疗事故的定义，而广义的医疗事故也包括因为囿于当时的医疗技术和专业知识而造成的患者的人身伤害和死亡。有了医疗事故明确完整的定义之后，才可以对下一步的医疗事故的民事责任展开进一步的分析。

2.1 幅值响应与升力谱分析

本文采用最大振幅统计法和标称振幅统计法对振幅进行统计，具体公式如下:

最大振幅

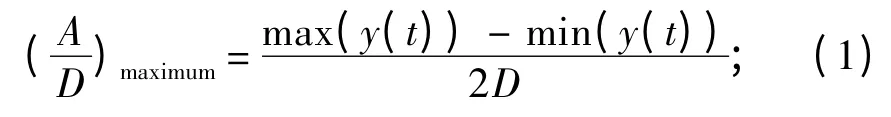
标称振幅

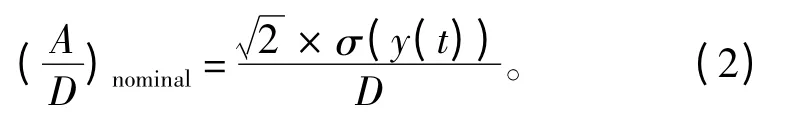
式中:max(y(t))为最大位移;min(y(t))为最小位移;σ(y(t))为位移标准差。

图4(a)为方形四立柱在不同折合速度下的流向幅值的变化情况，折合速度变化范围为2.0 ～12.0。从最大振幅统计结果来看，当折合速度为7.0 时，流向振幅达到了最大值，为0.32D;当折合速度12.0时，流向振幅达到0.31D。而从标称统计法的结果来看，当折合速度为11.0 和12.0 时，流向振幅达到0.20D。无论采用何种统计方法，流向振幅变化趋势是一样的，在折合速度不大于5.0 时，随着折合速度的增加，流向幅值逐渐增加，且增长的速度比较快。在折合速度为5.0 ～9.0 范围内，流向振幅小范围的振荡。随后，随着折合速度的逐渐增加，流向振幅缓慢增加。2 种方法统计结果的差距较大，其主要原因是方形四立柱流向运动的不稳定性。

图4(b)为方形四立柱涡激运动横向幅值随折合速度变化的情况。从最大振幅统计的结果可以看出，当折合速度为12.0 时，横向振幅达到最大值0.61D，其次为当折合速度为6.0 时，涡激运动横向振幅为0.59D。然而标称振幅统计法则不同，在折合速度为4.0 时，涡激运动的横向振幅达到最大，为0.44D。2 种统计方法的结果随折合速度的变化趋势也不相同。从标称振幅统计结果可以看出，折合速度4.0 是个拐点。当折合速度小于4.0 时，横向幅值随着折合速度的增加而增加;而当折合速度大于4.0 时，横向幅值随着折合速度先减小，然后缓慢上升。从最大振幅统计结果可以看出，当折合速度小于6.0 时，横向最大幅值随着折合速度的增大而增大，在折合速度7.0，8.0 和9.0 时运动幅值短暂的回落，随后随着折合速度的增加缓慢增大。在相同的折合速度下，流向幅值要比横向振幅小。

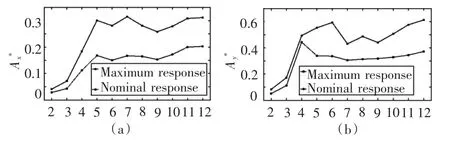
图4 不同折合速度下的振幅Fig.4 Stream-wise amplitude and transverse amplitude with reduced velocity

图5 为不同折合速度下流向振幅与横向振幅的时历曲线图，与其相对应的升力系数的频谱变换。论文截取了100 ～500 s 内稳定阶段的时历曲线图，当折合速度为4.0 时，横向位移在250 s 后时历曲线类似于正弦曲线进行周期性的运动，而流向位移曲线则没有横向位移的规整。当折合速度为7.0，9.0 和12.0 时，横向位移与流向位移的周期性较差，且运动不规律。横向位移在关于平衡位置在一定范围内波动，对于流向位移而言，当流体流过柱体，柱体在流向重新达到一个平衡位置，然后在新的平衡位置进行运动。从图中可以看出，随着折合速度的增加，流向新的平衡位置距离初始平衡位置的间距在增大。

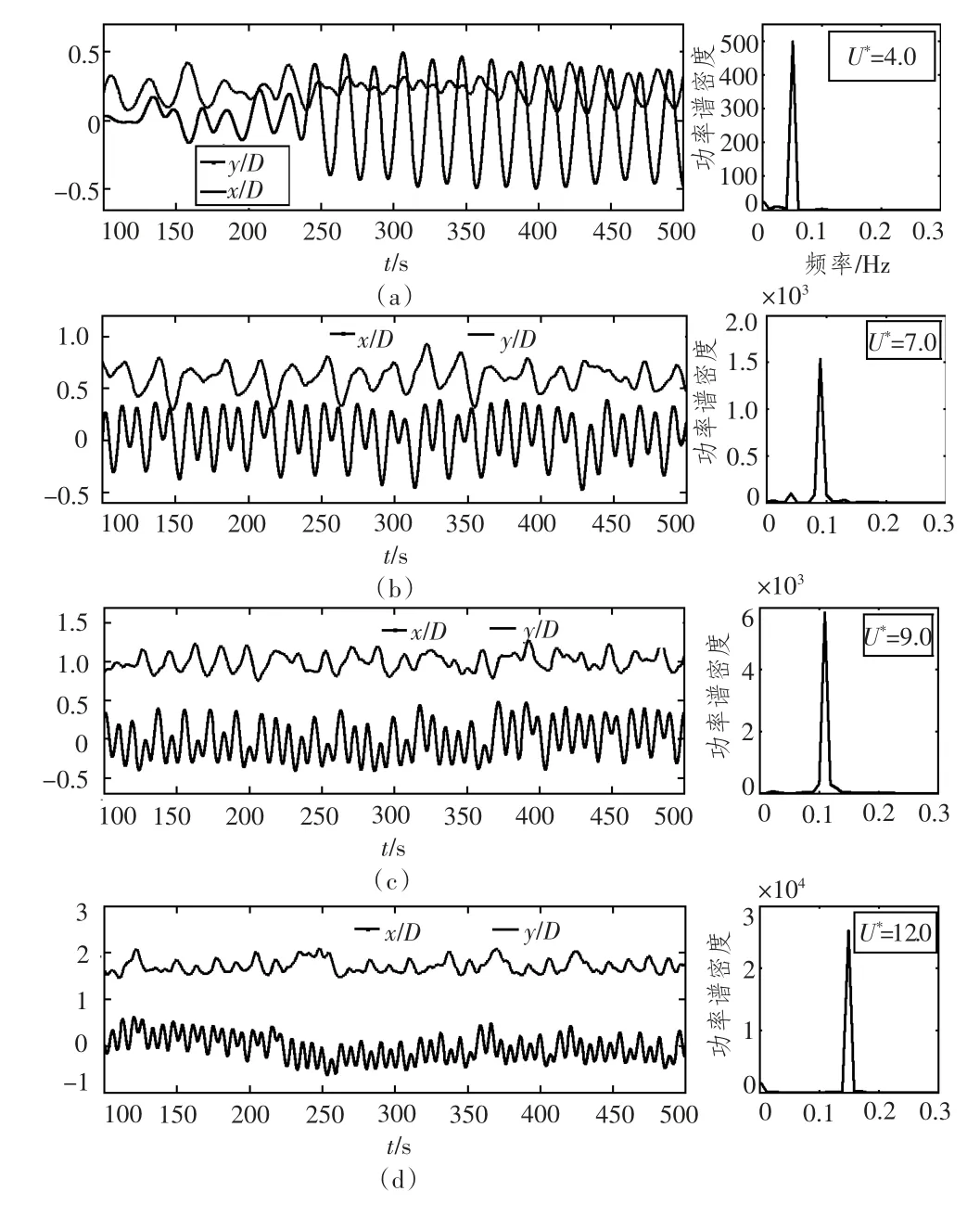
图5 不同折合速度下流向位移和横向位移时历曲线图与升力系数谱分析Fig.5 Time history of stream-wise displacement and tranverse displacement with reduced velocity，FFT analysis of total lift coefficient

谱分析是将数值模拟得到的升力系数的时历转化成系统能量在不同频率上的密度分布，从而将时域的结果转换到频域上进行分析。从谱分析的结果上看，在不同的折合速度下，系统只存在一个能量分布集中区域，即对应的升力系数主频率只有一个。另外，随着折合速度的增大，升力系数对应的主频率的数值也在增大。

从图6 可看出，横向振动频率与折合速度的关系，f*为柱体实际振动频率与其固有频率的比值。随着折合速度的增加，柱体的振动频率也在不断增大，并没有发现经典圆柱涡激运动的锁定区间。柱体的横向振幅与流向振幅也没有锁定在某一值附近。因此可以得出结论，方形四立柱不存在频率锁定现象。

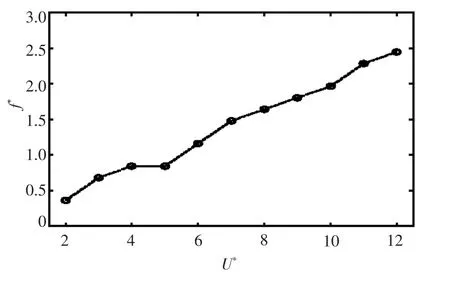
图6 不同折合速度下运动频率Fig.6 Frequency response with reduced velocity

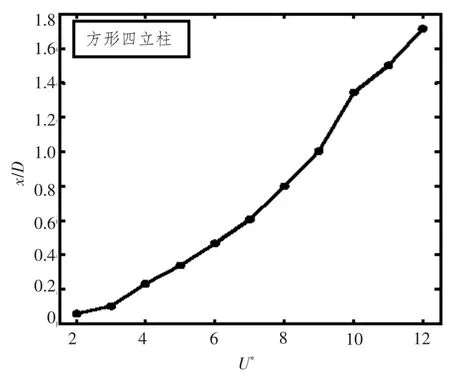
图7 不同折合速度下流向平衡振幅Fig.7 The equilibrium postion of stream-wise oscillation

方形四立柱流向运动平衡位置随折合速度的变化如图7 所示。从图中可看出，方形四立柱的平衡位置随着折合速度成线性变化关系。流速的持续增大，使得所处流向平衡位置远离初始位置。

2.2 运动轨迹

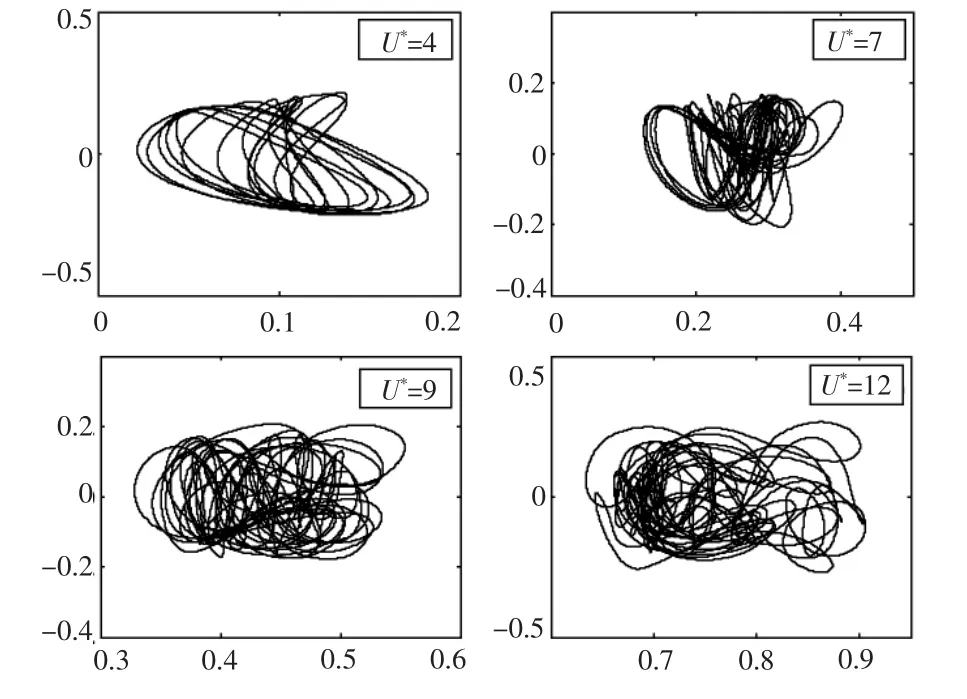
图8 不同折合速度下方形四立柱轨迹图Fig.8 Four square column motion trace at various reduced velocity

图9 不同折合速度下圆形四立柱轨迹图Fig.9 Four cylinder column motion trace at various reduced velocity

两自由度四立柱涡激运动的轨迹和单柱体涡激运动的轨迹并不相同，由于柱体之间的相互影响，轨迹图没有单柱体有较强的规律性。方形四立柱与圆形四立柱运动轨迹如图8 和图9 所示，方形四立柱运动轨迹规律性很差，这可从横向位移曲线与流向位移曲线可以看出。由于圆形四立柱的横向位移曲线和流向位移曲线比较规则，另外流向的振动频率是横向振动频率的2 倍，导致了圆形四立柱的运动轨迹出现了经典的“8”字形。在不同的折合速度下横向位移与流向位移的大小不同，引起“8”字形肥瘦程度不同。

2.3 尾涡特性

方形四立柱尾涡模式如图10 所示，截取了6 个典型折合速度下的方形四立柱尾涡结构图。由于柱体之间的干扰作用，下游的2 个柱体处于上游2 个柱体的尾流中，方形四立柱在典型折合速度下的尾涡模式总体呈现出2P 模式。

3 结 语

本文采用有限体积法结合四阶Runge-Kutta 方法对方形四立柱涡激运动进行数值模拟，通过DEFINE_CG_MOTION 宏函数将求解出的结构动力瞬态响应传递给立柱，使用动网格技术来实现网格的更新，重点分析了四立柱两向自由度的幅值响应、频谱特性、运动轨迹和尾涡脱落模式，得出如下结论:

1)在折合速度2.0 ～12.0 下，方形四立柱涡激运动流向最大位移为0.31D，横向最大位移为0.61D。

2)方形四立柱的横向运动频率随着折合速度的增加而增大，没有出现频率锁定现象。

3)相比于圆形四立柱运动轨迹出现了经典的“8”字形，方形四立柱的轨迹图较为紊乱。

4)方形四立柱在不同折合速度下的尾涡模式总体呈现出2P 模式。

［1］SUMNER D，RICHARDS M D．Some vortex-shedding characteristics of the staggered configuration of circular cylinders［J］． Journal of Fluids and Structures，2003，17(3):345 －350．

［2］SUMNER D．Closely spaced circular cylinders in cross-flow and a universal wake number［J］． Journal of Fluids and Structures，2004，126:245 －249．

［3］SUMNER D，RICHARDS M D，AKOSILE O O．Two staggered circular cylinders of equal diameter in cross-flow［J］．Journal of Fluids and Structures，2005，20(2):255－276．

［4］PRICE S J，PAaOUSSIS M P，KRISHNAMOORTHY S．Cross-flow past a pair of nearly in －line cylinders with the upstream cylinder subjected to a transverse harmonic oscill-ation［J］．Journal of fluids and structures，2007，23(1):39－57．

［5］LAM K，JIANG G D，LIU Y，et al．Simulation of cross-flowinduced vibration of cylinder arrays by surface vorticity method［J］．Journal of fluids and structures，2006，22(8):1113 －1131．

［6］李椿萱，彭少波，吴子牛．附属小圆柱对主圆柱绕流影响的数值模拟［J］． 北京航空航天大学学报，2004，29(11):951 －958．LI Chun-xuan，PENG Shao-bo，WU Zi-niu．Numerical study of flow around a main cylinder by controlled satellite cylinders［J］． Journal of Beijing University of Aeronautics and Astronautics，2004，29(11):951 －958．

［7］徐枫，欧进萍．正三角形排列三圆柱绕流与涡致振动数值模拟［J］．空气动力学学报，2010，28(5):582 －590．XU Feng，OU Jin-ping． Numerical simulation of vortex －induced vibration of three cylinders subjected to a cross flow in equilateral arrangement［J］． Acta Aerodynamica Sinica，2010，28(5):582 －590．

［8］吴波，缪泉明，周德才，等．四柱体结构物流场干扰与水动力特性研究［J］．水动力学研究与进展，2013，28(5):597－605．WU Bo，MIAO Quan-ming，ZHOU De-cai，et al． Numerical analysis on flow interaction and hydrodynamic characteristic of four-column structure［J］．Chinese Journal of Hydrodynamics，2013，28(5):597－605．