基于参数化子模型的SWATH船典型节点抗疲劳设计
2015-12-19任慧龙张清越胡雨蒙江雪云
任慧龙,张清越,胡雨蒙,江雪云
(1.哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨150001;2.哈尔滨工程大学 多体船技术国防重点学科实验室,黑龙江 哈尔滨150001)
0 引 言
小水线面双体船(small waterplane area twin hull ship,SWATH)是近年来发展起来的一种新概念船型,因其良好的耐波性及快速性,以及能够胜任多种工作的优点而受到广泛关注[1-2]。但与此同时,为SWATH 船型带来诸多优势的细长支柱体结构同样是整船中结构最为薄弱的部位。特别是连接桥过渡区域,由于截面发生突变,刚度不连续,应力场不连续[3],使得该区域在横浪和斜浪状态下不断受到较大的交变横向对开力和片体不同步纵摇扭矩的作用,应力水平很高,应力集中显著。此外,SWATH船型对于重量的变化非常敏感,船体结构的尺寸不宜过大,因此这些高应力部位通常都会使用高强度钢来满足其屈服和屈曲强度要求。综上所述,SWATH船型连接桥过渡区域的疲劳强度问题十分突出,在结构设计初期就应该予以足够的重视。文献[4]对多种影响船体结构应力的相关因素进行比较分析,提出一种小水线面双体船典型节点的抗疲劳设计,为设计者提供参考;文献[5]针对小水线面双体船采用规范法、谱分析法、设计波法进行疲劳强度评估,并对其中的关键节点进行了以满足疲劳强度为目标的优化设计,取得了一定的成果。
通常设计者依据规范和经验拟定的结构形式和构件尺寸未必能够满足结构强度的要求,而小水线面双体船的相关规范尚不完善,且疲劳强度和结构细节密切相关,对于疲劳载荷和结构应力响应的估算十分困难,疲劳寿命的准确计算还有赖于水动力和有限元分析技术。基于疲劳强度分析的优化设计是给出较好抗疲劳结构方案的有效途径,但此方法需要对优化模型进行大量的迭代计算。针对这些问题和难点,本文提出一种结合参数化子模型有限元分析方法和基于Miner 线性累积损伤理论及Weibull分布连续模型的疲劳设计波法的优化方法,通过快速生成批量模型的参数化建模技术,准确描述局部模型外载荷的子模型法及能够较好反映结构细节而计算量又相对较小的疲劳设计波分析方法来快速有效地解决结构抗疲劳设计问题。
1 参数化子模型法
参数化子模型法是针对局部结构优化问题提出的一种快速准确的有限元计算方法,它基于整体结构模型的有限元分析,从计算结果中提取局部模型切割边界的位移作为约束条件施加在子模型上,从而得到子模型较为精确的外载荷响应计算结果。通过参数化建模手段建立子模型的参数化模型,使优化模型的大量迭代计算得以实现。
1.1 整船有限元分析
SWATH 船型结构特殊。较小的船长型深比,深入水下的潜体使得SWATH 船的纵弯曲强度有较大的富裕。但较大的侧面积,重力浮力沿船宽分布情况和薄弱的支柱体结构使其在遭受横浪时产生对开弯矩作用及斜浪航行时产生复杂扭转的情况下非常危险。特别是连接桥过渡结构,主要承受了巨大的交变载荷,很容易发生疲劳破坏。
本文依据CCS 颁布的《小水线面双体船指南2005》[6]中的相关要求,使用通用有限元软件MSC. Patran 建立某小水线面双体船整船有限元模型,计算应力云图如图1 所示。在初期的总强度分析计算中,可以发现该船的高应力区域集中在支柱体横舱壁(或横框架)上端与舷台相交的结构过渡处。特别是在横浪工况下,该区域的应力水平很高,应力集中严重,如图2 所示。因此,可将此局部结构作为疲劳强度校核和优化的典型节点。

图1 整船计算应力云图Fig.1 Stress calculation of whole ship
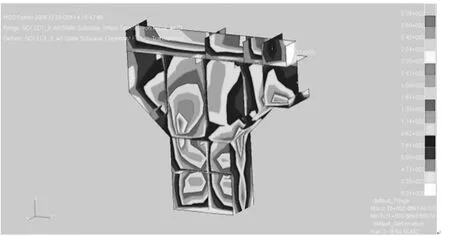
图2 舷台与支柱体横舱壁应力云图Fig.2 Stress calculation of typical detail
1.2 子模型法
子模型法基于圣维南原理,即如果实际分布载荷被等效载荷代替后,应力和应变只在载荷施加的位置附近有改变,因此只要子模型切割边界避开载荷集中及应力集中位置,子模型内部就可以得到较精确的解[7]。子模型法包含以下步骤:
1)整体模型分析,对整体粗网格模型进行计算分析,并算出局部模型切割边界的位移响应;
2)根据结构实际构造建立局部精细网格模型;
3)根据整体模型分析切边的位移响应通过线性插值法加载至局部精细子模型的边界,作为其边界条件;
4)局部精细模型自身的载荷及边界条件不变,进行有限元分析。本文从MSC. Patran 整船有限元计算结果中提取切割边界位移响应,采用APDL 参数化编译语言编写了Ansys 子模型自动加载接口,为后续用以优化迭代计算的参数化模型提供准确的外载荷模拟。
1.3 参数化模型
参数化模型是一种通过变量参数及建模命令建模,可以快速生成系列模型的技术手段,它包含几何模型参数化生成,有限元网格参数化划分,材料属性参数化定义,载荷和边界条件自动添加及参数化后处理等几块内容。本文采用Ansys 参数化编译语言APDL 建立小水线面双体船连接桥过渡区域典型节点的参数化模型,选择影响该区域疲劳强度的几何参数和尺寸参数作为优化变量,为后续的优化迭代计算打下基础。本文建立的局部结构参数化模型和子模型法加载计算应力结果如图3 和图4 所示。
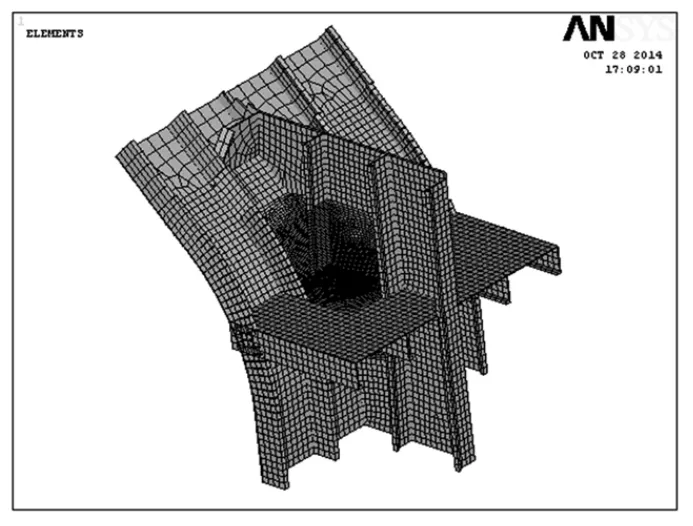
图3 参数化子模型效果图Fig.3 Parametric sub-model
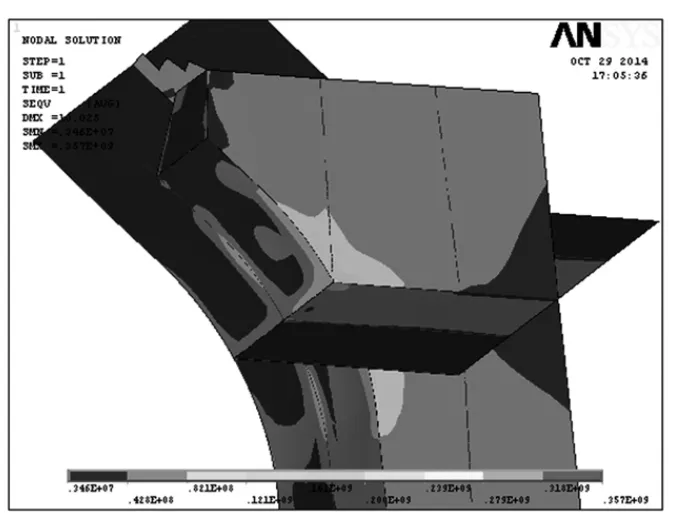
图4 参数化子模型计算应力云图Fig.4 Stress calculation of parametric sub-model
2 典型节点疲劳强度分析
基于谱分析的疲劳评估直接计算虽然具有较高精度,但是需要对波浪谱有效波浪频率范围内的多个规则波和浪向角分别进行计算,计算量过于庞大,优化模型的迭代计算难以实现;而基于经验公式的规范简化计算方法虽然计算简便,但是不涉及有限元分析计算,难以体现结构的细节特征;CCS 《小水线面双体船指南2005》中的载荷计算简化公式及有限元加载方式虽然已经较充分地考虑到了SWATH 船的结构及载荷的特点,但针对尺度相近的具体船型却难以体现不同SWATH 船的差异性。综上所述,研究认为基于设计波法的疲劳评估直接计算方法通过势流理论及船舶航行过程的实际海况长期分析得到设计波载荷并通过有限元分析计算得到典型节点的疲劳应力范围,能够反映结构的细节特征,疲劳载荷更加真实,而计算量又相对较小,适合进行优化迭代计算。
2.1 设计波系统的确定
根据CCS《小水线面双体船指南2005》中规定的载荷工况及总强度计算结果,认为SWATH 船主要考虑的载荷参数为:横向对开弯矩、不同步纵摇扭矩、纵向弯矩、水平扭矩、纵中剖面剪力。由文献[5]及文献[8]的计算结果可知在横浪产生的横向对开力作用下产生的累积损伤在SWATH 船型的整个疲劳寿命周期内占主要成分,其余载荷的累积损伤相对较小,可以忽略。考虑到本文的最终目的是针对SWATH 船连接桥过渡区域的结构进行抗疲劳设计,仅以横浪状态下的横向对开弯矩作为主要载荷参数的设计波计算结果已经能够表征结构的疲劳强度。指南中规定了横浪状态的时间分配系数为0.25。
根据本研究所自主开发的基于三维势流理论的波浪载荷计算程序计算船体在单位波幅规则波下的波浪载荷传递函数,根据全球波浪散布图及数理统计理论进行主要控制载荷的长期预报,取10-8概率水平的预报值作为疲劳载荷设计值。主要控制载荷的幅频响应最大值对应的浪向即为设计波的浪向β和ω,而设计波的波长为:

设计波的波幅为载荷设计值与主要载荷参数幅频响应最大值之比:

2.2 S - N 曲线选取
结构在某一应力范围水平为S 的单一循环载荷作用下达到疲劳破坏所需循环次数为N,则称该结构在应力范围水平为S 时的疲劳寿命为N,一般根据疲劳试验结果拟合得到S - N 曲线,记为:

式中,m 和A 为疲劳试验所得参数。
对上式等号两边取对数,得
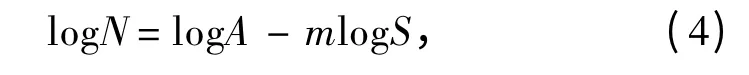
即为常用的S-N 曲线的双对数线性模型。CCS《船舶结构疲劳强度指南》[9]中给出了8 条S-N 曲线对应的参数值及焊接和结构形式。但SWATH 船型连接桥过渡处的结构在规范中无法找到对应的结构形式,S-N 曲线需由疲劳试验确定。在此取文献[10]中的SWATH 船连接桥过渡结构疲劳试验结果作为疲劳评估的S-N 曲线。
2.3 应力范围的Weibull 分布
在疲劳评估的设计波法中,设计寿命期应力范围的长期分布定义为Weibull 分布,分布函数见下式:
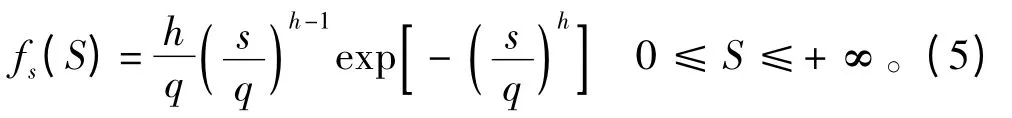
式中:h 为形状参数;q 为尺度参数。根据CCS 《小水线面双体船指南》,h =1 比较有意义。q 则可以用回复期内超越概率为P(S ≥SL)=1/NL的应力范围SL来表示:
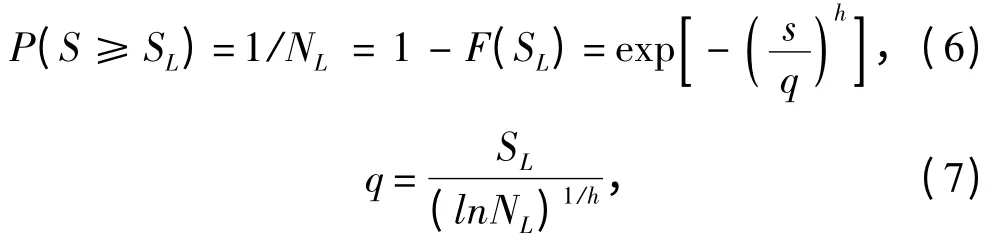
式中:NL为回复期内的应力范围循环次数,依据CCS 《船舶结构疲劳强度指南》,对于设计寿命为20 年的舰船,应取0.6 ×108。同时该指南中规定应力范围应在t × t 的精细网格有限元模型下按Lagrange 插值计算得到的热点应力,插值方法如下:
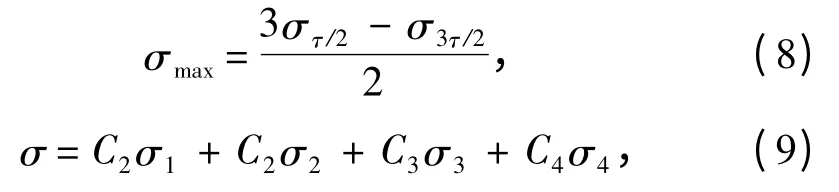
其中στ/2和σ3τ/2都是按式(9)计算得到的,式(9)中的σ1、σ3、σ4是靠近焊趾的4 个有限元节点的应力值,而系数C1、C2、C3、C4按下式计算:

式中:x 为插值点到焊趾的距离;xi为有限元节点到焊趾的距离。
2.4 累积损伤度的计算
Weibull 应力范围分布模型对应的线性累积损伤度可以表示为:
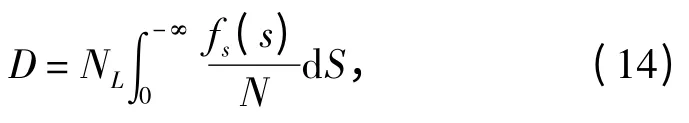
代入式(3)和式(5)可得:
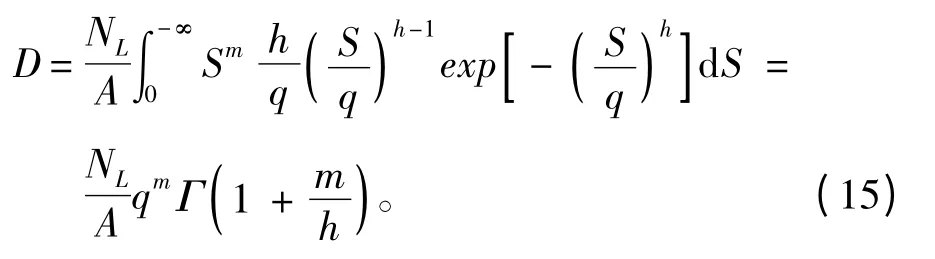
对应的GAMMA 函数值可通过查表得到。
3 优化模型
在进行结构优化分析中,必须要建立合适的数学优化模型。一个完整的数学优化模型包括所定义的目标函数、优化变量及约束条件等。通常数学优化模型可以表示为如下形式:
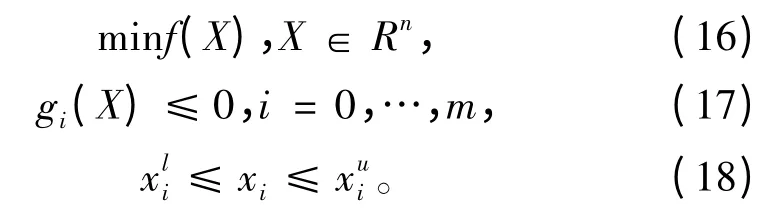
式中,X=(x1,x2,…,xm)T为设计变量组成的列向量空间;f(X)为定义的目标函数;gi(X)为定义的约束函数,包括等式约束和不等式约束;和分别为设计变量xi的上下限值,其大小通常可以根据实际设计情况而定。
针对本文中的抗疲劳设计问题,目标函数取为结构的累积损伤度D。连接桥过渡区域的圆弧半径越大,结构过渡就越平滑,显然疲劳强度更高,但是过大的圆弧半径对于SWATH 船的重量控制和阻力性能都不利;过渡区域的构件尺寸设计未必最合理,部分区域的构件尺寸对于结构强度的贡献并不明显。因此,优化变量取连接桥过渡区域的圆弧半径R 及该区域各板构件的厚度ti。同时,对于SWATH 船这类吃水对结构重量非常敏感的船型,尽量地减轻船体重量非常必要,在优化时还应以结构重量作为优化模型的约束条件。数学优化模型表示如下:
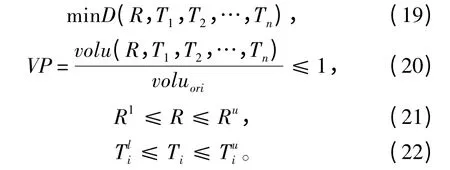
式中:VP 为体积参数,是优化后体积与初始体积之比;R 为过渡圆弧的半径;Ti为各板构件厚度。
4 优化结果与分析
本文选取的算例为某5 000 t 级SWATH 船,根据前文所述的方法及理论建立目标船的参数化模型及优化模型,在Ansys 的优化设计平台中进行优化迭代计算。优化算法选择为零阶子问题逼近法,此方法迭代效率较高,且不容易陷入局部最优解,能够满足本次优化迭代的要求。目标函数、优化变量和约束条件的选取和初始值见表1。
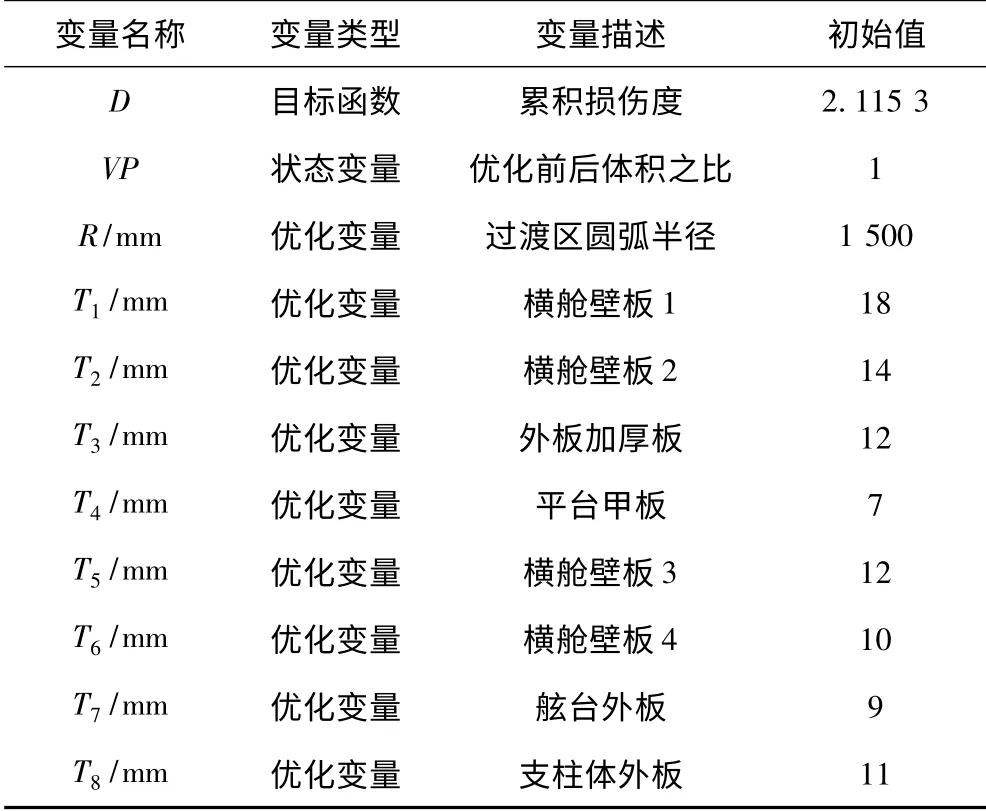
表1 各变量初始值Tab.1 The initial value of the variables
经过28 步优化迭代,计算收敛。目标函数值随迭代序列对变化如图5 所示,部分迭代序列的计算结果见表2。
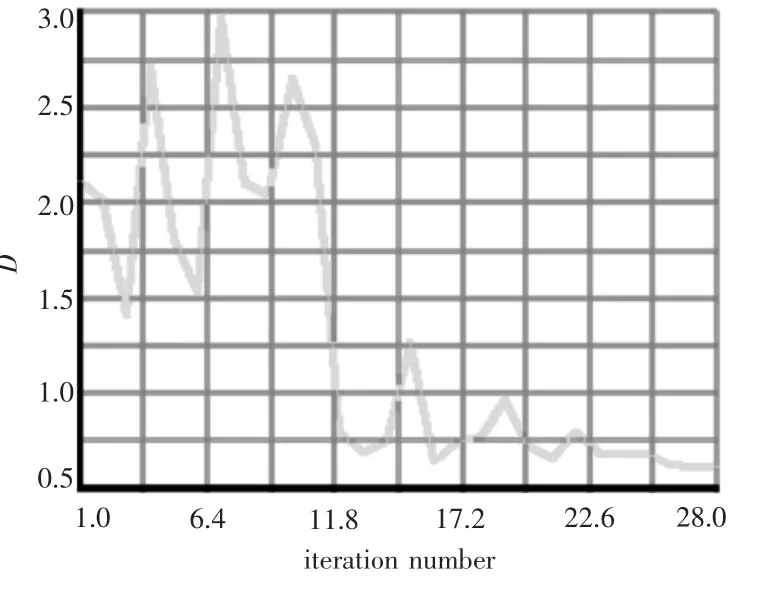
图5 目标函数随迭代序列变化Fig.5 Optimization iteration of objective function
表中的优化序列28 即为本次优化的最优设计方案。累积损伤度降低为0.62,大大提高了结构的疲劳寿命,同时局部结构重量还有一定的降低。
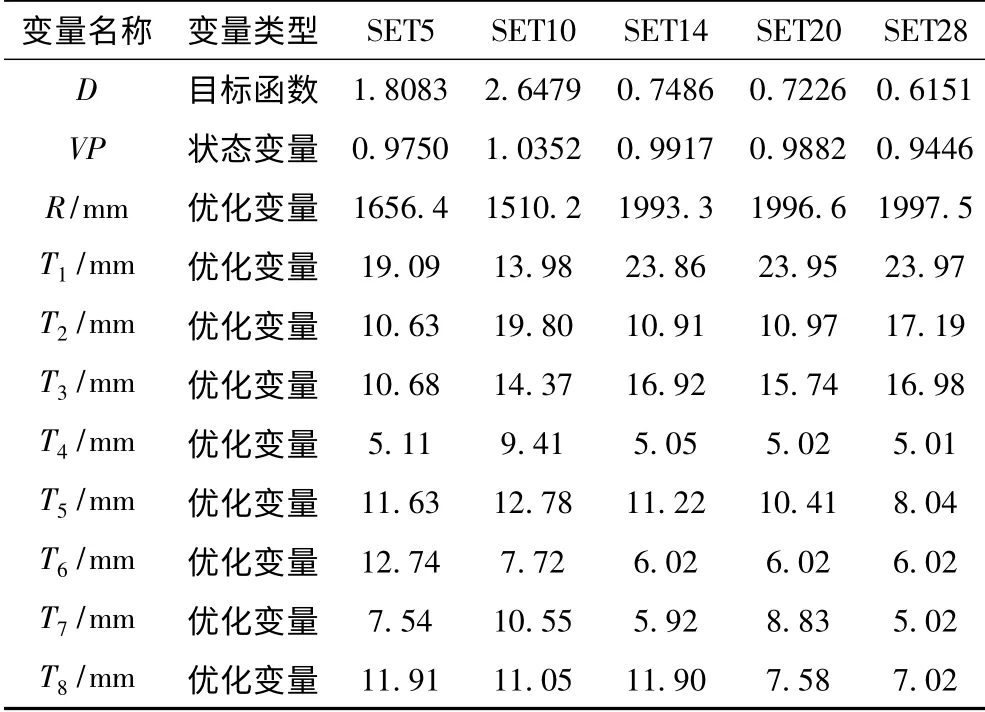
表2 部分迭代序列计算结果Tab.2 Partial results of optimization iteration
从优化结果中可以发现,过渡圆弧半径的增大对于降低该区域应力集中的作用非常明显。同时,靠近应力集中点的横舱壁板1、横舱壁板2、外板加厚板的尺寸对累积损伤度的影响也很明显。相对的,远离应力集中点的构件尺寸对于疲劳强度的贡献比较低,可以适当减小尺寸。从理论上分析,SWATH船的支柱体结构在横浪作用下类似于一个深入水下的悬臂梁,一端受到与梁相垂直的力的作用。决定支柱体上端与舷台连接处应力集中水平的主要因素就是该区域的几何连续程度和水平剖面的抗弯刚度。因此,提升该剖面上的构件尺寸能够提高抗弯刚度;而增大过渡圆弧的半径不仅能够使几何过渡更加平滑,同时也增大了剖面尺寸。
5 结 语
本文基于参数化子模型法及疲劳强度评估的设计波法,提出了一套结构抗疲劳设计的优化方法,并结合某SWATH 船进行优化设计,得出以下结论:
1)参数化子模型法为局部结构应力响应的准确计算和优化迭代问题提供了有效途径;
2)基于设计波法的疲劳强度评估方法能够真实反映结构细节,同时计算量较小,适合作为结构设计初期的抗疲劳设计衡准;
3)SWATH 船连接桥过渡区域的疲劳强度问题严重,增加过渡圆弧的半径和应力集中点附近的板材厚度对提高该结构疲劳强度帮助较大,本文提出的抗疲劳设计方案为SWATH 船连接桥过渡区结构设计提供了一定参考。
[1]林伟国,朱云翔,范井峰,等.小水线面双体船的发展及在海军舰船领域中的应用前景[J].船舶,2007,18(3):1-5.LIN Wei-guo,ZHU Yun-xiang,FAN Jing-feng,et al. Development of small waterplane area twin hull and its application prospect in navy[J].Ship and Boad,2007,18(3):1-5.
[2]ANANTHA S V.Numeric design and evaluation of swath form[J].International Shipbuilding Progress,2002,49(2):95-125.
[3]徐志亭,柳存根,王晓宇.小水线面双体船疲劳强度的规范计算法研究[J].中国造船,2011,52(4):66 -73.XU Zhi-ting,LIU Cun-gen,WANG Xiao-yu. Research on rules′ method in fatigue assessment of SWATH[J].Shipbuilding of China,2011,52(4):66 -73.
[4]陈颖,岳亚霖,崔维成.小水线面双体船典型节点抗疲劳设计[J].舰船科学技术,2010,32(6):8 -13.CHEN Ying,YUE Ya-lin,CUI Wei-cheng. Anti-fatigue design of SWATH typical local details[J].Ship Science and Technology,2010,32(6):8 -13.
[5]徐志亭.小水线面双体船结构疲劳分析及典型节点优化研究[D].上海:上海交通大学,2011.
[6]中国船级社.小水线面双体船指南[S].北京:人民交通出版社,2005.ChinaClassification Society.Guid elines of Small Waterplane Area Twin Hull Craft[S].Beijing:China Communication Press,2005.
[7]史战新.基于Ansys 子模型法的肘板结构优化[J].舰船科学技术,2014,36(8):19 -26.SHI Zhan-xin. The bracket structure optimization based on Ansyssub-model method[J].Ship Science and Technology,2014,36(8):19 -26.
[8]甄春博.小水线面双体船结构疲劳评估方法研究[D].哈尔滨:哈尔滨工程大学,2009.ZHEN Chun-bo.Study on the methodofthe structural fatigue assessment of SWATH[D]. Harbin:Harbin Engineering University,2009.
[9]中国船级社.船舶结构疲劳强度指南[S].北京:人民交通出版社,2007.China Classification Society.Guidelines for fatigue strength of ship structure[S].Beijing:China Communication Press,2005.
[10]甄春博,任慧龙,冯国庆,等.小水线面双体船连接桥结构疲劳强度试验[J].哈尔滨工程大学学报,2012,33(4):414-418.ZHEN Chun-bo,REN Hui-long,FENG Guo-qing,et al.Fatigue strength test of a SWATH ship′ s cross-deck structure[J]. Journal of Harbin Engineering University,2012,33(4):414 -418.
