附加质量对水中平面板振动噪声特性的影响
2015-12-19于丹竹
于丹竹,黎 胜
(大连理工大学 船舶工程学院,辽宁 大连116024)
0 引 言
舰船结构振动噪声通常以水中板的振动声特性研究为基础。而船作为一个相对庞大的工业产品,所用板材在加工过程中并非严丝合缝精致细密,其中有大量的焊点焊缝是不能够被光滑处理的,而板材中也夹杂着相当数量的不光滑部分。这些凸起和粗糙部分称之为板材的附加质量,而往往正是这些被忽略的附加质量,引起了板材的异常噪声和振动。这些粗糙在生产过程中不能够避免,而同时又会对振动噪声特性构成影响,因此研究附加质量对水中平板振动噪声特性的影响规律以及附加质量对主结构固有特性的影响具有探索性意义。
目前,在这一领域已有多位学者涉足。Pierce等[1]提出了内部带有模糊内部构件的结构的基本结构-声模型。在这一模型的内部带有一个模糊的结构,由随机布置的一系列点连接的弹簧质量系统构成。该理论预报了在某些条件下统计平均值可以近似计算模型的特性。Y. k. Lin[2]提出由于模糊子系统将引起的结构阻抗的标准偏差变化。通过在频域内对随机散布点上子系统的固有频率进行建模,研究了附加的不确定多重子系统对主体结构特性的影响。S. C. Conlon and S. A. Hambric[3]研究了附带有简单的和复杂附件的轻质多层板的阻尼和诱导阻尼。他们对带有集中质量和复杂的附件轻量级的航天用板的阻尼进行了多种测量,实验研究并采用了简单的统计能量分析模型。黎胜和李贤徽[4]研究了分散布置的质量对板的声辐射特性的影响。分析模型显示了附加质量载荷的尺寸和布置位置对板声辐射特性的影响。
本文对带有附加质量平板的有限元模型进行分析。将有限元法和Rayleigh 积分结合,用于求解流固耦合问题并获得耦合系统的响应。研究不同重量和分布情况的附加质量对主结构的影响,及其随激励频率的变化规律。
1 流体加载板的声辐射理论
1.1 平面板的有限元方程
结构所受到的随时间变化的简谐激励力为。在其作用下结构考虑流体加载作用的有限元动力方程为:

式中:Z=(-ω2M +iωC +K)/iω 为阻抗矩阵;M,C和K 分别为质量阵、阻尼阵和刚度阵;ω 为激励圆频率;v 为节点速度矢量;fe为激励力向量为激励点坐标,fp为由结构表面声压引起的流体对结构的作用力。
1.2 流体介质场的瑞利积分
由于简谐振动板表面为一个半无限域,因此任何一场点处声压可由瑞利积分公式得到[5-6]
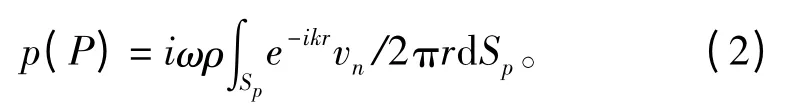
式中:ρ 为水的密度;vn为板表面Sp上节点法向振动速度向量。为Sp上任意点。
当P ∈Sp时,对板表面进行离散,对各单元代入结构法相速度和表面声压,则式(2)可写为节点法向速度vn和表面声压p 的关系为:

其中:D 为声阻抗矩阵。
1.3 结构-声耦合方程和声辐射
结构表面节点法向速度向量vn与节点速度向量v 之间的转换关系为:

同时有结构表面声压p 引起的声压载荷速度fp写成矩阵形式为:

式中:G 为方向余弦转换矩阵;A=∫SNTNdS,N 为形状函数矩阵。则可得结构-声耦合方程为:
求得节点速度向量v 之后,进而vn和p 也可求解获得。
当表面声压p 和表面法向速度vn求解之后,结构的辐射声功率可以有式(7)求得:
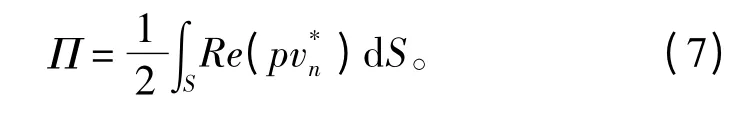
为了进一步研究附加质量对主结构的影响,通过模型降阶法(ROM)对流体加载平板模型的固有参数进行估算。通过模型降阶法可以还原出外力作用下耦合系统的模态频率和阻尼系数。
2 模态参数估算
通过流固耦合系统的单元质量阵和刚度阵可以建立模态参数的降阶模型[7]:
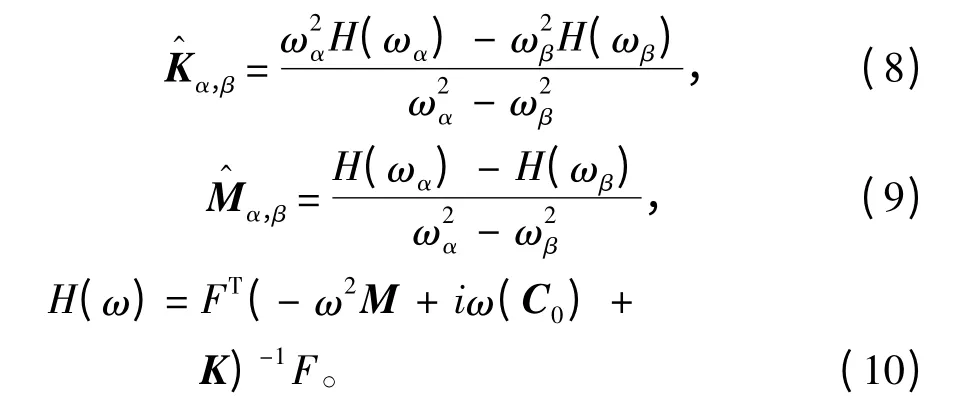
式中:C0=C + GAZGT。ωα和ωβ为计算频段内的插值频率。计算频段内降阶模型的质量阵和刚度阵求得后,通过求解和的广义特征值问题,即可获得如流体加载平板的固有频率和结构阻尼系数等模型的参数。
3 数值分析
板的尺寸为Lx= 0.455 m,Ly= 0.379 m,h =0.003 m,钢材质平面板的密度ρs= 7 850 kg/m3,杨氏模量E = 2.1 ×1011N/m2,泊松比ν = 0.3。水介质密度ρ = 1 000 kg/m3,水中声速c = 1 500 m/s。用Mindlin 板单元建模,将其划分为 的网格,节点自由度数为803。
附加质量以2 种不同的散布形式随机布放在板表面,如图1 所示。图中灰色部分为附加质量。本文分别计算了3 种不同总质量的附加质量,以便研究附加质量的总质量对主结构的影响规律。附加质量的总质量分别占主结构原质量的10%,50%和100%。
数值计算结果显示,附加质量的不同总质量和散布情况,对主结构的影响情况有所不同,并且随着外部激励力的频率增高,影响效果有较大变化。
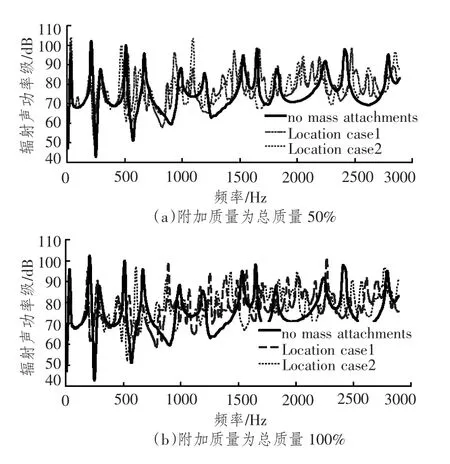
图3 辐射声功率级随附加质量工况变化Fig.3 Sound radiation power level vary with the location case
辐射声功率级随附加质量总重量不同的变化情况如图2 所示,可以看出当总质量增加时,附加质量对主结构的影响增大,并且总质量越大,使得主结构的固有平率峰值点左移,因此,将是主结构更容易激发出低阶模态。同时振动引起的辐射噪声随着总质量增加而增大,其中890 Hz 增幅100%总质量与无附加质量结构振动辐射噪声相比增幅达到38 dB。
辐射声功率级随附加质量散布位置不同而变化情况如图3 所示,由于附加质量的总质量相同以50%和100%总质量为例,而只是散布位置不同,因此主结构的振动噪声辐射幅值增幅区别并不明显,但是主结构辐射声压级随频率变化曲线峰值点偏移现象明显,因此可知附加质量总重量不变对频域内总辐射声压及幅值影响无明显区别,但是将改变主结构固有频率是指产生不同的偏移。
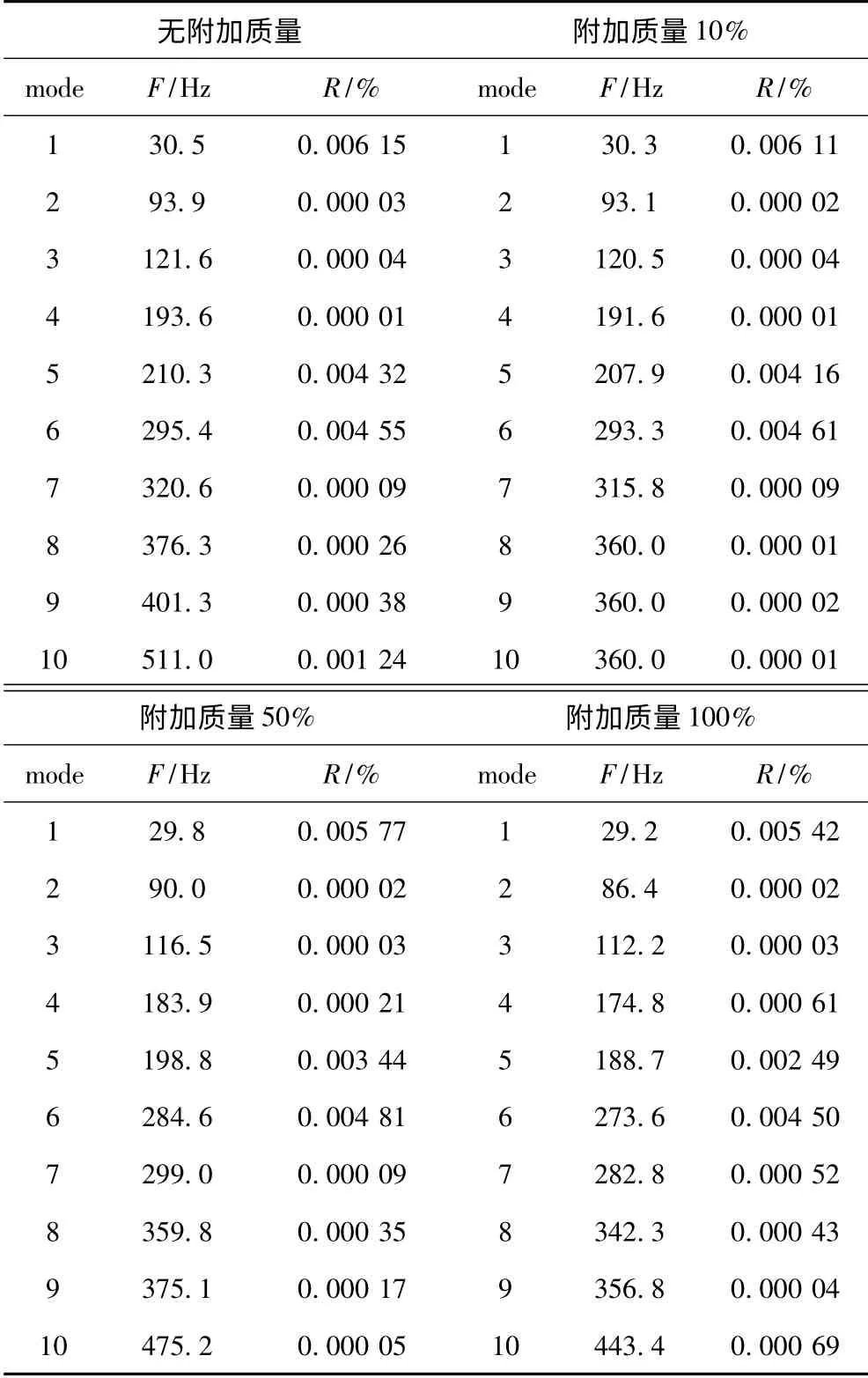
表1 降阶模型的固有频率及阻尼系数Tab.1 The natural frequencies and modal damping ratios of the modes
因此,为进一步探讨附加质量对结构固有频率和主结构本身特性的影响,本文通过流固耦合系统的单元质量阵和刚度阵建立了模态参数的降阶模型,并估算了带有附加质量的平面板的固有频率和结构阻尼系数等模型的参数,通过表1 给出。由表中可以清楚地看出,由于附加质量总重量的增加结构的固有频率有所降低,低阶固有频率降低不明显,均在1 Hz 以内,但高阶固有频率降低非常明显尤其是第10 阶固有频率,总质量增加50%结构第10 阶固有频率降低将近32 Hz。
随着总质量的增加阻尼系数基本也随之呈现递减的趋势,个别有所增加,其中附加质量10%与无附加质量结构的阻尼系数相比减幅较大。
4 结 语
本文以水中障板为例,对由不同分布情况的附加质量所引起的水中平面板声-振特性的变化进行数值分析。通过建立有限元模型,将其与声流体介质的瑞利积分相互耦合用于求解流固耦合问题,以获得耦合系统的响应。进一步通过模型降阶法求解由附加质量所引起的结构模态参数变异。计算结果表面附加质量对主结构声振特性具有一定的影响,随着总质量的增加,影响增强,结构辐射声压级随总质量增加而增大,并且结构固有频率随之降低,辐射声压级随频率变化曲线峰值点左移。当附加质量总质量不变而散布位置发生改变时,结构辐射声压级幅值变化不明显,但结构固有频率发生较大改变,峰值点均出现不同偏移。通过建立模态参数的降阶模型得到结构固有频率阻尼系数等参数,也证明同样现象。
[1]PIERCE A D,SPARROW V W,RUSSELL D A.Fundamental structural-acoustic idealizations for structures with fuzzy internals[J]. Journal of Vibration and Acoustics,1995,117:339-348.
[2]LIN Y K.On the standard deviation of change-in-impedance due to fuzzy subsystems[J]. J. Acoustic. Soc. Am,1997,101(1):616-618.
[3]CONLON S C,HAMBRIC S A. Damping and induced damping of a light weight sandwich panel with simple and complex attachments[J]. Journal of Sound and Vibration,2009,322:901 -925.
[4]LI X,LI S. The effects of distributed masses on acoustic radiation behavior of plates[J]. Applied Acoustics,2008,69:272 -279.
[5]FAHY F.Sound and structural vibration:radiation,transmission and response[M].London:Academic Press,1993.
[6]澳·诺顿. 工程噪声和振动分析基础[M]. 盛元生等,译.北京:航空工业出版社,1993:113 -115.NORTON M P. Engineering noise and vibration analysis[M].Beijing:Aviation Industry Press 1993:113 -115.
[7]LI X,LI S. Modal parameters estimation for fluid-loaded structures from reduced order models[J]. Journal of the Acoustical Society of America,2006,120:1996 -2003.
