双掠结构旋翼桨叶动力学特性研究
2022-04-24夏双满林长亮王金亮张体磊
夏双满,林长亮,王金亮,张体磊
(1.航空工业哈尔滨飞机工业集团有限责任公司飞机设计研究所,哈尔滨150066)(2.陆军装备部航空军事代表局哈尔滨地区航空军事代表室,哈尔滨150066)
0 引言
进入21 世纪以来,直升机产业迅猛发展,在各行各业都发挥着重要作用。随着直升机技术的不断发展,直升机在性能、操纵品质、舒适性、可靠性和效率等方面都取得了长足进步。但直升机的噪声和振动水平相对于固定翼飞机还有很大差距,降低直升机的噪声和振动水平已成为现代直升机研发的首要目标。
旋翼桨叶的设计,特别是桨尖的结构形式,对直升机的性能、振动和声学都有很大影响。具有代表性的旋翼桨叶是欧直公司H160 型机的“Blue Edge”(蓝色刀锋)桨叶,该桨叶是基于双掠形式设计的,具有一定的前掠角度和后掠角度,这种结构形式在降低桨叶BVI(桨涡干扰)噪声的同时,还能降低机体的振动水平。
国内外针对桨尖结构对动力学的影响进行了大量研究。M.Filippi 等利用梁单元和六面体单元建立了复合材料桨叶三维有限元模型,准确地预测了复合材料双掠桨叶的应力分布;H.Thomas等开展了直梁桨叶和桨尖后掠桨叶在悬停状态下的气弹稳定性试验研究,结果表明,在悬停状态下,直梁桨叶的阻尼要大于桨尖后掠桨叶;张俊豪等研究了双掠桨叶的无轴承旋翼直升机气动机械稳定性,系统地分析了桨尖前掠、后掠、下反和上反等几何参数对无轴承旋翼直升机地面共振和空中共振的影响;H.Yeo 等分别运用一维梁模型和三维有限元模型建立桨叶模型,并对比了两种方法求解固有频率的差异;R. Celi 等推导了一种适用于后掠桨尖的桨叶有限元建模方法,研究发现,后掠桨尖的引入导致了挥舞、摆振和扭转模态之间的强耦合;K.Kim 等研究了桨尖后掠角等参数对旋翼桨叶气弹响应的影响;K.Yuan 等研究发现,对桨尖的后掠角、下反角等参数进行联合优化设计可以有效降低旋翼振动载荷;M. Ku‑mar 等研究发现,双掠桨叶结构形式会导致桨叶根部的摆振力和扭转力矩增加。从上述文献可以看出,针对双掠桨叶,国外主要是在噪声、气弹响应等方面进行了深入研究,而针对双掠角度等几何参数对固有频率的影响公开报道较少;国内针对桨叶的动力学特性方面的研究主要集中在常规直梁桨叶,并未对双掠结构桨叶的动力学特性进行系统地研究,特别是未对前掠角度和后掠角度等结构参数对桨叶动特性的影响进行分析。
本文运用Harmilton 原理推导出桨叶的运动方程,采用有限元法对旋翼系统进行简化,通过求解广义特征值问题,得到桨叶的各阶固有频率,系统研究不同前掠角度和后掠角度对桨叶动特性的影响,在此基础上,分析整体配重对桨叶调频的作用。
1 旋翼动力学方程
采用有限元法对桨叶运动方程进行空间离散,把桨叶划分成若干个梁单元,则整个桨叶总势能的变分可以表示为
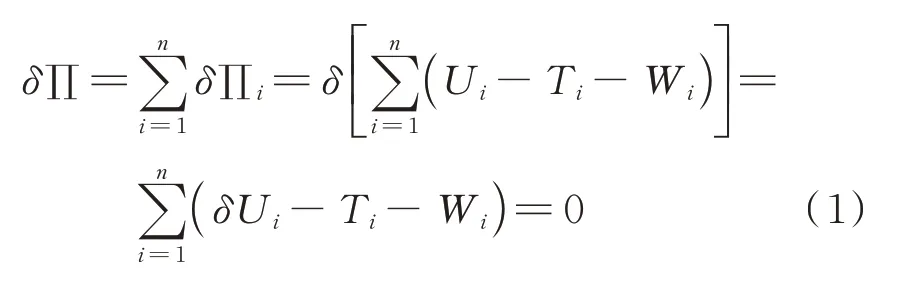
空间离散形式的Harmilton 原理为
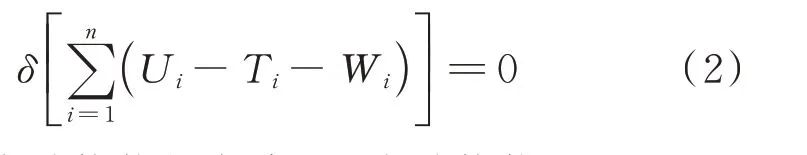
式中:∏为总势能的变分;∏为总势能;U、T、W分别为桨叶的应变能、动能和外力功。
经过推导,可以得到准线性化的一片桨叶的运动方程
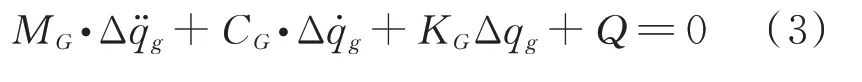
式中:Δ̈、Δ̇、Δq为对广义变量的差分。
忽略运动方程(3)中的阻尼项和外力项,则旋翼动力学的自由振动方程为
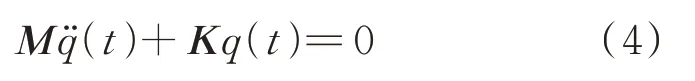
式中:和分别为质量阵和刚度阵,一般为对称正定矩阵,为对称半正定矩阵。
假定系统运动的广义坐标为如下形式:
=sin(-) (5)
式中:为阶矢量;为矢量振动的频率;为时间变量;为由初始条件确定的时间常数。
将式(5)带入式(4),可得:
-=0 (6)
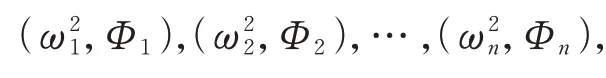
2 双掠桨叶动力学特性
2.1 桨毂结构形式
桨叶连接在不同构型的桨毂上,其动力学特性有明显差别,以星形柔性桨毂为例,双掠桨叶与星形柔性桨毂连接,主桨毂由具有4 个支臂的星形件和4 副夹板以及连接星形件和夹板的球形轴承和频率匹配器组成,如图1 所示,图中1 为桨毂星形件,由模压的玻璃纤维和环氧树脂叠层结构组成;2 为层压弹性体轴承,是星形桨毂的核心,承受桨叶所有运动载荷,起到挥舞、摆振和变距铰的作用;3 为夹板,由预浸带、泡沫填块、碳纤维蒙皮等复合材料模压制成;4 为频率匹配器,也叫黏弹减摆器,主要是一层黏弹性的硅橡胶块,通过剪切变形提供摆振阻尼,同时也附加了弹性约束;5 为自润滑自定位轴承,位于星形件支臂末端桨叶夹板中心。
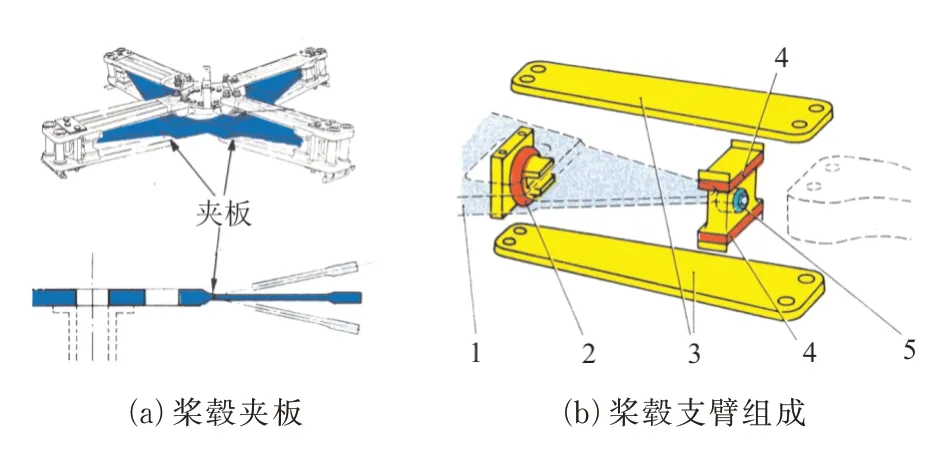
图1 主桨毂结构示意图Fig.1 Schematic diagram of hub structure
桨叶的挥舞运动是桨叶连同一对夹板绕弹性体轴承中心做上、下运动,而在挥舞方向刚度很小的柔性臂随其弯曲变形,这样可将弹性体轴承当作挥舞铰,在铰上附加弹性约束。
摆振运动是桨叶连同一对夹板一起绕弹性体轴承前后摆动,柔性臂在摆振方向的刚度远远大于其挥舞方向刚度,通过较柔性臂刚度低的频率匹配器的剪切变形提供了摆振阻尼,同时又在桨根附加弹性约束,可调节桨叶摆振固有频率。这样可将弹性体轴承认为摆振铰,铰上附加有弹性约束。
2.2 双掠桨叶剖面刚度
复合材料桨叶剖面特性包括桨叶挥舞刚度、摆振刚度、扭转刚度、弹性中心和剪切中心,这些动力学参数是桨叶设计最基本的原始参数,也是开展桨叶动力学特性分析的基础,桨叶剖面特性的准确性是正确研判直升机旋翼动力学特性的前提。由于直升机旋翼复合材料桨叶剖面构造复杂:其典型剖面包括前缘包铁、包铁下垫布、蒙皮、单向预浸带大梁,多数桨叶还有中间支撑梁、后缘支撑梁、后缘加强条以及前缘配重和整体配重,为了满足强度、刚度、弦向重心的要求和桨叶挥舞、摆振和扭转三者间的耦合,本文采用有限元法计算桨叶剖面特性。
本文研究的双掠桨叶为复合材料铺层结构,主要包括预浸带大梁、前缘附预浸带、蒙皮、泡沫填块、内部加强梁(包括前U 形梁和后U 形梁)、整体配重、末端配重以及桨尖结构等。旋翼半径为6 m,分为桨叶内段、前掠段和后掠段。桨叶在0.7处前掠,前掠角度为7.7°,桨叶在0.95处后掠,后掠角度为44.4°。桨叶结构示意图如图2所示。

图2 桨叶结构示意图[15]Fig.2 Schematic diagram of blade structure[15]
通过自编程序自动选取若干个桨叶典型剖面,将桨叶剖面分为上蒙皮、下蒙皮、C 形大梁、前U 形梁和后U 形梁等结构,并划分网格,典型剖面有限元网格如图3 所示。

图3 桨叶典型剖面有限元网格Fig.3 Finite element mesh of typical blade section
剖面刚度计算结果如图4~图6 所示,可以看出:桨叶挥舞弯曲刚度和扭转刚度沿展向逐渐变小,而摆振刚度受铺层增/减影响明显;桨尖区域的摆振刚度快速下降,同时挥舞刚度和扭转刚度也同步下降。
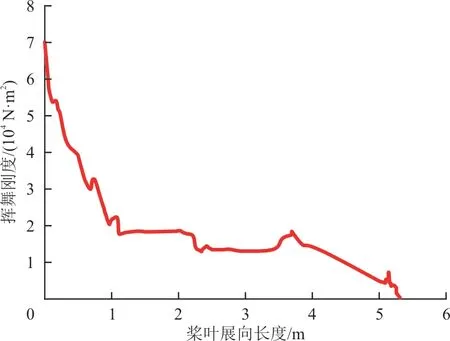
图4 挥舞弯曲刚度Fig.4 Flap bending stiffness
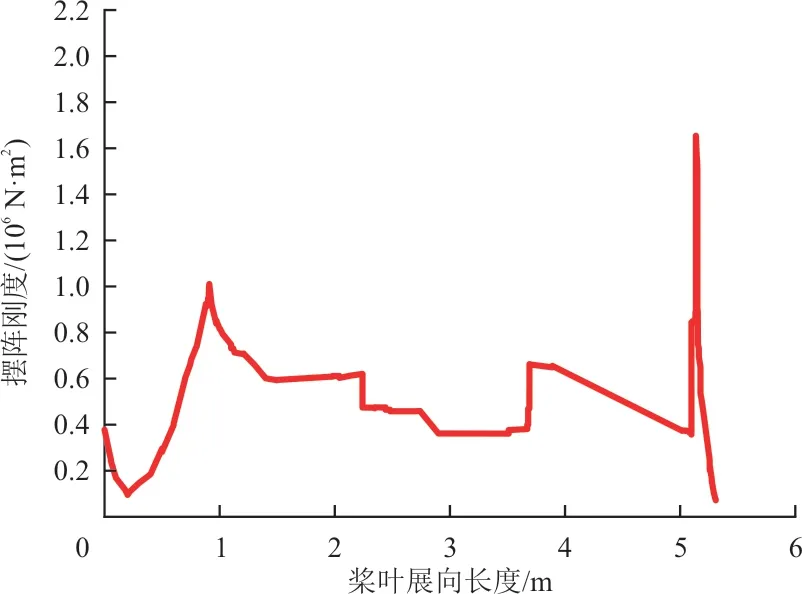
图5 摆振弯曲刚度Fig.5 Lag bending stiffness
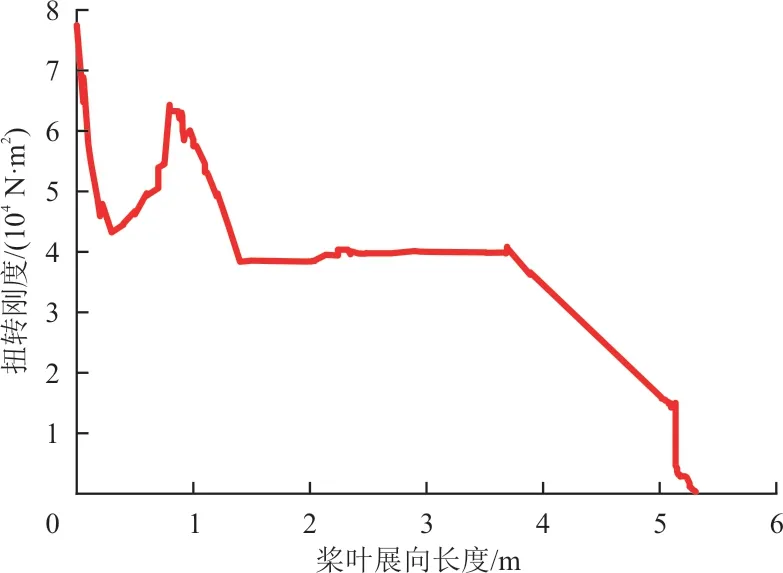
图6 扭转刚度Fig.6 Torsional stiffness
前掠角度、后掠角度、前掠站位和后掠站位等参数未改变桨叶内部结构,对桨叶的挥舞弯曲刚度、摆振弯曲刚度和扭转刚度无影响,但是双掠角度改变了桨叶剖面1/4 弦线和轴线相对于桨叶参考线弦向的位置,按照以下两种情况具体分析:一是前掠角度不变,后掠角度从30°变化至44.4°;二是后掠角度不变,前掠角度从6.7°变化至8.7°。计算结果如图7~图10 所示。
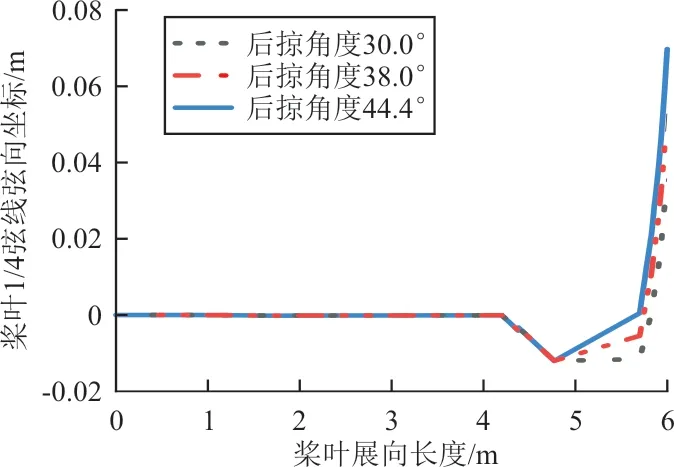
图7 1/4 弦线弦向坐标随后掠角度变化Fig.7 1/4 chord coordinate v.s. swept-back angle
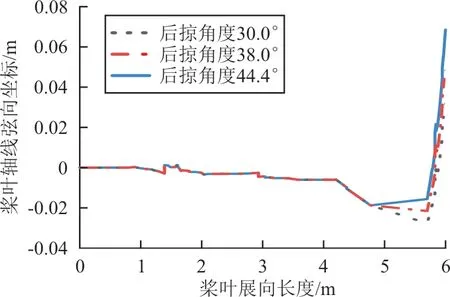
图8 轴线弦向坐标随后掠角度变化Fig.8 Axis coordinate v.s. swept-back angle
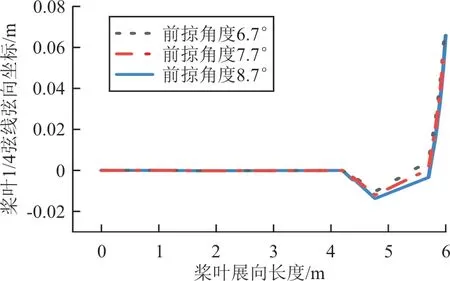
图9 1/4 弦线弦向坐标随前掠角度变化Fig.9 1/4 chord coordinate v.s. swept-forward angle
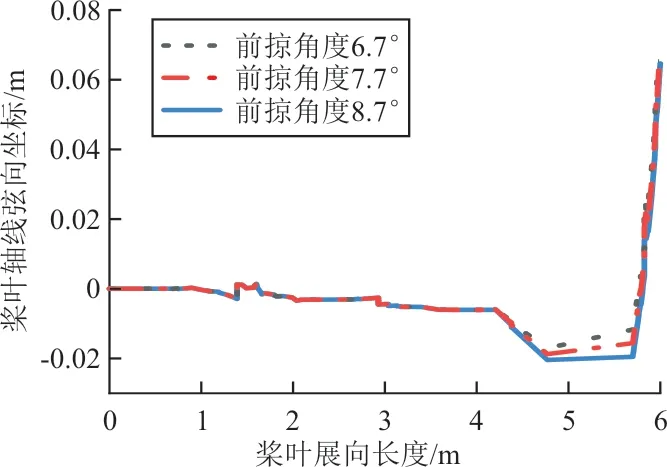
图10 轴线弦向坐标随前掠角度变化Fig.10 Axis coordinate v.s. swept-forward angle
从图7~图8 可以看出:桨叶在4.2 m 处开始前掠,在5.52 m 处开始后掠,并随着后掠角度的变化,1/4 弦线和轴线的弦向位置同时发生改变。
从图9~图10 看出:随着前掠角度的改变,桨叶1/4 弦线和轴线的弦向位置在桨叶前掠站位开始发生变化。
综上,前掠角度和后掠角度对桨叶固有频率会有一定的影响。
2.3 双掠桨叶动特性
双掠桨叶特殊的桨叶形式使得桨叶各阶模态均与扭转运动产生强烈的耦合。由于高阶谐波激振力在振动响应中的影响较小,实际中对于大于8 Ω 的激振力频率一般不考虑。本文列出前七阶固有频率,后掠角度不变,前掠角度变化时桨叶各阶模态频率如图11 所示,前掠角度不变,后掠角度变化时各阶模态频率如图12 所示。
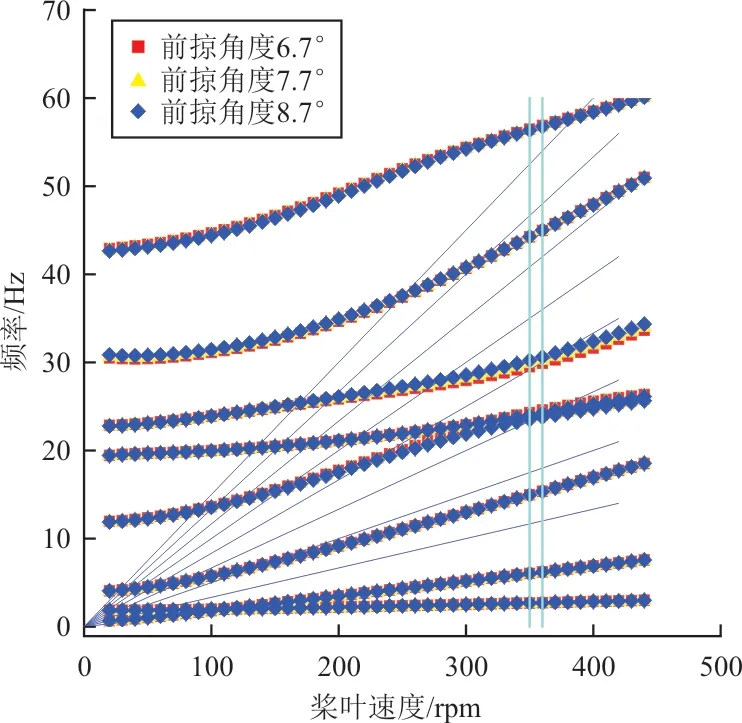
图11 不同前掠角桨叶共振图Fig.11 Diagram of rotating frequencies with different sweep-forward angle
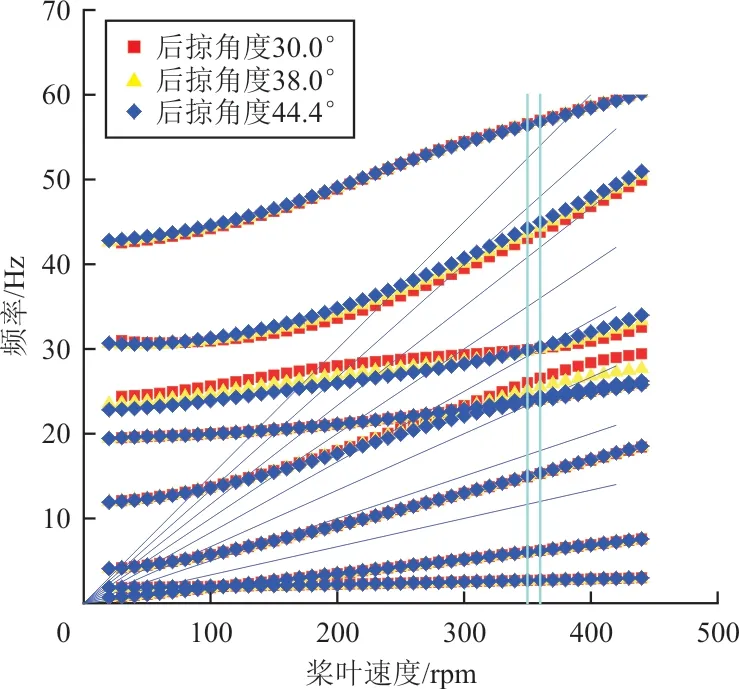
图12 不同后掠角桨叶共振图Fig.12 Diagram of rotating frequencies with different sweep-backward angle
从图11~图12 可以看出:前掠角度和后掠角度的变化对桨叶在工作转速下的前三阶固有频率影响较小,基本未发生变化,表明前掠角度和后掠角度所引起的扭转运动与桨叶低阶模态的耦合程度较低;四阶以上各阶频率随着前掠角度和后掠角度变化而变化,但是变化幅度不大。
2.4 双掠桨叶动特性参数分析
在桨叶的各阶固有频率配置确定之后,可以通过改变桨叶的质量分布以及挥舞、摆振和扭转刚度分布,使桨叶的前三阶挥舞频率、前二阶摆振频率和一阶扭转频率配置更加合理。以桨叶前掠7°和后掠30°结构形式为例,分析整体配重对桨叶动力学特性的影响。带配重前后桨叶的质量分布曲线如图13 所示。

图13 桨叶质量分布Fig.13 Blade mass distribution
桨叶带配重挥舞、摆振和扭转振型如图14~图16 所示,由于配重位置位于1 990~2 090 mm 之间,从图14~图16 可以看出:配重正处于挥舞二阶、四阶和摆振二阶波腹的位置,因此增加配重后,挥舞二阶、四阶和摆振二阶频率降低;扭转一阶振型近似为一条直线,说明有无配重对其固有频率影响较小。
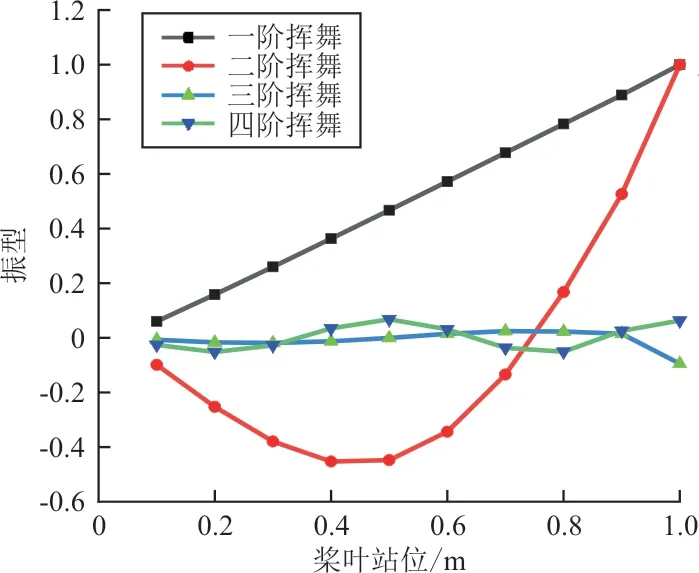
图14 挥舞前四阶振型图Fig.14 Top four mode shapes of flap

图15 摆振前二阶振型图Fig.15 Top two mode shapes of lag
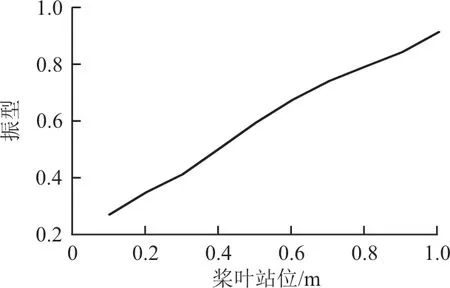
图16 扭转一阶振型Fig.16 The first mode shape of torsional
工作转速下桨叶固有频率如表1 所示,可以看出:该配重主要是为了调整挥舞四阶固有频率。
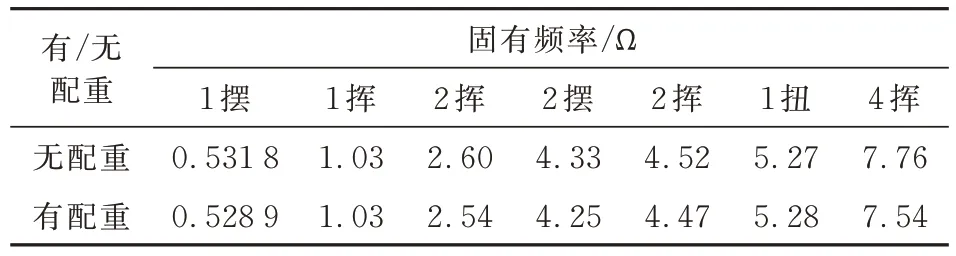
表1 工作转速下桨叶固有频率Table 1 Blade natural frequency at working speed
3 结论
(1)前掠角度对桨叶前三阶固有频率影响不大,第四阶和第五阶固有频率随着前掠角度的增大略微上升,第六阶和第七阶固有频率随着前掠角度的增大略微变小。
(2)后掠角度对桨叶前三阶固有频率影响不大,第四阶和第五阶固有频率随着后掠角度的增大而逐渐变小,第六阶和第七阶固有频率随着后掠角度的增大逐渐增大。
(3)桨叶配重主要是为了调整挥舞四阶固有频率,对桨叶其他频率影响较小。
