基于数值方法求解的周期加筋板声振特性研究

胡毅钧，王 伟，金叶青，叶梦熊

(1．海军装备部驻沈阳地区军事代表局，辽宁 沈阳110031;2．海军驻431 厂军事代表室，辽宁 葫芦岛，125004;3．武汉第二船舶设计研究所，湖北 武汉430064)

0 概 述

周期加筋板被广泛应用于舰船、飞机、高速列车等外壳结构中。当外壳结构受到外部激励时，会向外部或内部流场中辐射噪声，降低船舶的隐声性和飞机、高速列车的舒适度。因此，开展周期加筋板的声振特性研究，对于增强隐蔽性和提高舒适度具有重要意义。

针对周期加筋板在外部激励下的动态响应和声学特性，在过去的半个多世纪里已经提出了不同理论模型［1－10］。其中，Lee 和Kim［3］应用空间谐波展开法研究了无限大单向周期加筋板的声透射问题，在他们的研究中加强筋被等效为弹簧和扭簧的组合模型。Mace［4－5］运用傅里叶变换法求解了流体载荷作用下单向周期加筋板在任意点激励或线激励下的声辐射问题，但是只考虑加强筋弯曲运动的影响。Maxit［6］运用离散傅里叶变换法并考虑加强筋弯曲和扭转运动的影响，建立理论模型研究了单向周期加筋板在波数域和空间域中响应，但是求解过程太过繁琐，不便于数值编程操作。金叶青等［9］通过综合Mace 和Maxit［5－6］方法的优点，建立了一种计算水中周期加筋板在简谐点力作用下的远场辐射声压的高效方法，通过与文献［6］的计算结果对比验证了其方法的有效性，并且借助该方法研究激励力位置，板厚，加强筋间距和尺寸对周期加筋板声辐射特性的影响。

本文将在文献［9］所给出的周期加筋板声振耦合方程解析表达式的基础上，给出更加详细的数值求解方法，以此来研究周期加筋板的远场声辐射特性及波数域中的振动特性。

1 理论模型

考虑如图1 所示的无限大流体负载周期加筋板，y 方向上有一系列平行排列的加强筋沿着x 方向等间距均匀分布，加强筋间距为L。当从平板下侧施加一单位简谐点力于平板或加强筋上时，会使得加筋结构产生振动继而向平板上侧的流场中辐射声压，反过来声压也会影响加筋结构的运动。其中，机械点力作用点的位置为x0，其中x0∈［0，L］。

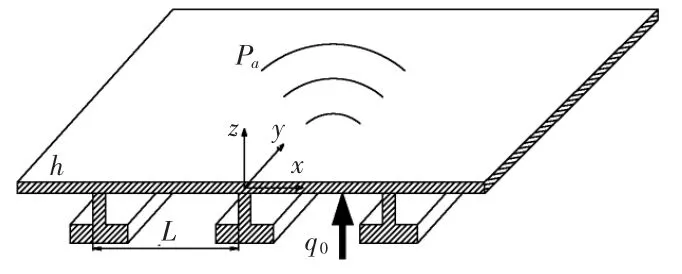
图1 机械点力作用下平行加筋板声辐射示意图Fig.1 Sketch of sound radiation of periodically stiffened plate under concentrated force

为研究周期加筋板的声振特性，文献［9］基于经典薄板理论，通过充分考虑加强筋的弯曲和扭转运动，并借助傅里叶变换法在波数域中求解周期加筋板的声振耦合方程，给出机械点力作用下周期加筋板声振理论耦合方程的解析表达式如下:

其中，αm=α +2πm/L，(m = n = － ∞ ～+ ∞)。

方程(1)中各种参数的含义详见文献［9］。

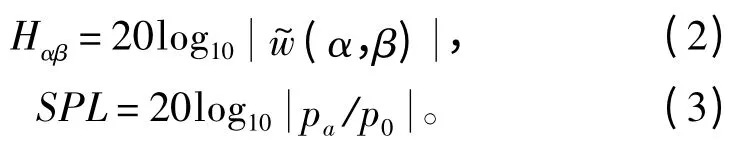
式中:pa的具体表达式可由文献［9］得到;p0= 1E －6 Pa 为水中的参考声压。

本文将首先给出方程(1)的一种数值求解方法，在此基础上再研究周期加筋板的远场声辐射特性和波数域中的振动特性。

方程(1)左右两边同时除以Z(αm，β)，可得:

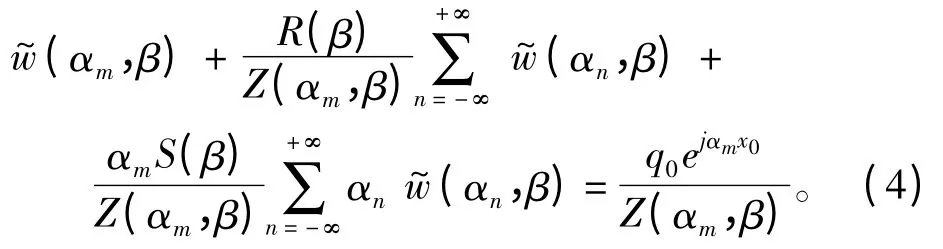
定义下式:

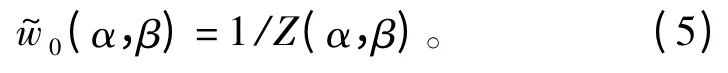
利用方程(5)可将方程(4)简化如下:

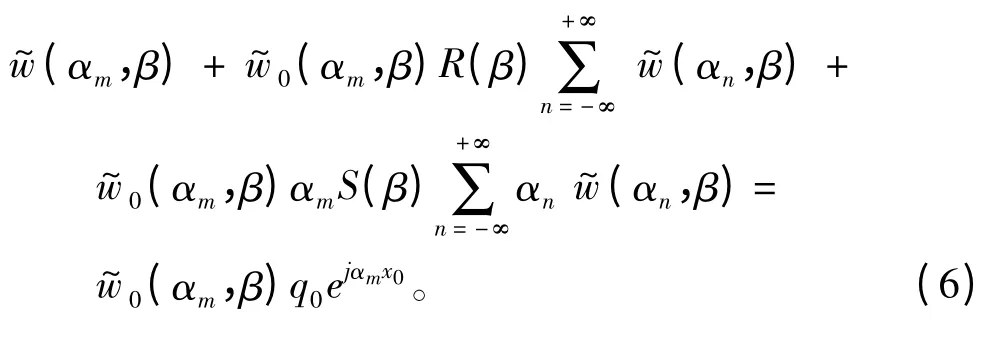
2 数值截断方法

限于本文篇幅的约束及为了达到演示的目的，本文令m =2，则m = －2，－1，0，1，2，这样将会得到关于未知数(α－2，β)，(α－1，β)，(α0，β)，(α1，β)和(α2，β)的5 个方程。其中，α－2=α + 2π(－ 2)/L，α－1= α + 2π(－ 1)/L，α0= α +2π(0)/L，α1=α+2π(1)/L，α2=α+2π(2)/L。将其代入到方程(6)中，则可以得到用于计算周期加筋板在波数域中横向位移的矩阵方程如下:

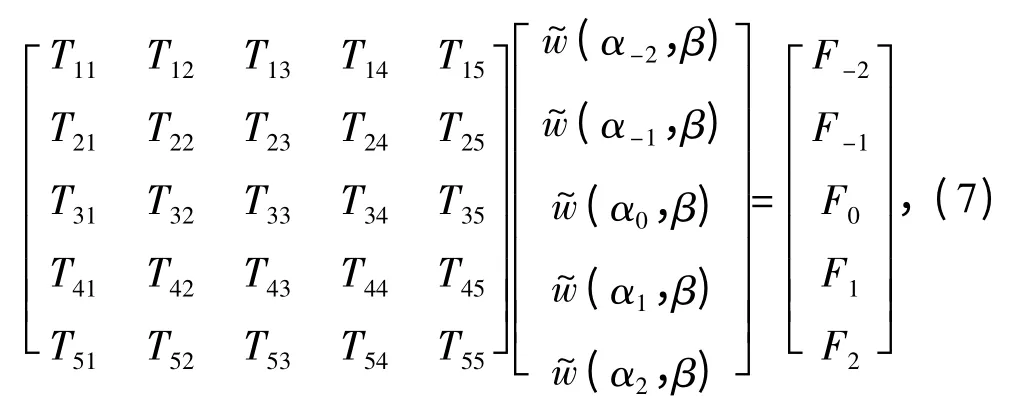
其中，矩阵方程中的各项系数如下:

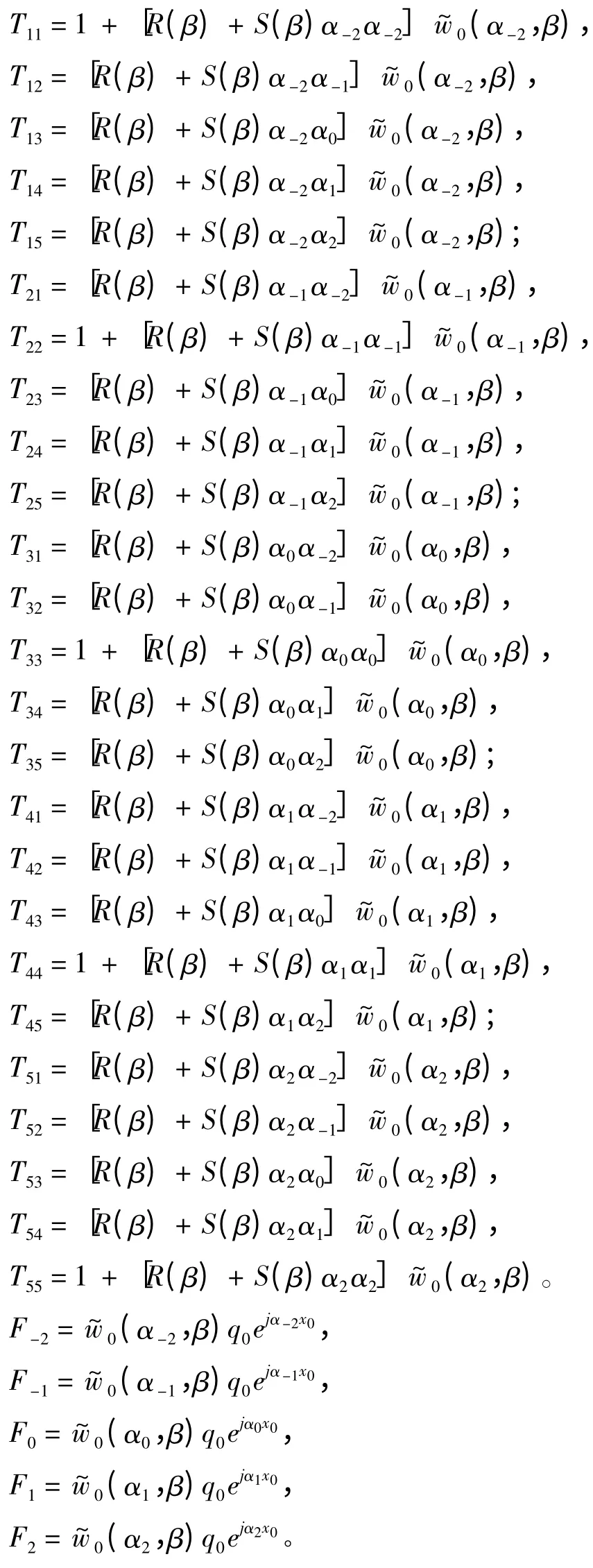
3 数值结果与讨论

本节将利用式(2)和式(3)来计算点激励作用下，系统参数对周期加筋板声振特性的影响规律。本文将通过使用复弹性刚度E (1 + jη)来计及板和加强筋结构阻尼的影响，其中η 为结构的损耗因子，令η =0.02。

数值计算中，假设平板上半空间流体为水，其密度ρ0=1 000 kg/m3，水中声速c0=1 500 m/s;机械点力的幅值q0=1N，作用点位置为(x0，0)，其值可取(0，0)，(L/4，0)， (L/3，0)和(L/2，0);球坐标中的声场点Q 的坐标为r =50m，θ =45°，φ =45°。最后将得到的远场辐射声压级都换算成r = 1 m 处的声源级;设平板和加强筋材料为钢;计算横向位移谱(Hαβ)，加强筋的横截面定为T型截面，其参数为A = 0.024 m2，Ix= 1.10 E －4 m4，Io=5.60 E －4 m4，J =3.60 E －5 m4;计算远场辐射声压级(SPL)，加强筋的横截面定为矩形截面，其参数为A =4.94 E －4 m2，Ix=5.94 E －8 m4，Io=6.64 E－8 m4，J=2.18 E－8 m4。

3.1 加强筋作用的影响

为了研究周期加筋板波数中的横向位移谱，先对比分析无限大平板和无限大周期加筋板的横向位移谱图，如图2(a)和图2(b)所示。数值计算时，平板厚度h=0.048 m，加强筋间距L =1.2 m，作用点x0=L/4，频率f=1 000 Hz，计算无限大平板的横向位移谱时，令周期加筋板的截面参数取无限小值。

由图2(a)可知，无限大光滑平板的横向位移谱中存在2 个半径不同的圆。其中，小细圆被称为流体“声波圆”。小圆的半径R1= ω/c0=4.19 m－1，表示为流体介质中的声波波数k0。大粗圆被称为平板“弯曲波圆”，其半径R2=9.76 m－1，表示为流体介质中无阻尼平板的弯曲波波数，其值的大小可以通过迭代方法求解其频散方程(8)近似计算得到。当时，流场中的平面波为耗散波，此时光滑平板的振动位移呈指数衰减，辐射声能呈现近场特性。当波数处于这个区域时，平面波为传播波。这部分声波可以辐射到远场，因此在声辐射中起主导作用。

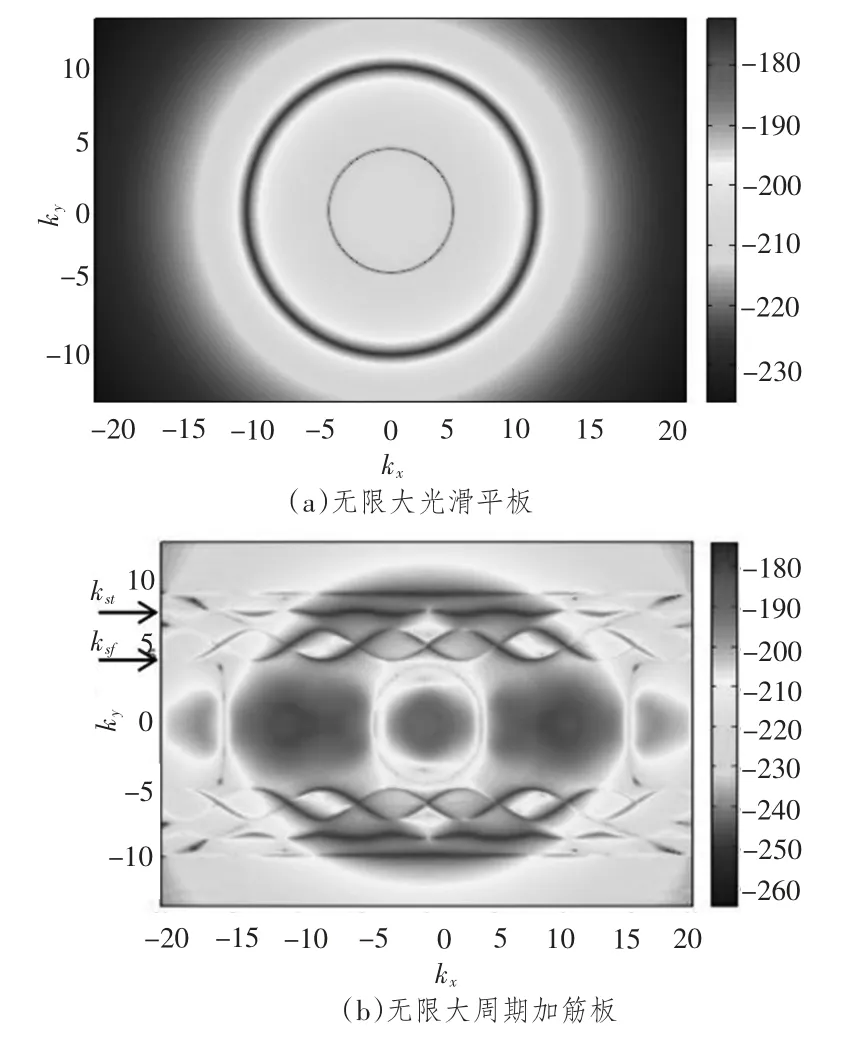
图2 无限大平板和周期加筋板Hαβ 的对比Fig.2 Hαβ of infinite smooth plate and periodically stiffened plate

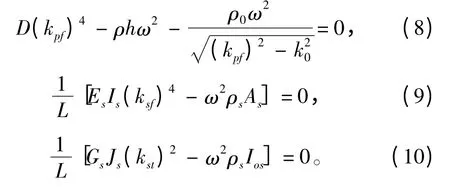
对比图2(a)和图2(b)可知，图2(b)中除了包含与图2(a)中相同的“声波圆”与平板“弯曲波圆”以外，同时还包含两部分对称于ky轴的“振荡区”。这部分是由于平板的横向弯曲运动与加强筋横向弯曲及扭转运动之间相互作用而产生的，其值大小分别为4.23 m－1和7.70 m－1。它们分别表示加强筋的弯曲波波数ksf和扭转波波数kst，可以分别由加强筋的横向弯曲运动和扭转运动的频散方程(9)和(10)计算得到。

3.2 加强筋间距的影响

本节将研究不断改变加强筋间距对周期加筋板横向位移谱和远场辐射声压的影响规律，如图3 和图4所示。计算Hαβ时，平板厚度h=0.048 m，加强筋间距L=0.8，1.0，1.2，1.5 m，作用点x0=L/4，频率f =1 000 Hz;计算SPL 时，平板厚度h=0.005 m，加强筋间距L =0.15，0.2，0.25 m，作用点x0=0，L/4，L/3，L/2，频率f=100 ～1 000 Hz。

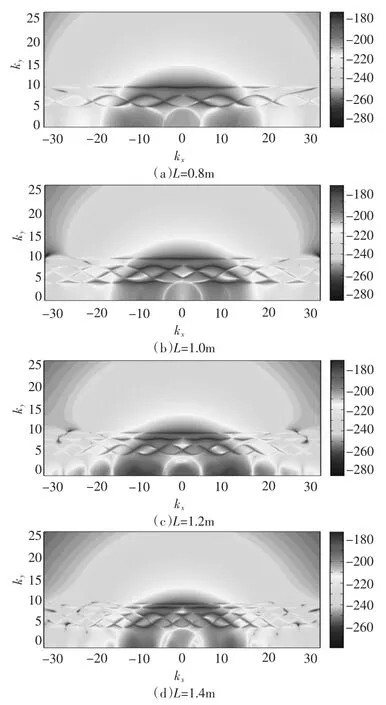
图3 不同加强筋间距下平行加筋板的Hαβ 图Fig.3 Hαβ of periodically stiffened plate in different spacing of the stiffeners

由图3 可知，改变加强筋间距对结构横向位移谱的影响比较明显。随着加强筋间距不断增大，横向位移谱中平板“弯曲波圆”附近的光亮区域逐渐缩小，并向“弯曲波圆”逐渐靠近，值的大小也逐渐减小，结构的辐射能力逐渐在下降。同时，随着加强筋间距不断增加，螺旋线的波动周期也逐渐变得密集。这说明随着平板厚度不改变的情况下，随着加强筋间距不断增加，平板与加强筋之间的耦合效应越来越弱，最终加筋板的振动特性将渐趋于光滑平板。

由图4 可知，3 条SPL 曲线总体上的变化趋势还是能保持很好的一致性。在低频段，改变加强筋间距对结构声辐射的影响不大，3 种不同强筋间距时的SPL 曲线基本上是重合的;加强筋间距变化主要在中高频段显著影响结构的声辐射，这是因为此时平板弯曲波波长与结构加强筋间距在量值上相当。随着加强筋间距不断增加，结构SPL 曲线上的波峰和波谷不断向低频方向移动。这是因为结构的固有频率随着加强筋间距不断增加而减少，因而SPL 曲线上与结构固有频率所对应的波峰和波谷才会逐渐向低频推移。因此，通过合理选择加强筋间距可以设计出力学和声学性能最优的结构形式。

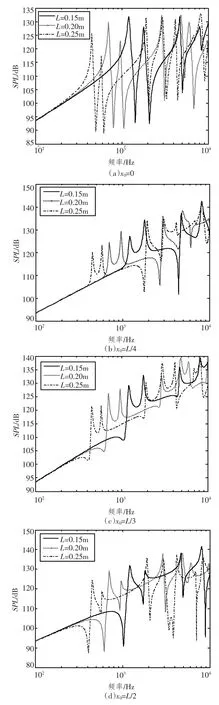
图4 不同加强筋间距下平行加筋板的SPL 曲线Fig.4 SPL curves of periodically stiffened plate in different spacing of the stiffeners

4 结 语

为了研究周期加筋板远场声辐射特性和波数域中的振动特性，本文在文献［9］的基础上，首先给出一种数值求解方法，然后在此基础上对比分析了无限大平板和周期加筋板在波数域中的横向位移谱，最后分析了加强筋间距对周期加筋板横向位移谱和远场辐射声压的影响。主要结论如下:

1)周期加筋板的横向位移谱中存在3 个特征区域，即“声波圆”、“弯曲波圆”和耦合“振荡区”。

2)改变加强筋间距影响非常明显。随着加强筋间距不断增加，平板与加强筋之间的耦合效应越来越弱，最终加筋板的振动特性将会渐趋于光滑平板。

3)随着加强筋间距不断增加会使得结构的固有频率降低，使得结构的SPL 曲线会向低频段偏移，而低频平滑段减少。

［1］MEAD D J，PUJARA K K．Space-harmonic analysis of periodically supported beams:response to convected random loading［J］．Journal of Sound and Vibration，1971，14 (4):525 －541．

［2］辛锋先，卢天健，陈常青．轻质金属三明治板的隔声性能研究［J］．声学学报，2008，33(4):340 －347．

［3］LEE J H，KIM J． Analysis of sound transmission through periodically stiffened panels by pace harmonic expansion method［J］．Journal of Sound and Vibration，2002，251(2):349－366．

［4］MACE B R．Periodically stiffened fluid-loaded plates．Ⅰ:Response to convected harmonic pressure and free wave propagation［J］．Journal of Sound and Vibration，1980，73(4):473－486．

［5］MACE B R． Periodically stiffened fluid-loaded plates． Ⅱ:Response to line and point forces［J］．Journal of Sound and Vibration，1980，73(4):487 －504．

［6］MAXIT L．Wavenumber space and physical space response of a periodically ribbed plate to a point drive:A discrete approach［J］．Applied Acoustics，2009，70(4):563 －578．

［7］金叶青，庞福振，姚熊亮，等．正交加筋板声透射的板梁理论模型研究［J］．声学学报，2012，37(6):610 －620．

［8］金叶青，庞福振，姚熊亮，等．基于板梁组合理论的正交加筋板声振特性分析［J］．振动工程学报，2012，25(5):579 －588．

［9］金叶青，庞福振，姚熊亮，等．一种分析周期加筋板声辐射的高效方法［J］．声学学报，2013，38(3):338 －345．

［10］金叶青，姚熊亮，庞福振，等．均匀流中剪切变形加筋层合板声与振动特性研究［J］． 物理学报，2013，62(13):13430601 －13430613．