压缩域直扩测控通信信号伪码跟踪方法研究

程艳合 杨文革



压缩域直扩测控通信信号伪码跟踪方法研究

程艳合*杨文革

(解放军装备学院光电装备系 北京 101416)

压缩感知理论已经在测控(TT&C)通信相关领域有初步应用尝试，能够有效降低采样率和数据率，但同时其重构算法复杂度偏高、计算资源消耗过大，这与系统的实时性要求之间存在矛盾。论文基于直扩测控(DS TT&C)通信信号稀疏性，对传统伪码跟踪环进行改进，提出一种基于随机解调压缩采样的压缩域伪码跟踪环。该环路不再需要进行信号重构处理，能够直接从直扩测控通信信号的压缩采样值中提取伪码(PN)延时相位信息。该文首先深入分析所提出环路模型及其鉴别特性，其次通过研究交叉噪声特性，对跟踪精度进行理论分析。分析和仿真结果表明，所提出环路能够在压缩域实现伪码延时相位跟踪。该环路可以应用在基于压缩感知的直扩、混扩信号处理等相关领域，具有一定工程应用价值。

伪码跟踪；压缩感知；跟踪精度；载波辅助；野值剔除

1 引言

扩频体制具有隐蔽性、抗干扰、抗截获等优点，因此受到了测控通信领域的广泛重视，基于扩频方式统一测控通信系统已经实现工程化。虽然现行扩频测控系统具备一定的电子对抗能力，但在日趋复杂的空间信息对抗环境下，依然面临着严重安全威胁，表现出信息保密性能和抗干扰能力的不足。针对该问题，学者们提出了一些方法，比如提高测控频段、扩频码速率和混合扩频技术等，它们会不同程度增大系统带宽[1]。然而，带宽的增大会给接收机前端A/D提出更高要求，致使系统按照Nyqiust定律进行采样变得十分困难[2]。另一方面，即使系统能够以Nyqiust速率进行采样，带宽增大意味着数据率提高，系统将面临高数据率问题，给后续传输、记录存储、捕获跟踪和解调处理带来沉重负担。

压缩感知是一种全新信息获取理论，在该理论框架下，采样率不再取决于信号带宽，而是由信号信息量决定，这为降低信号采集成本和缓解解调处理压力提供一个崭新的思路[3]，目前在相关方面已经取得一些成果。文献[4]根据GPS信号相关稀疏性，提出一种新型信号捕获方法，可减少相关器数量。文献[5]针对扩频信号，提出了一种基于压缩感知信号采集和恢复方法，但未考虑载波和噪声等因素。文献[6]通过构造稀疏基字典对直扩信号进行了稀疏性分析。这些成果都不可避免要进行信号重构，而重构算法复杂度偏高，需要大量的计算资源消耗[7]。测控通信系统的处理目标是信号流，其计算复杂度和实时性是首要考虑因素。因此，传统压缩感知重构算法并不适用于大多数的实时处理系统。

在测控通信系统中，伪码跟踪是保持码同步基础，跟踪精度直接关系系统测距性能，因此码跟踪环一直是接收机设计的核心环节[1]。本文提出了一种新型压缩域伪码跟踪环，该环路可以直接从扩频信号压缩采样值中提取伪码延时相位信息，不再需要进行信号重构，在计算复杂度方面具有很强的优势。

2 非相干型压缩域伪码跟踪环

2.1环路模型

测控通信系统一般采用非相干延时锁定环，其伪码相位估计实质是通过计算输入信号与本地再生信号加权内积来实现[1]。依据压缩域信号估计理论，两稀疏信号内积在一定误差范围内可由其压缩采样值内积运算等效替代[8]，结合直扩信号稀疏性[6]，本文提出一种非相干型压缩域伪码跟踪环，如图1所示。该环路由压缩采样器(由表示)、延时锁定鉴别器、环路滤波器、码NCO与扩频码发生器等组成。扩频码发生器产生超前、即时、滞后再生伪码，并与再生同相、正交载波分别相关生成本地参考信号，压缩采样器实现对输入信号和本地参考信号压缩处理，输出分别进行相关和积分清零，并对积分结果进行误差鉴别，鉴别结果通过环路滤波器对码NCO与扩频码发生器进行调节，完成对伪码的跟踪。同时，可由载波跟踪环输出来实时调整码NCO输出频率，消除目标运动引入的码多普勒动态。

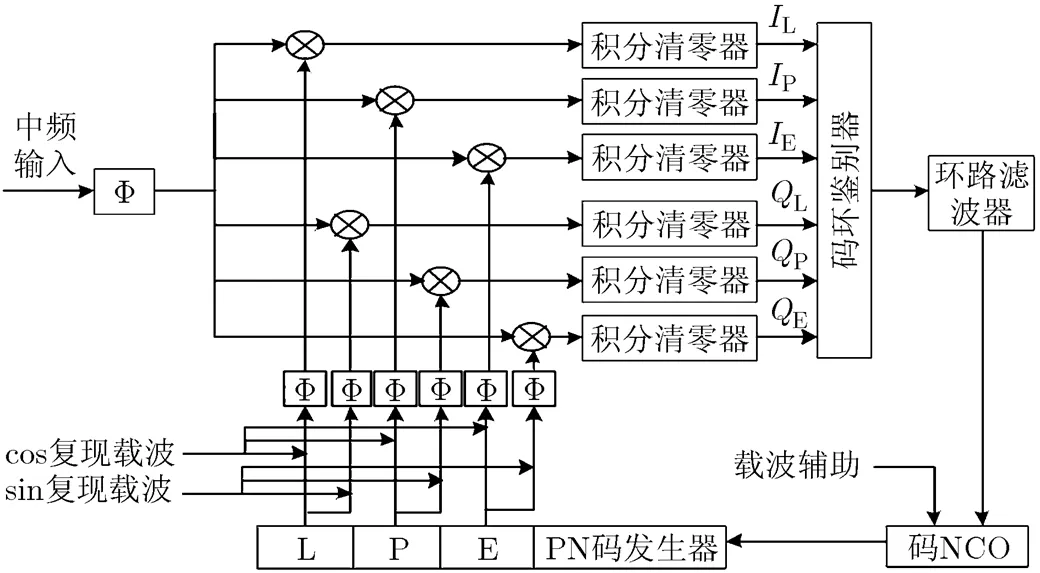
图1 压缩域伪码跟踪环的结构框图

码跟踪环路具有实时性要求，给压缩采样器设计提出一些约束条件，主要是因果性、低延迟和低复杂度。随机解调压缩采样器满足上述约束条件，且易于实现，因此采用该类型压缩采样器。注意，环路中压缩采样器需输入相同伪随机序列，保持积分器脉冲响应一致，并保证低速采样同步[12]。

2.2环路分析

设输入信号是信息调制直扩信号，可表示为[1]

I路乘法器输出为

其中

假设伪码周期与数据位相参，积分清零周期与伪码周期同步，则在一个积分清零周期内数据位不会产生翻转。同时，假设载波与伪码相位对积分清零的影响相互独立，根据三角函数累加算式可得

同理，可得其他超前、即时和滞后支路积分为

非相干型鉴别器常见的有超前减滞后功率鉴别器和点积功率鉴相器[1]，本文主要采用点积功率鉴别器，则本文所提出环路的鉴别器输出可表示为

3 压缩域环路跟踪精度分析

3.1交叉噪声特性分析

相对于传统码跟踪环，压缩域环路额外引入了一个交叉噪声项。不失一般性，选取I路即时支路对交叉噪声特性展开分析。假设压缩采样器抽头系数和扩频码都是零均值伪随机序列，加性噪声为零均值高斯随机变量，三者相互独立，则根据式(6)，忽略输入信号噪声，可得其均值为

根据方差定义，可得交叉噪声的方差为

同理，易得其他支路引入交叉噪声也都是零均值白噪声，且方差与式(19)相同，和压缩比成正比。

综上分析可知，与传统环路相比，压缩域环路会引入额外零均值白噪声，等效于引入一个信噪比恶化量。假设输入载噪比，双边带带宽，有，已知输入噪声与引入噪声不相关，则等效总噪声方差为，等效信噪比为

3.2 跟踪精度分析

伪码环路跟踪精度影响因素主要包括输入信号动态应力和环路热噪声[13]。一般采用载波辅助来减弱乃至完全消除伪码多普勒动态，降低环路动态性要求[14]。载波辅助也适用于压缩域环，如图1所示。

在载波辅助条件下，跟踪误差源主要考虑热噪声，文献[1]和文献[14]给出了采用点积鉴别器非相干码跟踪环热噪声误差公式，结合式(19)和式(20)，对其改进可得压缩域码跟踪环热噪声引入跟踪误差为

4 码鉴别器野值剔除方法

压缩域环路同时存在热噪声和引入交叉噪声，在低信噪比或大压缩比情况下，鉴别器输出结果会随机出现异常极大值，即野值点。野值点会降低环路跟踪精度和稳定性。针对该问题，本文采用了码鉴别器野值剔除方法，如图2所示。

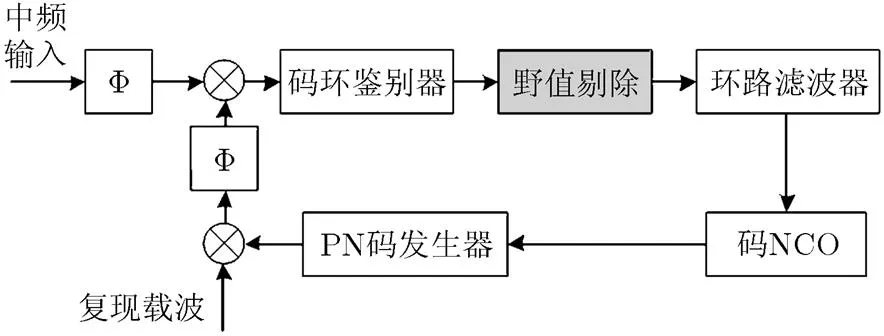
图2 压缩域伪码跟踪环野值剔除原理框图

5 仿真实验

本节对压缩域伪码跟踪环进行仿真分析，具体分为可行性验证、跟踪性能和野值剔除性能分析3部分。注意，仿真参数设置参照现役直扩测控系统，有利于与系统指标进行比对，但压缩域环路适用带宽不止于此，实际上带宽越宽其优势越明显。

实验1 环路可行性验证 伪码周期1023，伪码速率10.23 Mcps，载波中心70 MHz，采样率56 MHz，载噪比52 dBHz，初始相位差0.5 chip；阻尼系数0.707，环路带宽5 Hz，相关间隔1 chip，积分时间0.1 ms；压缩比取1, 10，结果如图3所示。注意，压缩比取1时压缩域环路退化成传统环路。

由图3可知，本文所提出环路能够锁定输入信号，且入锁时间与传统环路相同；两者锁定后稳定输出数据的方差分别为0.0061 chip和0.0029 chip，即压缩域环路跟踪精度略低于传统码环，这是由压缩采样引入噪声所致，是降低采样率所需付出代价。

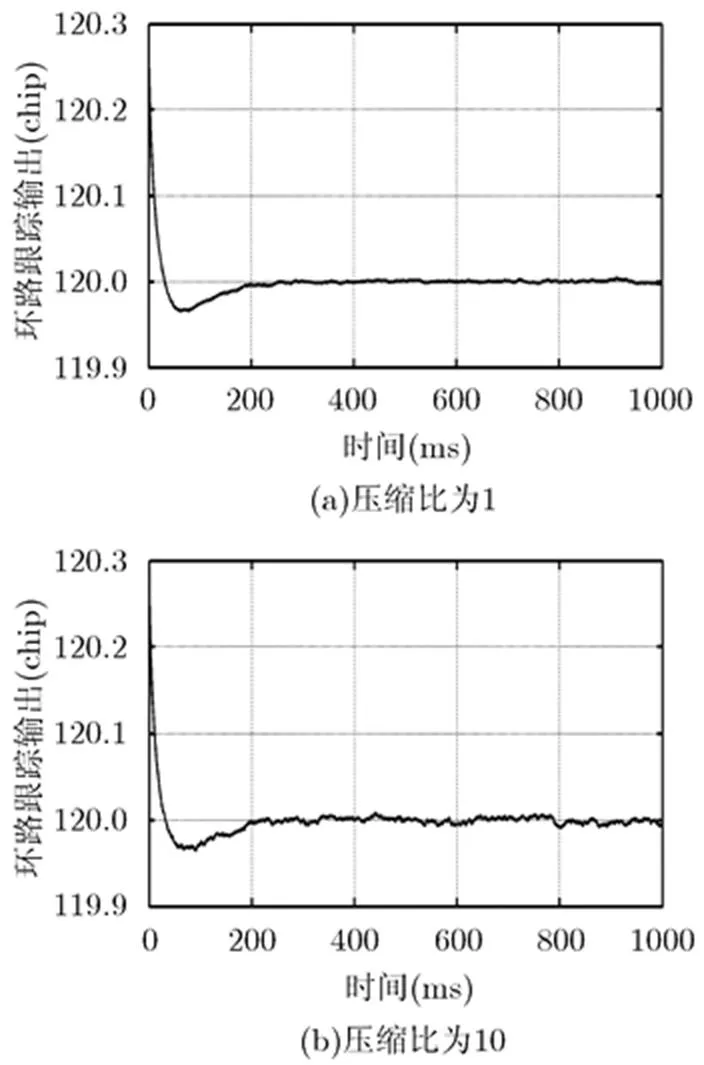
图3 压缩域伪码跟踪环的码跟踪结果

实验2 跟踪性能分析 考察信噪比、压缩比两方面，首先固定载噪比47 dBHz，压缩比取[1,700]；其次固定压缩比为1, 10和40，载噪比取[35,60] dBHz，其他参数与上节相同，结果如图4所示。

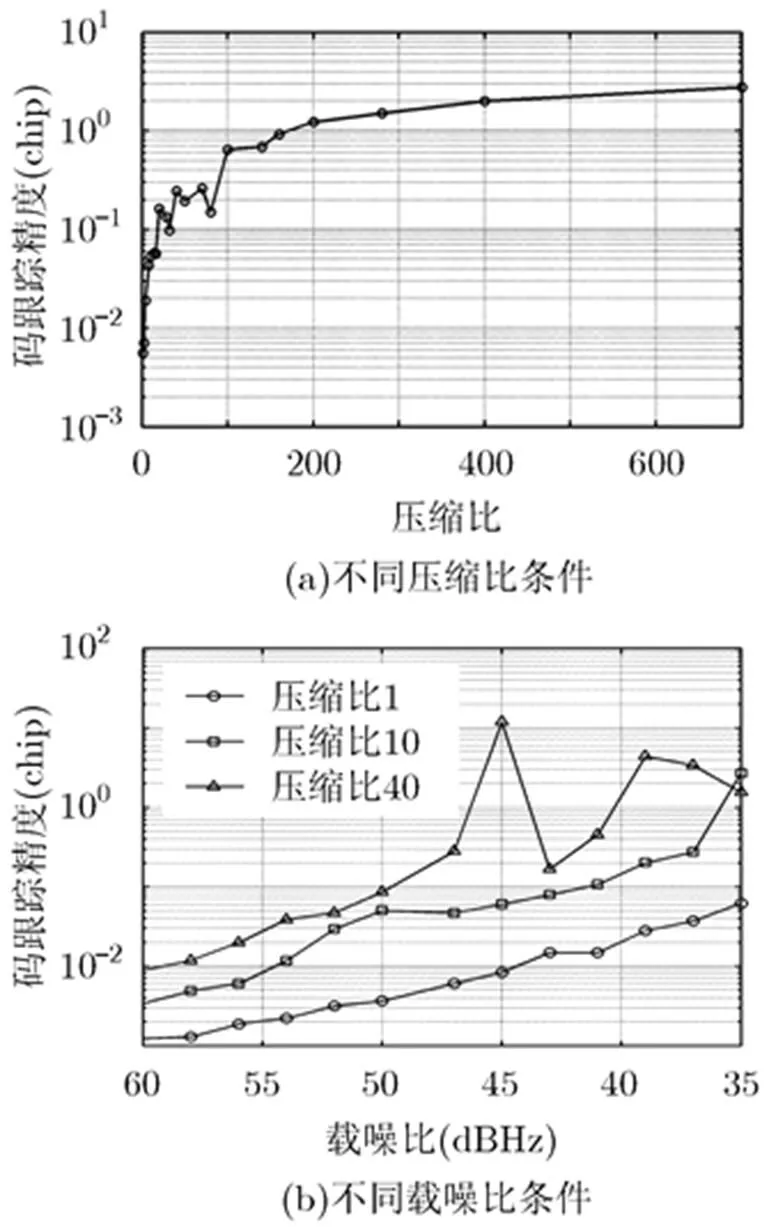
图4 压缩域伪码跟踪环跟踪精度变化规律

由图4可知，压缩域环路跟踪误差随压缩比增大，且高于传统环路，这是由压缩采样引入噪声所致；但只要压缩比不大于10，载噪比高于47 dBHz，跟踪精度可保持在0.05 chip以内，能够稳定跟踪伪码相位变化，跟踪精度满足测控通信系统测距要求。

实验3 野值剔除性能分析 假设捕获精度0.5 chip，环路带宽5 Hz，鉴别器增益2，由式(22)有判别门限5，其他参数与前文相同，结果如图5所示。

图5 野值剔除后环路跟踪精度变化规律

对比图4和图5可知，在传统跟踪环中，野值剔除效果不明显；在压缩域跟踪环中，野值剔除能够降低跟踪误差，且压缩比越高、载噪比越低，效果就越显著；在信噪比为47 dBHz，压缩比高达100时，环路仍能把码跟踪误差控制在0.1 chip以内，基本能够满足测控通信系统的测距要求。

6 结束语

针对压缩感知理论在测控通信中应用所面临的重构算法复杂度与系统实时性要求之间的矛盾，本文提出了一种新型压缩域伪码跟踪方法，并对压缩域环路及其跟踪精度进行了深入分析，提出了码鉴别器野值剔除方法。相对于先重构信号再利用传统环路跟踪的常规思路，压缩域伪码跟踪环不再需要重构原信号，在计算复杂度方面具有很强优势；与传统环路相比，压缩域环路能够降低信号采样率或数据率，并且通过野值剔除处理，跟踪精度能够满足测控通信系统测距要求。尽管本文以压缩域直扩测控通信信号伪码同步为研究背景，但研究成果不仅仅局限于此，可以扩展到DS/FH HSS信号压缩感知处理研究中。后续工作将致力于构建基于压缩域同步解调的扩频信号压缩感知接收处理框架。

参考文献

[1] 刘嘉兴. 飞行器测控与信息传输技术[M]. 北京: 国防工业出版社, 2011: 13-24.

Liu Jia-xing. Spacecraft TT&C and Information Transmission Technology[M]. Beijing: National Defense Industry Press, 2011: 13-24.

[2] Venosa E, Harris F J, and Palmieri F. Software Radio[M]. New York: Springer-Verlag Inc., 2012: 30-41.

[3] Kazunori H, Masaaki N, and Toshiyuki T. A user’s guide to compressed sensing for communications systems[J]., 2013, E96-B(3): 685-712.

[4] Li X, Rueetschi A, Eldar Y C,.. GPS signal acquisition via compressive multichannel sampling[J]., 2012, 5(2): 173-184.

[5] 安建平, 王帅. 基于压缩感知的直接序列扩频信号采集和恢复方法[P]. 中国专利, 102710568, 2012-10-03.

An Jian-ping and Wang Shuai. Direct sequence spread spectrum signal acquisition and recovery method based on compressive sensing[P]. Patent of China, 102710568, 2012-10-03.

[6] Cheng Y H, Yang W G, and Zhao J. Compressive sensing for DS TT&C signals based on basic dictionary building[C]. The 27th IEEE Conference of Spacecraft TT&C Technology in

China, Guangzhou, China, 2014: 211-221.

[7] Masood M and Al-Naffouri T Y. Sparse reconstruction using distribution agnostic bayesian matching pursuit[J]., 2013, 61(21): 5298-5309.

[8] Davenport M A, Boufounos P T, Wakin M B,.. Signal processing with compressive measurements[J]., 2010, 4(2): 445-459.

[9] Laska J, Kirolos S, Massoud Y,.. Random sampling for analog-to-information conversion of wideband signals[C]. IEEE Dallas Circuits and Systems Workshop on Design, Application， Integration and Software, Richardson, TX, USA, 2006: 119-122.

[10] Luo C E and Zhu L C. Jittered random sampling with a successive approximation ADC[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 2014: 1798-1802.

[11] Luo C and McClellan J. Discrete random sampling theory[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 2013: 5430-5434.

[12] Smaili S and Massoud Y. Accurate and efficient modeling of random demodulation based compressive sensing systems with a general filter[C]. International Symposium on Circuits and Systems, Melbourne, Australia, 2014: 2519-2522.

[13] Binti Mokhtar S M A and Abdullah W F H. Memristor applied in delay locked loop for high lock speed and wide frequency range[C]. IEEE International Conference onSemiconductor Electronics, Kuala Lumpur, Malaysia, 2014: 350-353.

[14] 王永庆, 高磊, 吴嗣亮. 航天器扩频测控应答机伪码跟踪环技术[J]. 北京邮电大学学报, 2010, 33(4): 49-53.

Wang Yong-qing, Gao Lei, and Wu Si-liang. Design of code tracking loop for spacecraft TT&C transponder[J]., 2010, 33(4): 49-53.

[15] 王永庆, 乔媛, 吴嗣亮. 数字伪码跟踪环路中的野值剔除新方法[J]. 北京理工大学学报, 2009, 29(11): 998-1000.

Wang Yong-qing, Qiao Yuan, and Wu Si-liang. A new method of wild value elimination for digital code tracking loop[J]., 2009, 29(11): 998-1000.

Study on Pseudo-noise Code Tracking Method for Compressive Domain Direct Sequence Tracking Telemetry and Command Communication Signals

Cheng Yan-he Yang Wen-ge

(,,101416,)

Compressive sensing has a preliminary application to the field of Tracking, Telemetry, and Command (TT&C) and communication, which can effectively decrease sampling and data rate, but there is a contradiction between the real-time requirement and the computationally expensive recovery algorithm. In this paper, based on the sparsity of Direct Sequence (DS) TT&C and communication signals, a compressive domain Pseudo-Noise(PN) code tracking loop based on random demodulation compressive sampler is proposed. The loop can directly extract the code phase from compressive signal samples, which does not need to recover original signal. Firstly, the loop model and its identification characteristics are analyzed. Secondly, through research on cross noise, tracking accuracy is analyzed. Theoretical analysis and simulation results show that the proposed loop can track PN code phase in compressive domain. The loop may have an important application value to the field of DS Spread Spectrum (SS) and DS/Frequency Hopping (FH) Hybrid SS (HSS) signal processing based on compressive sensing.

Pseudo-Noise (PN) code tracking; Compressive sensing; Tracking accuracy; Carrier auxiliary; Outliers eliminating

TN92

A

1009-5896(2015)08-2028-05

10.11999/JEIT141654

程艳合 cheng20130810@foxmail.com

2014-12-29收到，2015-03-30改回，2015-06-09网络优先出版

程艳合： 男，1987年生，博士生，研究方向为航天测控技术、扩频信号处理、压缩感知理论及其应用.

杨文革： 男，1966年生，教授，博士生导师，研究方向为空间飞行器测控与通信系统、航天测控技术、压缩感知理论.