卫星导航信号无模糊抗多径码相关参考波形设计技术*
2019-07-29徐成涛谢郁辰
徐成涛,刘 哲,谢郁辰
(1. 国防科技大学 系统工程学院, 湖南 长沙 410073; 2. 国防科技大学 电子科学学院, 湖南 长沙 410073)
二进制偏移副载波(Binary Offset Carrier, BOC)信号是下一代卫星导航系统中广泛采用的新型调制信号,有助于实现军民用频谱分离和测距精度提升[1]。在L1频点,北斗、GPS、Galileo等全球卫星导航系统已将BOC(1,1)信号作为实现系统间互操作的基线信号。高阶BOC信号,如BOC(10,5)、BOC(15,2.5)和BOC(14,2)信号,被用于Galileo的公共安全管理服务、北斗和GPS的军用服务[2]。
BOC信号可视为二进制相移键控(Binary Phase Shift Keying,BPSK)信号和一个方波副载波的乘积,一般用BOC(m,n)表示,即信号扩频码码率fc=mf0,副载波频率fsc=nf0,基准频率f0=1.023 MHz。卫星导航系统的现代化BOC信号在提升系统定位导航授时(Positioning Navigation Timing,PNT)服务性能的同时,也给新体制信号的接收带来了挑战。
BOC信号的自相关函数不再是传统BPSK或四进制相移键控(Quadrature Phase Shift Keying,QPSK)信号的三角峰,而是在主峰旁边增加了多个逐渐下降的副峰。采用传统方法接收BOC信号,在伪码鉴别函数曲线上出现多个过零点,导致本地信号可能稳定跟踪在错误的位置而无法正确同步,产生的测距偏差可达几十米甚至上百米,称之为错锁或误锁问题[3]。
由于时、空域上的弱相关性,多径误差是目前卫星导航高精度定位、测距接收机误差的主要来源[4]。BOC类信号的多径抑制处理,在传统问题基础上,增加了去除跟踪模糊度的要求。此外,其他更复杂的复合BOC(Composite BOC,CBOC)、时分复用BOC(Time Multiplexed BOC,TMBOC)、交替BOC(Alternate BOC,AltBOC)等信号特性相差较大,其抗多径技术要求更高,且各具特色,对接收机内部的统一设计提出了挑战[5]。
伪码延迟锁定环(Delay Lock Loop,DLL)抗多径技术依托于传统DLL跟踪结构,硬件资源占用少,易于被接收机采用。主要包括窄相关技术、四相关器(Double-Delta)技术和码相关参考波形(Code Correlation Reference Waveform,CCRW)技术[6-7]。其中,窄相关和Double-Delta技术利用一组或两组不同间隔的超前滞后码线性组合构造码鉴别器。CCRW技术采用专门设计的闸波信号代替本地码,通过改变鉴相函数获得更优的多径抑制性能。窄相关与Double-Delta技术也可归于CCRW技术范畴。
卫星导航接收机广泛采用DLL结构接收信号,通过本地生成的信号和接收到的卫星信号进行相关运算,实现伪码同步跟踪,因此相关运算生成的鉴别曲线形状决定了跟踪算法的性能[8]。文献[9]提出了一种对鉴别曲线人为赋形并求解本地多相关器组合的方法,并给出了BOC(1,1)信号的仿真结果,但未考虑带限情况。文献[10]提出用类似最小二乘方法,采用两组相关器组实现BOC信号的非相干鉴别器曲线,但该方法将增大1倍的硬件资源并降低测距精度[11]。
本文对DLL中BOC信号鉴别曲线无模糊和抗多径特性精确赋形的方法进行研究,提出基于DLL最优鉴别曲线的GNSS信号码参考波形设计技术,给出最优鉴别曲线定义,采用最小二乘方法逆向求解本地参考波形,并解决带限情况下的病态矩阵问题。
1 最优鉴别曲线
卫星导航接收机的本地码相干鉴别器可以表示为扩频码的线性组合:
(1)
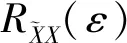
DLL多径抑制算法的基本原理是减小多径延迟信号在鉴别器内产生的误差,抑制多径信号对稳定点的影响。传统理论上最优鉴别曲线的定义如图1所示。
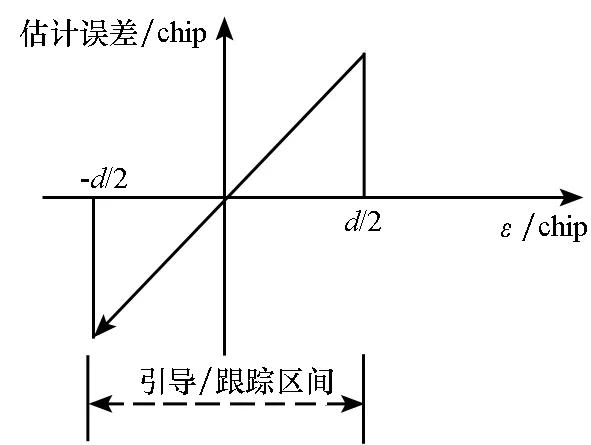
图1 传统最佳鉴别曲线Fig.1 Traditional best S-curve
传统意义上的最佳鉴别曲线的线性相应区域为[-d/2,d/2],跟踪误差在此区域内可实现引导和同步跟踪,跟踪误差在其他范围的鉴别输出为0。由于多径信号总是延迟于真实信号到达接收机,多径误差主要由鉴别曲线ε<0的部分决定,因此只有ε<0部分会影响多径误差,通过约束这部分鉴别曲线形状,即可保证鉴别曲线的抗多径性能最佳,如图2所示。
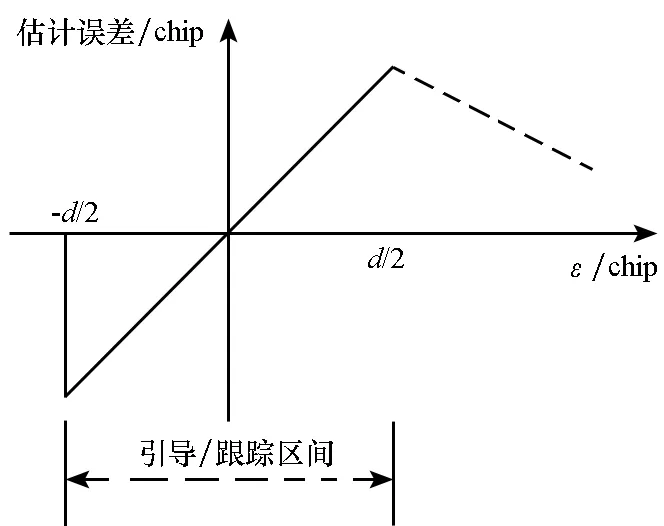
图2 抗多径最佳鉴别曲线Fig.2 Best S-curve for multipath mitigation
上述鉴别曲线对跟踪模糊度未做要求,为保证BOC信号跟踪只有一个稳定点,要求鉴别曲线在ε>0时不存在过零点。故最佳抗多径鉴别曲线应至少具有以下几个特征:
1)无系统性跟踪偏差,当准确跟踪时鉴别器应只受噪声影响,即D(0)=0;
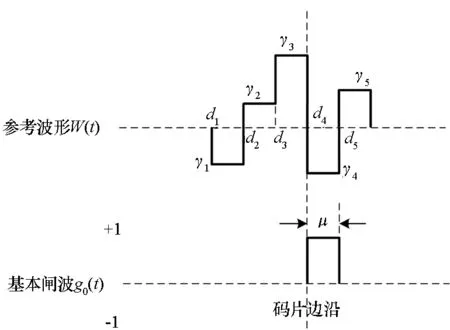
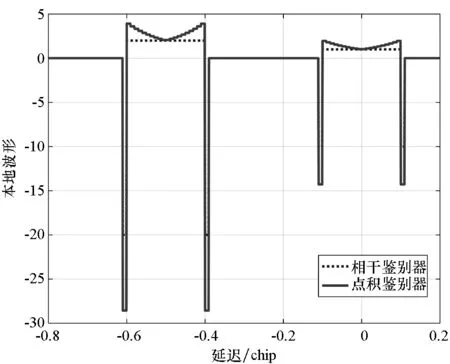
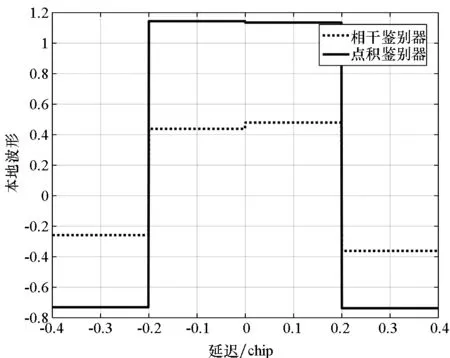
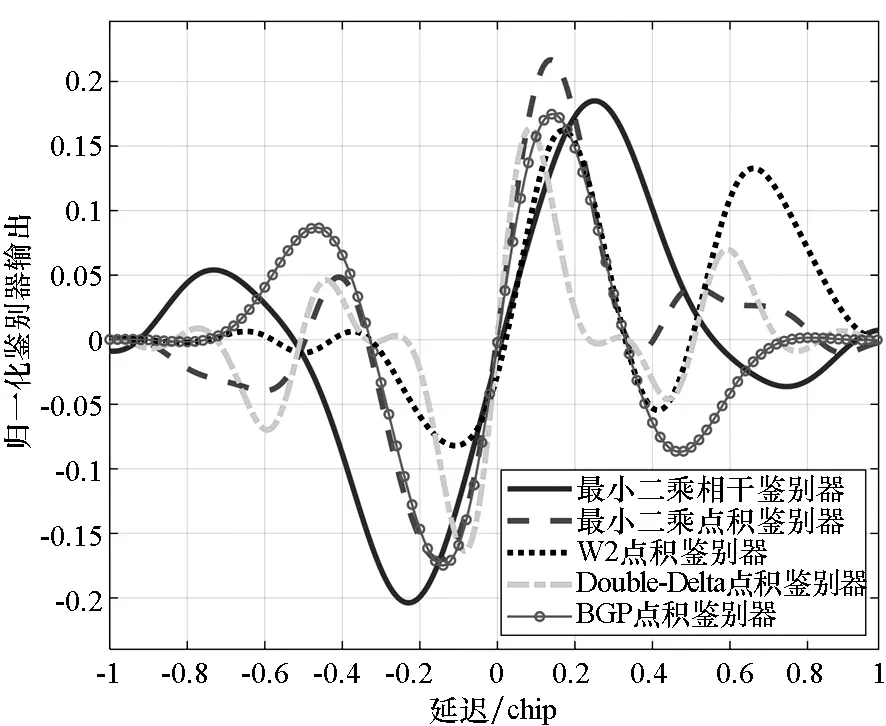
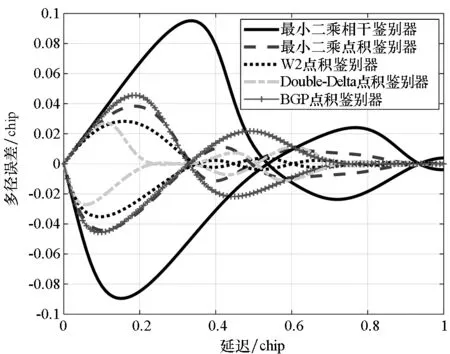
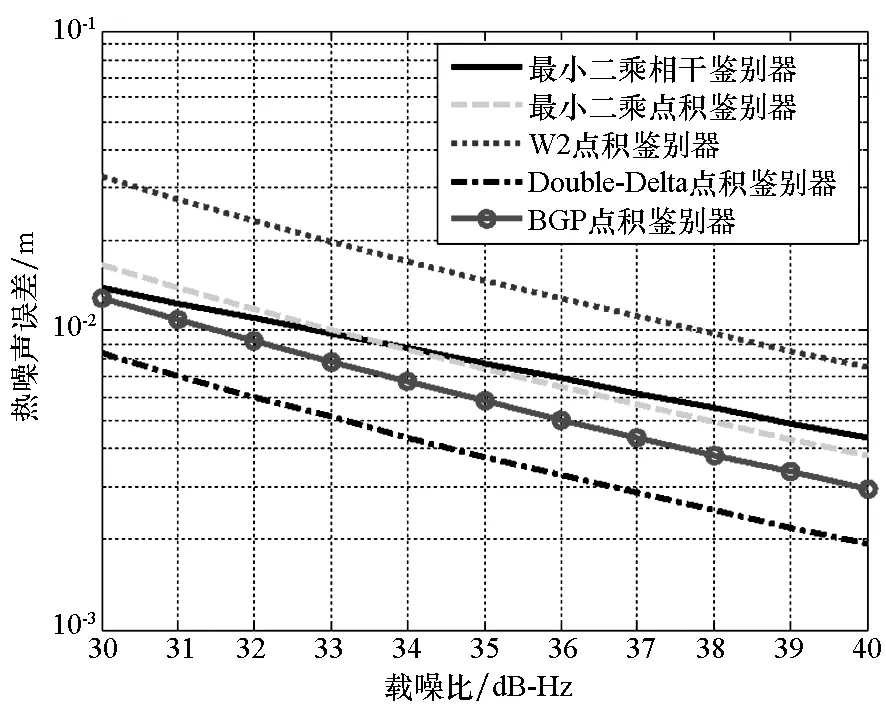
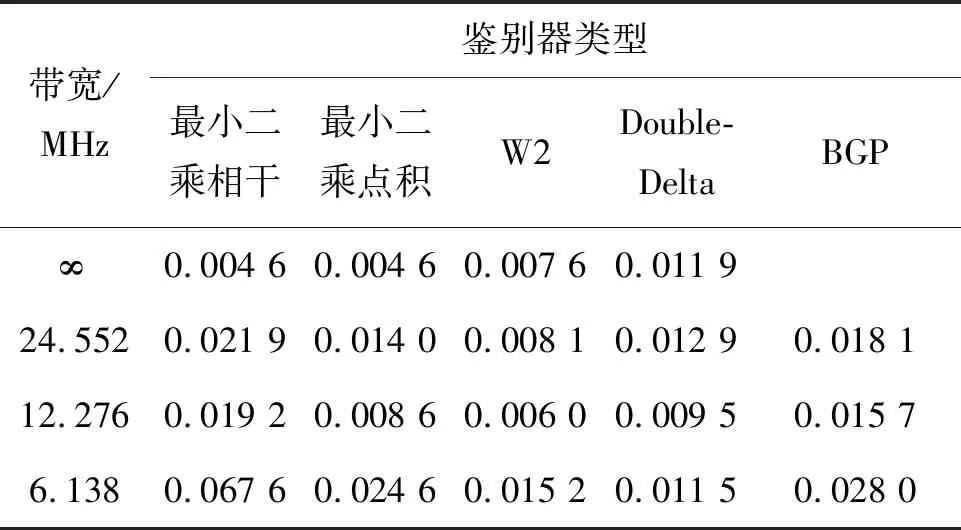
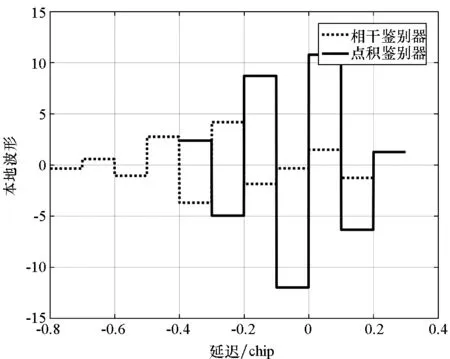
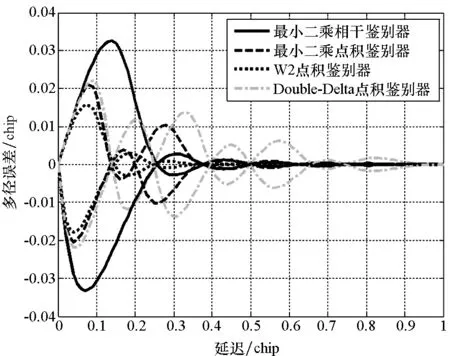
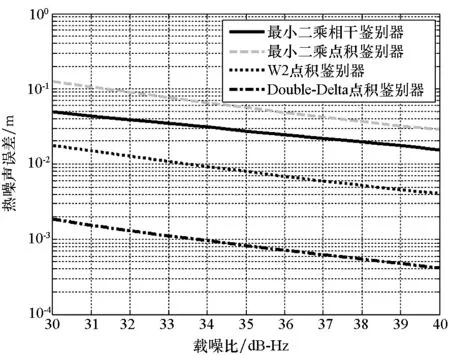
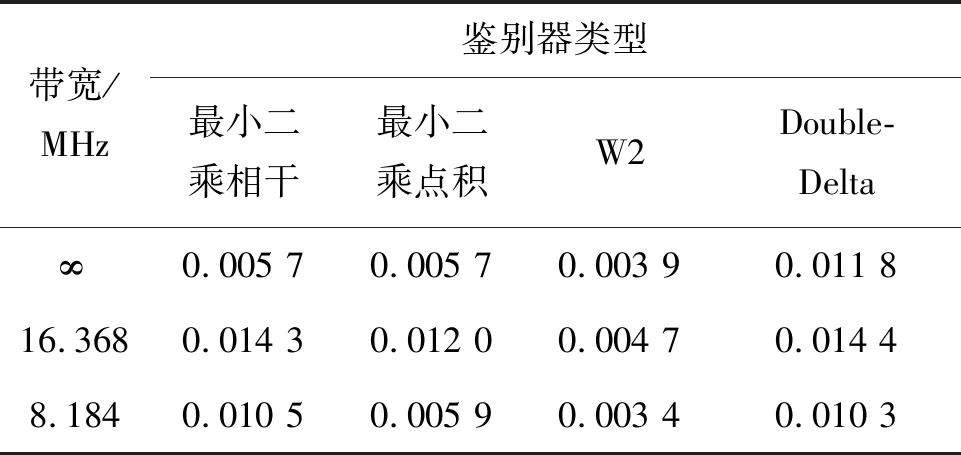
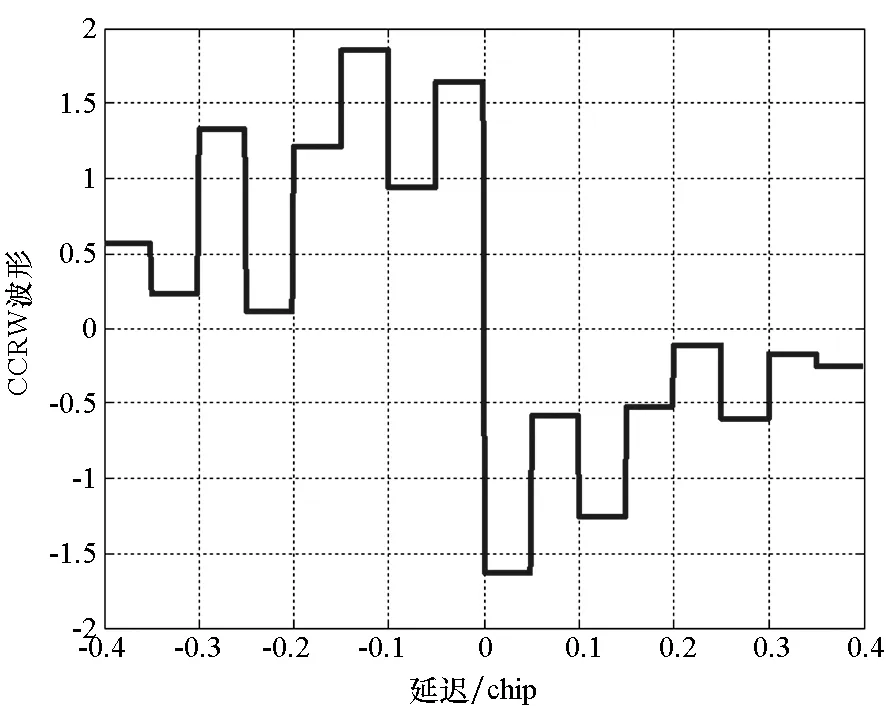
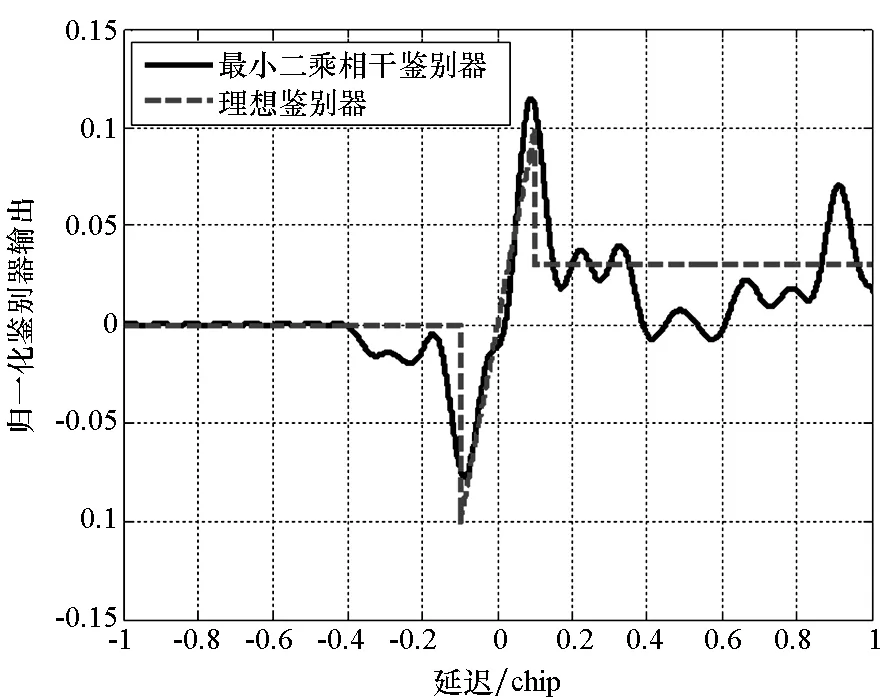
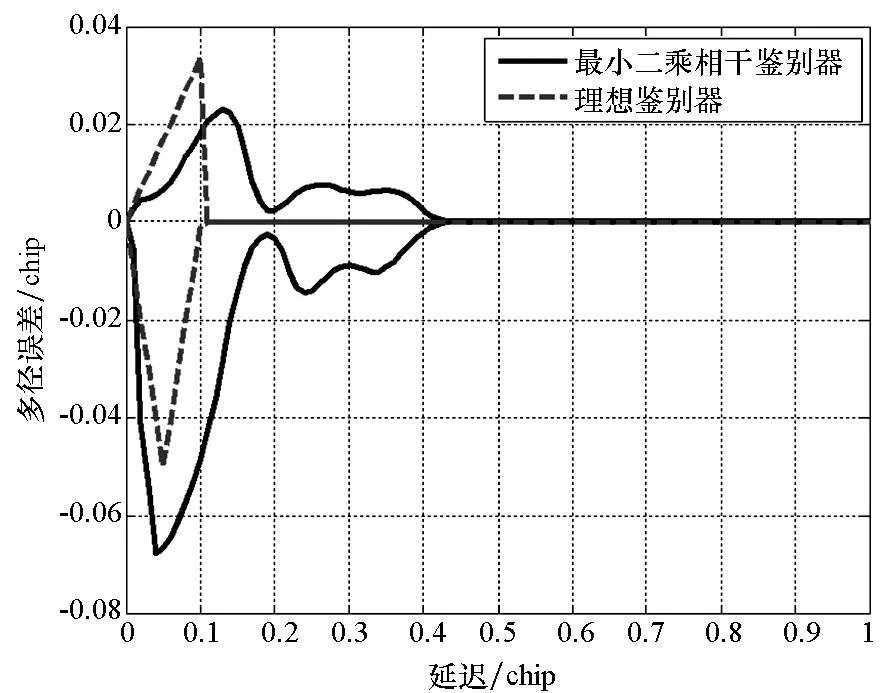
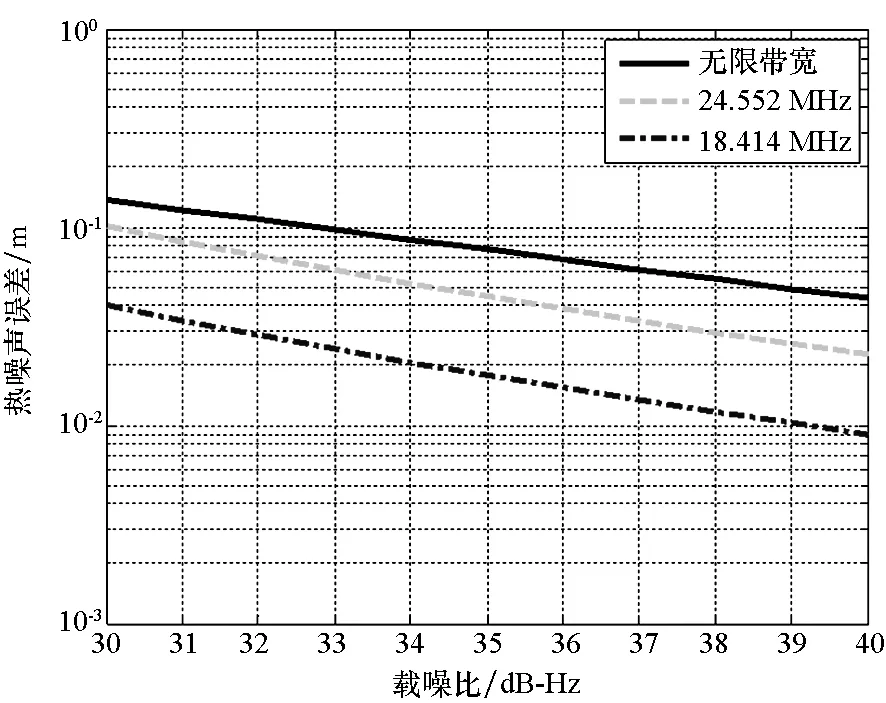
2)具有跟踪引导能力,在零点处具有一定的线性牵引范围,使信号可以收敛到零点,即ε∈[-pTc,pTc],0 3)具有一定多径抑制能力,即ε<-pTc时,D(ε)=0; 4)无其他稳定跟踪点,即ε>pTc时,D(ε)=b>0,b为常数。 根据上述准则设计的鉴别曲线如图3所示。将该形状的鉴别曲线作为BOC信号跟踪环路鉴别器的设计目标。 图3 设计目标鉴别曲线Fig.3 Target S-curve for design CCRW技术改变本地码波形为特殊的闸波信号,被称为参考波形。参考波形分为第一类和第二类参考波形。第一类参考波形可以表示为相关器的线性组合,等效于本地相关器设计;而第二类参考波形,则不能用相关器的线性组合表示。本文主要研究第二类参考波形的设计方法,其表达为: (2) 其中,g0(t)为基础方波,cj(t)指第j个扩频码片,Tc为码片宽度。 码相关参考波形设计如图4所示。码相关参考波形W(t)由N个经过di延时和γi加权的g0(t)组成,且出现在每个扩频码的翻转沿处。W(t)波形宽度不超过1个码片,μ为g0(t)的宽度。 图4 码相关参考波形设计Fig.4 Sample CCRW design CCRW技术通常在DLL中采用点积鉴别器,可表示为: (3) (4) 其中,T为相干积分时间。 =H(jω)X(jω)WΣ(jω) (5) (6) 其中, (7) 这时,CCRW的点积鉴别器可分别表示为: (8) 因此,CCRW鉴别器有两个主要设计参数:基本闸波偏移di和基本闸波幅度γi。通过固定并缩小偏移di间距,可将二维优化问题降为一维优化问题,即求解γ=[γ1,γ2,γ3,…,γN]T,且 (9) 其中,ε=[-STc, -STc+Δτ, -STc+2Δτ,…,STc]T。S为常数,M为ε的长度,Dideal(·)为目标鉴别曲线形状。 设di=-LTc+(i-1)μ,L≤1,Nμ≤Tc。则有: (10) 其中, (11) 式(10)的求解等价于线性方程组的求解。 PAx=b (12) 的极小范数最小二乘解为: (13) 式中:x为待优化的闸波幅度,根据最小二乘问题的研究,在最小范数意义下,x具有唯一解xLS=A†b;A†为A的广义逆。 求解最小二乘问题的经典方法为法方程法,即 A†=(AHA)-1AH (14) 通过求解AHA的逆矩阵即可得到最小二乘问题的解,AH为A的Hermite变换。矩阵A的条件数为: (15) 式中,σ1和σr为A的最大、最小奇异值,A的秩为r。法方程的条件数为κ(A)2,而系数矩阵A由于相关曲线的变化范围较小,往往是一个病态矩阵,使得系数矩阵或观测量出现微小变化δA和δb时,(A+δA)x=b+δb的解与Ax=b的解有明显的不同。 提出采用截断奇异值分解方法解决病态性问题,具体流程如下: 步骤1:对A进行奇异值分解,得到A=UΣVH,期中Σ=diag(σ1,…,σr,0,…,0),σ1≥…≥σr>0。 步骤2:设置不确定性度量阈值t。 步骤3:求解Ak=U1Σ1V1H,其中Σ1=diag(σ1,…,σk),U1、V1分别是U、V的前k列,使得σ1≥…≥σk>t>σk+1≥…≥σr。 预先设置的不确定性度量阈值t剔除了偏小的奇异值,抑制了病态矩阵的表达,使得该问题的求解具有较好的稳定性。 根据提出的最小二乘求解鉴别曲线算法,研究各阶BOC信号无模糊抗多径码相关参考波形,分析在不同带宽情况下的码相关参考波形性能,包括抗多径性能和热噪声性能。BOC(1,1)信号是BOC调制的代表信号;BOC(10,5)信号被用于现代化的GPS系统;MBOC(6,1,1/11)信号作为全球三大卫星导航系统的兼容互操作信号被广泛应用,而AltBOC(15,2.5)则用于Galileo系统的E5频段。因此,以BOC(1,1)、BOC(2,1)和BOC(6,1)信号为代表对本算法性能进行仿真。 图5显示了在无限带宽条件下的BOC(1,1)信号算法设计结果,目标鉴别曲线的牵引范围为±0.1 chip,在线性牵引范围之外,鉴别曲线在±1 chip内迅速下降至0。 如图5(a)所示,最小二乘相干鉴别器的波形设计结果与W2波形非常相似,在零点附近由相同的4个闸波组成,闸波面积和为0。闸波宽度分别为[0.01 chip,0.1 chip,0.1 chip,0.01 chip],闸波相对于本地码幅度归一化后,取值分别为[-10,1,1,-10]。在-0.5 chip附近有一个形状相同但幅值扩大1倍的闸波,闸波宽度分别为[0.01 chip,0.1 chip,0.1 chip,0.01 chip],闸波取值分别为[-20,2,2,-20]。这个新出现的波形,是为了抑制BOC(1,1)信号的自相关旁瓣而产生的。 最小二乘点积鉴别器的波形与相干鉴别器略有不同,闸波中间幅度不再固定,这是由信号的自相关函数导致的。 (a) CCRW波形(a) CCRW waveform (b) CCRW波形鉴别曲线(b) S-curve of CCRW图5 BOC(1,1)信号设计结果(非带限情况)Fig.5 Design results for BOC(1, 1) signal (band limited) 图5(b)为设计的鉴别器曲线,优化得到的最小二乘鉴别器曲线和W2鉴别器的线性区域区别较小,Double-Delta鉴别器具有2倍于其他鉴别器的过零点斜率,但是其在0.5 chip处有错锁点,W2鉴别器同样有一个错锁点。综合来看,优化得到最小二乘点积鉴别器曲线的线性区域较窄,且不具有错锁点。 BOC(1,1)信号的参考波形设计结果如图6(a)所示,在带宽6.138 MHz条件下最小二乘相干鉴别器和点积鉴别器的CCRW波形分布在-0.4~0.4 chip,两者波形形状与W2波形相近。该设计波形位置与BOC-Gated-PRN方式一致[12]。 BOC(1,1)信号的鉴别器曲线如图6(b)所示,各鉴别器的斜率大小相近。W2鉴别器由带限引起了鉴别器曲线的形变,降低了线性区域的范围。 (a) CCRW波形(a) CCRW waveform (b) CCRW波形鉴别曲线(b) S-curve of CCRW (c) 多径误差包络(c) Multipath error envelope (d) 跟踪精度(d) Tracking precision图6 BOC(1,1)信号CCRW波形(6.138 MHz)Fig.6 Design results for BOC (1, 1) signal (6.138 MHz) 多径误差包络曲线如图6(c)所示,此时最小二乘点积鉴别器的多径误差包络面积最大,而Double-Delta鉴别器多径误差包络面积最小。BOC(1,1)信号多径误差包络面积见表1,由表1可知,Double-Delta 鉴别器的多径误差包络面积是最小二乘相干鉴别器的17.0%,最小二乘点积鉴别器的46.8%,W2鉴别器的75.7%,BGP鉴别器的41.1%。 鉴别器的跟踪精度如图6(d)所示,最小二乘鉴别器的精度优于W2点积鉴别器,且最小二乘相干鉴别器与BGP鉴别器的差距小于0.01 m,说明窄带宽下,W2闸波的性能下降,而最小二乘方法可以取得更优的结果。 表1 BOC(1,1)信号多径误差包络面积 在8.184 MHz 带宽下,BOC(2,1)信号的设计波形如图7(a)所示,此时闸波的最小宽度为0.1 chip。最小二乘相干鉴别器和点积鉴别器的波形范围分别为[-0.8 chip,0.2 chip]和 [-0.4 chip,0.3 chip]。 如图7(b)所示,最小二乘鉴别器曲线除零点外无稳定跟踪点,但是线性区域左侧曲线面积大于W2闸波,因此多径误差包络面积更大。 由于带限效应,除W2鉴别器外,鉴别器的多径包络面积显著增大,如图7(c)所示,说明W2 (a) CCRW波形(a) CCRW waveform (b) CCRW波形鉴别曲线(b) S-curve of CCRW (c) 多径误差包络(c) Multipath error envelope (d) 跟踪精度(d) Tracking precision图7 BOC(2,1)信号设计结果(8.184 MHz)Fig.7 Design results for BOC(2, 1) signal(8.184 MHz) 鉴别器保持了较好的多径抑制性能。BOC(2,1)信号多径误差包络面积见表2,由表 2可知,W2鉴别器多径误差包络面积是最小二乘相干鉴别器包络面积的32.4%,最小二乘点积鉴别器包络面积的57.6%,Double-Delta鉴别器包络面积的34.6%。 W2点积鉴别器的跟踪精度明显优于最小二乘鉴别器,如图7(d)所示。 表2 BOC(2,1)信号多径误差包络面积 W2闸波和Double-Delta方法不再可用于高阶BOC信号。 在24.552 MHz带宽条件下,设计的码相关参考波形如图8(a)所示,闸波宽度为0.05 chip。 BOC(6,1)信号的鉴别器曲线如图8(b)所示,优化得到鉴别曲线存在一定的起伏,但是依然能够保证不存在错锁点。 在24.552 MHz带宽条件下,BOC(6,1)信号CCRW鉴别器的多径误差包络曲线如图8(c)所示,由于鉴别器精度和带宽限制,最小二乘鉴别器的误差包络比理想鉴别器更大。 图8(d)显示了鉴别器跟踪精度结果,带宽越窄,最小二乘相干鉴别器的跟踪精度越好,说明窄带宽下参考波形幅度较小,最小二乘方法在带宽受限条件下更加适用。 (a) CCRW波形(a) CCRW waveform (b) CCRW波形鉴别曲线(b) S-curve of CCRW (c) 多径误差包络(c) Multipath error envelope (d) 跟踪精度(d) Tracking precision图8 BOC(6,1)信号设计结果(24.552 MHz)Fig.8 Design results for BOC(6, 1) signal (24.552 MHz) 本文通过引入抗多径最优鉴别曲线的概念,建立满足多径抑制、去模糊、高精度和大动态范围的鉴别曲线设计规则,利用本地多相关器组合和参考波形,采用最小二乘逼近方法对鉴别曲线人为赋形,同时考虑通道的非理想特性对相关曲线形状的改变,从而实现了本算法在无模糊跟踪、跟踪精度和抗多径三项性能需求之间的平衡。 根据跟踪算法的两个重要评价准则,对本算法的性能进行了评估,一方面是考虑其多径抑制能力,另一方面则是考虑其热噪声性能。通过仿真分析可知,提出的最小二乘鉴别器性能与设计参数有关(如带宽、目标鉴别曲线等),为满足无模糊跟踪要求,可能导致降低抗多径性能和热噪声精度降低。以BOC(1,1)信号为例,6.138 MHz带宽下,设计的点积鉴别器包络面积相比W2鉴别器增加了61.8%,在不同载噪比下跟踪精度优于W2鉴别器4~5 dB。 该方法对于BOC信号的不同调制方式具有一定的通用性,可以作为卫星导航接收机DLL环路的BOC信号抗多径跟踪技术,并提供了BOC类信号满足去模糊、抗多径和高精度的接收机跟踪结构设计方法。
2 最小二乘模型
3 病态矩阵问题

4 设计结果与性能仿真
4.1 BOC(1,1)信号

4.2 BOC(2,1)信号

4.3 BOC(6,1)信号
5 结论
