一种用于雷达资源管理的目标雷达截面积预测算法

秦 童 戴奉周 刘宏伟



一种用于雷达资源管理的目标雷达截面积预测算法

秦 童 戴奉周*刘宏伟

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

在管理与优化雷达有限资源的应用中，目标的雷达截面积的起伏会对资源分配后的效果产生巨大的影响。针对该问题，该文提出一种对目标的雷达截面积进行预测的方法。该方法首先对回波进行处理以获取目标雷达截面积的测量值，进而通过概率密度转移的方法对目标在下一个时刻的雷达截面积进行预测。通过对来自3种飞机的雷达实测数据的计算，验证了该预测方法能够得到较为准确的预测值。最后，建立功率分配的优化方程，并通过仿真验证了对雷达截面积准确的预测能够提高功率分配后的测量精度。

雷达截面积预测；概率密度；资源管理

1 引言

近年来，相控阵雷达技术已经取得了快速的发展。这种类型的雷达可以灵活地改变发射波的照射方向，选择需要照射的目标，调整发射功率、驻留时间等参数。这些特性为我们提供了管理、优化雷达资源的可能性，进而可以对雷达资源进行合理的分配，从而达到节约雷达消耗功率，提高测量、跟踪精度，节约时间消耗等效果。

目前已有大量的关于雷达资源优化的研究工作，主要包括对雷达发射功率的优化与电磁波照射目标的驻留时间的优化。一般对于雷达资源进行优化的步骤是：(1)预测目标在下一个时刻的状态，包括目标的位置、雷达截面积(RCS)等。(2)根据预测的结果计算下一个时刻需要分配给各个目标的资源。(3)按照计算结果，调整雷达的发射参数，分配雷达资源。由此可见，对目标在下一个时刻状态进行预测的准确度，对于资源分配的效果具有至关重要的影响，但是对于目标RCS的预测，尚没有较为实用成熟的算法。

在目标飞行的过程中，雷达照射目标的视角是不断变化的。而对于形状较为复杂的目标，只要照射视角有变化，就会引起RCS较大的起伏[6]。在工程计算中常把目标的RCS视为一个定值，或者将RCS的起伏模型描述为统计模型，即施威林(Swerling)起伏模型。然而这些方法只能够提供RCS的取值范围或者某个固定的值，无法提供目标RCS在某个时刻的精确预测值。因此传统的估计RCS的方法无法完全满足资源管理方面实际应用的要求。

通过现有的对资源优化管理的研究[6]，可以看到，需要进行跟踪的目标中存在一定的距离雷达较远、回波信噪比较小的目标。进而在跟踪的过程中很难通过识别等方法获取目标的物理形态，同样难以通过文献[7~14]中的方法对RCS进行预测。以上文献中预测RCS的方法，都需要利用目标形状的先验信息，因此并不适合应用到资源管理的步骤中去。

综上，如何仅仅通过雷达的回波，获取、计算、预测目标的RCS仍是一个难题。针对在资源管理的过程当中，对目标信息了解有限的情况下，本文提出了一种预测目标RCS的方法。首先建立对目标的跟踪，通过回波获取目标当前时刻的RCS测量值，通过目标的航迹获取雷达照射目标的方向与目标飞行方向的夹角。接下来根据以上获取的历史信息，采用概率密度转移的方法，估计、预测目标在下一时刻的RCS。而后，为了验证预测RCS准确性对资源管理的影响，本文提出了对发射功率进行优化的方法。为了验证对RCS预测的准确性，本文采用来自3种飞机的雷达回波实测数据对目标的RCS进行预测。最后，采用仿真实验，验证了RCS预测方法的准确性以及优化发射功率对于提高测量误差的效果。

2 资源分配的分析

2.1 系统模型

2.2距离测量的克拉美罗下界(CRLB)

2.3 资源分配的影响因素

在跟踪的过程中，雷达对目标的测量误差需要保持在一个合适的水平。假设为期望的测量误差方差，则期望的对距离的测量误差方差

由式(7)可以看到，功率分配的有效性很大程度上依赖于预测的准确性。接下来，将对预测目标RCS的方法进行详细的描述。

3 RCS的预测

3.1 预测模型

目标RCS状态的先验概率表示为

3.2后验概率

则式(13)可以推导为

3.3状态转移概率

状态转移概率可以表示为

通过以上公式的推导，可以通过学习目标RCS的起伏趋势，利用概率转移的形式，对RCS进行预测。相比较传统的采用Swerling模型对目标的RCS进行估计的方法，本文采用的算法在获取目标信息有限的基础上，对RCS进行较为准确的预测。

4 功率分配

本算法针对的是多波束相控阵雷达，可以同时发射多个波束并跟踪多个目标，而雷达能够灵活地调整每个波束的指向与发射功率。接下来将对该类型雷达，设计照射目标的发射功率分配的方法。

考虑到需要在保证测量精度的前提下节约发射功率资源，以式(5)作为优化目标，即测量误差的方差接近一个固定的值。根据雷达的特性，同一时间内照射全部目标的发射功率之和有限，即，其中表示照射第个目标的发射功率，总计共有个目标。而表示雷达在同一时刻可以提供的总的发射功率。具体的优化方程可以描述为

将式(16)代入式(5)，得

5 实验结果及分析

本文将采用雷达实测数据对RCS的预测算法进行验证，并建立仿真，采用多种功率分配方法进行比较，以检验本文提出的功率分配结果的有效性。

5.1 RCS预测

本文采用雷达实测数据对RCS的预测算法进行验证，实测数据来自C波段雷达对3种不同的飞机进行照射产生的回波。3种飞机的具体参数如表1所示。

表1 3种飞机的参数

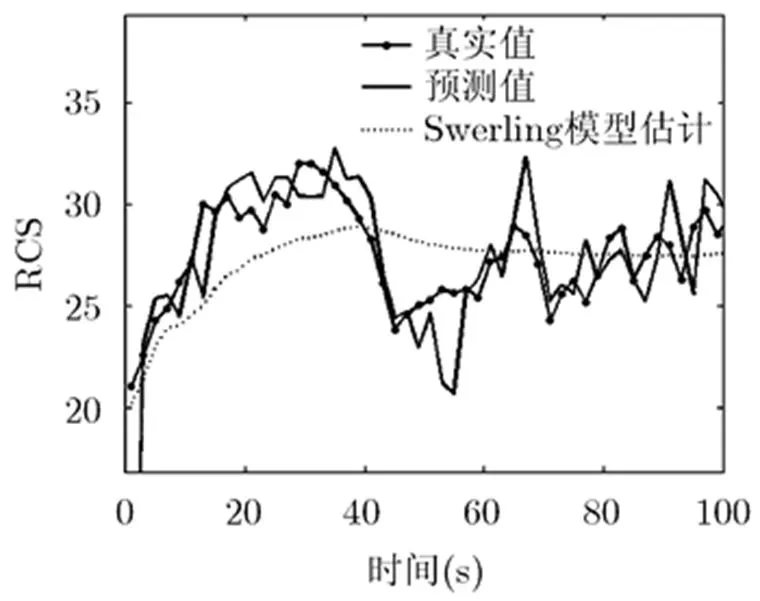
图1 安-26型号飞机RCS预测结果

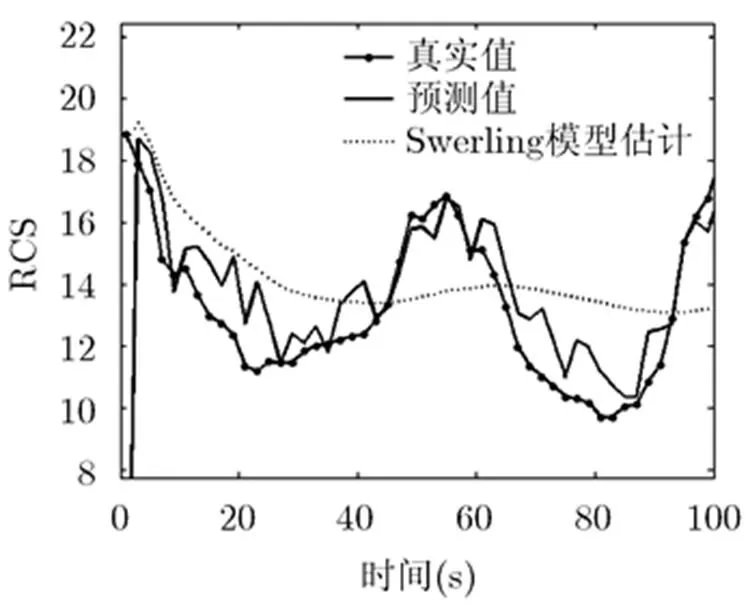
图2 雅克-42型号飞机RCS预测结果

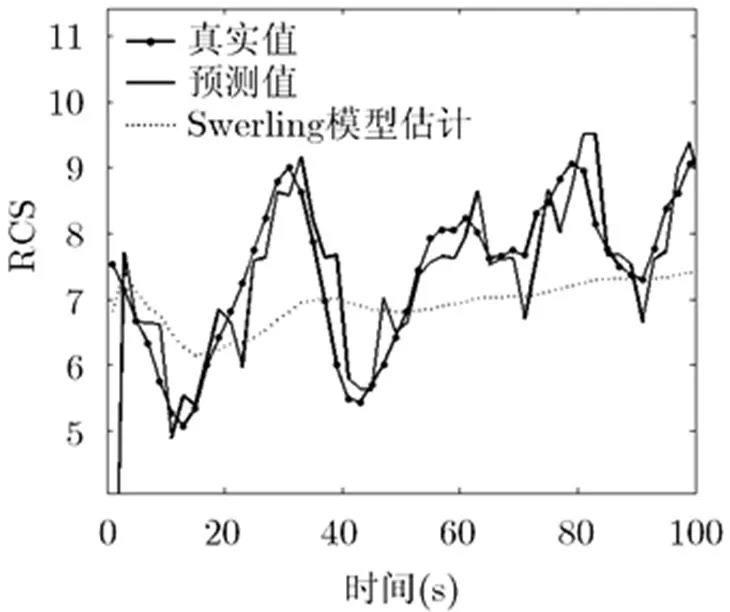
图3 奖状型号飞机RCS预测结果

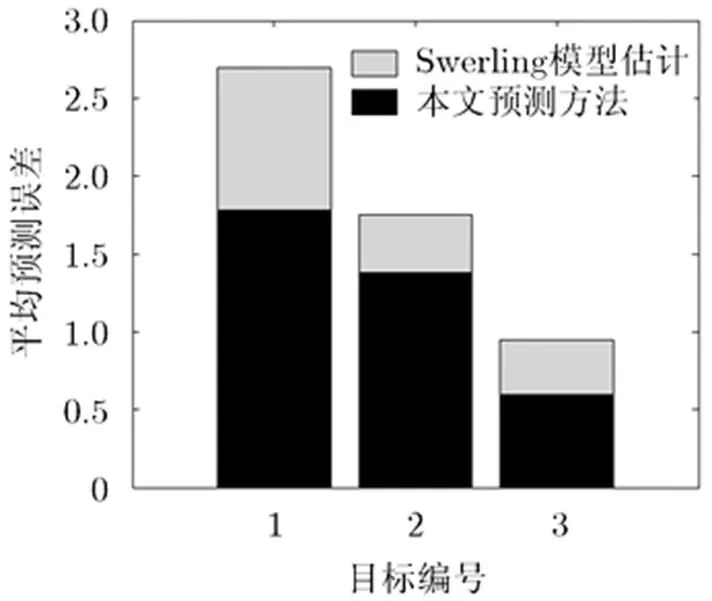
图4 3种飞机RCS平均预测误差

通过图1~图4中对3种飞机的仿真结果可以看出，采用本文的预测方法，可以较为准确地预测出目标RCS的起伏趋势，并进行较为准确地预测。相对于传统的采用Swerling模型对RCS进行估计的方法，本文的方法更加准确，进而保证了功率分配的准确性。

从图4可以看到，采用本文的方法对于不同的目标RCS进行预测，由于目标本身的原因，会对预测的效果产生巨大的影响。目标的形状越复杂，RCS的变化趋势越复杂，越难以预测，预测的误差越大。本次仿真所采用的3种飞机的回波数据中，安-26飞机是大型螺旋桨飞机，形状较为复杂，因此对RCS的预测误差较大。

接下来，本文将通过进一步的仿真，以验证说明影响本文算法预测RCS准确性的影响因素。本文将采用3组数据分别进行预测，3组数据情况为：

数据1：奖状飞机在300 s内的回波数据，重访时间间隔为1 s，回波信噪比为15 dB。

数据2：在数据1作为标准情况下，增加一定的噪声，使回波信噪比为11 dB，重访时间间隔为1 s。以此来模拟目标RCS起伏加剧对预测准确性的影响。

数据3：在数据1作为标准情况下，增大重访时间间隔为2 s。以此来模拟当目标运动产生的照射视角的变化率增大，对于预测结果准确性的影响。

则分别对3组数据进行预测，整个预测过程中，预测值与真实值的平均误差如图5所示。

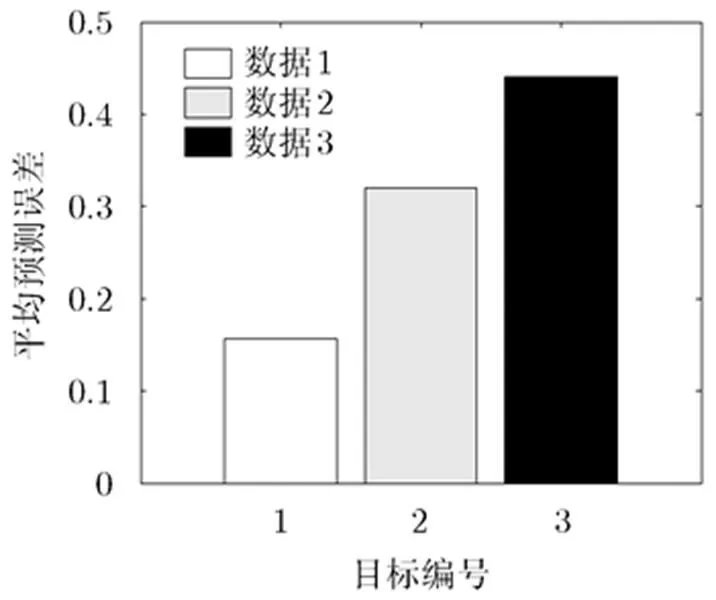
图5 3组数据预测结果的平均误差

通过仿真图可以看到，目标RCS起伏剧烈程度与雷达照射视角的变化率，均会直接影响本文预测算法的准确性。RCS起伏程度越剧烈、视角变化率越大，预测的误差越大。因此，本文算法适用于RCS起伏具有一定趋势，剧烈程度不大，飞行过程中视角变化率有限的目标。而在实际的使用过程中，可以将预测后的结果与实际量测进行比较，当预测误差超过门限，表明本文方法不适用当前目标。

5.2 功率分配

在仿真场景中，共有3个目标在雷达视线范围内飞行。本文采用3种发射功率分配的方法，来进行仿真与比较。首先采用第3节的预测目标RCS的方法与第4节中功率分配的方法，对雷达照射目标的电磁波发射功率进行分配，经过功率分配后，雷达对3个目标实际的测量误差如图6所示。接下来采用传统的Swerling模型方法对目标RCS进行估计，并采用式(17)对功率进行分配，分配后3个目标的跟踪误差如图7所示。最后采用平均分配功率的方法，即照射3个目标的发射功率相同，则对3个目标实际跟踪误差如图8所示。仿真中设置的期望的对目标测量的误差为200 m，即式(5)中。

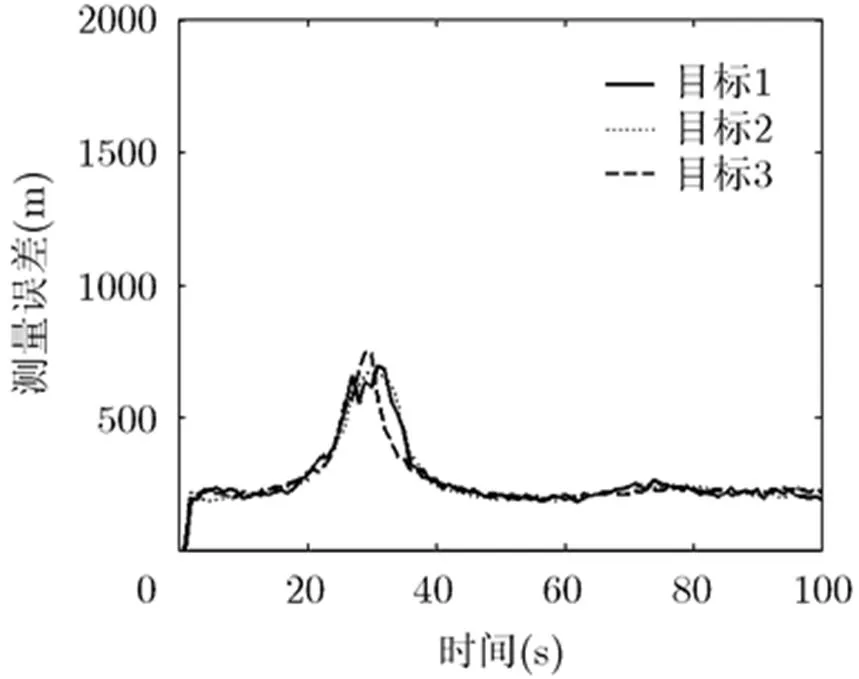
图6 预测RCS并进行功率优化后的测量误差

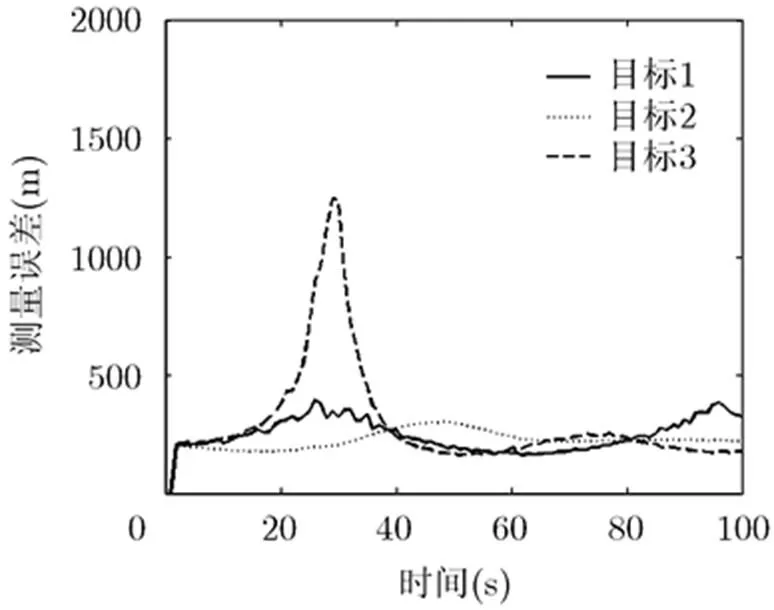
图7 Swerling估计RCS并进行功率优化后的测量误差

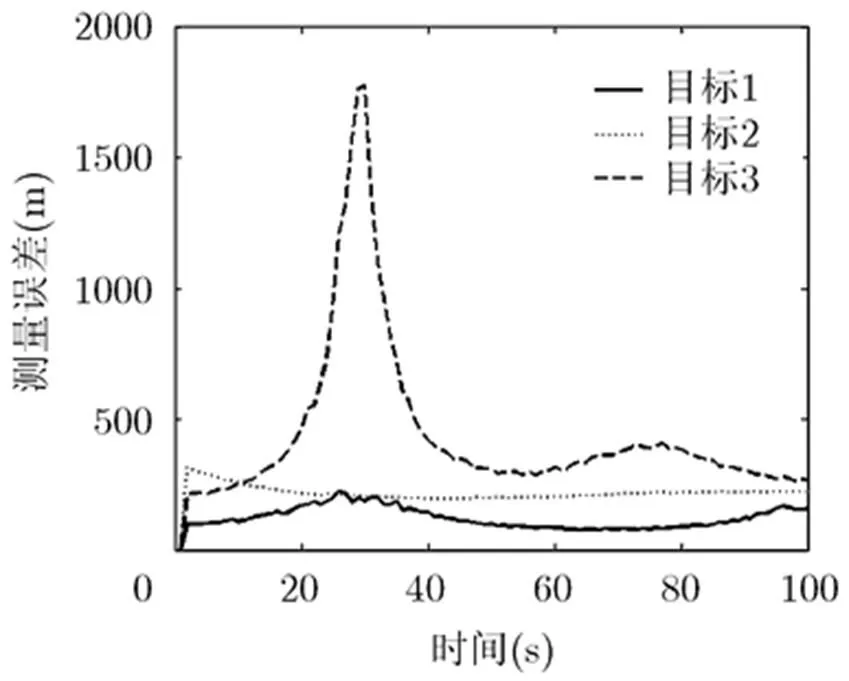
图8 平均分配功率后的测量误差

通过图6可以看到，采用本文提供的方法对RCS进行预测，由于有较为准确的RCS的预测值，故而经过功率分配后，得到的测量误差基本处于期望的误差取值附近。而通过图7可以看出，虽然采用相同的功率分配准则，但是由于采用了传统的Swerling模型对RCS进行估计，RCS的预测不准确，导致功率分配的不准确，进而导致了目标3的测量误差较大，超出了期望的范围。通过图8可以看出，采用平均分配功率的方法，目标3的测量误差过大，存在丢失目标航迹的可能。

通过以上对比仿真可以看出，通过本文的方法对目标在下一时刻的RCS进行预测，可以得到较为准确的预测值，进而能够进行较为准确的功率分配，保证对目标的测量误差处于合理的范围内。若采用传统的Swerling模型的方法对RCS进行估计，由于估计值的不准确，导致经过功率分配后得到的测量误差的结果并不理想。

6 结束语

本文研究了雷达在对目标的跟踪过程中，对目标的RCS进行预测，并将预测结果应用到功率分配的问题。首先，本文采用概率密度转移与变化趋势学习的方法，推导了对目标RCS的预测方法。而后，本文提出了一种雷达电磁波照射目标的功率分配方法，并推导出目标RCS预测的准确性对于功率分配结果的影响。进而，通过3种飞机的实测数据，验证了本文方法能够对RCS进行较为准确的预测。最后，通过仿真对3种分配方法的比较，验证了本文的分配方法对于控制跟踪误差，节约资源的有效性。

参考文献

[1] 严俊坤, 纠博, 刘宏伟, 等. 一种针对多目标跟踪的多基雷达系统聚类与功率联合分配算法[J]. 电子信息学报,2013, 35(8): 1875-1881.

Yan Jun-kun, Jiu Bo, Liu Hong-wei,.. Joint cluster and power allocation algorithm for multiple targets tracking in multistatic radar systems[J].&, 2013, 35(8): 1875-1881.

[2] Godrich H, Petropulu A P, Vincent H,.. Power allocation strategies for target localization in distributed multiple-radar architectures[J].,2011, 59(7): 3226-3240.

[3] Elshafei M and Hanif D. Radar pluse interleaving for multi-target[J].,2003, 6(10): 101-103.

[4] Ghosh S, Hansen J, Rajkumar R,.. Integrated resource management and scheduling with multi-resource constraints [C]. Real-Time Systems Symposium, Lisbon, 2004: 25-37.

[5] Li W L and Yuan S. Efficient anchor power allocation for location-aware networks[C]. IEEE International Conference (ICC), Kyoto, 2011: 1-6.

[6] Inasawa Y, Saito M, Naito I,. Numerical calculation and experimental validation of RCS analysis for radome-enclosed scatterer by using PMCHWT- formulation[C]. 2011 General Assembly and Scientific Symposium, Istanbul, 2011: 1-4.

[7] Altm N and Yazgan E. RCS prediction using fast ray tracing in plucker coordinates[C]. 2013 7th European Conference on Antennas and Propagation, Sweden, 2013: 284-288.

[8] Chan K K, Wong S, Riseborough E,RCS predictions and measurements of a full size jet engine model[C].Antennas and Propagation Society International Symposium,Memphis, 2005: 97-100.

[9] El-Kamchouchy H, Saada K S, Hafez A E S,An accurate multistatic radar RCS for airhawk F117 stealthy target[C]. 15th International Conference on Computer Modelling and Simulation, Cambridge, 2013: 734-738.

[10] Sun Bin, Wang Xue-zhi, Moran B,.. Target tracking using range and RCS measurements in a MIMO radar network[C]. Radar Conference 2013, Beijing, 2013: 1-6.

[11] Jeong Ho-ryung, Lee Dong-han, Oh Tae-bong,. RCS measurement and analysis of corner reflector and its background for KOMPSAT-5 calibration and validation[C]. 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar(APSAR), Seoul, 2011: 1-4.

[12] Mertens M and Ulmke M. Ground target tracking with RCS estimation utilizing probability hypothesis density filters[C]. 16th International Conference on Information Fusion, Istanbul, 2013: 2145-2152.

[13] Tong Jun, Shan Gan-lin,. Decomposition of maneuvering target RCS based on wavelet analysis[C]. 2010 First International Conference on Pervasive Computing, Signal Processing and Applications. Hangzhou, 2010: 972-976.

[14] Li Yong, Li Wen-zhu, Yuan Li,. Research on RCS characteristic of three kinds of metal plat[C]. 2012 IEEE 2nd International Conference on Cloud Computing and Intelligent Systems (CCIS), Hangzhou, 2012: 875-878.

[15] Kay S M著. 罗鹏飞, 张文明, 刘忠, 等译. 统计信号处理基础估计与检测理论[M]. 第1版, 北京: 电子工业出版社, 2011: 44-47.

Radar Cross Section Prediction Method for Radar Resource Management

Qin Tong Dai Feng-zhou Liu Hong-wei

(,,’710071,)

In the application of planning and management of the limited resources of radar, the fluctuation of the target’s Radar Cross Section (RCS) area will have a significant impact on the effects of allocation of resources. For this problem, this paper puts forward a prediction of target radar cross section method. This method firstly gets the measurement of the target’s radar cross section, and predicts the value by using the method of probability density transfer. Based on the calculation of radar measured data from three types of aircraft, the method can get more accurate prediction. Finally, the optimization of power distribution equation is built and simulation results demonstrate that the accurate prediction of the RCS will improve the measurement accuracy after the power allocation.

Radar Cross Section (RCS) prediction; Probability density; Resource management

TN953

A

1009-5896(2015)08-1849-06

10.11999/JEIT141466

戴奉周 fzdai@xidian.edu.cn

2014-11-24收到，2015-05-07改回，2015-06-08网络优先出版

国家自然科学基金(61271291, 61201285)，新世纪优秀人才支持计划(NCET-09-0630)，全国优秀博士学位论文作者专项资金(FANEDD- 201156)和中央高校基础本科研业务费专项基金资助课题

秦 童： 男，1988年生，博士生，研究方向为目标跟踪、认知雷达资源管理等.

戴奉周： 男，1978年生，副教授，研究方向为统计与自适应信号处理、目标检测等.

刘宏伟： 男，1971年生，教授，研究方向为雷达信号处理、雷达自动目标识别、认知雷达、协同探测等.