多普勒频移修正下的快速伪码捕获技术的实现

王守亚，吴 琰

(淮南师范学院电子工程学院，安徽 淮南 232038)

0 引言

扩频通信是当今三大高技术通信方式之一，主要是为了提高信息传输的可靠性而提出的一种不同于常规通信系统的新理论和技术[1]。开始主要在抗干扰通信和保密通信中有广泛应用。其中，直接序列扩频是扩频通信中最常见的通信方式，具有抗干扰能力强、保密性强、抗衰落性能好和具有码分多址能力等。伪码捕获技术是扩频通信研究的重点和热点。伪码捕获是伪码同步的粗同步，捕获成功后，进行伪码跟踪，精准同步。最初，具有代表性的伪码捕获法有滑动相关捕获法[2]和并行捕获法[3]，滑动相关捕获法是一种比较经典的算法，它的优点是算法实现简单、对硬件资源的要求较少，但是存在捕获时间长的缺点，适合短码、低动态的情况，而并行捕获法虽可以缩短捕获时间，但是硬件资源需求过多，特别是在伪码周期较长的情况下，缺点更为突出。后期，又出现了匹配滤波器捕获法[4]和频域变换捕获法[5]等，但是都存在捕获时间长、硬件资源浪费、低信噪比环境下难以实现伪码捕获或受多普勒效应影响较大等问题，尤其当伪码的周期较长和捕获环境较差时，传统伪码捕获法的应用受到了很大的限制。如何克服这些困难，成为了伪码捕获技术研究的热点。传统的伪码捕获，都是基于时域的思想实现的，而基于FFT的伪码捕获[6-8]是在频域中完成伪码捕获的，借助于FFT的快速运算，可以在很大程度上缩短运算时间，相当于降低了捕获时间，如果在利用FFT进行伪码快速捕获时，能够较好地克服多普勒频移带来的影响，将是伪码捕获技术的大进步。

1 多普勒频移对伪码捕获的影响

伪码具有良好的自相关特性，当伪码同步时，进行相关运算后，会输出尖锐的峰值，不同步时，输出结果会很小，伪码的这一特性，是扩频信号捕获的依据。当本地伪码与接收信号的伪码相位相差在一个很小的范围内时，通常取相差不超过一个码片，经相关运算后，会得到一个最大的相关输出，当这个输出结果大于设定的门限值时，可以判定伪码初步同步，即捕获成功。但是，如果本地载波和接收载波的频差较大，就算伪码同步，也很难得到超过门限值的相关输出，会严重影响本地伪码与接收伪码相关运算的结果，导致难以捕获成功，所以，需要调整本地载波，减小与接收载波之间的频差，这是实现伪码捕获的前提条件[9]。

由于扩频通信中应用的技术和别的通信技术有着较大的区别，具有其他通信系统无法达到的优良性能，最初应用在军事通信中，所以在实际应用中，大多都处于高动态的环境下，工作的环境比较复杂多变，接收机和发射机不可能在一个固定的位置，它们之间的距离往往是不断变化的，存在着相对移动，会造成发信机和收信机载波频率的变化。这种情况下，在伪码捕获过程中，只是单纯的保证伪码同步，还无法得到输出的相关峰值，这主要是受到多普勒效应的影响，使得接收信号经混频滤波后仍残留频差。

为了解决多普勒频移对伪码捕获的影响，在伪码同步时，能够得到相关峰值，在接收端以步进量Δf来改变本地载波，步进量的值可正可负，一般在一个对称的范围内进行变化，通过步进量逐步改变本地载波，一直到本地载波和输入信号载波的相位差值小到一定的程度，相关器将会出现相关峰值。本地载波和伪码在若干次的不断调整后，会和输入的扩频信号相位一致，相关器输出峰值，将相关峰值与设定的门限值相比较，若相关的峰值超过门限值，则认为捕获成功。否则，重复上述过程，直到捕获成功。

考虑一个数据调制一个伪码周期的情况，对接收信号以码片速率进行采样，为了方便研究多普勒频移对伪码捕获的影响，此处不考虑噪声的影响。则经过数字混频滤波后的接收信号可以表示为：

r(nTc)=Ad(nTc)c(nTc)ej(2πfdnTc+θ)，

(1)

式中：n为正整数；A为信号的幅值；d(nTc)为取值±1的数据码元信号；c(nTc)为取值为±1的伪码信号；Tc为码片的周期；fd为多普勒频移量；θ为随机相位。

通常情况下，本地产生的伪码序列和接收信号的伪码序列不同步，存在相位差，为了更清晰地体现出多普勒频移对伪码捕获的影响，假设本地伪码和接收码已经完全同步。可以得到一个伪码周期内的相关输出的值为：

(2)

令信号的幅值A=1，并不影响研究结果。对公式(1)进行计算化简，最后得到相关器输出的归一化幅频响应为：

(3)

R(fd)表示多普勒频移对相关峰值的影响，这里取如下参数进行仿真，伪码长度M=1 023，伪码速率Rc=1.023×107Hz，Tc=1/Rc，0≤fd≤4×104Hz，得到相关器输出的归一化幅频响应如图1所示。

从图1可以看出，只有在没有频偏，即多普勒频移值为0的情况下，相关峰值才为1，此时，本地产生的伪码和接收的伪码处于完全同步的状态，相关输出峰值最大。整体上看，随着频偏的增加，相关峰值逐渐减小，在很大程度上影响了伪码捕获的结果。相关器的幅频响应决定了允许残留的载波频率的最大值，同时也决定了载波多普勒频移的步进量，只有以合适的步进量对多普勒频移进行有效的补偿，才能够快速准确地实现伪码捕获。

2 多普勒频移对FFT伪码捕获的影响

基于FFT的伪码捕获法主要利用FFT运算进行相关，把本地伪码与接收伪码进行相关运算的结果作为输出，由伪码的自相关特性可知，相关运算会有一个峰值，此时，对应本地伪码与接收伪码同步。对于实现较长周期的伪码捕获，在时域中进行相关运算需要的运算量非常大，可以把时域的运算转化到频域，利用FFT进行快速运算。一次时域的相关运算可以转换成两次的FFT和一次的IFFT运算，有效降低运算的复杂度，这样可以节约大量的运算时间，快速地获得相关运算的结果[10]。设两个输入的序列分别为x(n)和h(n+τ)，长度都是N，时域循环相关运算的结果为y(τ)，如图2频域相关原理图，得：

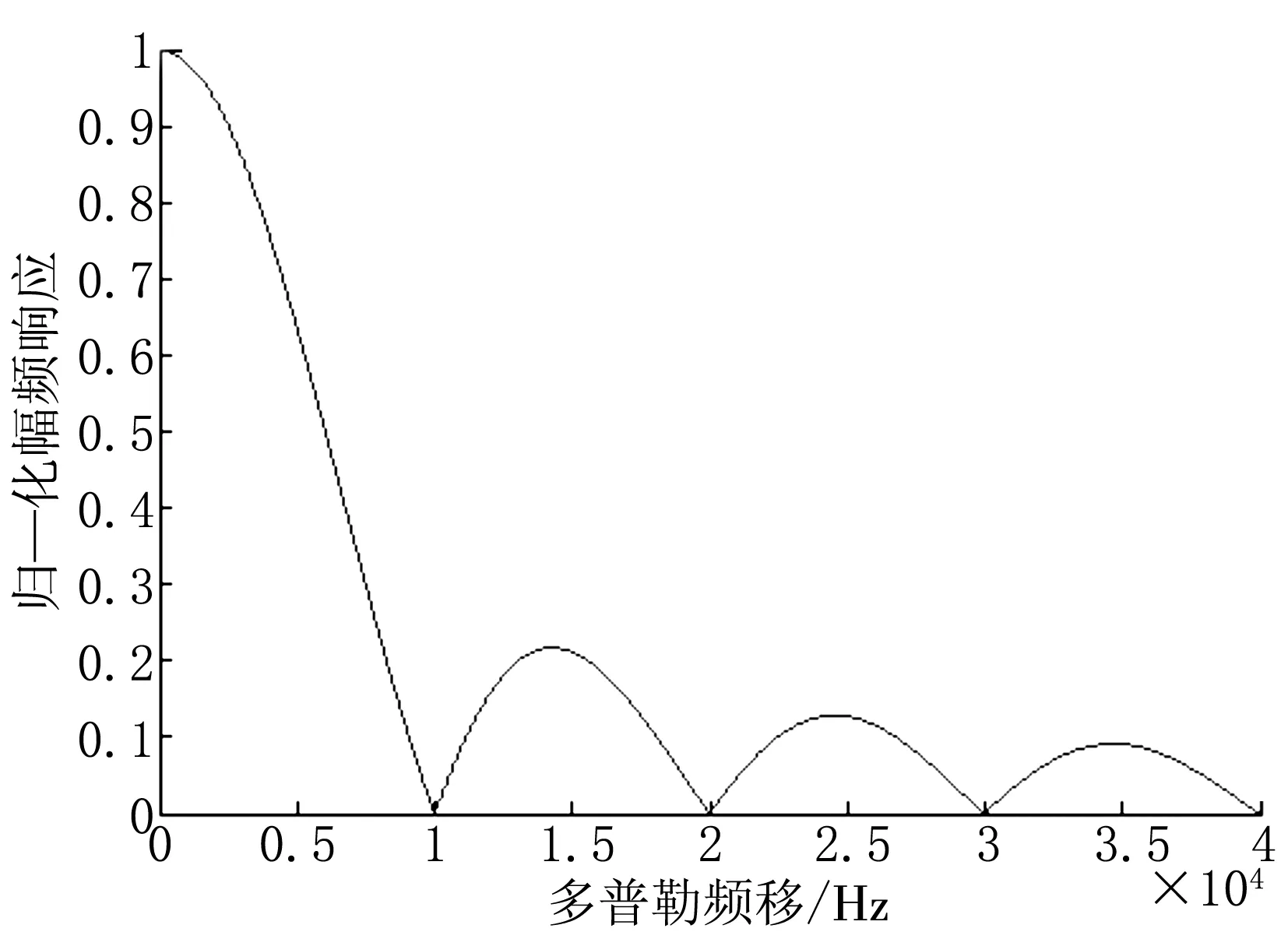
图1 多普勒频移对相关峰值的影响

图2 频域相关原理图

y(τ)=∑x(n)h(n+τ)=x(n)⊕h(-τ)=F-1(F[x(n)](F[h(n)])*)。

(4)

如果x(n)是接收的PN码序列，h(n+τ)是本地产生的PN码序列，根据PN码的自相关特性，当接收码与本地码同步时，y(τ)的值最大，表示接收码与本地码同步。

当时域的相关运算转换成频域的FFT运算时，一次FFT运算需要N/2*log2N次乘法运算，从图1可以看出，一次完整的FFT循环相关，需要3次FFT和1次复数相乘，需要的运算量为3N/2*log2N+N，而在时域计算的话，需要的运算量为N2。当N较大时，这种运算方法可以节约大量的时间，FFT循环相关的优化效果也就越明显。所以可以把FFT运算引入到伪码捕获中，实现快速的伪码捕获。

利用FFT运算实现快速伪码捕获，多普勒频移会对这种捕获方法造成一定的影响。具体分析如下：

把接收到的信号与本地产生的伪码信号分段做并行相关运算，设码长为M，每一个子段长为L，总共分成P=M/L段，对每个子段做N点的FFT运算，将N个输出分别和设定的门限值做比较，如果有任何一个输出值超过了设定的门限值，就认为本地伪码和接收伪码同步，实际上，这种情况下，二者之间的相位还存在一定的差距，可以借助超过门限设定值的点的位置对多普勒频移的值做出初步估计，对本地的载波进行一定程度的修正，在满足相关结果超过门限值且频差足够小时就认为捕获成功；如果输出值都比设定的门限值小，就需要滑动本地的伪码序列，继续下一次的相关运算，直到捕获成功。为了方便研究多普勒频移对FFT捕获结果的影响，假设码相位已经同步。结合式(1)，此时θ=0，设A=1，d(nTc)=1，可得：

r(nTc)=c(nTc)ej(2πfdnTc)，

(5)

设本地的伪码序列为c′(nTc)，在码相位同步的条件下，得：

r(nTc)*c′(nTc)=c(nTc)ej(2πfdnTc)*c′(nTc)=ej(2πfdnTc)，

(6)

第i个分段的相关输出值为：

(7)

对式(7)做FFT运算，结果取绝对值，并归一化得：

(8)

P(k)的值表示多普勒频移对FFT第i点输出峰值产生的影响，如果第k个FFT输出值超过设定的门限，就表明伪码已经实现初步同步，通过k值的大小，计算出多普勒的频移量为：

(9)

这里取如下参数进行仿真，伪码长度M=1 023，子段长度L=256，N=8，伪码速率Rc=1.023×107Hz，Tc=1/Rc，得到多普勒频移与FFT相关输出的关系如图3所示。

从图3可以看出，随着多普勒频移的增大，FFT的相关峰值也会逐渐下降，会在很大程度上影响伪码捕获的结果。如果接收信号的多普勒频移为一个固定值，只要有一个相关峰值超过设定的门限值，就可以利用式(9)估算出接收信号载波与本地载波的频率差值，然后通过合适的步进量对本地载波进行不断的修正，直到差值足够小。

3 多普勒频移补偿下的FFT捕获的实现

在实际的伪码捕获中，接收机大多都是在动态的环境下工作的，多普勒频移的产生是不可避免的。通过前面的仿真，可以看出多普勒频移对相关峰值输出的影响，要想完成捕获工作，就需要对本地载波进行适当的修正，这样可以减小或消除多普勒频移对捕获的影响。具体实现框图如图4所示。

图3 多普勒频移与FFT相关输出的关系

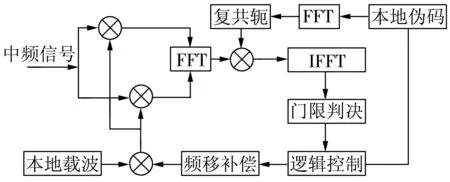
图4 加频移补偿的FFT伪码捕获法框图

算法的实现步骤如下：

1)对本地信号和接收信号分别进行采样后做FFT运算，运算结果分别为C(k)和R(k)，接着求C(k)的复共轭C*(k)，把R(k)与C*(k)相乘的结果再做IFFT运算；

2)把1)中IFFT运算的结果送入门限判决器，和预先设置的门限值做比较，进行判决，根据判决结果控制逻辑控制电路；

3)如果IFFT运算的结果大于门限值，认为捕获成功，接收信号与本地信号同步，此时通过逻辑控制电路来控制频移补偿电路，则不需要对本地载波进行频移补偿；如果IFFT运算的结果小于门限值，认为捕获失败，此时通过逻辑控制电路来控制频移补偿电路，对本地载波进行修正，一直到捕获成功为止，进行修正时，要以一个合理的步进值进行修正，如果步进值选择较大，可能会出现相关值都不大于门限值的情况，无法实现伪码捕获，如果步进值选择较小，会造成捕获时间长的问题，降低了捕获效率。

以伪码长度M=1023，信息码源速率Ra=10 kHz，伪码速率Rc=10.23 MHz，多普勒频移fd=10 kHz为例，这里综合考虑补偿效果和捕获时间，多普勒频移的修正值定为fx=1 kHz，分别在信噪比SNR=0和SNR=-25 dB的环境下进行快速伪码捕获，捕获效果如图5～6所示。

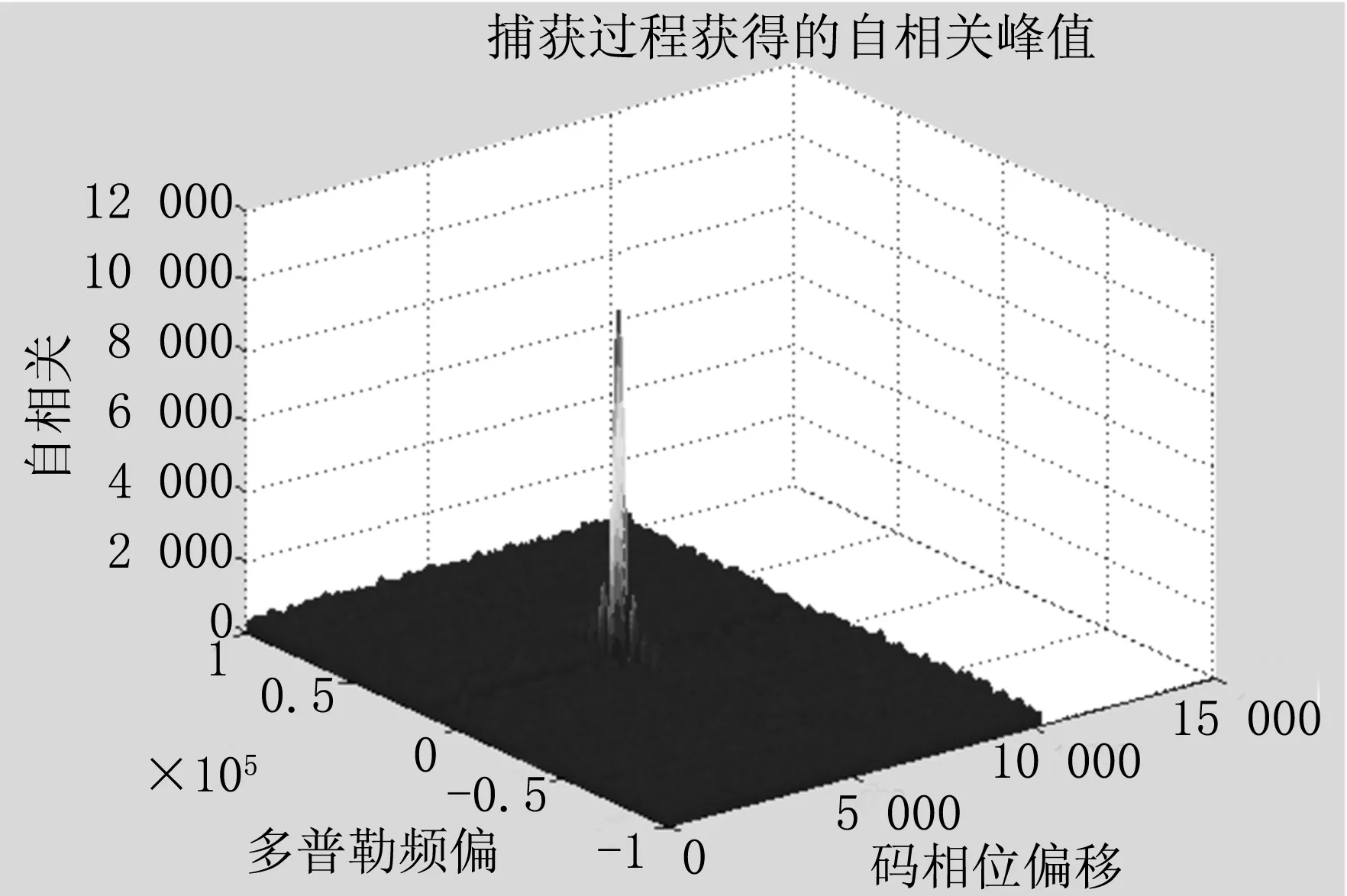
图5 SNR=0时的伪码捕获结果

图6 SNR=-25 dB时的伪码捕获结果

从仿真结果可以看出，在合理选择修正值的基础上，对FFT的快速伪码捕获法进行多普勒频偏的补偿，可以很好地实现伪码捕获，并且在低信噪比环境下也有较好的捕获效果。

4 结语

由于多普勒频移对伪码捕获的结果影响较大，而且是不可避免的，减小或消除多普勒频移造成的影响是非常必要的。本文详细分析了多普勒频移对伪码捕获技术的影响，并给出了解决办法，选择合适的步进值，对本地载波进行频移补偿，在不断的修正后，最终实现伪码的快速捕获。通过仿真显示，频移补偿后，此方法在较大多普勒频移和较低信噪比环境下实现伪码捕获有良好的表现，达到了预期的效果。