基于多鉴别器生成对抗网络的时间序列生成模型

陆彦辉，柳寒，李航，朱光旭

（1.郑州大学电气与信息工程学院，河南 郑州 450001；2.深圳市大数据研究院，广东 深圳 518115）

0 引言

近年来，随着计算能力的提升和5G 网络的普及，数据生成规模逐步扩大，在生产生活中的作用也日益显著。越来越多的商业公司和组织机构依赖于大数据分析得到有效的决策[1]。大数据分析中一个重要类别是分析与时间相关的数据，涉及金融、气象、石油和医学等多个领域。例如，通过分析金融时间序列来预测股票价格[2]；通过分析气候时间序列来分析植被的变化[3]；通过分析石油产量时间序列来预测石油的产量[4]；通过分析COVID-19 随时间变化的确诊人数来预测未来的确诊人数[5]。

时间序列是按照一定的时间间隔持续记录一段时间的数据，它们通常包含着丰富且复杂的信息，具备较强的研究和商业价值。然而，这些数据在收集过程中存在着各种各样的问题，例如，数据往往包含隐私信息，无法进行公开传播与实验[6]；传感器数据在收集过程中存在数据缺失[7]；数据收集困难导致可用数据集过小，难以满足模型训练需求[8]。一种可行的解决方案是通过机器学习方法生成大量与真实数据相似度较高的数据，从而满足模型训练、验证等应用。

现有基于机器学习的生成模型主要包括变分自动编码器（VAE,variational auto-encoder）[9]和生成对抗网络（GAN,generative adversarial network）[10]。其中，GAN 的研究得到了广泛的关注，已有工作提出了多种GAN 模型，可用于生成逼真的图像和视频。鉴于GAN 在图像生成方面的优异性能，开发高质量、多样化和特殊性的时间序列数据的工作得以进一步展开。

本文采取多鉴别器对时间序列的多种特征进行鉴别，提出了多鉴别器生成对抗网络（MDGAN,multi-discriminator generative adversarial network）模型。本文主要研究工作如下。

1) 本文提出了一种新型的MDGAN 模型，包含时域鉴别器、频域鉴别器、时频域鉴别器和自相关鉴别器，能够对生成数据进行多角度评估，进而提高生成器的合成数据质量，使合成数据更加符合真实时间序列的分布和特征。

2) 在对所提模型进行训练时，本文引入了二分类交叉熵模型，优化了原始的GAN 损失函数，使其适配多鉴别器网络，从而提升了模型训练效果。

3) 本文采用了不同类型的数据集对模型进行横向和纵向的对照实验，验证了本文所提模型能够有效提升合成时间序列的质量。

1 相关工作

生成对抗网络最早由Goodfellow 提出，其核心主要体现了零和博弈思想。在生成对抗网络中，同时训练生成器网络和鉴别器网络这2 个网络。整个网络的损失函数定义为

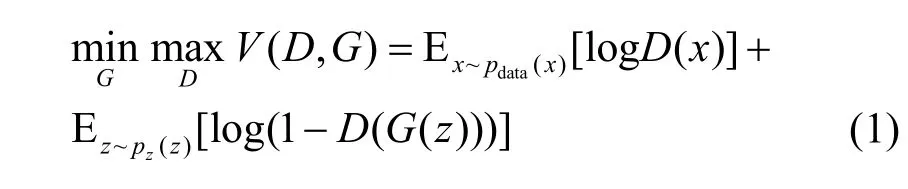
其中，pdata表示真实数据x的分布，符合随机分布pz的噪声z表示生成器的输入，G(z)表示生成器生成的合成数据，D(·) 表示鉴别器对数据的评价结果，E 表示数学期望。生成器致力于学习真实数据的特征，以此生成符合真实数据分布的合成数据；鉴别器致力于分辨输入是来源于真实数据还是合成数据。在训练鉴别器的过程中，希望真实数据x通过鉴别器的结果D(x)更接近真实的评价，合成数据G(z)通过鉴别器的结果D(G(z))更接近虚假的评价。而在训练生成器的过程中，希望合成数据G(z)通过鉴别器的结果D(G(z))更接近真实的评价。当训练达到纳什平衡时，认为生成器的合成数据的主要特征已经符合真实数据的主要特征。

现有工作以GAN 为基础进行了不同方面的改进。Radford 等[11]提出的深度卷积生成对抗网络（DCGAN,deep convolutional generative adversarial network）将卷积神经网络应用到GAN 中，在网络架构上改进了原始GAN。Arjovsky 等[12]提出的WGAN（Wasserstein generative adversarial network）采用Wasserstein 距离指导整个模型的训练，在鉴别器中使用权重剪枝技术。Isola 等[13]提出的基于GAN 的Pix2Pix 算法用于图像像素间的转换，利用条件生成对抗网络（CGAN,conditional generative adversarial network）生成图像。Zhu 等[14]提出了循环一致性生成对抗网络（CycleAN,cycle-consistent adversarial network），以Pix2Pix 为基础，主要应用于非配对的图片生成和转换，可以实现图片的风格转换。Karras 等[15]提出了可以控制样式的StyleGAN（style-based generator architecture for generative adversarial network），通过修改样式的特定尺度来控制图像的生成。现有工作已经将GAN 成功应用于图像、视频以及自然语言等方向。

循环神经网络（RNN,recurrent neural network）具有独特的环状结构，很适用于处理连续时间序列[16]。然而它缺乏学习长期依赖关系的能力，而这种关系对于根据过去预测未来是至关重要的。RNN 的变体长短期记忆（LSTM,long short term memory）网络具有长时间记忆信息的能力，进而可以学习序列信息的长期依赖关系[17]。Mogren[18]提出了具有GAN 的连续循环神经网络（C-RNN-GAN,continuous recurrent neural network with adversarial training）模型，是最早利用RNN 的GAN 生成连续序列数据的例子。该模型的生成器是一个LSTM 网络，鉴别器是一个双向的LSTM 网络，通过时间反向传播和正则化的小批量随机梯度下降，训练生成器和鉴别器的网络参数。

Esteban 等[19]提出了循环条件生成对抗网络（RCGAN,recurrent conditional generative adversarial network）模型。它的生成器和鉴别器都采用RNN，和C-RNN-GAN 不同的是，RCGAN 的生成器和鉴别器的输入需要加入附加条件来控制结果。此模型的损失函数采用二分类交叉熵（BCE,binary cross entropy），能够描述真实数据与合成数据之间的关系。RCGAN 模型是很多后续工作的模型参照。

Yoon 等[20]提出了一种时间序列生成对抗网络（TimeGAN,time-series generative adversarial network），并利用了传统的无监督GAN 训练方法和更可控的监督学习方法。具体而言，该网络能够生成具有时间动态特性的时间序列。TimeGAN 由嵌入网络、恢复网络、生成器和鉴别器4 个网络组件组成。自动编码网络（前2 个网络）与生成对抗网络（后2 个网络）联合训练，嵌入网络和恢复网络负责数据到隐式特征的转换，生成对抗网络在此空间内学习数据的潜在有效特征。

TimeGAN 主要用于生成短时间序列，因为长时间序列会大大增加生成建模的维数要求，导致复杂度过高。为了解决这个问题，Ni 等[21]提出一个名为Signature Wasserstein-1的度量并将其作为鉴别器的评价结果，同时提出了一种新的生成器，称为条件自回归前馈神经网络，它抓住了时间序列的自回归性质，加快了训练的速度，整个模型被称为SigWGAN（signature Wasserstein generative adversarial network）。

尽管已有工作能够实现多种类型时间序列的生成，但是上述模型也存在不足。一是原始GAN面临梯度消失的问题。在训练初期，生成器的合成数据与真实数据相差很大，鉴别器可以利用高置信度区分二者，但损失函数无法为生成器提供足够大的梯度，最终导致梯度消失。二是时间序列的特征提取和利用的问题。时间序列数据的特征有多方面，涉及周期性、相关性和频域的特征等。单一鉴别器能够完成对时间序列特征的鉴别，但是不具有针对性。

对于上述2 个代表性问题，本文设计了多鉴别器的模型。多鉴别器针对时间序列的不同特征进行针对性的鉴别，在初期训练中合成数据不会因为某一项特征不明显而直接导致梯度消失，同时也有助于提高生成器合成数据的质量。

2 多鉴别器生成对抗网络模型

本文以GAN 和RNN 为基础提出了MDGAN的模型。此模型主要由3 个部分组成，分别是数据处理、生成器和多鉴别器。多鉴别器GAN 结构如图1 所示。在整个模型中，生成器输出的合成数据为G(ZN)，其中ZN为输入的随机噪声。合成数据经过数据处理得到T(G(ZN))，真实时间序列XN经过数据处理得到T(XN)。处理后的数据通过多鉴别器进行真/假判定。最后，通过计算鉴别器的损失函数D loss 和生成器的损失函数G loss 分别更新鉴别器和生成器的网络参数。

图1 多鉴别器GAN 结构

下面，分别介绍模型的组成部分、模型训练中的损失函数和训练方法。

2.1 数据处理

数据处理的目的是得到数据的不同特征。本文以真实时间序列的处理过程为例，介绍数据处理的流程。数据处理流程如图2 所示。

图2 数据处理流程

真实时间序列XN是一段长度为N的序列。序列可以描述为

在数据处理的过程中，时间序列XN通过傅里叶变换得到频域数据F(XN)；通过对时域和频域数据的处理和拼接得到时频域数据TF(XN)；通过自相关处理得到自相关函数ACF(XN)。处理后的数据按顺序组合为T(XN)，排序方式为

T(XN)是将3 种数据组合在一起。接下来，对式(3)中的3 个部分分别进行介绍。

2.1.1 傅里叶变换

离散傅里叶变换（DFT,discrete Fourier transform）是信号分析最基本的方法[22]。该方法将时间序列从时间域变换到频率域，分析时间序列的频域结构与变化规律。本文对长度为N的时间序列XN做M点的离散傅里叶变换。M的取值是2的整数幂，且大于或等于时间序列的长度N。XN的表达式为

其中，x(n)是时间序列XN中的第n个值，X(k)是傅里叶变换后的值。在模型中使用的方法是快速傅里叶变化（FFT,fast Fourier transform）。

离散傅立叶变换后的数据是一组复数，其中一半数据和另一半数据是共轭关系。本文只取一半数据F(XN)。F(XN)的表达式为

2.1.2 时域与频域拼接处理

傅里叶变换只反映数据在频域的特征，为了将时域和频域的特征联系在一起，常用短时傅里叶变换方法，其实质是加窗的傅里叶变换。这种方法是一种数据变形处理。但是本文希望从原始数据出发，得到一种同时包含时域数据和频域数据的形式。所以本文采取时域数据和频域数据拼接的方法分析特征。

具体的拼接方法是首先对频域数据取模后得到|F(XN)|。取模是一种对复数进行计算的方法，假设复数z=a+bi，复数模值计算为

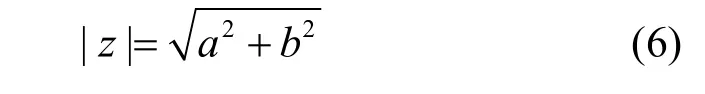
F(XN)中的每一个值都是复数，对每一个值取模之后，本文可以得到|F(XN)|的表达式，即

然后，将频域数据的模值|F(XN)|和时域数据XN拼接的数据看作一组同时包含时域和频域特征的数据，定义为时频域数据TF(XN)。时频域数据TF(XN)的表达式为

2.1.3 自相关函数处理

自相关函数（ACF,autocorrelation function）在信号处理中经常用来分析数据并描述数据的相似性[23]。通过使用自相关函数对时间序列进行处理，进一步对数据在时域上的特征进行分析。本文将自相关函数定义为ACF(XN)。离散序列的自相关函数的表达式为

其中，x(n)表示时间序列XN中的第n个值，m表示时间间隔。

2.2 生成器和鉴别器的网络结构

生成器和鉴别器的网络由LSTM 网络构成。LSTM 网络是RNN 的变体，一般用于与时间序列相关的任务，它由一系列结构相同的神经元构成，该神经元在每个时间步中重复使用。LSTM 的神经元内部有一个记忆状态，在处理序列数据时，输入不仅有序列数据，还有上一个时刻的记忆状态，并向下一个时刻输出当前的记忆状态。因此LSTM 网络是处理时间序列常用的网络。

2.2.1 生成器网络

生成器的网络结构主要由LSTM层和全连接层构成。生成器在每个时间步的输入获取不同的随机噪声向量。随机噪声向量由标准正态分布采样得到，并通过LSTM 网络进行计算。LSTM 网络的激活函数是tanh 函数。全连接层将LSTM 层的输出转换为指定的长度。生成器的网络结构如图3所示。

图3 生成器的网络结构

LSTM 网络的层数为2，隐藏层的神经单元个数为64。全连接层采用Linear 函数进行转换，并将每个时间步的全连接层的输出组合后得到合成数据。

2.2.2 鉴别器网络

鉴别器是对合成时间序列和真实时间序列的每个时间步的输出进行鉴别，最后取均值得到真/假的评价。鉴别器的网络结构如图4 所示。

图4 鉴别器的网络结构

Data 表示输入鉴别器网络的数据，是真实数据或合成数据以及它们的变体。鉴别器的网络结构和生成器的网络结构类似。鉴别器的全连接层使用Sigmoid 函数，将最后的输出转化为[0,1]区间的值。输出代表鉴别器对输入的评价。本文提出的模型包含多个鉴别器，不同的数据需要通过不同的鉴别器。

合成数据和真实数据的处理过程相同，本文以真实数据的鉴别过程为例说明多鉴别器如何对数据进行鉴别。多鉴别器的处理流程如图5 所示。

图5 多鉴别器的处理流程

每个鉴别器网络的输出y的取值范围为[0,1]，将4 个鉴别器的输出数值进行平均，定义最终结果大于或等于0.5 的是真实数据（评价为真），小于0.5 的是合成数据（评价为假）。因此，输出结果可表示为

经过数据处理的数据T(XN)在通过频域鉴别器、时频域鉴别器和自相关鉴别器时分别提取出与之相对应的数据。将不同鉴别器的评价结果进行平均得到最终结果。

2.3 模型训练

MDGAN 模型的训练分2 个部分介绍，第一部分介绍模型的损失函数，第二部分介绍模型的训练过程。

2.3.1 损失函数

MDGAN 模型的训练包括鉴别器和生成器2 个部分的训练。在训练中本文使用二分类交叉熵计算损失函数。BCE 的计算式为

鉴别器的目的是分辨出真实数据和合成数据。在训练中本文使用二分类交叉熵对鉴别器的预测和数据的标签进行计算。真实数据的标签为1，合成数据的标签为0。

越是优秀的鉴别器对真实时间序列的鉴别结果越接近1，对合成时间序列的鉴别结果越接近0。因此在鉴别器训练时，本文最小化数据通过鉴别器的结果与对应标签的二分类交叉熵。鉴别器的损失函数为

因为模型有多个鉴别器，需要分别计算结果。将计算结果代入式(12)中，然后利用式(12)对4 种鉴别器的网络参数进行更新。4 种鉴别器的计算结果分别为

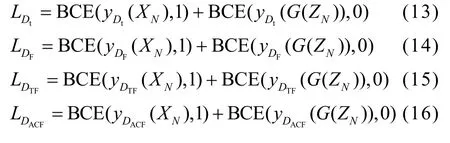
生成器的目的是随机噪声通过生成器生成与真实数据类似的合成数据。因此生成器生成的合成数据在通过鉴别器时，希望得到的评价是真实的。越是优秀的生成器生成的合成数据通过鉴别器的预测值越接近1。因此在生成器训练时，本文最小化合成数据通过鉴别器的结果与真实标签的二分类交叉熵。生成器的损失函数为

式(12)～式(17)中，Dt代表时域鉴别器，DF代表频域鉴别器，DTF代表时频域鉴别器，DACF代表自相关鉴别器，G代表生成器，yD代表鉴别器结果，XN代表真实时间序列，G(ZN)代表合成数据（1 代表真实，0 代表虚假）。

2.3.2 训练过程

在训练过程中，本文需要先对数据集进行预处理再进行训练。

数据集的预处理是先取出所有数据并进行归一化计算，然后将数据分为多个固定长度的序列进行随机组合。例如，把10 000 个数据按20 的固定大小分为500 组，然后将这500 组数据进行随机组合，目的是混合数据并使其类似于独立同分布。将预处理之后的真实时间序列分布定义为pr，随机噪声数据的分布pz是正态分布。

在鉴别器和生成器的训练过程中，先对鉴别器进行训练，更新鉴别器参数，同时固定生成器的参数；然后对生成器进行训练，更新生成器参数，同时固定鉴别器的参数。重复上述过程。训练中对参数更新的方法采用Adam 优化算法[24]。多鉴别器生成对抗网络生成样本算法如算法1 所示。

算法1多鉴别器生成对抗网络生成样本算法

输入批量值m，随机噪声z，真实样本x，学习率γ，鉴别器更新次数nd，Adam 超参β

输出生成器G，鉴别器D

初始化生成器参数θg，鉴别器参数θd

1) whileθghas not converged do

2) fort=0,1,…,nddo

3) 获取真实数据 (x(1),…,x(m))～pr

4) 获取噪声数据 (z(1),…,z(m))～pz

6)endfor

7)获取噪声数据（z(1),…,z(m)）～pz

9) end while

10) returnG，D

3 实验结果分析

本节介绍实验使用的数据集和评价指标，通过评价指标对实验结果进行分析。在实验中，为了更好地评估模型的性能，本文进行了横向和纵向对比。纵向对比中使用MDGAN 与频域鉴别器GAN、自相关鉴别器GAN、时频域鉴别器GAN 进行比较。横向比较中使用3 种具有代表性的时间序列生成模型与MDGAN 进行比较，分别是RCGAN[19]、TimeGAN[20]和SigCWGAN[21]。

3.1 数据集

本文实验使用的数据集是地磁数据集和牛津大学金融学院股票数据集中的标准普尔500 指数数据集。

地磁数据集共包含11 500 条数据。该数据是由手机自带的地磁传感器收集的一段5 min 内随手机姿态变化的地磁数据。地磁数据集经常用来分析和预测实验者使用时手机的不同姿态。

标准普尔500 指数数据集是牛津大学金融学院收集的股票数据，包括2000—2021 年的标准普尔500 指数数据集，共有5 515 条数据。每条数据包括每天的开盘价格、收盘价格和价格波动率。股票数据集经常用来分析和预测股票的趋势。

3.2 性能评估

实验中采取3 种常用的评估方法，分别是loss函数收敛性、主成分分析法（PCA,principal component analysis）和误差分析，分别从定性和定量的角度说明MDGAN 的性能。

1) loss 函数收敛性。loss 函数的收敛性主要用于评价模型的训练速度。

2) 主成分分析法。主成分分析法用于评价合成数据的分布情况，是最常用的线性降维方法。它的目标是通过某种线性投影将高维的数据映射到低维的空间中，并期望在所投影的维度上数据的信息量最大，实现使用较少的数据维度保留较多的原数据点特性。

3) 误差分析。误差分析评价合成数据的准确性。本文对合成时间序列和真实时间序列进行误差分析，并使用均方误差（MSE,mean square error）、均方根误差（RMSE,root mean squared error）、平均绝对误差（MAE,mean absolute error）和平均绝对误差百分比（MAPE,mean absolute percentage error）这4 种误差评价指标。

3.3 纵向对比结果

在纵向对比中，本文只使用地磁数据集对模型进行比较。纵向比较的模型有MDGAN、频域鉴别器GAN、时频域鉴别器GAN 和自相关鉴别器GAN。MDGAN 中包含所有数据处理过程和对应的鉴别器，其他模型只包含一种数据处理过程和对应的鉴别器。纵向对比是为了说明多鉴别器GAN 的合成数据比只包含一种鉴别器的GAN 模型的合成数据更加接近真实数据。

因为数据处理方式不同，4 种模型在loss 函数收敛性和主成分分析上的对比意义不是很重要，所以在纵向对比中本文只使用误差分析对模型合成数据的准确性进行分析。误差对比如表1 所示。

表1 模型误差对比

从表1 可以看出，时频域鉴别器GAN 的误差大多略优于频域鉴别器GAN 和自相关鉴别器GAN 的误差。但是MDGAN 模型的误差明显优于另外3 种模型的误差。所以本文MDGAN 模型生成的合成数据更加准确。

3.4 横向对比结果

3.4.1 loss 函数收敛性分析

为了对比模型的loss 函数收敛性，本文使用地磁数据集对MDGAN、SigCWGAN、TimeGAN和RCGAN 这4 种模型进行训练，损失函数的变化如图6 所示。其中，Sig loss 表示SigCWGAN模型的损失函数。

图6 训练过程中损失函数的变化

由图6 可以看出，TimeGAN 和RCGAN 模型的loss 函数在1 000 次左右还没有趋于稳定，但是SigCWGAN 和MDGAN 模型的loss 函数在400 次左右已经趋于稳定。这是因为TimeGAN 和RCGAN采用单一鉴别器，在训练过程中这2 种模型会在生成器和鉴别器之间的博弈花费更多的时间，不如多鉴别器GAN 的训练效率高。MDGAN 拥有多个鉴别器，在与生成器的博弈过程中会更加准确地对序列进行评价，这样有利于生成器快速地获得数据特征。而SigCWGAN 将生成器和鉴别器的损失函数合为一个损失函数，因此会提高训练的速度。综上，本文所使用的MDGAN 在模型训练的收敛速度上要优于TimeGAN 和RCGAN，与SigCWGAN 不相上下。

3.4.2 主成分分析

为了直观地观察数据的分布，本文采用了主成分分析法将原始数据和合成数据的特征降维到二维平面，来观察数据之间的差异。

本文使用2 个数据集进行实验，对4 种模型进行评价。对比结果分别如图7 和图8 所示。合成数据覆盖部分越大，说明模型越优秀。对比2 个数据集在4 组模型中的实验可以看出，MDGAN 模型在2 个数据集训练得到的合成数据分布均优于TimeGAN、SigCWGAN 和RCGAN 的合成数据分布。因为MDGAN 模型采用多鉴别器对合成数据的多个特征进行鉴别，所以合成数据的分布更加接近真实数据的分布。

3.4.3 误差分析

从图7 和图8 中能直观看到合成数据的分布是接近真实数据数据分布的，但是不能客观地评价合成数据的好坏，因此本文对2 个数据集的合成数据进行误差分析，分别如表2 和表3 所示。其中，股票数据集在预处理阶段已进行归一化处理。

表2 地磁数据集不同模型误差对比

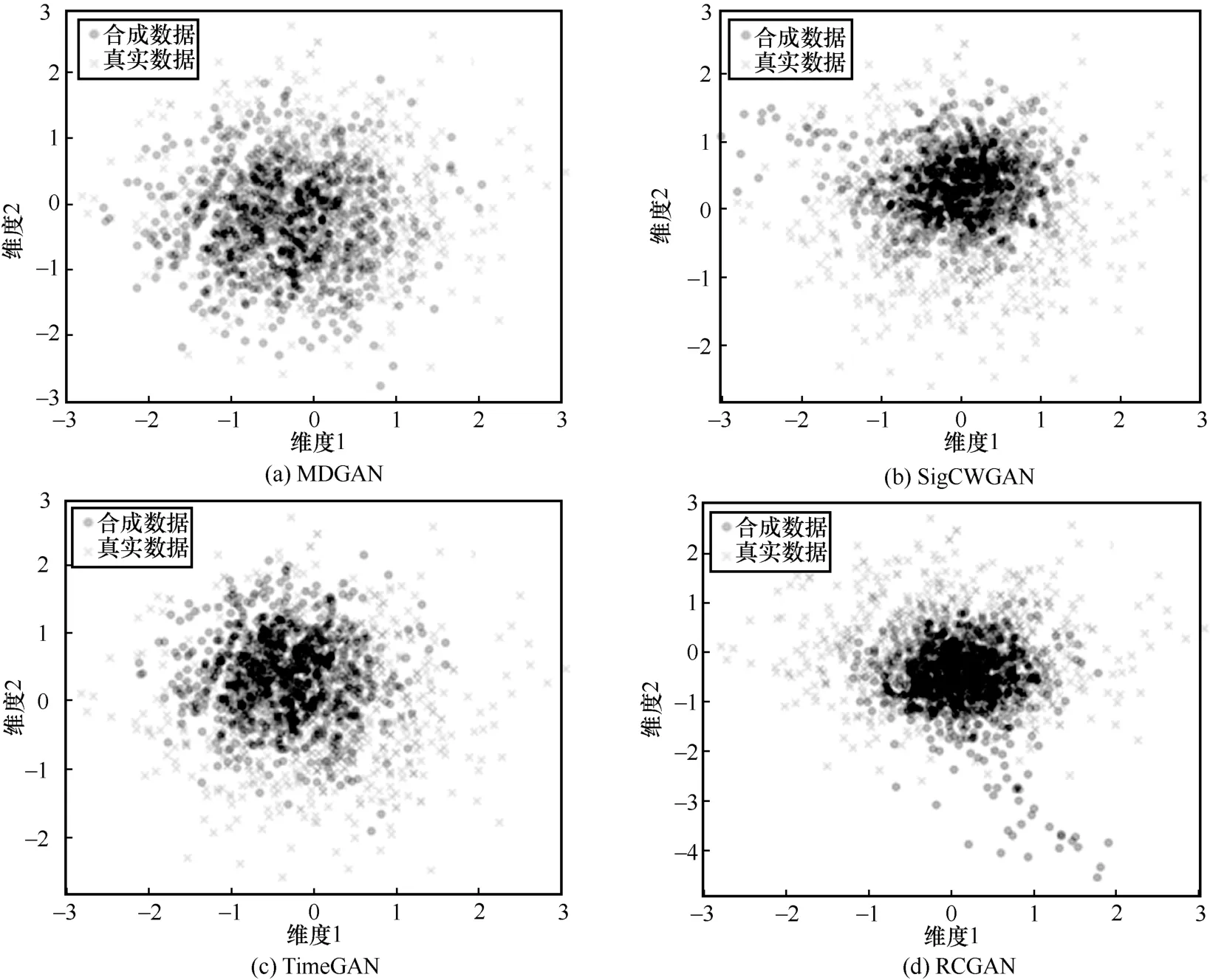
图7 地磁数据集PCA 可视化结果

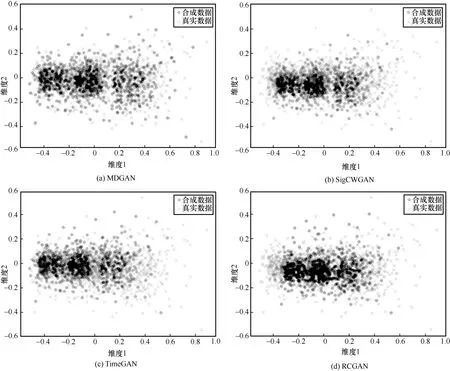
图8 股票数据集PCA 可视化结果

从表2 和表3 可以看出，MDGAN 的误差略低于 TimeGAN，但是明显低于 SigCWGAN 和RCGAN。这说明本文所提模型的准确性要高于其他3 种模型。

表3 股票数据集不同模型误差对比

3.4.4 总体分析

在loss函数收敛性方面，MDGAN与SigCWGAN不相上下，明显高于TimeGAN 和RCGAN。在主成分分析中，MDGAN 模型合成数据的分布最接近真实数据的分布。在误差分析中，MDGAN 的误差略低于TimeGAN，但是明显低于SigCWGAN 和RCGAN。

从模型的综合性能比较，本文所提MDGAN 要略优于 SigCWGAN 和 TimeGAN，明显高于RCGAN。

4 结束语

本文设计了基于生成对抗网络的多鉴别器时间序列生成模型，该模型采用4 种不同的鉴别器对合成数据进行鉴别，进而更好地识别时间序列的数据特征，使生成器能够快速合成高质量的数据。实验表明，对于地磁和股票这2 种不同类型的数据集，所提模型均能够合成出与真实数据近似度较高的数据，在模型收敛性、合成数据分布以及合成数据误差3 个方面都保持了良好的性能。

本文所设计的MDGAN 模型能够为一些需要大量时间序列数据集的用户提供一个获取数据的有效手段。尽管本文所提模型只通过2 种数据集进行了实验验证，但该模型的设计思路是可以借鉴并拓展的。在面对更加广泛的时间数据集时，可以采取针对性的特征鉴别，适当调整鉴别器的结构，使其达到复杂度和精度的最优折中。未来可进一步对特征提取的环节进行研究，使生成器输出的合成数据具有更强的可控性。