一种基于快速分解后向投影的条带SAR成像新方法

2015-10-13李浩林邢孟道

电子与信息学报 2015年8期

李浩林张磊邢孟道保铮

李浩林*张磊邢孟道保铮

(西安电子科技大学雷达信号处理国家重点实验室西安 710071)

快速分解后向投影(Fast Factorized Back-Projection, FFBP)最初用于超宽带SAR成像，并在聚束SAR信号处理领域取得了巨大的成功。然而，由于积分孔径和角域升采样的限制，FFBP算法难以直接用于条带SAR处理。为了提高FFBP算法在条带SAR处理的实用性，该文从积分孔径和角域波数带宽的角度出发，提出一种适用于条带SAR处理的重叠图像法。该方法极大地保留FFBP算法的运算效率，有效地避免因角域升采样带来数据量大的问题。最后，通过斜视条带SAR仿真实验验证了该方法的有效性。

合成孔径雷达；后向投影积分；快速分解后向投影；积分孔径；角波数带宽

1 引言

条带SAR在运动过程中保持天线波束指向的固定，通过波束连续扫过观测场景实现高效的遥感测绘[1]。典型的SAR成像方法包含频域算法和时域算法[2,3]。随着硬件技术的发展和使用需求的提高，SAR成像将不断面临严苛的成像环境，如高分辨[4]、宽测绘[5]和复杂航迹等[6,7]。一方面，严重的距离-方位耦合极易导致频域算法的测绘范围受限，甚至无法实现图像聚焦。另一方面，频域算法对理想的阵列流形(直线航迹和沿迹均匀采样)的要求在实际应用中难以满足。相比之下，时域算法不但不受非均匀的沿迹采样的影响[8]，还能实现图像的精确聚焦和宽幅测绘。

后向投影(Back-Projection, BP)是一种精确的时域算法，然而高的运算复杂度限制其在数据规模较大场合的应用。为此，一些能够加速BP积分的快速算法相继被提出，其中快速后向投影(Fast BP, FBP)[9]和快速分解后向投影(Fast Factorized BP, FFBP)[10]的运算复杂度分别为和。BP积分是时域算法的核心，它是一个能量连续积累的过程，要求所有待重建的像素点位于同一个积分区间，即积分孔径。以聚束SAR[11]为例，成像场景在合成孔径时间内始终被波束覆盖，即待重建的所有像素点对应同一个积分孔径，因此时域算法能够直接用于聚束SAR处理。对于条带SAR，成像场景中任意点目标不可能始终被波束覆盖，不同的像素点可能对应不同的积分孔径。如果在BP积分过程中引入积分孔径判断，并将当前孔径位置处的距离脉冲压缩回波数据投影至波束能够覆盖的像素点，BP算法和FBP算法是能够用于条带SAR处理的，但是将FFBP算法拓展至条带SAR仍是一个严峻的挑战。文献[12]提出了在后向投影过程中引入波束宽度限制的思路。由于未给出实施细节且仿真实验仅停留在对BP算法的改进层面，文献[12]的借鉴性有限。文献[13]明确地指出FFBP算法难以直接用于条带SAR的原因，提出了一种基于四叉树的加窗分解BP算法，区别于文献[10]提出的FFBP算法。

以实现FFBP算法在条带SAR中的应用为目标，本文首先回顾了FFBP算法的基本原理，介绍了FFBP算法直接用于条带SAR处理的问题，如积分孔径和角域升采样等。然后，以积分孔径和角域波数带宽的恢复为出发点，本文提出了利用图像重叠法，并从原理上清楚地解释了该方法适用于条带SAR成像的原因。图像重叠法无需角域升采样，极大地保留FFBP算法的运算效率优势，具有先聚束处理、后聚束-条带处理的特点。最后，通过仿真实验验证了图像重叠法的可行性和有效性。

2 FFBP算法概述

2.1基本原理

在初始阶段，FFBP算法将合成孔径划分为若干较短的子孔径，利用较少的脉冲便可以重建粗角分辨率的子孔径图像。子孔径的长度越短，FFBP算法的运算效率越高[10]；然而在实际处理时，子孔径的选取还需兼顾聚焦精度[14]。如图1所示，以为原点建立局部极坐标系，则第幅子孔径图像可以表示为

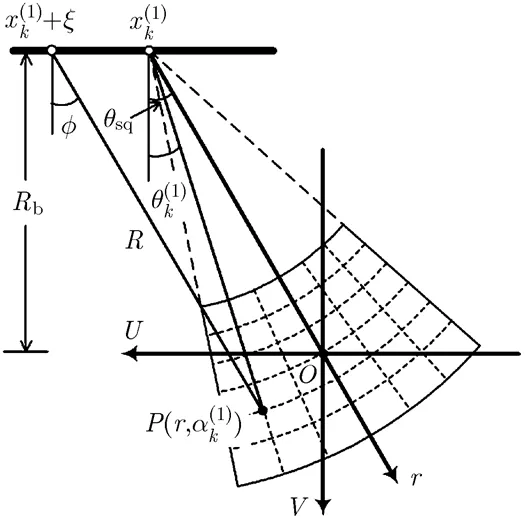
图1 第1阶段的第k个子孔径的局部极坐标网格

第2~阶段为递归融合阶段，先前阶段的子孔径图像通过相干相加得到当前阶段的子孔径图像，即

2.2直接用于条带SAR处理的问题

2.2.1积分孔径[10]明确的积分孔径(即积分限)是进行精确积分的一个重要环节。实际上，积分孔径与SAR系统的工作模式有关。对于聚束SAR，每个孔径位置对像素点的形成均有贡献。所有像素点对应同一个积分限，因此积分孔径为整个孔径。对于条带SAR，成像场景中的每个目标在合成孔径时间内不可能被天线波束一直照射。在进行BP积分时，不同的像素点可能对应不同的积分孔径。如果在进行BP积分时将距离压缩数据直接投影到整个成像网格，不但会引起波束宽度以外的像素点的能量的错误积累，影响成像质量，还会导致运算量的增加。因此，在进行条带SAR图像重建时，积分孔径还需针对不同的像素点做进一步确定。

2.2.2角域升采样当角域网格划分比较稀疏时，局部极坐标系具有低角域采样率的优势，这是FFBP算法能够利用SAR数据的冗余性来降低运算量的前提[10,16]。此外，局部极坐标系还能满足图像融合对波数谱无模糊、无混叠的要求，这是FFBP算法使用局部极坐标系的主要原因。然而，局部极坐标系既是联系孔径分解和递归融合的纽带，也是限制FFBP算法直接用于条带SAR处理的原因。

局部极坐标系之间的差异性导致不同的子孔径波数谱位于不同的波数空间，这给条带SAR角域采样需求的推导带来困难。全局极坐标系[15]是以条带SAR的整个孔径的中心为原点建立的极坐标系，因此全局极坐标系只有一个。当FFBP算法递归融合至一个子孔径时，局部极坐标系等价于全局极坐标系。如果使用全局极坐标系用于图像重建，所有子孔径图像及其波数谱位于同一波数空间。根据全局极坐标系下的波数谱，我们能够反演出局部极坐标系下的角域采样需求。

3 条带SAR处理

3.1积分孔径的判断

对于FFBP算法，初始阶段的子孔径图像质量直接决定了第2~G阶段的图像递归融合的精度。因此，在初始阶段的子孔径BP积分过程中需要引入积分孔径判断。根据SAR系统的工作模式的不同，积分孔径的计算需要做出相应的调整。由于条带SAR具有固定的波束指向，积分孔径与天线波束指向和天线方位波束宽度紧密相关。以图1中的点为例，假设点的极坐标为，其中。当天线到点的连线方向和视线方向的夹角不超过时，天线波束能够照射到点，即

3.2角域波数带宽

聚束SAR的整个孔径对每个像素点的形成均有贡献，因此所有像素点对应同一个积分孔径，且积分孔径的长度满足。如2.2节所述，积分孔径的长度决定角域波数带宽的大小，这是聚束SAR角域波数带宽等于的原因。对于条带SAR，固定的天线波束指向使得场景中的任一点目标无法一直被天线波束照射，因此每个像素点的积分孔径长度均不超过合成孔径长度，即。即使条带SAR包含多个合成孔径，每个像素点的角域波数带宽等于，且不超过。至此，我们发现了条带SAR和聚束SAR的共同点：积分孔径的长度决定角域波数带宽的大小。

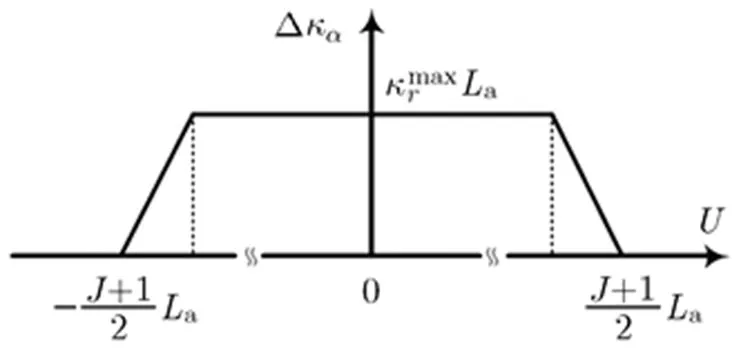
图2 全孔径下角域波数带宽

为了利用局部极坐标系的角域带宽优势和避免角域升采样，本文限制FFBP算法每次只针对一个合成孔径进行处理，即局部的聚束处理。对于一个完整的合成孔径来说，波束扫过的最大场景宽度为合成孔径长度的2倍，如图3所示。像素点的方位坐标越接近零，积分孔径的长度越接近；像素点的方位坐标越接近,越接近零，即

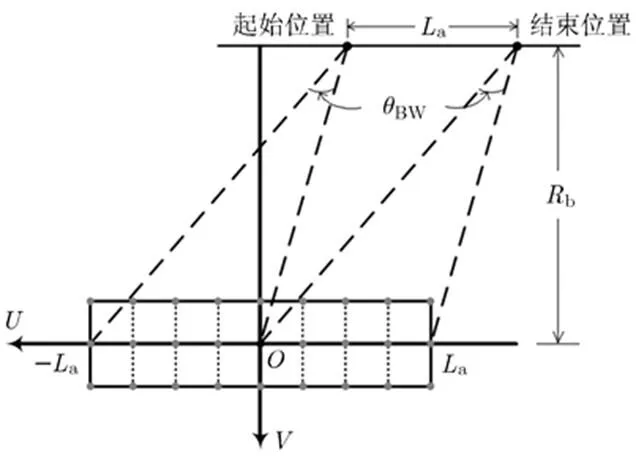
图3 合成孔径长度为La、成像网格宽度为2La时的几何构型

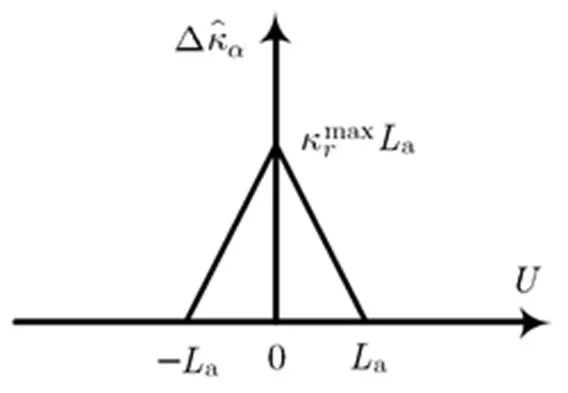
图4 合成孔径图像的角域波数带宽

3.3 重叠图像法

在3.2节的启发下，我们通过数学推导发现一种恢复像素点的真实积分孔径的方法，即

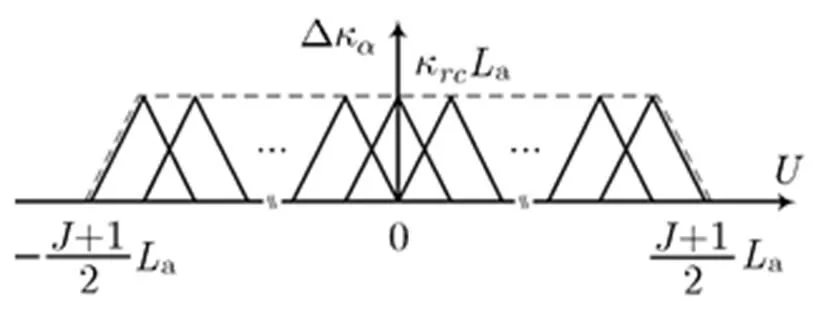
图5 (为奇数)个合成孔径恢复的真实积分孔径示意图

图6 重叠图像法的成像构型

4 仿真实验

下面开展一个近场、高分辨、超宽带斜视条带SAR仿真实验，详细参数如表1所示。如图7所示，该成像几何构型包含3个完整的合成孔径。每个合成孔径的长度为，包含的脉冲数为1024。考虑到条带SAR的工作特点，天线扫过的场景的方位宽度为。在斜平面上建立最终输出图像网格，成像网格的像素点数为1024×4096(距离×方位)，距离像素间隔为0.087 m，方位像素间隔为0.1 m。在该实验中，能够实现像素点完全聚焦的区间为[-102.4,102.4] m。我们将能够完全聚焦的像素用圆点表示，将不能够完全聚焦的像素点用五角星表示，其中点的坐标为(102.4,-40) m。

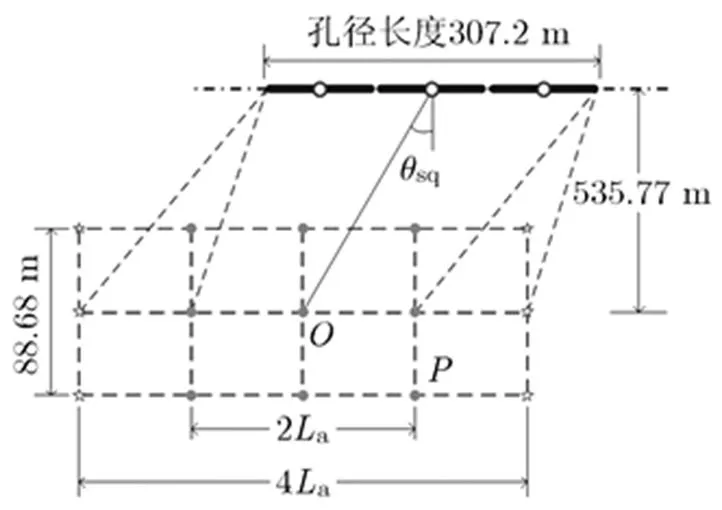
图7 仿真几何及点目标分布

表1仿真参数

为了清楚地展示重叠图像法的特点，我们特意在成像场景中设置了子母“LIHFE”点阵，并使用表1中的参数进行回波数据仿真。使用FFBP算法对每个合成孔径进行处理，共得到3幅图像，如图8(a), 8(b)和图8(c)所示。每幅图像均位于局部直角坐标系，其方位成像范围为[-102.4,102.4] m，且相邻两幅图像存在相同的成像区域。将3幅位于局部直角坐标的图像映射到最终输出图像网格，从而形成相邻合成孔径图像的重叠。然后通过相干相加得到最终输出图像，如图8(e)所示。以字母“H”为例，由于构成该字母的像素点的积分孔径在这3个合成孔径下均不足，因此该字母在图8(a), 8(b)和图8(c)均得不到完全聚焦。然而，当前图像中积分孔径不足的像素点可由相邻图像的同一位置的像素点进行补偿。在图8(a), 8(b)和图8(c)共同作用的情况下，字母“H”最终在图8(e)中实现完全聚焦。同理，字母“I”和“F”也能得到完全聚焦，图8(d)为点成像结果放大图。然而，位于[-204.8, -102.4) m和(102.4,-204.8] m区间的像素点的积分孔径不足，因此字母“L”和“E”均无法得到完全聚焦。如果初始阶段的BP积分过程中不引入积分孔径判断，成像结果如图8(f)所示。虽然设置点目标能够得到良好聚焦，但是在图8(f)中还存在许多阴影。这些阴影可以理解为错误的BP积分引起的杂波，其能量水平在-30~-40 dB。因此，这些杂波一定程度上破坏了重建图像的真实性和降低了图像的信杂比，不利于图像中微弱目标的检测。

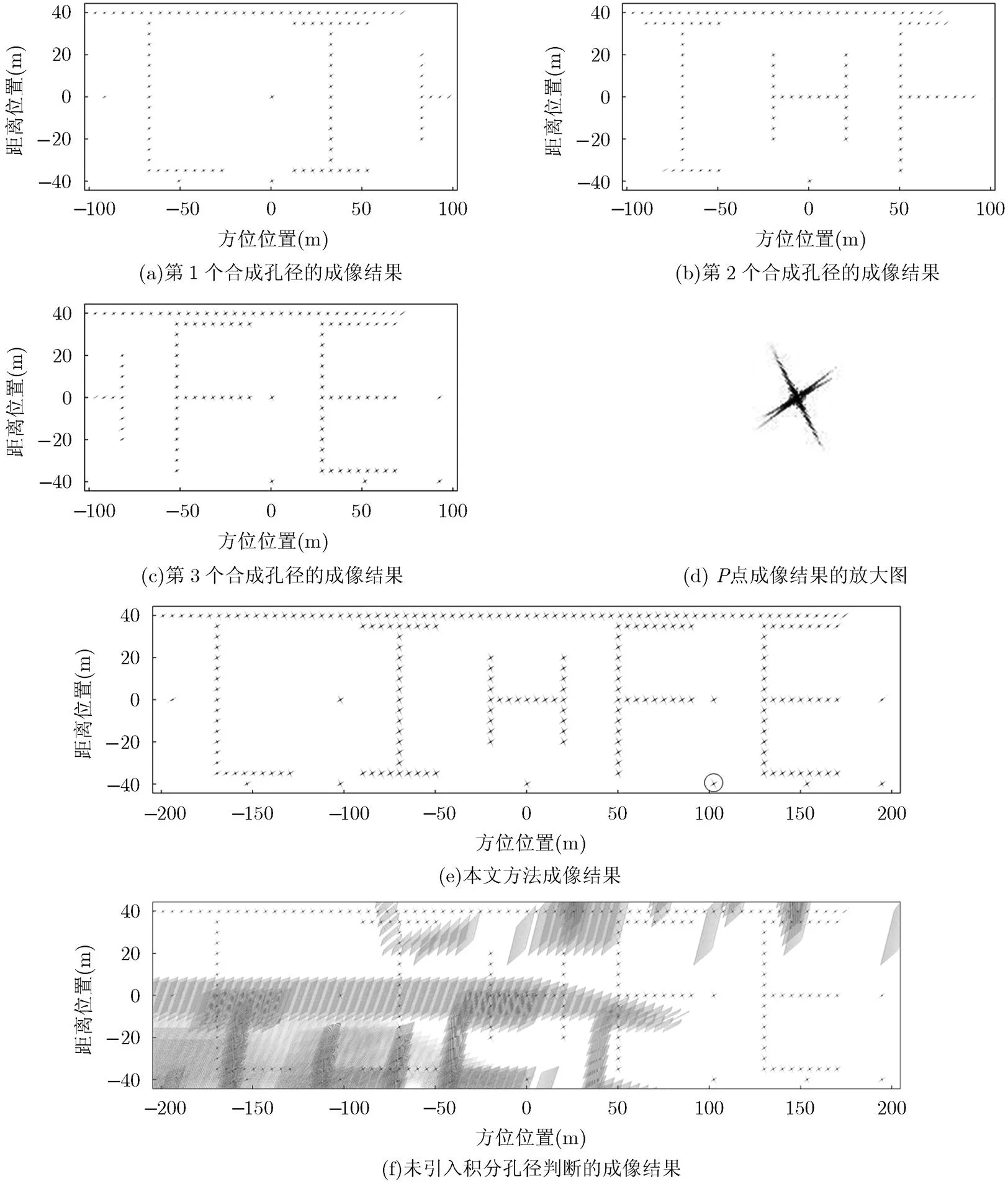
图8 合成孔径及整个孔径的SAR成像结果

5 结束语

本文指出了FFBP算法直接用于条带SAR存在的问题。除了积分孔径之外，局部极坐标系的角域升采样处理将给FFBP算法带来不必要的运算负担。在清楚了解局部极坐标系的特点后，我们着眼于FFBP算法在条带SAR处理中实用化的研究。以积分孔径和角域波数带宽作为出发点，本文提出了重叠图像法。该方法在初始阶段的后向投影过程中引入积分孔径判断，通过相邻合成孔径图像的相互叠加恢复各像素点应有的角域波数带宽，从而实现条带SAR处理。该方法不但继承了FFBP算法在运算效率和运动补偿方面的优势，而且避免了数据升采样问题。

参考文献

[1] Cumming I G and Wong F H. Digital Signal Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Boston, MA: Artech House, 2005: 5-7.

[2] Shippey G, Banks S, and Pihl J. SAS image reconstruction using fast polar back projection: comparisons with fast factored back projection and Fourier-domain imaging[C]. IEEE Oceans 2005-Europe, Brest, France, 2005: 96-101.

[3] Jakowatz C V and Doren N. Comparison of polar formatting and back-projection algorithms for spotlight-mode SAR image formation[J]., 2006, Vol. 6237: 62370H-1- 62370H-7.

[4] 胡建民, 王岩飞, 李和平. 基于回波数据的超高分辨率SAR通道相位误差估计与补偿[J]. 电子与信息学报, 2012, 34(7): 1602-1608.

Hu Jian-min, Wang Yan-fei, and Li He-ping. Channel phase error estimation and compensation for ultra-high resolution SAR based on echo data[J].&, 2012, 34(7): 1602-1608.

[5] 吴明宇, 杨桃丽, 吴顺君, 等. 星载多通道高分辨率宽测绘带SAR系统运动目标检测方法[J]. 电子与信息学报, 2014, 36(2): 441-444.

Wu Ming-yu, Yang Tao-li, Wu Shun-jun,.. Ground moving target indication for spaceborne multi-channel high resolution wide swath SAR system[J].&, 2014, 36(2): 441-444.

[6] 冉金和, 张剑云, 武拥军. 机载并行双站大斜视SAR两步式成像算法[J]. 电子与信息学报, 2014, 36(5): 1036-1043.

Ran Jin-he, Zhang Jian-yun, and Wu Yong-jun. Two-step imaging algorithm for airborne parallel high squint SAR[J].&, 2014, 36(5): 1036-1043.

[7] 潘舟浩, 李道京, 刘波, 等. 基于BP 算法和时变基线的机载InSAR 数据处理方法研究[J]. 电子与信息学报, 2014, 36(7): 1585-1591.

Pan Zhou-hao, Li Dao-jing, Liu Bo,.. Processing of the airborne InSAR data based on the BP algorithm and the time-varying baseline[J].&, 2014, 36(7): 1585-1591.

[8] Gorham L A, Majumder U K, Buxa P.. Implementation and analysis of a fast backprojection algorithm[J]., 2006, Vol. 6237: 62370G-1-62370G-8.

[9] Yegulalp A F. Fast backprojection algorithm radar for synthetic aperture radar[C]. Proceedings of IEEE Radar Conference, Waltham, MA, USA, 1999: 60-65.

[10] Ulander L M H, Hellsten H, and Stenström G. Synthetic-aperture radar processing using fast factorized back-projection[J]., 2003, 39(3): 760-776.

[11] Carrara W G, Goodman R S, and Majewski R M. Spotlight Synthetic Aperture Radar: Signal Processing Algorithm[M]. Boston, MA: Artech House, 1995.

[12] Ulander L M H, Frölind P O, and Mursin D. Fast factorized backprojection algorithm for processing microwave SAR data[C]. Proceedings of 6th European Conference on Synthetic Aperture Radar, Dresden, Germany, 2006: 577-580.

[13] Moon K and Long D G. A new factorized backprojection algorithm for stripmap synthetic aperture radar[J]., 2013, 4(1): 42-56.

[14] Frölind P O and Ulander L M H. Evaluation of angular interpolation kernels in fast back-projection SAR processing[J].,, 2006, 153(3): 243-249.

[15] Zhang Lei, Li Hao-lin, and Qiao Zhi-jun. A fast BP algorithm with wavenumber spectrum fusion for high-resolution spotlight SAR imaging[J]., 2014, 11(9): 1460-1464.

[16] 李浩林, 张磊, 杨磊. 一种改进的快速分解后向投影SAR成像算法[J]. 电子与信息学报, 2013, 35(6): 1435-1441.

Li Hao-lin, Zhang Lei, and Yang Lei. A novel fast factorized back-projection algorithm for synthetic aperture radar imaging[J].&, 2013, 35(6): 1435-1441.

Innovative Strategy for Stripmap SAR Imaging Using Fast Factorized Back-projection

Li Hao-lin Zhang Lei Xing Meng-dao Bao Zheng

(,,’710071,)

Fast Factorized Back-Projection (FFBP) is originally developed for Ultra-WideBand (UWB) Synthetic Aperture Radar (SAR), and it shows great success for spotlight SAR signal processing. However, its implementation is not straightforward for stripmap SAR due to the limitation of integration aperture and angular upsampling. To investigate the applicability of FFBP to stripmap SAR, this paper describes a reasonable implementation of overlapped-image method based on integration aperture and angular wavenumber bandwidth. This approach retains high efficiency of the original FFBP. Finally, the simulated squinted SAR data are utilized to verify the effectiveness of the proposed method.

SAR; Back-Projection (BP) integration; Fast Factorized Back-Projection (FFBP); Integration aperture; Angular wavenumber bandwidth

TN957.52

1009-5896(2015)08-1808-06

10.11999/JEIT141633

李浩林 lihaolin322@163.com

2014-12-25收到，2015-03-23改回，2015-06-09网络优先出版

国家自然科学基金(61301280)资助课题

李浩林：男，1987年生，博士，研究方向为SAR高分辨成像和运动补偿等.

张磊：男，1984年生，讲师，研究方向为SAR, ISAR高分辨成像与运动补偿等.

邢孟道：男，1975年生，教授，博士生导师，研究方向为雷达成像和目标识别等.

保铮：男，1927年生，教授，中国科学院院士，研究方向为SAR成像和目标识别等.