关于CE－投射模及其投射维数

谢国根

(铜陵学院数学与计算机学院，安徽铜陵244000)



关于CE－投射模及其投射维数

谢国根

(铜陵学院数学与计算机学院，安徽铜陵244000)

摘要:利用投射模的研究方法构造出了CE－内射模的对偶模类CE－投射模，刻画了CE－投射模及其CE－投射维数的一些性质;结论如下:假如F:RM→SM为模范畴的等价函子，G是F的逆函子，则M为R－CE－投射模当且仅当F(RM)为S－CE－投射模; RM在环R上的CE－投射维数与SF(RM)在环上的CE－投射维数是相等的，也即l．CEpd(RM) = l．CEpd(SF(RM) )．

关键词:CE－投射模; CE－投射维数，模范畴等价

1基础知识

投射模作为模论中最重要的一类模，极大地充实了代数学和同调代数．文献［1－6］对投射模进行了广泛而又深入的研究，此处在其基础上通过构造CE－投射模对投射模进行了推广．

此处参考文献［1］中的模范畴等价函子，并利用文献［2］中性质P:设R与S为等价环，F:RM→SM为模范畴等价函子，若模范畴某种性质P满足模M在R环上具有的性质P当且仅当F( M)在环S中也具有性质P，则称性质P为函子F的范畴等价性质．例如，性质P可以为单模、半单模、有限表现模等．令RX= { MRM M 满足性质P}．SX={ MSM M满足性质P}，利用上述性质P，进一步构造CE－投射模和CE－投射维数，并得到相关的等价结论．

环R与环S都是有单位元的结合环，且模均为酉模．

显然，投射模一定是CE－投射模．

定理1设R为环，对任意的左R－模M，下列结论等价:

1)左R－模M为CE－投射模;

4)假设F:RM→SM为模范畴等价函子，函子G为F逆函子，则F(RM)是环S上的左S－CE－投射模．

由定理1的1)可得Ext1R( M，K) = 0，所以π是满同态，即2)的结论成立．

由于左R－模A为内射模，可得Ext1R( M，A) = 0，又由条件可知π为满同态，所以Ext1R( M，K) = 0，由CE－投射模定义可知M为CE－投射模．

由1)知Ext1R( M，K) = 0，所以结论3)成立．

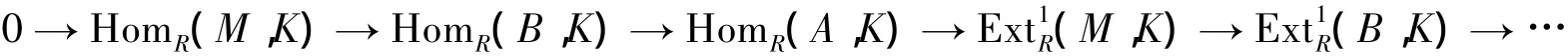
定理2对任意左R－模正合列0→M1→M→M2→0，下列结论成立:

1)若左R－模M1，M2为CE－射投模，则模M也为CE－投射模;

证明1)对左R－模正合列0→M1→M→M2→0，使用长正合列定理可得

根据模M1，M2为CE－投射模可知( M1，K) = 0，Ext1R( M2，K) = 0，则( K，M) = 0，故根据CE－投射模定义可得模M是CE－投射模．

2投射维数

因为投射模一定是CE－投射模，由文献［7］可知，投射模一定有投射分解，故CE－投射模有CE－投射分解，并且可类似定义CE－投射模的投射维数．记CE－投射模RM的投射维数为l．CEpd(RM)．

定理3设F:RM→SM为模范畴的等价函子，且函子G是函子F的逆函子，则RM在R环上的CE－投射维数和SF(RM)在S环上的CE－投射维数相等，即l．CEpd(RM) = l．CEpd(SF(RM) )．

证明设l．CEpd(RM) = n＜(其中Pi均为CE－投射模，i=1，2，3，…，n)，则对一切的左R－模M有形如正合列

的CE－投射分解，用函子F作用上述正合列，可得下列正合列:

假设l．CEpd(RM) =，显然l．CEpd(SF(RM) )≤l．CEpd(RM)总是成立的，综上，l．CEpd(SF(RM) )≤l．CEpd(RM)成立．

反之，如果l．CEpd(SF(RM) )≤n＜，由上述证明可得

又由于GF(RM)RM，即l．CEpd(RM)≤l．CEpd(SF(RM) )．

假设l．CEpd(SF(RM) ) =，则显然l．CEpd(RM)≤l．CEpd(SF (RM) )成立，综上，l．CEpd(RM)≤l．CEpd(SF(RM) )成立．

所以l．CEpd(RM) = l．CEpd(SF(RM) )．证毕．

参考文献:

［1］ANDERSON F W，FULLER K R．Rings and Categories of Modules［M］．Springer-Verlag，Berlin，1974

［2］谢国根，葛茂荣．关于CE-内射模［J］．阜阳师范学院学报，2011，89( 3) : 18-20

［3］黄影．FP-投射模［J］．吉林师范大学学报: 2007，39( 1) : 46-48

［4］唐义立，葛茂荣．FG平坦模［J］．重庆工商大学学报:自然科学版，2012，29( 4) : 20-23

［5］朱晓胜．正则环的同调维数［J］．南京大学学报:数学半年刊，1994，11( 2) : 226-232

［6］朱占敏．广义FP-内射模，广义平坦模与某些环［J］．数学理论与应用，2002，22( 3) : 40-46

On CE-projective Modules and CE-projective Dimension

XIE Guo-gen

( College of mathematics and computer，Tongling University，Tongling 244000，China)

Abstract:Making use of the research on projective module，this paper constructs CE-projective modules，the dual modules of CE-injective modules，and gives some properties of CE-projective modules and CE- projective dimension．The results are as follow: Suppose an equivalent of modules categories functor F:RM→SM，and G is inverse functor of F，( 1) M is CE-projective modules，if and only if F(RM) is CE-projective modules; ( 2) CE-projective dimension of M on ring R and CE-projective dimension F(RM) on ring S are equal，l．CEpd(RM) = l．CEpd(SF(RM) )

Key words:CE-projective modules; CE-projective dimension; equivalent of modules categories

作者简介:谢国根( 1985-)，男，江西抚州人，硕士，从事环论及代数表示论研究．

收稿日期:2014－06－23;修回日期: 2014－10－10．

doi:10．16055/j．issn．1672－058X．2015．0005．011

中图分类号:O153．3

文献标志码:A

文章编号:1672－058X( 2015) 05－0037－03